上海市南模中学2020年4月高一数学月考试卷及答案(PDF版)
文档属性
| 名称 | 上海市南模中学2020年4月高一数学月考试卷及答案(PDF版) |  | |
| 格式 | zip | ||
| 文件大小 | 428.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 09:53:54 | ||
图片预览

文档简介
南模中学高一数学测验试卷
2020.04
填空题
函数y=√9-x2+1g(2cos2x-1)的定义域是
若sinx=,x∈(0,x),则x=
3.函数y=tan(2x-)的对称中心为
4.函数f(x)=1+sin2x-cos2x|的最小正周期是
5.已知 arcsinx< arcsin(1-x),则x的取值范围为
6.当x∈[z,3]时,函数y= arcsin(csx)的值域是
7.函数y=sim-)SF13)的单调减区间为
8.y= arcsinx+ arctan的值域是
9.函数f(x)=gx-cos2x的零点个数是
10.函数f(x)=Asin(ox+q)(A>0,>0)的图像如
图所示,则f(1)+f(2)+f(3)+…+f(2020)=
11.函数f(x)= sin(ox+)(>0,一(1)图像关于x=一对称;
(2)图像关于点(,0)对称;
(3)周期是r
(4)在[-,0]上是增函数;
以其中两个论断作为条件,余下论断为结论,写出你认为正确的一个命题:
a asb
12.定义一种运算a⑧b=
b a>b
令f(x)=(Cos2x+sinx)②,且x∈[0,],则
函数f(x--)的值域是
选择题
13.为了得到函数y=2036·x∈R的图像,只需把函数y=2sinx,r∈R的图像
上所有的点()
A.向右平移竺个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
C.向右平移竺个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变)
D.向左平移二个单位长度,再把所得各点的横坐标伸长到原来的一倍(纵坐标不变)
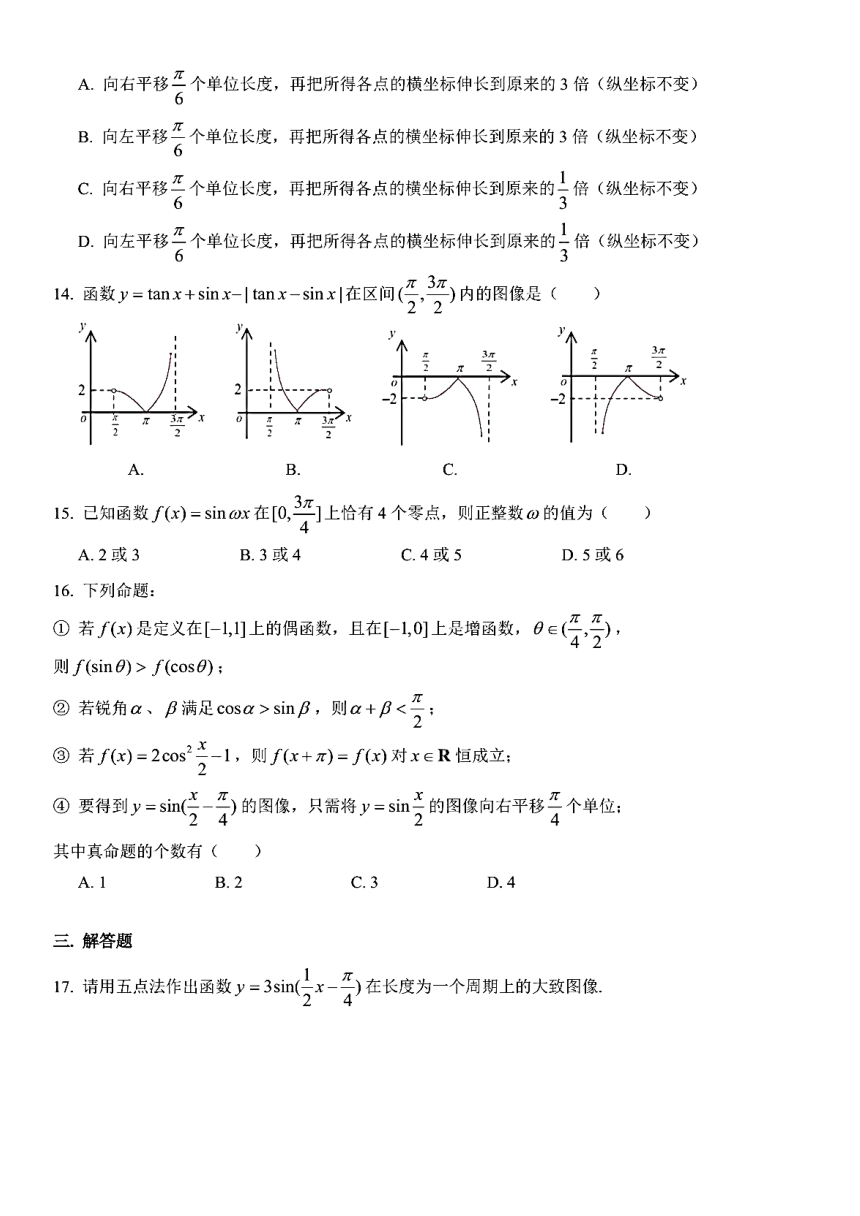
14.函数y=mx+ sinx-tanx-smx1在区间(,3z)内的图像是()
B
c
15.已知函数(x)=5max在[.32]上恰有4个零点,则正整数o的值为()
A.2或
B.3或4
C.4或5
D.5或6
16.下列命题
①若f(x)是定义在[-1,1上的偶函数,且在[-10上是增函数,∈(,)
则f(sin)>f(cos6);
②若锐角a、β满足csa>sinB,则a+β“2
③若f(x)=2cos2-1,则f(x+)=f(x)对x∈R恒成立
④要得到y=si(x-z
24)的图像,只需将y=in的图像向右平移个单位
其中真命题的个数有
B.2
C.3
4
三.解答题
1请用五点法作出函数y=3sim(x-在长度为一个周期上的大致图像
2020.04
填空题
函数y=√9-x2+1g(2cos2x-1)的定义域是
若sinx=,x∈(0,x),则x=
3.函数y=tan(2x-)的对称中心为
4.函数f(x)=1+sin2x-cos2x|的最小正周期是
5.已知 arcsinx< arcsin(1-x),则x的取值范围为
6.当x∈[z,3]时,函数y= arcsin(csx)的值域是
7.函数y=sim-)SF13)的单调减区间为
8.y= arcsinx+ arctan的值域是
9.函数f(x)=gx-cos2x的零点个数是
10.函数f(x)=Asin(ox+q)(A>0,>0)的图像如
图所示,则f(1)+f(2)+f(3)+…+f(2020)=
11.函数f(x)= sin(ox+)(>0,一
(2)图像关于点(,0)对称;
(3)周期是r
(4)在[-,0]上是增函数;
以其中两个论断作为条件,余下论断为结论,写出你认为正确的一个命题:
a asb
12.定义一种运算a⑧b=
b a>b
令f(x)=(Cos2x+sinx)②,且x∈[0,],则
函数f(x--)的值域是
选择题
13.为了得到函数y=2036·x∈R的图像,只需把函数y=2sinx,r∈R的图像
上所有的点()
A.向右平移竺个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
C.向右平移竺个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变)
D.向左平移二个单位长度,再把所得各点的横坐标伸长到原来的一倍(纵坐标不变)
14.函数y=mx+ sinx-tanx-smx1在区间(,3z)内的图像是()
B
c
15.已知函数(x)=5max在[.32]上恰有4个零点,则正整数o的值为()
A.2或
B.3或4
C.4或5
D.5或6
16.下列命题
①若f(x)是定义在[-1,1上的偶函数,且在[-10上是增函数,∈(,)
则f(sin)>f(cos6);
②若锐角a、β满足csa>sinB,则a+β“2
③若f(x)=2cos2-1,则f(x+)=f(x)对x∈R恒成立
④要得到y=si(x-z
24)的图像,只需将y=in的图像向右平移个单位
其中真命题的个数有
B.2
C.3
4
三.解答题
1请用五点法作出函数y=3sim(x-在长度为一个周期上的大致图像
同课章节目录
