2018-2019学年湖南省邵阳市邵东县八年级(下)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年湖南省邵阳市邵东县八年级(下)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 06:42:23 | ||
图片预览



文档简介
2018-2019学年湖南省邵阳市邵东县八年级(下)期中数学试卷
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.(3分)在一个直角三角形中,有一个锐角等于65°,则另一个锐角的度数是( )
A.115° B.125° C.25° D.35°
2.(3分)下列四组数据中,“不能”作为直角三角形的三边长的是( )
A.3,4,6 B.5,12,13 C.6,8,10 D.,,2
3.(3分)如图,Rt△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,AD=10,则点D到AB的距离是( )
A.8 B.5 C.6 D.4
4.(3分)如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PD=PE,则△APD与△APE全等的理由是( )
A.SAS B.AAA C.SSS D.HL
5.(3分)下列说法中,不正确的是( )
A.有三个角是直角的四边形是矩形
B.对角线相等的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.对角线互相垂直的平行四边形是菱形
6.(3分)下面哪个点到三角形三边的距离相等( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三角形内任意一点
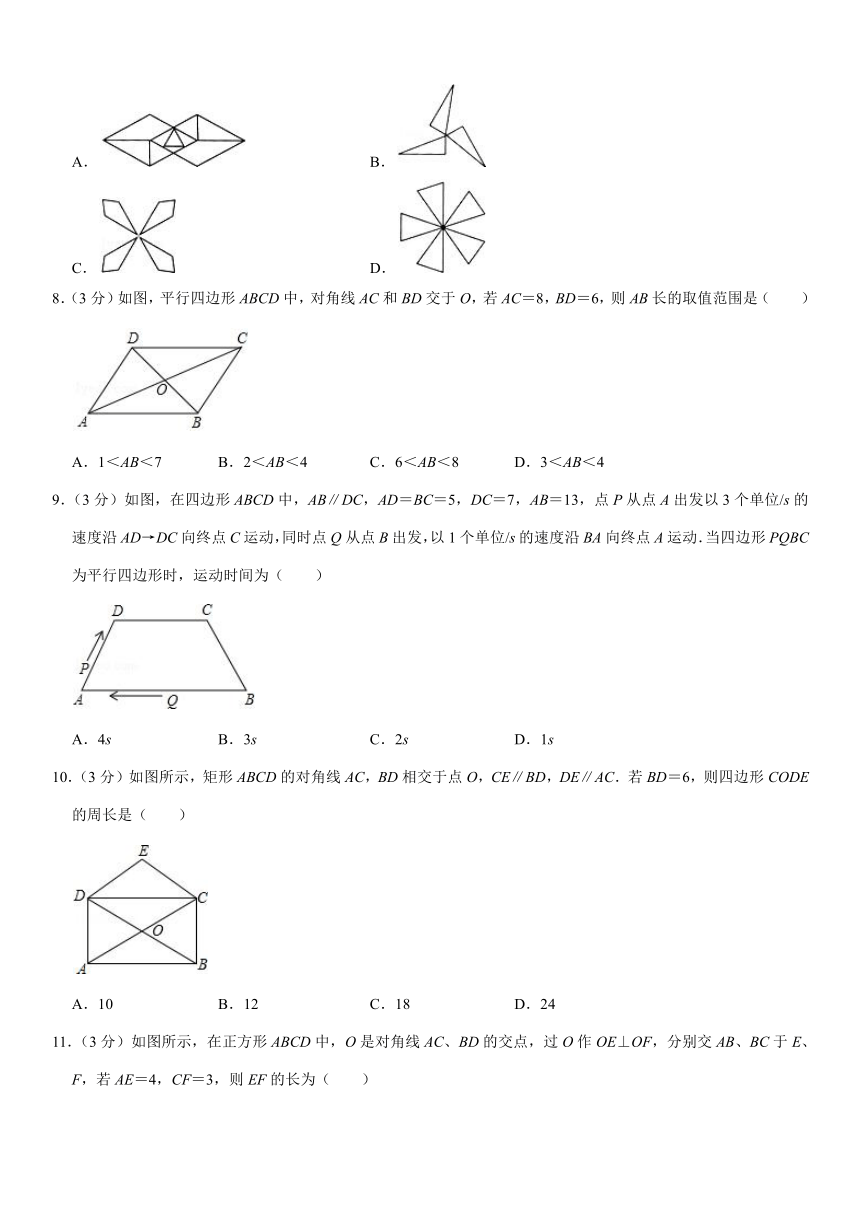
7.(3分)下列图形属于中心对称图形的是( )
A. B.
C. D.
8.(3分)如图,平行四边形ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则AB长的取值范围是( )
A.1<AB<7 B.2<AB<4 C.6<AB<8 D.3<AB<4
9.(3分)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
10.(3分)如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10 B.12 C.18 D.24
11.(3分)如图所示,在正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的长为( )
A.3 B.4 C.5 D.6
12.(3分)如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
A.cm2 B.cm2 C.cm2 D.()ncm2
二.填空题(共6小题)
13.(3分)一个多边形的每一个外角都等于36°,它是 边形.
14.(3分)如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 (写出一种情况即可).
15.(3分)如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
16.(3分)如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测到到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,塔的高度DE= m.
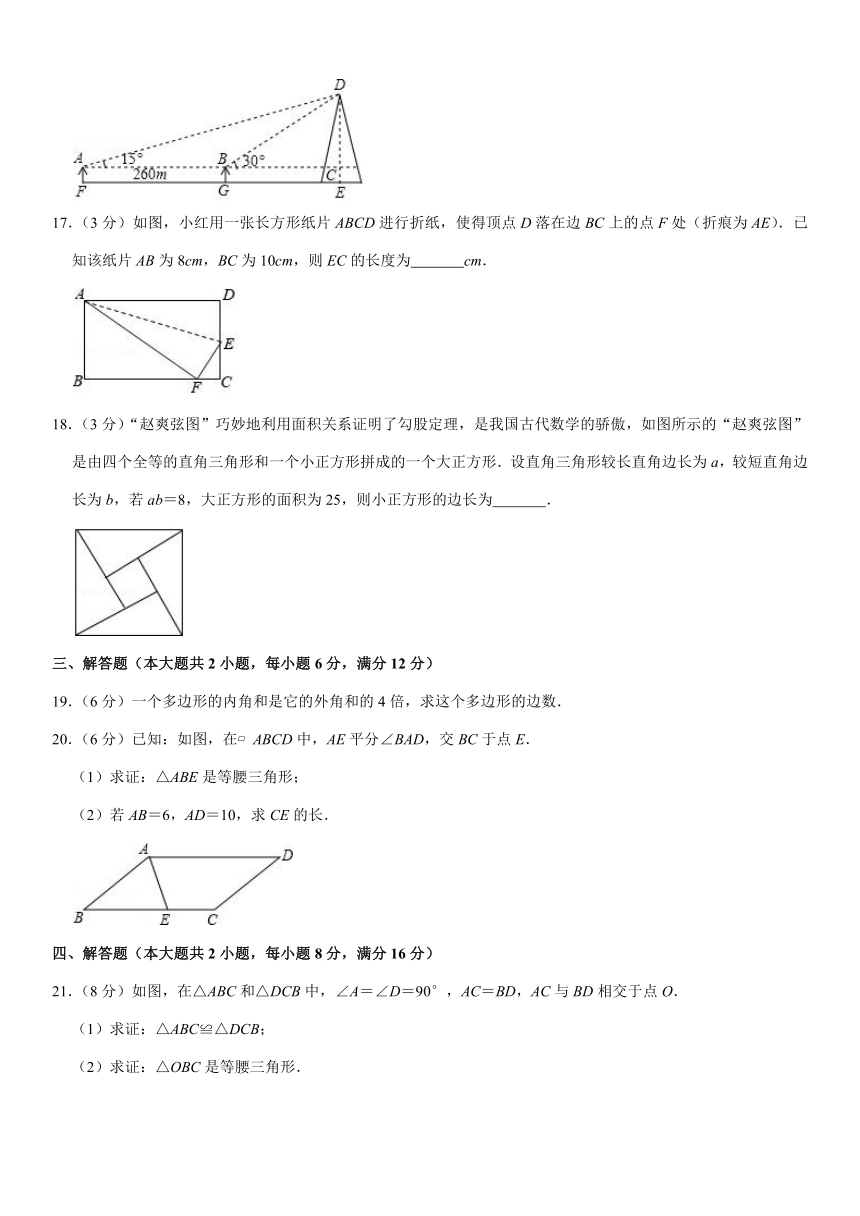
17.(3分)如图,小红用一张长方形纸片ABCD进行折纸,使得顶点D落在边BC上的点F处(折痕为AE).已知该纸片AB为8cm,BC为10cm,则EC的长度为 cm.
18.(3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为 .
三、解答题(本大题共2小题,每小题6分,满分12分)
19.(6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
20.(6分)已知:如图,在?ABCD中,AE平分∠BAD,交BC于点E.
(1)求证:△ABE是等腰三角形;
(2)若AB=6,AD=10,求CE的长.
四、解答题(本大题共2小题,每小题8分,满分16分)
21.(8分)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)求证:△OBC是等腰三角形.
22.(8分)如图,菱形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,已知AC=8cm,BD=6cm,
(1)求菱形ABCD的面积.
(2)求OE的长度.
五、解答题(本大题共2小题,每小题9分,满分18分)
23.(9分)如图,在?ABCD中,若点E、F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
24.(9分)如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由(提示:可作DG⊥AB于点G)
六、解答题(本大题共2小题,每小题10分,满分20分)
25.(10分)如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
26.(10分)已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②正方形对角线AE,DF相交于点O,连接OC.若OC为,求正方形ADEF的边长.
2018-2019学年湖南省邵阳市邵东县八年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.【解答】解:∵在一个直角三角形中,有一个锐角等于65°,
∴另一个锐角的度数是90°﹣65°=25°.
故选:C.
2.【解答】解:A、42+32≠62,不是直角三角形,故此选项正确;
B、122+52=132,是直角三角形,故此选项错误;
C、62+82=102,是直角三角形,故此选项错误;
D、()2+()2=22,是直角三角形,故此选项错误;
故选:A.
3.【解答】解:作DE⊥AB于E,
∵∠C=90°,∠B=30°,
∴∠CAB=60°,又AD是∠BAC的平分线,
∴∠CAD=30°,
∴CD=AD,又AD=10,
∴CD=5,
∵AD是∠BAC的平分线,∠C=90°,DE⊥AB
∴DE=CD=5,
故选:B.
4.【解答】解:∵PD⊥AB,PE⊥AC,
∴∠ADP=∠AEP=90°,
在Rt△ADP和△AEP中,
∴Rt△ADP≌△AEP(HL),
故选:D.
5.【解答】解:A、正确,有三个角是直角的四边形是矩形是矩形的判定定理;
B、错误,对角线相等的四边形不一定是矩形,对角线相等的平行四边形才是矩形;
C、正确,对角线互相垂直的矩形是正方形;
D、正确,对角线互相垂直的平行四边形是菱形.
故选:B.
6.【解答】解:三条角平分线的交点到三角形三边的距离相等.
故选:A.
7.【解答】解:A、是轴对称图形,不是中心对称图形,故选项错误;
B、不是中心对称图形,故选项错误;
C、是中心对称图形,故选项正确;
D、是轴对称图形,不是中心对称图形,故选项错误.
故选:C.
8.【解答】解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD,
∵AC=8,BD=6,
∴AO=4,BO=3,
∴4﹣3<AB<4+3,
解得:1<AB<7,
故选:A.
9.【解答】解:设运动时间为t秒,则CP=12﹣3t,BQ=t,
根据题意得到12﹣3t=t,
解得:t=3,
故选:B.
10.【解答】解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=AC,OD=BD,AC=BD=6,
∴OC=OD=3,
∴四边形CODE是菱形,
∴DE=OC=OD=CE=3,
∴四边形CODE的周长=4×3=12.
11.【解答】解:∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,AC⊥BD,
又∵OE⊥OF,
∴∠EOB+∠BOF=90°=∠BOF+∠COF,
∴∠EOB=∠COF,
∴△BEO≌△CFO(ASA),
∴BE=CF=3,
又∵AB=BC,
∴AE=BF=4,
∴Rt△BEF中,EF===5.
故选:C.
12.【解答】解:由题意可得阴影部分面积等于正方形面积的,即是,
5个这样的正方形重叠部分(阴影部分)的面积和为×4,
n个这样的正方形重叠部分(阴影部分)的面积和为×(n﹣1)=cm2.
故选:C.
二.填空题(共6小题)
13.【解答】解:∵一个多边形的每个外角都等于36°,
∴多边形的边数为360°÷36°=10.
则这个多边形是十边形.
故答案为:十.
14.【解答】解:根据矩形的判定定理可知,已知了AD∥BC,∠D=90°,还缺的条件是∠A=90°或AB∥CD,或AD=BC.
15.【解答】解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
16.【解答】解:∵∠DBC=∠BAD+∠ADB,∠DBC=30°,∠BAD=15°,
∴∠BAD=∠ADB=15°,
∴BA=BD=260m,
在Rt△BDC中,∵∠DCB=90°,∠DBC=30°,
∴DC=BD=130m,
∵AF=BG=CE=1.6m,
∴DE=DC+CE=131.6m,
故答案为:131.6.
17.【解答】解:∵四边形ABCD是矩形,
∴BC=AD=10cm,∠B=∠C=∠D=90°,
由折叠的性质可得:AF=AD=10cm,∠AFE=∠D=90°,DE=EF,
∴BF===6(cm),
∴FC=BC﹣BF=10﹣6=4(cm),
∵EF2=CE2+CF2,
∴(8﹣CE)2=CE2+16,
∴EC=3cm
故答案为:3.
18.【解答】解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为:ab=×8=4,
∴4×ab+(a﹣b)2=25,
∴(a﹣b)2=25﹣16=9,
∴a﹣b=3,
故答案是:3.
三、解答题(本大题共2小题,每小题6分,满分12分)
19.【解答】解:设这个多边形的边数是,则
(n﹣2)×180=360×4,
n﹣2=8,
n=10.
答:这个多边形的边数是10.
20.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=10,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴BE=AB,
即△ABE是等腰三角形;
(2)解:由(1)可知BE=AB=6,AD=BC=10
∴CE=BC﹣BE=10﹣6=4.
四、解答题(本大题共2小题,每小题8分,满分16分)
21.【解答】证明:(1)在△ABC和△DCB中,∠A=∠D=90°,AC=BD,
根据勾股定理:AB2=BC2﹣AC2; DC2=BC2﹣BD2;
∴AB2=DC2=BC2﹣BD2,
∴AB=DC,
在Rt△ABC与Rt△DCB中
∴Rt△ABC≌Rt△DCB(HL)
(2)∵△ABC≌△DCB,则∠ACB=∠DBC,
在△OBC中,即∠OCB=∠OBC
∴△OBC是等腰三角形.
22.【解答】解:(1)∵四边形ABCD是菱形,对角线AC=8cm,BD=6cm,
∴=×8×6=24(cm2);
(2)∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
又∵AC=8cm,BD=6cm,
∴OA=OC=AC=4cm,OB=OD=BD=3cm,
在Rt△BOC中,由勾股定理得:BC===5(cm),
∵点E是AB的中点,
∴OE是△ABC的中位线,
∴OE=cm.
五、解答题(本大题共2小题,每小题9分,满分18分)
23.【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB中点,F是CD中点,
∴AE=CF,AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
同理:DE∥BF,
∴四边形GEHF是平行四边形.
24.【解答】证明:如图,
过D作DG⊥AB,交AB于点G,
∵∠C=∠DEC=∠DFC=90°,
∴四边形CEDF为矩形,
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG;
∵BD平分∠ABC,DG⊥AB,DE⊥BC,
∴DE=DG,
∴DE=DF,
∴四边形CEDF为正方形.
六、解答题(本大题共2小题,每小题10分,满分20分)
25.【解答】(1)证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO.
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由:
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4=×180°=90°.
即∠ECF=90°,
∴四边形AECF是矩形.
26.【解答】证明:(1)∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,,
∴△BAD≌△CAF(SAS),
∴BD=CF
∵BD+CD=BC,
∴CF+CD=BC;
(2)CF﹣CD=BC;
理由:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,,
∴△BAD≌△CAF(SAS)
∴BD=CF
∴BC+CD=CF,
∴CF﹣CD=BC;
(3)①∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴CD﹣BC=CF,
②∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,
∴∠BAD=∠CAF,
∵△BAD≌△CAF(SAS),
∴∠ACF=∠ABD,
∵∠ABC=45°,
∴∠ABD=135°,
∴∠ACF=∠ABD=135°,
∴∠FCD=90°,
∴△FCD是直角三角形.O为DF中点,
∴OC=DF.
∴DF=2OC=2,
∴正方形ADEF的边长为=2.
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.(3分)在一个直角三角形中,有一个锐角等于65°,则另一个锐角的度数是( )
A.115° B.125° C.25° D.35°
2.(3分)下列四组数据中,“不能”作为直角三角形的三边长的是( )
A.3,4,6 B.5,12,13 C.6,8,10 D.,,2
3.(3分)如图,Rt△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,AD=10,则点D到AB的距离是( )
A.8 B.5 C.6 D.4
4.(3分)如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PD=PE,则△APD与△APE全等的理由是( )
A.SAS B.AAA C.SSS D.HL
5.(3分)下列说法中,不正确的是( )
A.有三个角是直角的四边形是矩形
B.对角线相等的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.对角线互相垂直的平行四边形是菱形
6.(3分)下面哪个点到三角形三边的距离相等( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三角形内任意一点
7.(3分)下列图形属于中心对称图形的是( )
A. B.
C. D.
8.(3分)如图,平行四边形ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则AB长的取值范围是( )
A.1<AB<7 B.2<AB<4 C.6<AB<8 D.3<AB<4
9.(3分)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
10.(3分)如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10 B.12 C.18 D.24
11.(3分)如图所示,在正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的长为( )
A.3 B.4 C.5 D.6
12.(3分)如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
A.cm2 B.cm2 C.cm2 D.()ncm2
二.填空题(共6小题)
13.(3分)一个多边形的每一个外角都等于36°,它是 边形.
14.(3分)如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 (写出一种情况即可).
15.(3分)如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
16.(3分)如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测到到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,塔的高度DE= m.
17.(3分)如图,小红用一张长方形纸片ABCD进行折纸,使得顶点D落在边BC上的点F处(折痕为AE).已知该纸片AB为8cm,BC为10cm,则EC的长度为 cm.
18.(3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为 .
三、解答题(本大题共2小题,每小题6分,满分12分)
19.(6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
20.(6分)已知:如图,在?ABCD中,AE平分∠BAD,交BC于点E.
(1)求证:△ABE是等腰三角形;
(2)若AB=6,AD=10,求CE的长.
四、解答题(本大题共2小题,每小题8分,满分16分)
21.(8分)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)求证:△OBC是等腰三角形.
22.(8分)如图,菱形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,已知AC=8cm,BD=6cm,
(1)求菱形ABCD的面积.
(2)求OE的长度.
五、解答题(本大题共2小题,每小题9分,满分18分)
23.(9分)如图,在?ABCD中,若点E、F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
24.(9分)如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由(提示:可作DG⊥AB于点G)
六、解答题(本大题共2小题,每小题10分,满分20分)
25.(10分)如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
26.(10分)已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②正方形对角线AE,DF相交于点O,连接OC.若OC为,求正方形ADEF的边长.
2018-2019学年湖南省邵阳市邵东县八年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.【解答】解:∵在一个直角三角形中,有一个锐角等于65°,
∴另一个锐角的度数是90°﹣65°=25°.
故选:C.
2.【解答】解:A、42+32≠62,不是直角三角形,故此选项正确;
B、122+52=132,是直角三角形,故此选项错误;
C、62+82=102,是直角三角形,故此选项错误;
D、()2+()2=22,是直角三角形,故此选项错误;
故选:A.
3.【解答】解:作DE⊥AB于E,
∵∠C=90°,∠B=30°,
∴∠CAB=60°,又AD是∠BAC的平分线,
∴∠CAD=30°,
∴CD=AD,又AD=10,
∴CD=5,
∵AD是∠BAC的平分线,∠C=90°,DE⊥AB
∴DE=CD=5,
故选:B.
4.【解答】解:∵PD⊥AB,PE⊥AC,
∴∠ADP=∠AEP=90°,
在Rt△ADP和△AEP中,
∴Rt△ADP≌△AEP(HL),
故选:D.
5.【解答】解:A、正确,有三个角是直角的四边形是矩形是矩形的判定定理;
B、错误,对角线相等的四边形不一定是矩形,对角线相等的平行四边形才是矩形;
C、正确,对角线互相垂直的矩形是正方形;
D、正确,对角线互相垂直的平行四边形是菱形.
故选:B.
6.【解答】解:三条角平分线的交点到三角形三边的距离相等.
故选:A.
7.【解答】解:A、是轴对称图形,不是中心对称图形,故选项错误;
B、不是中心对称图形,故选项错误;
C、是中心对称图形,故选项正确;
D、是轴对称图形,不是中心对称图形,故选项错误.
故选:C.
8.【解答】解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD,
∵AC=8,BD=6,
∴AO=4,BO=3,
∴4﹣3<AB<4+3,
解得:1<AB<7,
故选:A.
9.【解答】解:设运动时间为t秒,则CP=12﹣3t,BQ=t,
根据题意得到12﹣3t=t,
解得:t=3,
故选:B.
10.【解答】解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=AC,OD=BD,AC=BD=6,
∴OC=OD=3,
∴四边形CODE是菱形,
∴DE=OC=OD=CE=3,
∴四边形CODE的周长=4×3=12.
11.【解答】解:∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,AC⊥BD,
又∵OE⊥OF,
∴∠EOB+∠BOF=90°=∠BOF+∠COF,
∴∠EOB=∠COF,
∴△BEO≌△CFO(ASA),
∴BE=CF=3,
又∵AB=BC,
∴AE=BF=4,
∴Rt△BEF中,EF===5.
故选:C.
12.【解答】解:由题意可得阴影部分面积等于正方形面积的,即是,
5个这样的正方形重叠部分(阴影部分)的面积和为×4,
n个这样的正方形重叠部分(阴影部分)的面积和为×(n﹣1)=cm2.
故选:C.
二.填空题(共6小题)
13.【解答】解:∵一个多边形的每个外角都等于36°,
∴多边形的边数为360°÷36°=10.
则这个多边形是十边形.
故答案为:十.
14.【解答】解:根据矩形的判定定理可知,已知了AD∥BC,∠D=90°,还缺的条件是∠A=90°或AB∥CD,或AD=BC.
15.【解答】解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
16.【解答】解:∵∠DBC=∠BAD+∠ADB,∠DBC=30°,∠BAD=15°,
∴∠BAD=∠ADB=15°,
∴BA=BD=260m,
在Rt△BDC中,∵∠DCB=90°,∠DBC=30°,
∴DC=BD=130m,
∵AF=BG=CE=1.6m,
∴DE=DC+CE=131.6m,
故答案为:131.6.
17.【解答】解:∵四边形ABCD是矩形,
∴BC=AD=10cm,∠B=∠C=∠D=90°,
由折叠的性质可得:AF=AD=10cm,∠AFE=∠D=90°,DE=EF,
∴BF===6(cm),
∴FC=BC﹣BF=10﹣6=4(cm),
∵EF2=CE2+CF2,
∴(8﹣CE)2=CE2+16,
∴EC=3cm
故答案为:3.
18.【解答】解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为:ab=×8=4,
∴4×ab+(a﹣b)2=25,
∴(a﹣b)2=25﹣16=9,
∴a﹣b=3,
故答案是:3.
三、解答题(本大题共2小题,每小题6分,满分12分)
19.【解答】解:设这个多边形的边数是,则
(n﹣2)×180=360×4,
n﹣2=8,
n=10.
答:这个多边形的边数是10.
20.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=10,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴BE=AB,
即△ABE是等腰三角形;
(2)解:由(1)可知BE=AB=6,AD=BC=10
∴CE=BC﹣BE=10﹣6=4.
四、解答题(本大题共2小题,每小题8分,满分16分)
21.【解答】证明:(1)在△ABC和△DCB中,∠A=∠D=90°,AC=BD,
根据勾股定理:AB2=BC2﹣AC2; DC2=BC2﹣BD2;
∴AB2=DC2=BC2﹣BD2,
∴AB=DC,
在Rt△ABC与Rt△DCB中
∴Rt△ABC≌Rt△DCB(HL)
(2)∵△ABC≌△DCB,则∠ACB=∠DBC,
在△OBC中,即∠OCB=∠OBC
∴△OBC是等腰三角形.
22.【解答】解:(1)∵四边形ABCD是菱形,对角线AC=8cm,BD=6cm,
∴=×8×6=24(cm2);
(2)∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
又∵AC=8cm,BD=6cm,
∴OA=OC=AC=4cm,OB=OD=BD=3cm,
在Rt△BOC中,由勾股定理得:BC===5(cm),
∵点E是AB的中点,
∴OE是△ABC的中位线,
∴OE=cm.
五、解答题(本大题共2小题,每小题9分,满分18分)
23.【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB中点,F是CD中点,
∴AE=CF,AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
同理:DE∥BF,
∴四边形GEHF是平行四边形.
24.【解答】证明:如图,
过D作DG⊥AB,交AB于点G,
∵∠C=∠DEC=∠DFC=90°,
∴四边形CEDF为矩形,
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG;
∵BD平分∠ABC,DG⊥AB,DE⊥BC,
∴DE=DG,
∴DE=DF,
∴四边形CEDF为正方形.
六、解答题(本大题共2小题,每小题10分,满分20分)
25.【解答】(1)证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO.
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由:
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4=×180°=90°.
即∠ECF=90°,
∴四边形AECF是矩形.
26.【解答】证明:(1)∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,,
∴△BAD≌△CAF(SAS),
∴BD=CF
∵BD+CD=BC,
∴CF+CD=BC;
(2)CF﹣CD=BC;
理由:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,,
∴△BAD≌△CAF(SAS)
∴BD=CF
∴BC+CD=CF,
∴CF﹣CD=BC;
(3)①∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴CD﹣BC=CF,
②∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,
∴∠BAD=∠CAF,
∵△BAD≌△CAF(SAS),
∴∠ACF=∠ABD,
∵∠ABC=45°,
∴∠ABD=135°,
∴∠ACF=∠ABD=135°,
∴∠FCD=90°,
∴△FCD是直角三角形.O为DF中点,
∴OC=DF.
∴DF=2OC=2,
∴正方形ADEF的边长为=2.
同课章节目录
