六年级下册数学课件-圆柱的表面积和体积习题课 冀教版(17张ppt)
文档属性
| 名称 | 六年级下册数学课件-圆柱的表面积和体积习题课 冀教版(17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 853.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 11:16:54 | ||
图片预览





文档简介
(共17张PPT)
圆柱的表面积和体积习题课
底面
底面
圆柱的两个圆面叫作底面,
圆柱的上、下两个面都是圆,并且大小一样。
圆柱有一个曲面。
曲面叫作侧面。
两底面之间的距离叫作高,圆柱有无数条高。
圆柱有哪些特征呢?
侧面
1.圆柱的特征
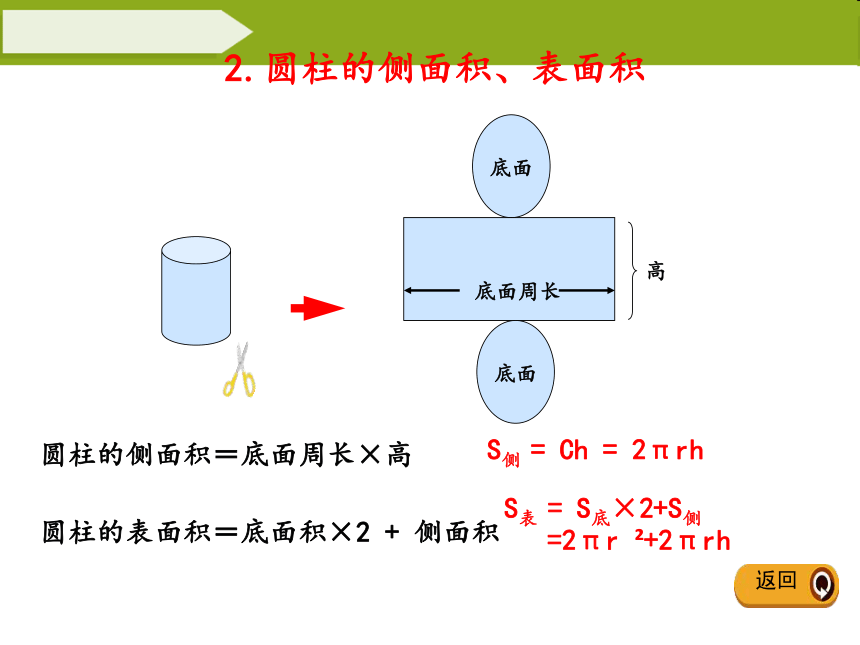
2.圆柱的侧面积、表面积
圆柱的侧面积=底面周长×高
高
底面周长
圆柱的表面积=底面积×2 + 侧面积
S侧 = Ch = 2πrh
S表 = S底×2+S侧
=2πr ?+2πrh
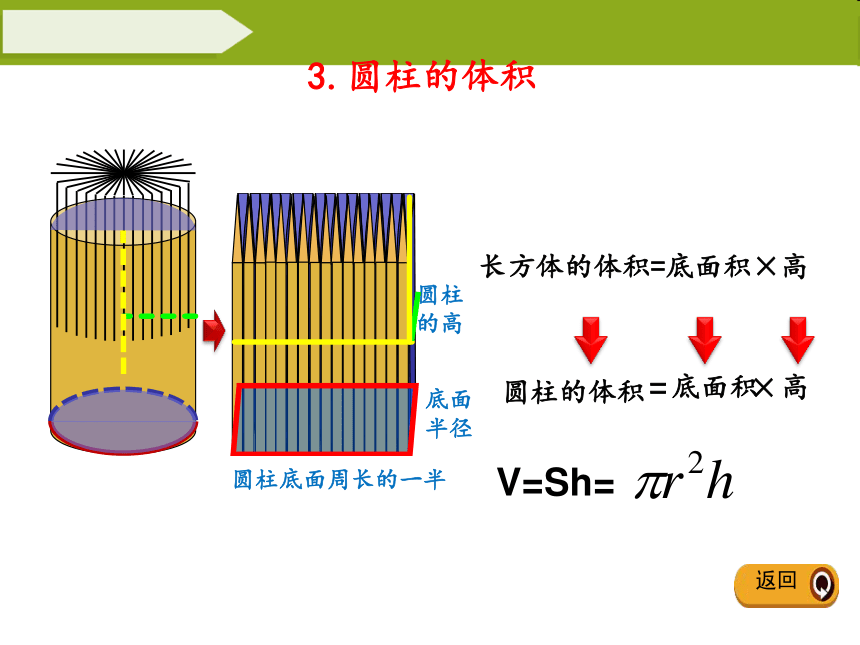
3.圆柱的体积
圆柱底面周长的一半
圆柱的高
底面
半径
底面积
高
圆柱的体积
长方体的体积=底面积×高
基本题型:
1.已知半径和高求表面积
一个圆柱的底面半径是5厘米,高是14厘米。它的表面积是多少?
2.已知直径和高求表面积
一个圆柱的底面直径是20厘米,高是15厘米。它的表面积是多少?
侧面积:20×3.14×15
=62.8×15
=942(平方厘米)
表面积:942+628=1570(平方厘米)
3.已知底面周长和高求表面积
一个圆柱的底面周长是6.28分米,高是6分米,它的表面积是多少?
侧面积:6.28×6=37.68(平方分米)
表面积:37.68+6.28=43.96(平方分米)
4.一个圆柱的底面直径是4分米,它的侧面展开图正好是一个正方形,这个圆柱的高是多少分米?
底面周长=高
高:4×3.14=12.56(分米)
5.一节铁皮烟囱长1.5米,直径0.2米,做这样一节烟囱,至少要用多少铁皮多少平方米?(接缝处忽略不计)
一节烟囱用的铁皮是圆柱的侧面积
0.2×3.14×1.5=0.942(平方米)
6.一个圆柱的底面半径扩大3倍,高不变,它的侧面积扩大( )倍。
3
7.有一个长方形长10厘米,宽5厘米,如果以长为轴旋转一周,可以得到一个( )。这个图形的高是( ),底面半径是( ):如果以宽为轴旋转一周,可以得到一个( ),这个图形的高是( ),底面半径是( ).
圆柱
10厘米
5厘米
圆柱
5厘米
10厘米
结论1:一个长方形,不管以长为轴,还是以宽为轴,得到的都是圆柱形状,以谁为轴谁就是高,另一边就是底面半径。两种情况体积,表面积都不同。
结论2:一张长方形纸,围成一个圆柱形状。有两种围法。但是侧面积都是这个长方形的面积。所以侧面积不变。
8. 一个圆柱的底面半径扩大3倍,高不变,它的体积扩大( )倍。
9.圆柱的底面等分16份,把圆柱切开,能拼成一个近似(长方体),长方体的底面积就是圆柱的( ),长方体的高就是圆柱的( )。长方体体积=( ),所以圆柱体积=( )
9
底面积
高
圆柱的体积
底面积×高
三、一个圆柱的底面积是20平方厘米,从中间将它切成两个小圆柱,这时表面积增加了( )
40平方厘米
E
B
AD
C
求体积的题有五种类型
第一种: 已知底面积和高。
例题:S=28.26平方分米 h=8分米
28.26×8=226.08(立方分米)
第二种:已知底面半径和高。
r=10cm h=5cm
第四种:已知底面周长和高
C=94.2m h=4m
第三种:已知底面直径和高
d=10cm h=5cm
第五种:已知一种立体图形的体积,锻造成圆柱。 关键点:立体图形和圆柱的体积相同
例题:一根方钢长50厘米,底面是边长15厘米的正方形。如果把它锻造成底面积是90平方厘米的圆柱形钢材。这根钢材长多少厘米?
方钢体积:15×15×50
=225×50
=11250(立方厘米)
钢材的长:11250÷90=125(厘米)
长方体的体积就是圆柱的体积
长方体的体积=圆柱的体积
2
3.把一段长8分米的圆柱形钢铁截成两段后,表面积的总和比原来增加了6平方分米,这段钢铁原来的体积是多少立方分米?
底面积:6÷2=3(平方分米)
体积:3×8=24 (立方分米)
4.一个量杯的底面积是113.04平方厘米,把一个土豆浸没在水中后,水面升高了4厘米。求这个土豆的体积。
113.04×4=452.16 (立方厘米)
圆柱的表面积和体积习题课
底面
底面
圆柱的两个圆面叫作底面,
圆柱的上、下两个面都是圆,并且大小一样。
圆柱有一个曲面。
曲面叫作侧面。
两底面之间的距离叫作高,圆柱有无数条高。
圆柱有哪些特征呢?
侧面
1.圆柱的特征
2.圆柱的侧面积、表面积
圆柱的侧面积=底面周长×高
高
底面周长
圆柱的表面积=底面积×2 + 侧面积
S侧 = Ch = 2πrh
S表 = S底×2+S侧
=2πr ?+2πrh
3.圆柱的体积
圆柱底面周长的一半
圆柱的高
底面
半径
底面积
高
圆柱的体积
长方体的体积=底面积×高
基本题型:
1.已知半径和高求表面积
一个圆柱的底面半径是5厘米,高是14厘米。它的表面积是多少?
2.已知直径和高求表面积
一个圆柱的底面直径是20厘米,高是15厘米。它的表面积是多少?
侧面积:20×3.14×15
=62.8×15
=942(平方厘米)
表面积:942+628=1570(平方厘米)
3.已知底面周长和高求表面积
一个圆柱的底面周长是6.28分米,高是6分米,它的表面积是多少?
侧面积:6.28×6=37.68(平方分米)
表面积:37.68+6.28=43.96(平方分米)
4.一个圆柱的底面直径是4分米,它的侧面展开图正好是一个正方形,这个圆柱的高是多少分米?
底面周长=高
高:4×3.14=12.56(分米)
5.一节铁皮烟囱长1.5米,直径0.2米,做这样一节烟囱,至少要用多少铁皮多少平方米?(接缝处忽略不计)
一节烟囱用的铁皮是圆柱的侧面积
0.2×3.14×1.5=0.942(平方米)
6.一个圆柱的底面半径扩大3倍,高不变,它的侧面积扩大( )倍。
3
7.有一个长方形长10厘米,宽5厘米,如果以长为轴旋转一周,可以得到一个( )。这个图形的高是( ),底面半径是( ):如果以宽为轴旋转一周,可以得到一个( ),这个图形的高是( ),底面半径是( ).
圆柱
10厘米
5厘米
圆柱
5厘米
10厘米
结论1:一个长方形,不管以长为轴,还是以宽为轴,得到的都是圆柱形状,以谁为轴谁就是高,另一边就是底面半径。两种情况体积,表面积都不同。
结论2:一张长方形纸,围成一个圆柱形状。有两种围法。但是侧面积都是这个长方形的面积。所以侧面积不变。
8. 一个圆柱的底面半径扩大3倍,高不变,它的体积扩大( )倍。
9.圆柱的底面等分16份,把圆柱切开,能拼成一个近似(长方体),长方体的底面积就是圆柱的( ),长方体的高就是圆柱的( )。长方体体积=( ),所以圆柱体积=( )
9
底面积
高
圆柱的体积
底面积×高
三、一个圆柱的底面积是20平方厘米,从中间将它切成两个小圆柱,这时表面积增加了( )
40平方厘米
E
B
AD
C
求体积的题有五种类型
第一种: 已知底面积和高。
例题:S=28.26平方分米 h=8分米
28.26×8=226.08(立方分米)
第二种:已知底面半径和高。
r=10cm h=5cm
第四种:已知底面周长和高
C=94.2m h=4m
第三种:已知底面直径和高
d=10cm h=5cm
第五种:已知一种立体图形的体积,锻造成圆柱。 关键点:立体图形和圆柱的体积相同
例题:一根方钢长50厘米,底面是边长15厘米的正方形。如果把它锻造成底面积是90平方厘米的圆柱形钢材。这根钢材长多少厘米?
方钢体积:15×15×50
=225×50
=11250(立方厘米)
钢材的长:11250÷90=125(厘米)
长方体的体积就是圆柱的体积
长方体的体积=圆柱的体积
2
3.把一段长8分米的圆柱形钢铁截成两段后,表面积的总和比原来增加了6平方分米,这段钢铁原来的体积是多少立方分米?
底面积:6÷2=3(平方分米)
体积:3×8=24 (立方分米)
4.一个量杯的底面积是113.04平方厘米,把一个土豆浸没在水中后,水面升高了4厘米。求这个土豆的体积。
113.04×4=452.16 (立方厘米)
