人教版八年级数学下册18章平行四边形全章导学案(11学时 无答案)
文档属性
| 名称 | 人教版八年级数学下册18章平行四边形全章导学案(11学时 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 00:00:00 | ||
图片预览




文档简介
第18章 平行四边形
18.1.1平行四边形及性质(1)(第1课时)
学生信息班级 姓名
学习目标:1、掌握平行四边形的概念和对边相等对角相等的性质,根据概念和性质进行有关的计算和证明.
2、让学生学会用分析法和综合法解决问题
学习重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
学习难点:运用平行四边形的性质进行有关的论证和计算.
一、学前准备
1、定义:两组对边分别 的四边形叫平行四边形。
2、表示:平行四边形ABCD记作
二、合作探究
1.平行四边形的性质1:
边的性质:AB∥ ; BC∥
AB= ; BC=
即:平行四边形对边平行且 。
2.平行四边形的性质2: 角的性质:∠A= ,∠B=
即:平行四边形对角 。
3.平行四边形的性质:几何语言描述平行四边形的性质,
①∵四边形ABCD是平行四边形
∴ AB∥ ,AD∥
∴ AB = , AD =
②∵四边形ABCD是平行四边形
∴ ∠A=∠ , ∠B=∠
③∵四边形ABCD是平行四边形
∴AB∥CD,∴∠A与∠D互为邻补角,
∠A+∠D= , ∠B+∠C=
三、随堂练习
1、在 ABCD中,AB=3㎝,AD=5㎝,∠A=43°,∠B=137°,则DC= ,AD=
∠C= ,∠D= .其周长为 。
2、在?ABCD中∠A:∠B=4:5 ,那么∠C= ,∠D=_______.
3.已知?ABCD中,∠A比∠B小20°,则∠D的度数是( )
A.60° B.80° C.100° D.120°
4.在ABCD中,已知∠B=40,求其他各个内角的度数。
四、学习体会
五、课后学效检测与拓展
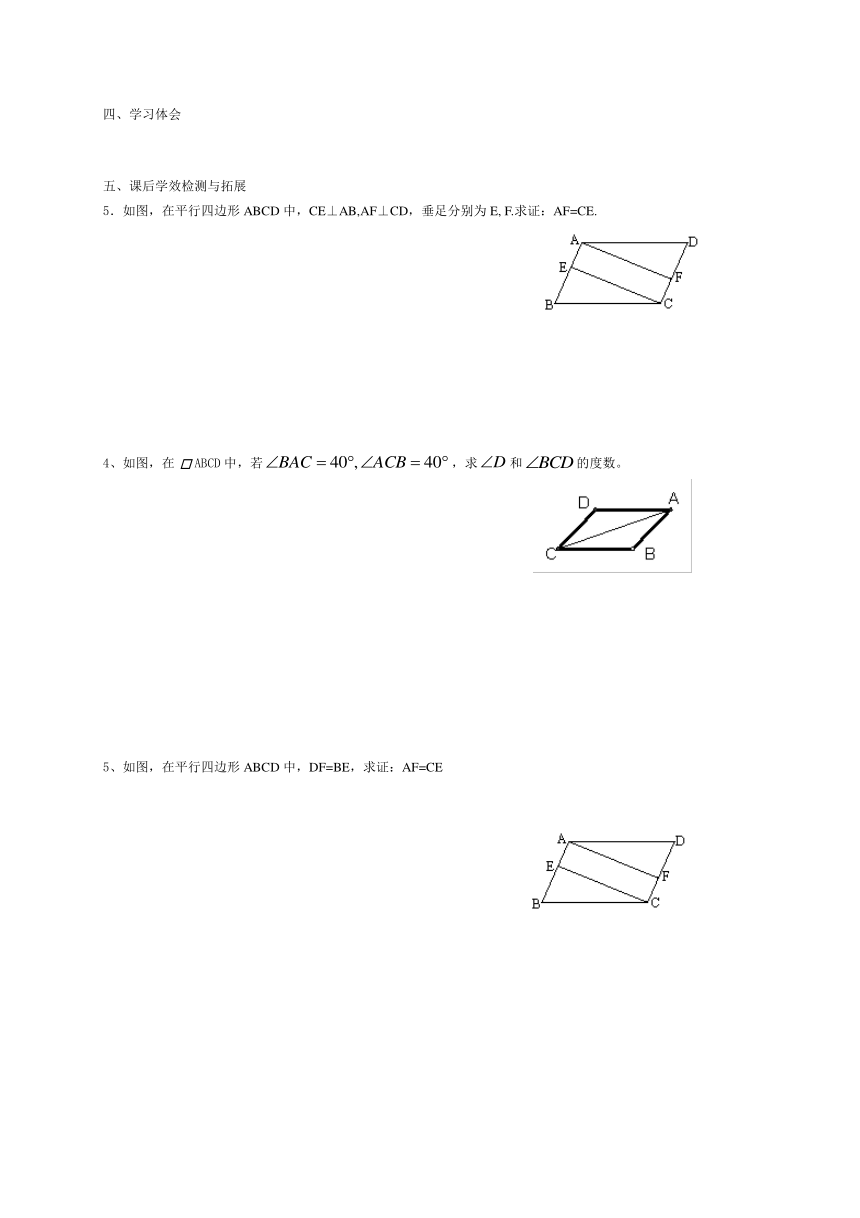
5.如图,在平行四边形ABCD中,CE⊥AB,AF⊥CD,垂足分别为E, F.求证:AF=CE.
4、如图,在 ABCD中,若,求和的度数。
5、如图,在平行四边形ABCD中,DF=BE,求证:AF=CE
18.1.1.2 平行四边形的性质(2)(第2课时)
学生信息班级 姓名
学习目标:1、掌握平行四边形的性质:平行四边形的对角线互相平分。
2、会运用平行四边形的性质进行推理和计算。
学习重点:平行四边形对角线互相平分的性质,以及性质的应用.
学习难点:综合运用平行四边形的性质进行有关的论证和计算.
一、学前准备
① 的四边形叫做平行四边形。
②平行四边形对边平行且 ;平行四边形对角 。
③两条平行线之间的任何两条平行线段都 。
二、合作探究
1.平行四边形的性质3:对角线的性质
已知:如图,?ABCD中,对角线AC和BD相交于点O,求证:OA=OC,OB=OD。
证明: ∵?ABCD是平行四边形
∴ ∥ ; = ;
∴∠ =∠ ,
在△ 和△ 中,
∴△ ≌△
∴
即平行四边形的对角线互相平分。
用几何语言
∵四边形ABCD是平行四边形
∴AO= = , BO= = ,
三、随堂练习
1、判断对错
(1)在ABCD中,AC交BD于O,则AO=OB=OC=OD. ( )
(2)平行四边形两条对角线的交点到一组对边的距离相等.( )
(3)平行四边形的两组对边分别平行且相等. ( )
(4)平行四边形是轴对称图形. ( )
2、如图,已知AB=5㎝,AD=8㎝,AC=6㎝, BD=12㎝,则AO= = ㎝,BO= = ㎝,△AOB的周长是 ㎝
3、平行四边形的对角线把平行四边形分成了 对全等的三角形。
4、在 ABCD中,两条对角线AC、BD相交于点O,指出图形中所有相等的线段。
5.如图,在ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为20,AB=8,那么对角线AC与BD的和是多少?
解:∵△AOB的周长为20(已知)
∴ + +AB=20,
∵AB=8
∴AO+BO=
∵在ABCD中,
∴AO = = ,,BO= = ,(平行四边形对角线 )
∴AC+BD = 2 +2 =2( )=
答:对角线AC和BD的和是 。
四、学习体会
五、课后学效检测与拓展
1、已知四边形ABCD是平行四边形,AB=5cm,BC=4cm,AC⊥BC,求BC、CD、AC、OA的长以及ABCD的面积.
2、如图,在ABCD中,BC=10,AC=8,BD=14.△AOD的周长为多少?△ABC与△DBC的周长哪个长?长多少?
18.1.2.1平行四边形的判定(1)(第3课时)
学生信息班级 姓名
学习目标:1、明确平行四边形的判定方法。
2、能运用平行四边形的判定,解决简单的实际问题。
学习重点:平行四边形的判定方法及应用.
学习难点:平行四边形的判定定理与性质定理的灵活应用.
一、学前准备
1、平行四边形的定义:
两组对边分别 的四边形叫做平行四边形。
-------定义就是平行四边形的一种判定方法
用几何语言表示:∵_________//___________
_________//____________
∴四边形ABCD是____________
2、平行四边形的性质:
(1)边的性质:平行四边形的对边 ;
几何语言:在 ABCD中,AD BC,AB DC;
(2)角的性质:平行四边形的对角 ;
几何语言:在ABCD中,∠A= ,∠B= ;
(3)对角线的性质:平行四边形的对角线 ;
几何语言:在ABCD中,OA= = ;OB= = ;
二、合作探究
已知:四边形ABCD, AB=CD,AD=BC求证:四边形ABCD是平行四边形
证明:连结AC,
在△ABC和△CDA中
归纳:判定定理一:两组对边分别相等的四边形是平行四边形
用几何语言表示:∵_________=___________
_________=____________
∴四边形ABCD是____________
2、类似地,我们还可以得出几个平行四边形的判定定理:
判定定理二:两组对角分别相等的四边形是平行四边形
用几何语言表示:∵∠_________=∠___________
∠_________=∠____________
∴四边形ABCD是____________
判定定理三:对角线互相平分的四边形是平行四边形
用几何语言表示:∵_________=___________
_________=____________
∴四边形ABCD是____________
三、随堂练习
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等 (B)两条对角线互相平分
(C)两条对角线相等 (D)两组对边分别平行
2、四边形ABCD中,AB∥CD,当满足下列哪个条件时,四边形ABCD是平行四边形( )
(A)∠B+∠C=180° (B) ∠A+∠B=180° (C) ∠A+∠D=180° (D) ∠A+∠C=180°
3、在四边形ABCD中,若∠B=∠D,那么再添加一个条件:____________,就可以判定ABCD是平行四边形。
4、如右图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=___ _cm,
CD=___ _cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=__ _cm,
DO=__ _cm时,四边形ABCD为平行四边形.
四、学习体会
五、课后学效检测与拓展
1、如图,在平行四边形ABCD中,E、F、G、H分别是各边中点。
求证:四边形EFGH是平行四边形。
2、如图,平行四边形ABCD的对角线AC,BD相交于点O,点 E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形
18.1.2.2平行四边形的判定(2)(第4课时)
学生信息班级 姓名
学习目标:1、掌握用一组对边平行且相等来判定平行四边形的方法
2、理解和领会三角形三角形中位线定理及其应用
3、会综合应用平行四边形的四种判定方法和性质来证明问题
学习重点:平行四边形各种判定方法及其应用,尤其是根据不同条件能正确地选择判定方法.
学习难点:平行四边形的判定定理与性质定理的综合应用.
一、自主学习
1、判定平行四边形的方法有哪几个:①
② ③ 。
2、预习课本第46—49页
3、如右图所示,△ABC各边的中点分别是D、E、F,则在△ABC中,中位线有那几条:
二、合作探究
1、已知:四边形ABCD, AB∥CD,AB=CD,求证:四边形ABCD是平行四边形
证明:连结AC,
总结:平行四边形的判定定理:
2、点D、E分别是△ABC的边AB、AC的中点,求证:DE∥BC、DE=.
总结:三角形的中位线定理:
三、随堂练习
1、判断题:
(1)一组对边平行,另一组对边相等的四边形是平行四边形; ( )
(2)对角线互相平分的四边形是平行四边形. ( )
(3)两组对角分别相等的四边形是平行四边形; ( )
2、已知一个三角形的三边长分别为5㎝,7cm,8㎝,则连接各边中点所形成的三角形的周长为 cm。
3、三角形的一条中位线分三角形所形成的新三角形与原三角形的周长之和为60㎝,则原三角形的周长为 cm。
4、如图,△ABC中,DE是△ABC的中位线、F是BC的中点,
(1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm;
(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.
5、已知:如图,ABCD中,E、F分别是AC上两点,BE∥DF,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
四、学习体会
五、课后学效检测与拓展
已知:如图2、已知:如图(1),在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
18.2.1矩形的性质(第5课时)
学生信息班级 姓名
学习目标:1、了解矩形与平行四边形的关系;
2、初步认识矩形性质。
3.直角三角形斜边上的中线的性质,并能运用相关性质求解。
学习重点:矩形的性质.
学习难点:矩形的性质的灵活应用.
一、学前准备
1、①四边形ABCD是平行四边形 的三个性质:
②四边形ABCD的判定定理
③ 连接三角形两边中点的线段叫做 ,三角形的中位线平行于 ,并且等于第三边的 。
2、预习课本第52—53页
二、合作探究
1、矩形的定义:
2.矩形的性质:(在旁边的空白处画一个矩形并通过观察或度量进行归纳)
(1)边: ;
(2)角: ;
(3)对角线: 。
归纳:(几何语言)
平行四边形 矩形
图形
边 AB∥DC,AD∥ ,AB=DC,AD BC AB∥ ,AD∥ ,AB=DC,AD BC
角
对角线
小结1.:矩形是 的平行四边形
小结2.:矩形的两条对角线 。
3、观察下面三个图形,你能从中看到什么?
AO=BO= = = =
BO是斜边 上的 线。BO= = =
结论:直角三角形斜边上的中线等于 的一半。
三、随堂练习
1.矩形ABCD的对角线,则另一条对角线。
2.矩形的定义中有两个条件:一是 ,二是 .
3.直角三角形斜边上的中线长时8㎝,则斜边是 ㎝ 。
4.已知矩形ABCD,AC=8,则BD= ,OD= 。
5.已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
6.矩形不一定具有的性质是( )
A、对角线相等 B、四个角相等 C、是轴对称图形 D、对角线互相垂直
7.已知矩形的周长是24cm,相邻两边之比是,那么这个矩形的边长分别是 。
8.如图,已知矩形ABCD,AC=4,则BD= ,∠ABC= ;若∠ADB=40°,则∠ACB= °,
∠BDC= °,∠COD= °。
四、学习体会
五、课后学效检测与拓展
如图,在矩形ABCD中,E是CD上的一点,,且,
求的度数。
18.2.1矩形的判定(第6课时)
学生信息班级 姓名
学习目标:1、掌握矩形的判定方法。
2、能运用矩形的判定方法解决有关问题。
学习重点:矩形的判定.
学习难点:矩形的判定及性质的综合应用.
一、学前准备
1.矩形的性质:(1)对边 且 。(2)四个角都是 。(3)对角线 且 。
2.已知一个矩形的长时2cm,宽是1cm,它的对角线长是 。
3.在矩形ABCD中,AB=3,AC=5,则BC= ,这个矩形的面积是 。
二、合作探究(教材p54页)
1、定义:有一个角是 的平行四边形是矩形。
几何语言,如图∵ ABCD中,∠A= °,
∴ ABCD是
2、对角线相等的平行四边形是矩形。
几何语言:如图∵ ABCD中,______=_______
∴ ABCD是 。
3、有三个角是直角的四边形是矩形。
几何语言:如图 在四边形ABCD中
∵∠ =∠ =∠ = °
∴四边形ABCD是 。
如图,在ABCD中,对角线AC,BD相较于点OB=OC,∠OBA=60°.求∠OBC的度数。
三、随堂练习
1、如右图,已知四边形ABCD中,OA=OB=OC=OD=5cm,
则四边形ABCD是 。理由: 。
2.ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,且AB=4,则ABCD是 形,则它的面积是 。
3.下列说法中,不能判定四边形是矩形的是( )
A 对角线相等的平行四边形 B 对角线互相平分的四边形
C 四个角都相等的四边形 D 有一个角等于90°的平行四边形
4、如图,中,AB=6,BC=8,AC=10,求证:四边形ABCD是矩形
四、学习体会
五、课后学效检测与拓展
1、如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2,它是一个矩形吗?为什么?
2.已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形。
18.2.2菱形的性质(第7课时)
学生信息班级 姓名
学习目标:1、了解菱形与平行四边形的关系; 2、初步认识菱形的特征。
学习重点::菱形的性质.
学习难点:菱形的性质及菱形知识的综合应用.
一、学前准备
如图,在中,
①∵四边形ABCD是平行四边形
∴ AB∥ ,AD∥
AB = , AD =
②∵四边形ABCD是平行四边形
∴ ∠A=∠ , ∠B=∠
③∵四边形ABCD是平行四边形
∴AO= = , BO= = ,
二、合作探究
1、菱形的定义:
2.菱形的特征:(在旁边的空白处画一个菱形并通过观察或度量进行归纳)
(1)边: ;
(2)角: ;
(3)对角线: 。
平行四边形 菱形
图形
边 AB∥DC,AD∥ AB=DC,AD BC AB∥ ,AD∥
角
对角线
已知菱形ABCD的边长为40cm,,对角线AC、BD相交于点O,求这个菱形的两条对角线AC与BD的长。以及菱形ABCD的面积。(参考教材56页例3)
三、随堂练习
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4,则AC= .BD=
2.已知菱形ABCD的对角线AC与BD相交于点O,请说明菱形ABCD的面积等于。
解:菱形ABCD
,
= =
小结:菱形的面积等于两条对角线
3、在菱形ABCD中,∠BAD=60°,则∠ADC= °,∠DCA= °,
∠BAC= °,∠ADB= ,∠CBD= °
4、如图,在菱形ABCD中,,两条对角线相交于点O,若,,AB= 对角线,则菱形的周长是 ,面积是 。
四、学习体会
五、课后学效检测与拓展
1、已知菱形ABCD的边长为5cm,对角线AC长6cm,则另一条对角线BD长为 cm,菱形的面积为:
2、如图,在菱形ABCD中,∠BAD=2∠B,试说明△ABC是等边三角形。
18.2.2菱形的判定(第8课时)
学生信息班级 姓名
学习目标:1、掌握菱形的判定方法;2、能运用菱形的判定方法解决有关问题。
学习重点:菱形的两个判定方法.
学习难点:判定方法的证明方法及运用.
一、复习回顾:
(1)菱形的定义: ;
(2)菱形的性质1 : ;
性质2 : ;
(3)菱形的特征
A:对边 ________,四条边都 。
B:对角 。
C:两条对角线互相 ,并且每一条对角线平分 。
(4)菱形的面积等于两条对角线 。
二、自主学习(预习p57-58页)
1、菱形的识别:
方法一:有一组邻边 的平行四边形是菱形。(定义)
几何语言:∵ ABCD中,AB=
∴ ABCD是 。
方法二:对角线互相垂直的平行四边形是菱形
(即:平行四边形+对角线 菱形
几何语言:如图∵ ABCD中,______⊥_______
∴ ABCD是 。
方法三: 四条边都 的四边形是菱形。
几何语言:∵四边形ABCD中,AB BC CD DA
∴四边形ABCD是菱形。
三、合作探究
例题1:如图 ABCD的对角线AC,BD相交于点O,且AB=10,AO=8,BO=6.求证, ABCD是菱形。
例题2:在中,对角线AC平分∠DAB,这个四边形是菱形吗?简述理由
四、随堂练习
1.在中,若一条对角线平分一个内角,这个平行四边形是 形。
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和6,是一个特殊的平行四边形吗?为什么?求出它的面积。
3.如图,AE//BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,
求证:四边形ABCD是菱形。
五、学习体会
六、课后学效检测与拓展
1、已知四边形ABCD是平行四边形,请补充一个条件 ,使四边形ABCD成为菱形
2、如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证四边形AFCE是菱形.
证明:
18.2.3正方形的性质(第9课时)
学生信息班级 姓名
学习目标:1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别。
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
一、学前准备
(预习教材p58-59页)
二、合作探究
1、有一组_______相等并且有一个角是________的平行四边形叫做正方形。有一个角是________的菱形叫做正方形;一组________相等的矩形叫做正方形。
2、正方形既是_____,又是_____,所以它具有_____ 和 _____ 的性质:
(1)正方形的四个角都是_____ ,四条边都 _____ ;
(2)正方形的对角线_____且 ________,每条对角线平分__________;
(3)正方形是_______图形,____________的交点是它的对称中心;
(4)正方形是_______图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴。
3、见教材P59图18.2-12,正方形ABCD的对角线把它分成了____个三角形,它们是_____三角形,它们全等吗?请简单说明
理由____________________________________________________。
三、随堂练习
1、下列正方形具有而一般菱形不具有的性质是 ( )
A. 四条边都相等 B. 对角线互相垂直平分 C. 对角线相等 D. 每一条对角线平分一组对角
2、正方形具有而一般矩形不一定具有的性质是 ( )
A. 四个角相等 B. 四条边相等 C. 对角线互相平分 D. 对角线相等
3、已知一个正方形的边长为2cm,则对角线长为______。
4、已知一正方形的对角线长为2cm,则它的边长为_______。
5、若正方形的一条对角线长为4cm,则正方形的周长为______,面积为________;
对角线的交点到边的距离为_______。
6、顺次连接正方形各边中点,得4个等腰直角三角形,则每个小三角形的面积为原正方形面积的 ______ 。
7、如图,四边形ABCD是正方形,∠CAB是多少度?为什么?至少用两种方法说明理由。
四、学习体会
五、课后学效检测与拓展
1、正方形是轴对称图形,它的对称轴有____条,正方形也中心对称图形,它的对称中心是________。
2如图,在正方形ABCD中,∠DAE=25°,AE交对角线BD于E点,
那么∠BEC等于( )
A、45° B、60° C、70° D、75°
3、如图,E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD与∠ECD的度数.
4、如图,点E是正方形ABCD边CD上的一点,点F是CB和延长线上的点,且EAAF。
求证:DE=BF。
18.2.3正方形的性质(2)(第10课时)
学生信息班级 姓名
学习目标:1、了解正方形与平行四边形的关系;2、认识正方形的特征。
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
一、自主学习
1、正方形的定义:
矩形是 的平行四边形,菱形是 平行四边形
而:有一个角是直角,且有一组邻边相等的 是正方形。
2、正方形的性质:(在旁边空白处画一个正方形,并能过观察或度量归纳正方形的特征)
(1)边:
(2)角:
(3)对角线:
二、合作探究(小组交流合作并展示归纳)
平行四边形 矩形 菱形 正方形
图形
边 AB∥DC,AD∥ AB=DC,AD BC AB∥ ,AD∥ AB=DC,AD BC AB∥ ,AD∥ AB∥ ,AD∥
角
对角线 (1) (1) (2) (3)一条对角线平分一组对角 (1)(3)(同菱形)
注:矩形,菱形,正方形都是 的平行四边形。
三、随堂练习
1、正方形具有而菱形不一定具有的性质是( )
A 对角线互相平分 C 对角线相等
B 内角和为360? D 对角线平分内角
2、正方形具备而矩形不一定具备的性质是( )
A 四个角都是直角 C 四条边相等
B 对角线相等 D 对角线互相平分
3、下列说法错误的是( )
A 正方形的四条边相等 B 正方形的四个角相等
C 平行四边形对角线互相垂直 D 正方形的对角线相等
4、在正方形ABCD中,AO=5,则BO= ,BD= ;∠ABC= °
5、如图,在正方形ABCD中,对角线AC与BD相交于点O,则
,,。
6、正方形的边长是5cm时,它的周长是 ,面积是 。
7、如图,在正方形ABCD中,对角线AC与BD相交于O点,,则,正方形ABCD的周长是 ,正方形的面积是 。
8、已知正方形ABCD的一条对角线,则它的边长是 ,周长是 。
9、已知正方形的两条对角线的和为8cm,则它的边长为 ,面积为 。
10、(1)已知正方形的对角线长是cm,则它的边长是_____cm
(2)已知正方形的边长是cm,则它的对角线长是_____cm
11、在下列图中,有多少个正方形?有多少个矩形?
四、学习体会
五、课后学效检测与拓展
如图,在正方形ABCD是,E为对角线AC上一点,连结EB、ED。
(1)求证:△BEC≌△DEC。
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数。
18.2.3正方形的判定(第11课时)
学生信息班级 姓名
学习目标:1、掌握正方形的判定方法;2、能利用正方形的判定方法解决实际问题。
学习重点:掌握正方形的不同判定方法。
学习难点:正方形不同判定方法在实际中的应用。
一、温故知新
正方形的性质:
边:_________________________
角:_________________________
对角线:_______________________
二、自主学习
1、根据正方形既具有____________的特征,也具有____________的特征,我们可以得出正方形有如下判定方法:
①____________________的矩形是正方形。②__________________的菱形是正方形。
③对角线_____________的矩形是正方形。④对角线______________的菱形是正方形。
正方形的判定方法:
(1)矩形+ ______??????????????? 正方形
(2)菱形+ ______ 正方形
注:判定正方形的一般顺序:先证明它是平行四边形→再证明它是菱形(或矩形)→最后证明它是正方形。
三、合作探究
1、下列说法中错误的是( )
A、对角线相等的菱形是正方形 B、有一组邻边相等的矩形是正方形
C、四条边都相等的四边形是正方法 D、有一个角为直角的菱形是正方形
2、已知四边形两对角线:①互相垂直;②相等;③互相平分。具备条件____可得平行四边形;具备条件_______可得矩形;具备条件_______ 可得是菱形;具备条件________可得正方形。(填序号)
3、已知四边形ABCD是菱形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
4、在Rt△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别是E,F。
求证:(1)四边形CFDE是平行四边形。
(2)四边形CFDE是矩形或菱形(任选一项)。
(3)四边形CFDE是正方形。
四、随堂练习
1、判断下列命题是真命题还是假命题?假命题请举出反例。
(1)四条边相等且四个角也相等的四边形是正方形;( )
反例:
(2)四个角相等且对角线互相垂直的四边形是正方形;( )
反例:
(3)对角线互相垂直平分的四边形是正方形;( )
反例:
(4)对角线互相垂直且相等的四边形是正方形;( )
反例:
2、如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.求证: 四边形CFDE是正方形.
证明:
2、如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证: 四边形CFDE是正方形.
五、学习体会
六、课后学效检测与拓展
3、如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F。求证:四边形ABEF是正方形。
C
B
A
D
矩形
( )
平行四边形
6.
A
B
C
D
O
第8题
小结:判定一个图形是矩形的方法:
(1)平行四边形+ 矩形
(2)平行四边形+ 矩形
(3)四边形+ 矩形
( )
菱形
平行四边形
注:菱形是 的平行四边形。
A
B
C
D
O
A
B
C
D
O
A
C
B
D
小结:判定一个图形是菱形的方法:
(1)平行四边形+ 菱形
(2)平行四边形+ 菱形
(3) 的四边形 菱形
正方形
菱形
平行四边形
矩形
A
B
C
D
A
B
C
D
E
A
D
B
C
O
第5、7题
正方形分别有 ;
矩形分别有 。
A
B
C
D
E
F
A
B
C
D
E
F
PAGE
18.1.1平行四边形及性质(1)(第1课时)
学生信息班级 姓名
学习目标:1、掌握平行四边形的概念和对边相等对角相等的性质,根据概念和性质进行有关的计算和证明.
2、让学生学会用分析法和综合法解决问题
学习重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
学习难点:运用平行四边形的性质进行有关的论证和计算.
一、学前准备
1、定义:两组对边分别 的四边形叫平行四边形。
2、表示:平行四边形ABCD记作
二、合作探究
1.平行四边形的性质1:
边的性质:AB∥ ; BC∥
AB= ; BC=
即:平行四边形对边平行且 。
2.平行四边形的性质2: 角的性质:∠A= ,∠B=
即:平行四边形对角 。
3.平行四边形的性质:几何语言描述平行四边形的性质,
①∵四边形ABCD是平行四边形
∴ AB∥ ,AD∥
∴ AB = , AD =
②∵四边形ABCD是平行四边形
∴ ∠A=∠ , ∠B=∠
③∵四边形ABCD是平行四边形
∴AB∥CD,∴∠A与∠D互为邻补角,
∠A+∠D= , ∠B+∠C=
三、随堂练习
1、在 ABCD中,AB=3㎝,AD=5㎝,∠A=43°,∠B=137°,则DC= ,AD=
∠C= ,∠D= .其周长为 。
2、在?ABCD中∠A:∠B=4:5 ,那么∠C= ,∠D=_______.
3.已知?ABCD中,∠A比∠B小20°,则∠D的度数是( )
A.60° B.80° C.100° D.120°
4.在ABCD中,已知∠B=40,求其他各个内角的度数。
四、学习体会
五、课后学效检测与拓展
5.如图,在平行四边形ABCD中,CE⊥AB,AF⊥CD,垂足分别为E, F.求证:AF=CE.
4、如图,在 ABCD中,若,求和的度数。
5、如图,在平行四边形ABCD中,DF=BE,求证:AF=CE
18.1.1.2 平行四边形的性质(2)(第2课时)
学生信息班级 姓名
学习目标:1、掌握平行四边形的性质:平行四边形的对角线互相平分。
2、会运用平行四边形的性质进行推理和计算。
学习重点:平行四边形对角线互相平分的性质,以及性质的应用.
学习难点:综合运用平行四边形的性质进行有关的论证和计算.
一、学前准备
① 的四边形叫做平行四边形。
②平行四边形对边平行且 ;平行四边形对角 。
③两条平行线之间的任何两条平行线段都 。
二、合作探究
1.平行四边形的性质3:对角线的性质
已知:如图,?ABCD中,对角线AC和BD相交于点O,求证:OA=OC,OB=OD。
证明: ∵?ABCD是平行四边形
∴ ∥ ; = ;
∴∠ =∠ ,
在△ 和△ 中,
∴△ ≌△
∴
即平行四边形的对角线互相平分。
用几何语言
∵四边形ABCD是平行四边形
∴AO= = , BO= = ,
三、随堂练习
1、判断对错
(1)在ABCD中,AC交BD于O,则AO=OB=OC=OD. ( )
(2)平行四边形两条对角线的交点到一组对边的距离相等.( )
(3)平行四边形的两组对边分别平行且相等. ( )
(4)平行四边形是轴对称图形. ( )
2、如图,已知AB=5㎝,AD=8㎝,AC=6㎝, BD=12㎝,则AO= = ㎝,BO= = ㎝,△AOB的周长是 ㎝
3、平行四边形的对角线把平行四边形分成了 对全等的三角形。
4、在 ABCD中,两条对角线AC、BD相交于点O,指出图形中所有相等的线段。
5.如图,在ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为20,AB=8,那么对角线AC与BD的和是多少?
解:∵△AOB的周长为20(已知)
∴ + +AB=20,
∵AB=8
∴AO+BO=
∵在ABCD中,
∴AO = = ,,BO= = ,(平行四边形对角线 )
∴AC+BD = 2 +2 =2( )=
答:对角线AC和BD的和是 。
四、学习体会
五、课后学效检测与拓展
1、已知四边形ABCD是平行四边形,AB=5cm,BC=4cm,AC⊥BC,求BC、CD、AC、OA的长以及ABCD的面积.
2、如图,在ABCD中,BC=10,AC=8,BD=14.△AOD的周长为多少?△ABC与△DBC的周长哪个长?长多少?
18.1.2.1平行四边形的判定(1)(第3课时)
学生信息班级 姓名
学习目标:1、明确平行四边形的判定方法。
2、能运用平行四边形的判定,解决简单的实际问题。
学习重点:平行四边形的判定方法及应用.
学习难点:平行四边形的判定定理与性质定理的灵活应用.
一、学前准备
1、平行四边形的定义:
两组对边分别 的四边形叫做平行四边形。
-------定义就是平行四边形的一种判定方法
用几何语言表示:∵_________//___________
_________//____________
∴四边形ABCD是____________
2、平行四边形的性质:
(1)边的性质:平行四边形的对边 ;
几何语言:在 ABCD中,AD BC,AB DC;
(2)角的性质:平行四边形的对角 ;
几何语言:在ABCD中,∠A= ,∠B= ;
(3)对角线的性质:平行四边形的对角线 ;
几何语言:在ABCD中,OA= = ;OB= = ;
二、合作探究
已知:四边形ABCD, AB=CD,AD=BC求证:四边形ABCD是平行四边形
证明:连结AC,
在△ABC和△CDA中
归纳:判定定理一:两组对边分别相等的四边形是平行四边形
用几何语言表示:∵_________=___________
_________=____________
∴四边形ABCD是____________
2、类似地,我们还可以得出几个平行四边形的判定定理:
判定定理二:两组对角分别相等的四边形是平行四边形
用几何语言表示:∵∠_________=∠___________
∠_________=∠____________
∴四边形ABCD是____________
判定定理三:对角线互相平分的四边形是平行四边形
用几何语言表示:∵_________=___________
_________=____________
∴四边形ABCD是____________
三、随堂练习
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等 (B)两条对角线互相平分
(C)两条对角线相等 (D)两组对边分别平行
2、四边形ABCD中,AB∥CD,当满足下列哪个条件时,四边形ABCD是平行四边形( )
(A)∠B+∠C=180° (B) ∠A+∠B=180° (C) ∠A+∠D=180° (D) ∠A+∠C=180°
3、在四边形ABCD中,若∠B=∠D,那么再添加一个条件:____________,就可以判定ABCD是平行四边形。
4、如右图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=___ _cm,
CD=___ _cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=__ _cm,
DO=__ _cm时,四边形ABCD为平行四边形.
四、学习体会
五、课后学效检测与拓展
1、如图,在平行四边形ABCD中,E、F、G、H分别是各边中点。
求证:四边形EFGH是平行四边形。
2、如图,平行四边形ABCD的对角线AC,BD相交于点O,点 E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形
18.1.2.2平行四边形的判定(2)(第4课时)
学生信息班级 姓名
学习目标:1、掌握用一组对边平行且相等来判定平行四边形的方法
2、理解和领会三角形三角形中位线定理及其应用
3、会综合应用平行四边形的四种判定方法和性质来证明问题
学习重点:平行四边形各种判定方法及其应用,尤其是根据不同条件能正确地选择判定方法.
学习难点:平行四边形的判定定理与性质定理的综合应用.
一、自主学习
1、判定平行四边形的方法有哪几个:①
② ③ 。
2、预习课本第46—49页
3、如右图所示,△ABC各边的中点分别是D、E、F,则在△ABC中,中位线有那几条:
二、合作探究
1、已知:四边形ABCD, AB∥CD,AB=CD,求证:四边形ABCD是平行四边形
证明:连结AC,
总结:平行四边形的判定定理:
2、点D、E分别是△ABC的边AB、AC的中点,求证:DE∥BC、DE=.
总结:三角形的中位线定理:
三、随堂练习
1、判断题:
(1)一组对边平行,另一组对边相等的四边形是平行四边形; ( )
(2)对角线互相平分的四边形是平行四边形. ( )
(3)两组对角分别相等的四边形是平行四边形; ( )
2、已知一个三角形的三边长分别为5㎝,7cm,8㎝,则连接各边中点所形成的三角形的周长为 cm。
3、三角形的一条中位线分三角形所形成的新三角形与原三角形的周长之和为60㎝,则原三角形的周长为 cm。
4、如图,△ABC中,DE是△ABC的中位线、F是BC的中点,
(1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm;
(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.
5、已知:如图,ABCD中,E、F分别是AC上两点,BE∥DF,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
四、学习体会
五、课后学效检测与拓展
已知:如图2、已知:如图(1),在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
18.2.1矩形的性质(第5课时)
学生信息班级 姓名
学习目标:1、了解矩形与平行四边形的关系;
2、初步认识矩形性质。
3.直角三角形斜边上的中线的性质,并能运用相关性质求解。
学习重点:矩形的性质.
学习难点:矩形的性质的灵活应用.
一、学前准备
1、①四边形ABCD是平行四边形 的三个性质:
②四边形ABCD的判定定理
③ 连接三角形两边中点的线段叫做 ,三角形的中位线平行于 ,并且等于第三边的 。
2、预习课本第52—53页
二、合作探究
1、矩形的定义:
2.矩形的性质:(在旁边的空白处画一个矩形并通过观察或度量进行归纳)
(1)边: ;
(2)角: ;
(3)对角线: 。
归纳:(几何语言)
平行四边形 矩形
图形
边 AB∥DC,AD∥ ,AB=DC,AD BC AB∥ ,AD∥ ,AB=DC,AD BC
角
对角线
小结1.:矩形是 的平行四边形
小结2.:矩形的两条对角线 。
3、观察下面三个图形,你能从中看到什么?
AO=BO= = = =
BO是斜边 上的 线。BO= = =
结论:直角三角形斜边上的中线等于 的一半。
三、随堂练习
1.矩形ABCD的对角线,则另一条对角线。
2.矩形的定义中有两个条件:一是 ,二是 .
3.直角三角形斜边上的中线长时8㎝,则斜边是 ㎝ 。
4.已知矩形ABCD,AC=8,则BD= ,OD= 。
5.已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
6.矩形不一定具有的性质是( )
A、对角线相等 B、四个角相等 C、是轴对称图形 D、对角线互相垂直
7.已知矩形的周长是24cm,相邻两边之比是,那么这个矩形的边长分别是 。
8.如图,已知矩形ABCD,AC=4,则BD= ,∠ABC= ;若∠ADB=40°,则∠ACB= °,
∠BDC= °,∠COD= °。
四、学习体会
五、课后学效检测与拓展
如图,在矩形ABCD中,E是CD上的一点,,且,
求的度数。
18.2.1矩形的判定(第6课时)
学生信息班级 姓名
学习目标:1、掌握矩形的判定方法。
2、能运用矩形的判定方法解决有关问题。
学习重点:矩形的判定.
学习难点:矩形的判定及性质的综合应用.
一、学前准备
1.矩形的性质:(1)对边 且 。(2)四个角都是 。(3)对角线 且 。
2.已知一个矩形的长时2cm,宽是1cm,它的对角线长是 。
3.在矩形ABCD中,AB=3,AC=5,则BC= ,这个矩形的面积是 。
二、合作探究(教材p54页)
1、定义:有一个角是 的平行四边形是矩形。
几何语言,如图∵ ABCD中,∠A= °,
∴ ABCD是
2、对角线相等的平行四边形是矩形。
几何语言:如图∵ ABCD中,______=_______
∴ ABCD是 。
3、有三个角是直角的四边形是矩形。
几何语言:如图 在四边形ABCD中
∵∠ =∠ =∠ = °
∴四边形ABCD是 。
如图,在ABCD中,对角线AC,BD相较于点OB=OC,∠OBA=60°.求∠OBC的度数。
三、随堂练习
1、如右图,已知四边形ABCD中,OA=OB=OC=OD=5cm,
则四边形ABCD是 。理由: 。
2.ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,且AB=4,则ABCD是 形,则它的面积是 。
3.下列说法中,不能判定四边形是矩形的是( )
A 对角线相等的平行四边形 B 对角线互相平分的四边形
C 四个角都相等的四边形 D 有一个角等于90°的平行四边形
4、如图,中,AB=6,BC=8,AC=10,求证:四边形ABCD是矩形
四、学习体会
五、课后学效检测与拓展
1、如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2,它是一个矩形吗?为什么?
2.已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形。
18.2.2菱形的性质(第7课时)
学生信息班级 姓名
学习目标:1、了解菱形与平行四边形的关系; 2、初步认识菱形的特征。
学习重点::菱形的性质.
学习难点:菱形的性质及菱形知识的综合应用.
一、学前准备
如图,在中,
①∵四边形ABCD是平行四边形
∴ AB∥ ,AD∥
AB = , AD =
②∵四边形ABCD是平行四边形
∴ ∠A=∠ , ∠B=∠
③∵四边形ABCD是平行四边形
∴AO= = , BO= = ,
二、合作探究
1、菱形的定义:
2.菱形的特征:(在旁边的空白处画一个菱形并通过观察或度量进行归纳)
(1)边: ;
(2)角: ;
(3)对角线: 。
平行四边形 菱形
图形
边 AB∥DC,AD∥ AB=DC,AD BC AB∥ ,AD∥
角
对角线
已知菱形ABCD的边长为40cm,,对角线AC、BD相交于点O,求这个菱形的两条对角线AC与BD的长。以及菱形ABCD的面积。(参考教材56页例3)
三、随堂练习
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4,则AC= .BD=
2.已知菱形ABCD的对角线AC与BD相交于点O,请说明菱形ABCD的面积等于。
解:菱形ABCD
,
= =
小结:菱形的面积等于两条对角线
3、在菱形ABCD中,∠BAD=60°,则∠ADC= °,∠DCA= °,
∠BAC= °,∠ADB= ,∠CBD= °
4、如图,在菱形ABCD中,,两条对角线相交于点O,若,,AB= 对角线,则菱形的周长是 ,面积是 。
四、学习体会
五、课后学效检测与拓展
1、已知菱形ABCD的边长为5cm,对角线AC长6cm,则另一条对角线BD长为 cm,菱形的面积为:
2、如图,在菱形ABCD中,∠BAD=2∠B,试说明△ABC是等边三角形。
18.2.2菱形的判定(第8课时)
学生信息班级 姓名
学习目标:1、掌握菱形的判定方法;2、能运用菱形的判定方法解决有关问题。
学习重点:菱形的两个判定方法.
学习难点:判定方法的证明方法及运用.
一、复习回顾:
(1)菱形的定义: ;
(2)菱形的性质1 : ;
性质2 : ;
(3)菱形的特征
A:对边 ________,四条边都 。
B:对角 。
C:两条对角线互相 ,并且每一条对角线平分 。
(4)菱形的面积等于两条对角线 。
二、自主学习(预习p57-58页)
1、菱形的识别:
方法一:有一组邻边 的平行四边形是菱形。(定义)
几何语言:∵ ABCD中,AB=
∴ ABCD是 。
方法二:对角线互相垂直的平行四边形是菱形
(即:平行四边形+对角线 菱形
几何语言:如图∵ ABCD中,______⊥_______
∴ ABCD是 。
方法三: 四条边都 的四边形是菱形。
几何语言:∵四边形ABCD中,AB BC CD DA
∴四边形ABCD是菱形。
三、合作探究
例题1:如图 ABCD的对角线AC,BD相交于点O,且AB=10,AO=8,BO=6.求证, ABCD是菱形。
例题2:在中,对角线AC平分∠DAB,这个四边形是菱形吗?简述理由
四、随堂练习
1.在中,若一条对角线平分一个内角,这个平行四边形是 形。
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和6,是一个特殊的平行四边形吗?为什么?求出它的面积。
3.如图,AE//BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,
求证:四边形ABCD是菱形。
五、学习体会
六、课后学效检测与拓展
1、已知四边形ABCD是平行四边形,请补充一个条件 ,使四边形ABCD成为菱形
2、如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证四边形AFCE是菱形.
证明:
18.2.3正方形的性质(第9课时)
学生信息班级 姓名
学习目标:1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别。
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
一、学前准备
(预习教材p58-59页)
二、合作探究
1、有一组_______相等并且有一个角是________的平行四边形叫做正方形。有一个角是________的菱形叫做正方形;一组________相等的矩形叫做正方形。
2、正方形既是_____,又是_____,所以它具有_____ 和 _____ 的性质:
(1)正方形的四个角都是_____ ,四条边都 _____ ;
(2)正方形的对角线_____且 ________,每条对角线平分__________;
(3)正方形是_______图形,____________的交点是它的对称中心;
(4)正方形是_______图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴。
3、见教材P59图18.2-12,正方形ABCD的对角线把它分成了____个三角形,它们是_____三角形,它们全等吗?请简单说明
理由____________________________________________________。
三、随堂练习
1、下列正方形具有而一般菱形不具有的性质是 ( )
A. 四条边都相等 B. 对角线互相垂直平分 C. 对角线相等 D. 每一条对角线平分一组对角
2、正方形具有而一般矩形不一定具有的性质是 ( )
A. 四个角相等 B. 四条边相等 C. 对角线互相平分 D. 对角线相等
3、已知一个正方形的边长为2cm,则对角线长为______。
4、已知一正方形的对角线长为2cm,则它的边长为_______。
5、若正方形的一条对角线长为4cm,则正方形的周长为______,面积为________;
对角线的交点到边的距离为_______。
6、顺次连接正方形各边中点,得4个等腰直角三角形,则每个小三角形的面积为原正方形面积的 ______ 。
7、如图,四边形ABCD是正方形,∠CAB是多少度?为什么?至少用两种方法说明理由。
四、学习体会
五、课后学效检测与拓展
1、正方形是轴对称图形,它的对称轴有____条,正方形也中心对称图形,它的对称中心是________。
2如图,在正方形ABCD中,∠DAE=25°,AE交对角线BD于E点,
那么∠BEC等于( )
A、45° B、60° C、70° D、75°
3、如图,E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD与∠ECD的度数.
4、如图,点E是正方形ABCD边CD上的一点,点F是CB和延长线上的点,且EAAF。
求证:DE=BF。
18.2.3正方形的性质(2)(第10课时)
学生信息班级 姓名
学习目标:1、了解正方形与平行四边形的关系;2、认识正方形的特征。
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
一、自主学习
1、正方形的定义:
矩形是 的平行四边形,菱形是 平行四边形
而:有一个角是直角,且有一组邻边相等的 是正方形。
2、正方形的性质:(在旁边空白处画一个正方形,并能过观察或度量归纳正方形的特征)
(1)边:
(2)角:
(3)对角线:
二、合作探究(小组交流合作并展示归纳)
平行四边形 矩形 菱形 正方形
图形
边 AB∥DC,AD∥ AB=DC,AD BC AB∥ ,AD∥ AB=DC,AD BC AB∥ ,AD∥ AB∥ ,AD∥
角
对角线 (1) (1) (2) (3)一条对角线平分一组对角 (1)(3)(同菱形)
注:矩形,菱形,正方形都是 的平行四边形。
三、随堂练习
1、正方形具有而菱形不一定具有的性质是( )
A 对角线互相平分 C 对角线相等
B 内角和为360? D 对角线平分内角
2、正方形具备而矩形不一定具备的性质是( )
A 四个角都是直角 C 四条边相等
B 对角线相等 D 对角线互相平分
3、下列说法错误的是( )
A 正方形的四条边相等 B 正方形的四个角相等
C 平行四边形对角线互相垂直 D 正方形的对角线相等
4、在正方形ABCD中,AO=5,则BO= ,BD= ;∠ABC= °
5、如图,在正方形ABCD中,对角线AC与BD相交于点O,则
,,。
6、正方形的边长是5cm时,它的周长是 ,面积是 。
7、如图,在正方形ABCD中,对角线AC与BD相交于O点,,则,正方形ABCD的周长是 ,正方形的面积是 。
8、已知正方形ABCD的一条对角线,则它的边长是 ,周长是 。
9、已知正方形的两条对角线的和为8cm,则它的边长为 ,面积为 。
10、(1)已知正方形的对角线长是cm,则它的边长是_____cm
(2)已知正方形的边长是cm,则它的对角线长是_____cm
11、在下列图中,有多少个正方形?有多少个矩形?
四、学习体会
五、课后学效检测与拓展
如图,在正方形ABCD是,E为对角线AC上一点,连结EB、ED。
(1)求证:△BEC≌△DEC。
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数。
18.2.3正方形的判定(第11课时)
学生信息班级 姓名
学习目标:1、掌握正方形的判定方法;2、能利用正方形的判定方法解决实际问题。
学习重点:掌握正方形的不同判定方法。
学习难点:正方形不同判定方法在实际中的应用。
一、温故知新
正方形的性质:
边:_________________________
角:_________________________
对角线:_______________________
二、自主学习
1、根据正方形既具有____________的特征,也具有____________的特征,我们可以得出正方形有如下判定方法:
①____________________的矩形是正方形。②__________________的菱形是正方形。
③对角线_____________的矩形是正方形。④对角线______________的菱形是正方形。
正方形的判定方法:
(1)矩形+ ______??????????????? 正方形
(2)菱形+ ______ 正方形
注:判定正方形的一般顺序:先证明它是平行四边形→再证明它是菱形(或矩形)→最后证明它是正方形。
三、合作探究
1、下列说法中错误的是( )
A、对角线相等的菱形是正方形 B、有一组邻边相等的矩形是正方形
C、四条边都相等的四边形是正方法 D、有一个角为直角的菱形是正方形
2、已知四边形两对角线:①互相垂直;②相等;③互相平分。具备条件____可得平行四边形;具备条件_______可得矩形;具备条件_______ 可得是菱形;具备条件________可得正方形。(填序号)
3、已知四边形ABCD是菱形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
4、在Rt△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别是E,F。
求证:(1)四边形CFDE是平行四边形。
(2)四边形CFDE是矩形或菱形(任选一项)。
(3)四边形CFDE是正方形。
四、随堂练习
1、判断下列命题是真命题还是假命题?假命题请举出反例。
(1)四条边相等且四个角也相等的四边形是正方形;( )
反例:
(2)四个角相等且对角线互相垂直的四边形是正方形;( )
反例:
(3)对角线互相垂直平分的四边形是正方形;( )
反例:
(4)对角线互相垂直且相等的四边形是正方形;( )
反例:
2、如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.求证: 四边形CFDE是正方形.
证明:
2、如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证: 四边形CFDE是正方形.
五、学习体会
六、课后学效检测与拓展
3、如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F。求证:四边形ABEF是正方形。
C
B
A
D
矩形
( )
平行四边形
6.
A
B
C
D
O
第8题
小结:判定一个图形是矩形的方法:
(1)平行四边形+ 矩形
(2)平行四边形+ 矩形
(3)四边形+ 矩形
( )
菱形
平行四边形
注:菱形是 的平行四边形。
A
B
C
D
O
A
B
C
D
O
A
C
B
D
小结:判定一个图形是菱形的方法:
(1)平行四边形+ 菱形
(2)平行四边形+ 菱形
(3) 的四边形 菱形
正方形
菱形
平行四边形
矩形
A
B
C
D
A
B
C
D
E
A
D
B
C
O
第5、7题
正方形分别有 ;
矩形分别有 。
A
B
C
D
E
F
A
B
C
D
E
F
PAGE
