2020春华师版九下数学第26章二次函数复习课件(78张PPT)
文档属性
| 名称 | 2020春华师版九下数学第26章二次函数复习课件(78张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 970.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 18:40:54 | ||
图片预览










文档简介
(共78张PPT)
第26章
单元复习课
一、二次函数的概念
1.定义
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
2.由二次函数的定义可知二次函数必须满足三个条件:
(1)函数关系式是整式;
(2)化简后自变量的最高次数必须是2;
(3)二次项的系数不为0,一次项系数b和常数项c可以为任意实
数.
3.二次函数定义的应用
与二次函数定义有关的问题的应用有两个方面,解题的关键是
理解二次函数的概念:
一是根据定义判断函数的类型,在判断时要先把函数化成一般
形式,再严格按照定义,对含有字母系数的二次函数,着重看
二次项的系数是否为零;
二是根据二次函数的定义,求某些字母的取值范围,解题的关
键是根据次数构建关于所求字母的方程,然后求解.
注:(1)利用二次函数的定义解题时,尤其是含有字母系数的
函数,应特别留意二次项的系数是否为0.
(2)根据实际问题列函数关系式时,要注意自变量的取值范围
需保证使实际问题有意义.
二、二次函数的图象及其性质
1.二次函数y=ax2的图象及其性质
(1)抛物线y=ax2的顶点是坐标原点,对称轴是y轴.
(2)①当a>0时,图象位于x轴的上方,抛物线开口向上,顶点为
其最低点;在对称轴的左侧,y随x的增大而减小,在对称轴的
右侧,y随x的增大而增大;
②当a<0时,图象位于x轴的下方,抛物线开口向下,顶点为其最
高点;在对称轴的左侧,y随x的增大而增大,在对称轴的右
侧,y随x的增大而减小;
(3)①当a>0时,函数y=ax2有最小值,最小值是0;
②当a<0时,函数y=ax2有最大值,最大值是0.
注:应用函数图象及其性质时,要注意数与形的有机结合,特
别是利用函数的图象解决问题时,需充分考虑抛物线的对称性.
2.二次函数y=ax2+bx+c的图象及其性质
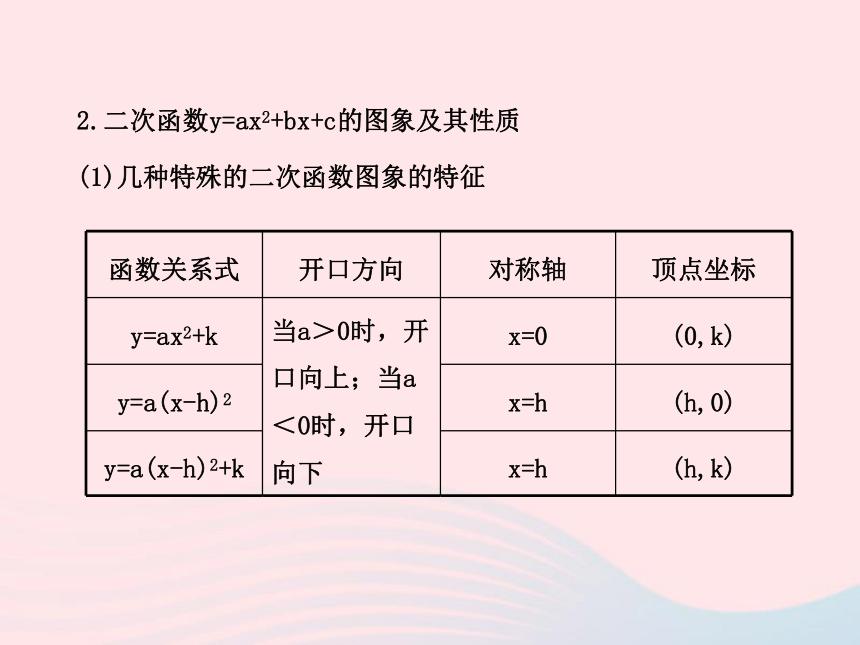
(1)几种特殊的二次函数图象的特征
函数关系式
开口方向
对称轴
顶点坐标
y=ax2+k
当a>0时,开口向上;当a<0时,开口向下
x=0
(0,k)
y=a(x-h)2
x=h
(h,0)
y=a(x-h)2+k
x=h
(h,k)
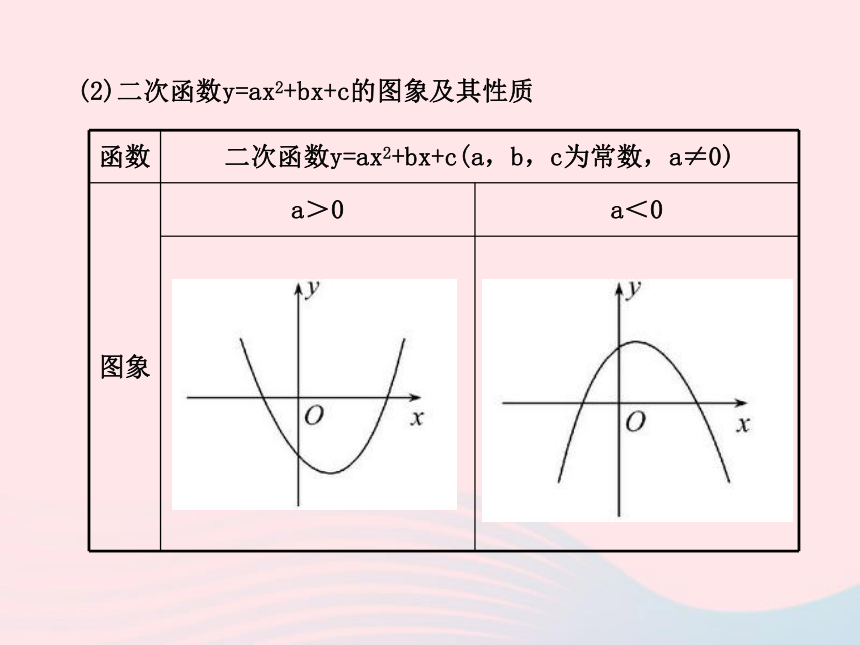
(2)二次函数y=ax2+bx+c的图象及其性质
函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
图象
a>0
a<0
函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
性质
①抛物线开口向上
①抛物线开口向下
②对称轴是直线
顶点是
③当x<
时,y随x的
增大而减小;当x>
时,y随x的增大而增大
③当x<
时,y随x的
增大而增大;当x>
时,y随x的增大而减小
④抛物线有最低点,当
x=
时,y有最小值,
y最小值=
④抛物线有最高点,当
x=
时,y有最大值,
y最大值=
3.系数a,b,c与二次函数的图象
(1)a决定开口方向及开口大小
当a>0时,开口向上,当a<0时,开口向下;|a|越大,抛物
线的开口越小;
(2)b和a共同决定抛物线对称轴的位置
由于抛物线y=ax2+bx+c(a≠0)的对称轴是直线
故:
①b=0时,对称轴为y轴;
②
>0(即a,b同号)时,对称轴在y轴左侧;
③
<0(即a,b异号)时,对称轴在y轴右侧.
(3)c的大小决定抛物线y=ax2+bx+c与y轴交点的位置
当x=0时,y=c,∴抛物线y=ax2+bx+c与y轴有且只有一个交点
(0,c).即①c=0,抛物线经过原点;②c>0,与y轴交于正半轴;
③c<0,与y轴交于负半轴.
以上三点中,当结论和条件互换时,仍成立.
4.二次函数图象的平移规律
平移不改变图形的形状和大小,因此抛物线在平移的过程中,
图象的形状、开口方向必相同,即a不变,所以抛物线
y=ax2+bx+c可以由y=ax2平移得到.其平移的规律用语言来表示
可以归结为:“上加下减,左加右减”,平移时具体的对应关
系可以用下列框图来表示:
三、二次函数的相关计算
1.求抛物线的顶点、对称轴的方法:
(1)公式法:
∴顶点是
,对称轴是直线
(2)配方法:运用配方的方法,将抛物线的关系式化为
y=a(x-h)2+k的形式,得到顶点为(h,k),对称轴是直线x=h.将
关系式y=ax2+bx+c化为y=a(x-h)2+k的形式,其基本步骤是:
①提取二次项的系数,把二次项的系数化为1(注意与一元二次
方程中配方法的区别);
②对上面的二次函数的二次三项式配方,即加上一次项系数一
半的平方,配方时不能改变原式的值;
③写成y=a(x-h)2+k的形式.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称
图形,所以对称的两点的连线的垂直平分线是抛物线的对称
轴,对称轴与抛物线的交点是顶点.
若已知抛物线上两点
(x1,y)、(x2,y),则对称轴方程可以表示为:
2.求二次函数关系式
(1)二次函数关系式常用的有三种形式
①一般式:y=ax2+bx+c(a≠0);
②顶点式:y=a(x-h)2+k(a≠0)
;
③交点式:y=a(x-x1)(x-x2)(a≠0).
(2)恰当地选择二次函数的表达形式求关系式
求解二次函数关系式一般用待定系数法,根据所给条件的不
同,要灵活选用函数关系式的表达形式:
①当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+
c(a≠0)的形式,然后组成三元一次方程组来求解.
②当已知抛物线的顶点或对称轴或最大(小)值时,通常设为顶
点式y=a(x-h)2+k(a≠0)的形式.
③当已知抛物线与x轴的交点(或交点横坐标)或已知抛物线与x
轴一个交点和对称轴时,通常设为交点式:y=a(x-x1)(x-
x2)(a≠0).
注:(1)用待定系数法求解二次函数的关系式,题目给出的方式
比较灵活,除上述三种方式外,往往还结合函数的性质提供一
些条件.如
①抛物线的形状相同(形状相同的两个抛物线的二次项的系数相
同或互为相反数,在解题时要注意,防止漏解);
②与坐标轴的交点坐标所围成的三角形的面积;
③依据函数增减性,通过增减性的不同确定抛物线的对称轴,
再设为顶点式求解;
④结合函数的图象平移给出某些点的坐标;
⑤应用函数图象与x轴的交点与一元二次方程的关系,借助方程
的解给出条件.
(2)不论应用何种形式设关系式,最后求得的结果一般化为一般
形式.
(3)当题目条件中点的条件不足三个时,要充分利用二次函数的
对称性转化条件.
四、二次函数与一元二次方程的关系
1.二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)
的关系
(1)“数”的角度:当二次函数y=ax2+bx+c(a≠0)的函数值等于
0时,相应的自变量的值即为一元二次方程ax2+bx+c=0(a≠0)的
解.
(2)“形”的角度:若抛物线y=ax2+bx+c(a≠0)与x轴两交点为
A(x1,0),B(x2,0),则一元二次方程ax2+bx+c=0(a≠0)的两个根
为x1,x2.
2.抛物线与x轴的交点情况与一元二次方程的根的判别式的关
系:
(1)有两个交点 b2-4ac>0;
(2)有一个交点(顶点在x轴上) b2-4ac=0;
(3)没有交点 b2-4ac<0.
注:根据抛物线的开口方向和顶点的位置也可以判断抛物线与x
轴的交点个数,如a>0,顶点在x轴的上方,则抛物线与x轴没
有交点.
3.应用二次函数图象求方程的近似根的步骤
(1)根据方程确定与方程有关的二次函数;
(2)画出二次函数的图象;
(3)初步估值,确定一元二次方程的根的取值范围,即确定抛物
线与x轴交点的横坐标的大体范围;
(4)在初步估值确定的范围内,从小到大或从大到小依次取值,
借助计算器探索,确定近似值.
4.直线与抛物线的交点
(1)y轴与抛物线y=ax2+bx+c的交点为(0,c).
(2)与y轴平行的直线x=h与抛物线y=ax2+bx+c有且只有一个交点
(h,ah2+bh+c).
(3)抛物线与x轴的交点
二次函数y=ax2+bx+c的图象与x轴的两个交点的横坐标x1,x2,
是对应的一元二次方程ax2+bx+c=0的两个实数根.抛物线与x轴
的交点情况可以由对应的一元二次方程的根的判别式判定.
(4)平行于x轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点
时,两交点的纵坐标相等,设纵坐标为k,则横坐标是
ax2+bx+c=k的两个实数根.
(5)一次函数y=kx+n(k≠0)的图象l与二次函数y=ax2+bx+c(a≠0)
的图象G的交点,由方程组
的解的数目来确定:
①方程组有两组不同的解 l与G有两个交点;②方程组只有一
组解 l与G只有一个交点;③方程组无解 l与G没有交点.
(6)抛物线与x轴两交点之间的距离:若抛物线y=ax2+bx+c与x轴
两交点为A(x1,0),B(x2,0),由于x1,x2是方程ax2+bx+c=0的两
个根,故x1+x2=
x1·x2=
五、应用二次函数解决实际问题
二次函数是反映现实世界中变量间的数量关系和变化规律的一
种常见的数学模型,它的应用体现的核心问题是数学建模思想
的应用,解题的关键是准确理解题意,建立合适的函数模型.解
决此类问题的基本思路是:(1)理解问题;(2)分析问题中的变
量和常量以及它们之间的关系;(3)用函数关系式表示它们之间
的关系;(4)计算或求解,并应用函数的性质作出判断;(5)检
验结果的合理性.
注:1.不能选择恰当的函数关系式表示实际问题中的数量关系;
2.利用二次函数解决实际问题时,对题意理解不清,导致无法列出正确的函数关系式;
3.不考虑自变量的取值范围,所求最值与实际不符;
4.易把求最大值和最小值的公式与一元二次方程的求根公式相混.
实际问题
实际问题
的解决
二次函数
y=ax2+bx+c(a
0)
二次函数与一元
二次方程的关系
二次函数的
图象与性质
关系式
图
象
性
质
平移规律
二次函数的对称轴及顶点坐标
【相关链接】
确定二次函数对称轴及顶点坐标的两种方法
1.公式法:对称轴是直线
顶点坐标是
2.配方法:将二次函数通过配方化为y=a(x-h)2+k(a≠0)的形
式,对称轴为x=h,顶点坐标是(h,k).
【例1】已知二次函数y=2(x-3)2+1.下列说
法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其
图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小,则其
中说法正确的有(
)
(A)1个
(B)2个
(C)3个
(D)4个
【思路点拨】根据抛物线y=a(x-h)2+k(a≠0)的性质进行判断.
【自主解答】选A.∵2>0,∴图象的开口向上,故①错误;
图象的对称轴为直线x=3,故②错误;
其图象顶点坐标为(3,1),故③错误;
当x<3时,y随x的增大而减小,④正确.
综上所述,说法正确的有④,共1个.
确定函数关系式
【相关链接】
待定系数法主要用于确定二次函数的关系式
1.当已知抛物线上任意三点坐标时,可以通过设函数关系式为
一般式y=ax2+bx+c(a≠0)进行求解;
2.当已知抛物线顶点坐标、对称轴或最值时,可以通过设函数
关系式为y=a(x-h)2+k(a≠0)进行求解;
3.如果已知抛物线与x轴的两个交点(x1,0)(x2,0)时,可设为
交点式y=a(x-x1)(x-x2)进行求解.
【例2】如图,抛物线y=x2+bx+c经过坐标
原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且
S△OAB=3,求点B的坐标.
【思路点拨】(1)
(2)
(3)
【自主解答】(1)把(0,0),(2,0)代入y=x2+bx+c得
解得
所以解析式为y=x2-2x.
(2)∵y=x2-2x=(x-1)2-1,
∴顶点为(1,-1).
对称轴为直线x=1.
(3)设点B的坐标为(m,n),则
解得n=3或n=-3,
∵顶点纵坐标为-1,-3<-1(或x2-2x=-3中,x无解)
∴n=3,
∴x2-2x=3.
解得x1=3,x2=-1.
所以点B的坐标为(3,3)或(-1,3).
二次函数的图象与性质
【相关链接】
某些特殊形式的代数式的符号的判断:
(1)
a+b+c,即x=1时y的值.
(2)
b2-4ac,根据图象与x轴交点的个数判断.
系数的符号
图象特征
a的符号
开口向上 a>0,开口向下 a<0
b的符号
左同右异,顶点在y轴左侧,b与a符号相同;顶点在y轴右侧,b与a符号相异.
c的符号
c为图象与y轴交点的纵坐标
【例3】已知二次函数y=ax2+bx+c(a≠0)的图
象如图所示,现有下列结论:①
b2-4ac>0;②
a>0;③
b>
0;④
c>0;⑤9a+3b+c<0,则其中结论正确的个数是(
)
(A)2个
(B)3个
(C)4个
(D)5个
【思路点拨】根据函数图象中抛物线的开口方向判断a的符号,
再结合对称轴的位置判断b的符号;根据抛物线与y轴交点的位
置判断c的符号;根据抛物线与x轴交点的个数判断b2-4ac的符
号;根据对称轴x=1,可判断(3,0)的对称点为(-1,0),由x=-1时
的y值的符号来判断9a+3b+c的符号.
【自主解答】选B.①根据图象知,二次函数与x轴有两个交点,
所以b2-4ac>0,∴①正确;
②根据图象知,该函数图象的开口向上,∴a>0,②正确;③又
对称轴
∴b<0,∴③错误;
④该函数图象交于y轴的负半轴,∴c<0,∴④错误;
⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称
点是(3,0);当x=-1时,y<0,所以当x=3时,也有y<0,
即9a+3b+c<0,⑤正确.所以①②⑤正确.
二次函数的应用
【相关链接】
在应用二次函数解决实际问题时,首先要注意对实际问题进行
观察分析,并从中抽象出相应的数量关系,建立二次函数模
型,进而利用二次函数的图象与性质解答.在解答时要注意实际
问题中数量及数量关系的意义要符合实际问题的要求和限制,特
别是自变量取值范围的限制及其对应的函数值的取值范围的要
求.
【例4】许多家庭
以燃气作为烧水做饭的燃料,节约用
气是我们日常生活中非常现实的问
题,某款燃气灶旋钮位置从0度到90度
(如图),燃气关闭时,燃气灶旋钮的位
置为0度,旋钮角度越大,燃气流量越大,燃气开到最大时,旋钮角
度为90度.为测试燃气灶旋钮在不同位置上的燃气用量,在相同条
件下,选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋
旋钮角度(度)
20
50
70
80
90
所用燃气量(升)
73
67
83
97
115
钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度
的范围是18≤x≤90),记录相关数据得到下表:
(1)请你从所学习过的一次函数、反比例函数和二次函数中确定
哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律 说明
确定是这种函数而不是其他函数的理由,并求出它的关系式.
(2)当旋钮角度为多少时,烧开一壶水所用燃气量最少 最少是多
少
(3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最
节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭
以前每月的平均燃气用量.
【思路点拨】(1)根据列表中的相关数据,分别选取合适的点的
坐标求出一次函数、反比例函数和二次函数的关系式,再用另
外的点加以验证,得出结论.
(2)根据二次函数的性质,解决问题.
(3)根据题意,结合(1),(2)分析求出结果.
【自主解答】(1)若设y=kx+b(k≠0),由
解得
所以
把x=70代入得y=63≠83,所以不符合.
若设
由
解得k=1
460,
所以
把x=50代入得y=29.2≠67,所以不符合;
若设y=ax2+bx+c,则由
解得
所以
把x=80代入得y=97,把x=90代入得y=115,符合题意.
所以选用二次函数能表示所用燃气量y升与旋钮角度x度的变化
规律.
(2)由(1)得
所以当x=40时,y取得最小值65.
即当旋钮角度为40度时,烧开一壶水所用燃气量最少,最少为
65升.
(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开
到最大时烧开一壶水节约用燃气115-65=50(升),
设该家庭以前每月平均用燃气量为a立方米,则由题意得
解得a=23(立方米),
即该家庭以前每月平均用气量为23立方米.
【命题揭秘】
结合近几年中考试题分析,二次函数的内容考查主要有以下特
点:
1.命题方式为二次函数表达式的确定,二次函数的图象与性质
的应用,判定二次函数的顶点坐标、开口方向、对称轴方程,
用函数观点解决方程(组)、不等式问题;二次函数的实际应
用,题型多样,涉及选择题、填空题与解答题.
2.命题的热点为二次函数表达式的求法、二次函数的实际应
用,二次函数与一次函数、反比例函数的综合应用,以及函数
与方程(组)、不等式知识相融合的综合题目的考查.
1.下列二次函数中,图象以直线x=2为对称
轴、且经过点(0,1)的是(
)
(A)y=(x-2)2+1
(B)y=(x+2)2+1
(C)y=(x-2)2-3
(D)y=(x+2)2-3
【解析】选C.根据以直线x=2为对称轴可知选项A,C符合,再根据图象经过点(0,1)知选项C符合.
2.已知二次函数y=-x2+x-
,当自变量x取m时,
对应的函数值大于0,当自变量x分别取m-1,m+1时对应的函数值
为y1,y2,则必有y1,y2满足(
)
(A)y1>0,y2>0
(B)y1<0,y2<0
(C)y1<0,y2>0
(D)y1>0,y2<0
【解析】选B.∵
图象开口向下,与x
轴两交点都在0到1之间,由当自变量x取m时,对应的函数值大于0,
得0<m<1,∴-1<m-1<0,
1<m+1<2,根据图象可得y1<0,y2<0.
故选B.
3.竖直向上发射的小球
的高度h(m)关于运动时间t(s)的函数表达
式为h=at2+bt,其图象如图所示,若小球在
发射后第2秒与第6秒时的高度相等,则下列
时刻中小球的高度最高的是(
)
(A)第3秒
(B)第3.5秒
(C)第4.2秒
(D)第6.5秒
【解析】选C.由题意知,当t=4时小球的高度最高,当t=3与t=5时
小球高度相等,当t<4时,h随t的增大而增大;当t>4时,h随t的
增大而减小,∴四个选项中,当t=4.2时,小球高度最高.
4.如图是二次函数y=ax2+bx+c(a≠0)的图
象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c
=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是
__________
.(只要求填写正确命题的序号)
【解析】由图可知,当x=1时,y=0,即a+b+c=0;又对称轴为-1,
则
则b=2a;由抛物线的对称性可知,此二次函数与x轴
的另一个交点坐标为(-3,0),根据函数与方程的关系可知,方程
ax2+bx+c=0的两根分别为-3和1;由a+b+c=0得,a+c=-b,则
a-2b+c=-3b,因为a>0,则b=2a>0,所以a-2b+c=-3b<0,所以
①③正确.
答案:①③
5.如图,已知抛物线y=x2+bx+c经过点(0,
-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)
和(3,0)之间.你所确定的b的值是_________.
【解析】把点(0,-3)代入函数的关系式可得c=-3,只要是再把一
个点的坐标代入关系式就可求出b值.由“与x轴的一个交点在
(1,0)和(3,0)之间”可选择满足条件的点的坐标代入即可,如代
入(2,0)可求
答案:
(答案不唯一)
6.如图,已知函数
与y=ax2+bx(a>0,b>0)
的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+
=0
的解为__________.
【解析】∵P的纵坐标为1,
∴P的横坐标为-3.
∵
可化为关于x的方程ax2+bx=
的形式,
∴此方程的解即为两函数图象交点的横坐标的值,
∴x=-3.
答案:x=-3
7.已知:抛物线与直线
y=x+3分别交于x轴和y轴上同一点,交点分
别是点A和点C,且抛物线的对称轴为直线
x=-2.
(1)求出抛物线与x轴的两个交点A,B的
坐标;
(2)试确定抛物线的关系式;
(3)观察图象,请直接写出二次函数值小于一次函数值的自变量
x的取值范围.
【解析】(1)y=x+3中,
当y=0时,
x=-3,
∴点A的坐标为(-3,0).
当x=0时,y=3,
∴点C坐标为(0,3).
∵抛物线的对称轴为直线x=-2,
∴点A与点B关于直线x=-2对称.
∴点B的坐标是(-1,0).
(2)设二次函数的关系式为y=ax2+bx+c,
∵二次函数的图象经过点C(0,3)和点A(-3,0),
且对称轴是直线x=-2,
∴可列得方程组
解得:
∴二次函数的关系式为y=x2+4x+3.
(或将点A,点B,点C的坐标依次代入关系式中求出a,b,c的值
也可)
(3)由图象观察可知,当-3<x<0时,二次函数值小于一次函数
值.
8.如图,已知函数L1:
y=x2-4x+3与x轴交于A,B两点(点A在点B
左边),与y轴交于点C.
(1)写出二次函数L1的开口方向、对称轴和
顶点坐标;
(2)研究二次函数L2:y=kx2-4kx+3k(k≠0).
①写出二次函数L2与二次函数L1有关图象的两条相同的性质;
②若直线y=8k与抛物线L2交于E,F两点,问线段EF的长度是否
发生变化?如果不会,请求出EF的长度;如果会,请说明理由.
【解析】(1)抛物线y=x2-4x+3中,a=1,b=-4,c=3;
∴二次函数L1的开口向上,对称轴是直线x=2,顶点坐标(2,-1).
(2)①二次函数L2与L1有关图象的两条相同的性质:
对称轴为直线x=2或顶点的横坐标为2,
都经过A(1,0),B(3,0)两点;
②线段EF的长度不会发生变化.
∵直线y=8k与抛物线L2交于E,F两点,
∴kx2-4kx+3k=8k,
∵k≠0,∴x2-4x+3=8,
解得:x1=-1,x2=5,∴EF=x2-x1=6,
∴线段EF的长度不会发生变化.
9.某汽车租赁公司拥有20辆汽车.据统计,
当每辆车的日租金为400元时,可全部租出;当每
辆车的日租
金每增加50元,未租出的车将增加1辆;公司平均每日的各项支
出共4
800元.设公司每日租出x辆车时,日收益为y元.(日收
益=日租金收入-平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为元_______(用含x
的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少
元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
【解析】(1)∵某汽车租赁公司拥有20辆汽车.据统计,当每辆
车的日租金为400元时,可全部租出;当每辆车的日租金每增加
50元,未租出的车将增加1辆;
∴当全部未租出时,每辆租金为:400+20×50=1
400元,
∴公司每日租出x辆车时,每辆车的日租金为:1400-50x.
故答案为:1
400-50x.
(2)根据题意得出:
y=x(-50x+1400)-4
800
=-50x2+1
400x-4
800=-50(x-14)2+5
000.
当x=14时,y有最大值5
000.
∴当每日租出14辆车时,租赁公司日收益最大,最大值为
5
000元.
(3)要使租赁公司日收益不盈也不亏,即y=0.
即-50(x-14)2+5
000=0,
解得x1=24,x2=4,
∵x=24不合题意,舍去.∴当每日租出4辆时,租赁公司日收益
不盈也不亏.
第26章
单元复习课
一、二次函数的概念
1.定义
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
2.由二次函数的定义可知二次函数必须满足三个条件:
(1)函数关系式是整式;
(2)化简后自变量的最高次数必须是2;
(3)二次项的系数不为0,一次项系数b和常数项c可以为任意实
数.
3.二次函数定义的应用
与二次函数定义有关的问题的应用有两个方面,解题的关键是
理解二次函数的概念:
一是根据定义判断函数的类型,在判断时要先把函数化成一般
形式,再严格按照定义,对含有字母系数的二次函数,着重看
二次项的系数是否为零;
二是根据二次函数的定义,求某些字母的取值范围,解题的关
键是根据次数构建关于所求字母的方程,然后求解.
注:(1)利用二次函数的定义解题时,尤其是含有字母系数的
函数,应特别留意二次项的系数是否为0.
(2)根据实际问题列函数关系式时,要注意自变量的取值范围
需保证使实际问题有意义.
二、二次函数的图象及其性质
1.二次函数y=ax2的图象及其性质
(1)抛物线y=ax2的顶点是坐标原点,对称轴是y轴.
(2)①当a>0时,图象位于x轴的上方,抛物线开口向上,顶点为
其最低点;在对称轴的左侧,y随x的增大而减小,在对称轴的
右侧,y随x的增大而增大;
②当a<0时,图象位于x轴的下方,抛物线开口向下,顶点为其最
高点;在对称轴的左侧,y随x的增大而增大,在对称轴的右
侧,y随x的增大而减小;
(3)①当a>0时,函数y=ax2有最小值,最小值是0;
②当a<0时,函数y=ax2有最大值,最大值是0.
注:应用函数图象及其性质时,要注意数与形的有机结合,特
别是利用函数的图象解决问题时,需充分考虑抛物线的对称性.
2.二次函数y=ax2+bx+c的图象及其性质
(1)几种特殊的二次函数图象的特征
函数关系式
开口方向
对称轴
顶点坐标
y=ax2+k
当a>0时,开口向上;当a<0时,开口向下
x=0
(0,k)
y=a(x-h)2
x=h
(h,0)
y=a(x-h)2+k
x=h
(h,k)
(2)二次函数y=ax2+bx+c的图象及其性质
函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
图象
a>0
a<0
函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
性质
①抛物线开口向上
①抛物线开口向下
②对称轴是直线
顶点是
③当x<
时,y随x的
增大而减小;当x>
时,y随x的增大而增大
③当x<
时,y随x的
增大而增大;当x>
时,y随x的增大而减小
④抛物线有最低点,当
x=
时,y有最小值,
y最小值=
④抛物线有最高点,当
x=
时,y有最大值,
y最大值=
3.系数a,b,c与二次函数的图象
(1)a决定开口方向及开口大小
当a>0时,开口向上,当a<0时,开口向下;|a|越大,抛物
线的开口越小;
(2)b和a共同决定抛物线对称轴的位置
由于抛物线y=ax2+bx+c(a≠0)的对称轴是直线
故:
①b=0时,对称轴为y轴;
②
>0(即a,b同号)时,对称轴在y轴左侧;
③
<0(即a,b异号)时,对称轴在y轴右侧.
(3)c的大小决定抛物线y=ax2+bx+c与y轴交点的位置
当x=0时,y=c,∴抛物线y=ax2+bx+c与y轴有且只有一个交点
(0,c).即①c=0,抛物线经过原点;②c>0,与y轴交于正半轴;
③c<0,与y轴交于负半轴.
以上三点中,当结论和条件互换时,仍成立.
4.二次函数图象的平移规律
平移不改变图形的形状和大小,因此抛物线在平移的过程中,
图象的形状、开口方向必相同,即a不变,所以抛物线
y=ax2+bx+c可以由y=ax2平移得到.其平移的规律用语言来表示
可以归结为:“上加下减,左加右减”,平移时具体的对应关
系可以用下列框图来表示:
三、二次函数的相关计算
1.求抛物线的顶点、对称轴的方法:
(1)公式法:
∴顶点是
,对称轴是直线
(2)配方法:运用配方的方法,将抛物线的关系式化为
y=a(x-h)2+k的形式,得到顶点为(h,k),对称轴是直线x=h.将
关系式y=ax2+bx+c化为y=a(x-h)2+k的形式,其基本步骤是:
①提取二次项的系数,把二次项的系数化为1(注意与一元二次
方程中配方法的区别);
②对上面的二次函数的二次三项式配方,即加上一次项系数一
半的平方,配方时不能改变原式的值;
③写成y=a(x-h)2+k的形式.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称
图形,所以对称的两点的连线的垂直平分线是抛物线的对称
轴,对称轴与抛物线的交点是顶点.
若已知抛物线上两点
(x1,y)、(x2,y),则对称轴方程可以表示为:
2.求二次函数关系式
(1)二次函数关系式常用的有三种形式
①一般式:y=ax2+bx+c(a≠0);
②顶点式:y=a(x-h)2+k(a≠0)
;
③交点式:y=a(x-x1)(x-x2)(a≠0).
(2)恰当地选择二次函数的表达形式求关系式
求解二次函数关系式一般用待定系数法,根据所给条件的不
同,要灵活选用函数关系式的表达形式:
①当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+
c(a≠0)的形式,然后组成三元一次方程组来求解.
②当已知抛物线的顶点或对称轴或最大(小)值时,通常设为顶
点式y=a(x-h)2+k(a≠0)的形式.
③当已知抛物线与x轴的交点(或交点横坐标)或已知抛物线与x
轴一个交点和对称轴时,通常设为交点式:y=a(x-x1)(x-
x2)(a≠0).
注:(1)用待定系数法求解二次函数的关系式,题目给出的方式
比较灵活,除上述三种方式外,往往还结合函数的性质提供一
些条件.如
①抛物线的形状相同(形状相同的两个抛物线的二次项的系数相
同或互为相反数,在解题时要注意,防止漏解);
②与坐标轴的交点坐标所围成的三角形的面积;
③依据函数增减性,通过增减性的不同确定抛物线的对称轴,
再设为顶点式求解;
④结合函数的图象平移给出某些点的坐标;
⑤应用函数图象与x轴的交点与一元二次方程的关系,借助方程
的解给出条件.
(2)不论应用何种形式设关系式,最后求得的结果一般化为一般
形式.
(3)当题目条件中点的条件不足三个时,要充分利用二次函数的
对称性转化条件.
四、二次函数与一元二次方程的关系
1.二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)
的关系
(1)“数”的角度:当二次函数y=ax2+bx+c(a≠0)的函数值等于
0时,相应的自变量的值即为一元二次方程ax2+bx+c=0(a≠0)的
解.
(2)“形”的角度:若抛物线y=ax2+bx+c(a≠0)与x轴两交点为
A(x1,0),B(x2,0),则一元二次方程ax2+bx+c=0(a≠0)的两个根
为x1,x2.
2.抛物线与x轴的交点情况与一元二次方程的根的判别式的关
系:
(1)有两个交点 b2-4ac>0;
(2)有一个交点(顶点在x轴上) b2-4ac=0;
(3)没有交点 b2-4ac<0.
注:根据抛物线的开口方向和顶点的位置也可以判断抛物线与x
轴的交点个数,如a>0,顶点在x轴的上方,则抛物线与x轴没
有交点.
3.应用二次函数图象求方程的近似根的步骤
(1)根据方程确定与方程有关的二次函数;
(2)画出二次函数的图象;
(3)初步估值,确定一元二次方程的根的取值范围,即确定抛物
线与x轴交点的横坐标的大体范围;
(4)在初步估值确定的范围内,从小到大或从大到小依次取值,
借助计算器探索,确定近似值.
4.直线与抛物线的交点
(1)y轴与抛物线y=ax2+bx+c的交点为(0,c).
(2)与y轴平行的直线x=h与抛物线y=ax2+bx+c有且只有一个交点
(h,ah2+bh+c).
(3)抛物线与x轴的交点
二次函数y=ax2+bx+c的图象与x轴的两个交点的横坐标x1,x2,
是对应的一元二次方程ax2+bx+c=0的两个实数根.抛物线与x轴
的交点情况可以由对应的一元二次方程的根的判别式判定.
(4)平行于x轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点
时,两交点的纵坐标相等,设纵坐标为k,则横坐标是
ax2+bx+c=k的两个实数根.
(5)一次函数y=kx+n(k≠0)的图象l与二次函数y=ax2+bx+c(a≠0)
的图象G的交点,由方程组
的解的数目来确定:
①方程组有两组不同的解 l与G有两个交点;②方程组只有一
组解 l与G只有一个交点;③方程组无解 l与G没有交点.
(6)抛物线与x轴两交点之间的距离:若抛物线y=ax2+bx+c与x轴
两交点为A(x1,0),B(x2,0),由于x1,x2是方程ax2+bx+c=0的两
个根,故x1+x2=
x1·x2=
五、应用二次函数解决实际问题
二次函数是反映现实世界中变量间的数量关系和变化规律的一
种常见的数学模型,它的应用体现的核心问题是数学建模思想
的应用,解题的关键是准确理解题意,建立合适的函数模型.解
决此类问题的基本思路是:(1)理解问题;(2)分析问题中的变
量和常量以及它们之间的关系;(3)用函数关系式表示它们之间
的关系;(4)计算或求解,并应用函数的性质作出判断;(5)检
验结果的合理性.
注:1.不能选择恰当的函数关系式表示实际问题中的数量关系;
2.利用二次函数解决实际问题时,对题意理解不清,导致无法列出正确的函数关系式;
3.不考虑自变量的取值范围,所求最值与实际不符;
4.易把求最大值和最小值的公式与一元二次方程的求根公式相混.
实际问题
实际问题
的解决
二次函数
y=ax2+bx+c(a
0)
二次函数与一元
二次方程的关系
二次函数的
图象与性质
关系式
图
象
性
质
平移规律
二次函数的对称轴及顶点坐标
【相关链接】
确定二次函数对称轴及顶点坐标的两种方法
1.公式法:对称轴是直线
顶点坐标是
2.配方法:将二次函数通过配方化为y=a(x-h)2+k(a≠0)的形
式,对称轴为x=h,顶点坐标是(h,k).
【例1】已知二次函数y=2(x-3)2+1.下列说
法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其
图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小,则其
中说法正确的有(
)
(A)1个
(B)2个
(C)3个
(D)4个
【思路点拨】根据抛物线y=a(x-h)2+k(a≠0)的性质进行判断.
【自主解答】选A.∵2>0,∴图象的开口向上,故①错误;
图象的对称轴为直线x=3,故②错误;
其图象顶点坐标为(3,1),故③错误;
当x<3时,y随x的增大而减小,④正确.
综上所述,说法正确的有④,共1个.
确定函数关系式
【相关链接】
待定系数法主要用于确定二次函数的关系式
1.当已知抛物线上任意三点坐标时,可以通过设函数关系式为
一般式y=ax2+bx+c(a≠0)进行求解;
2.当已知抛物线顶点坐标、对称轴或最值时,可以通过设函数
关系式为y=a(x-h)2+k(a≠0)进行求解;
3.如果已知抛物线与x轴的两个交点(x1,0)(x2,0)时,可设为
交点式y=a(x-x1)(x-x2)进行求解.
【例2】如图,抛物线y=x2+bx+c经过坐标
原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且
S△OAB=3,求点B的坐标.
【思路点拨】(1)
(2)
(3)
【自主解答】(1)把(0,0),(2,0)代入y=x2+bx+c得
解得
所以解析式为y=x2-2x.
(2)∵y=x2-2x=(x-1)2-1,
∴顶点为(1,-1).
对称轴为直线x=1.
(3)设点B的坐标为(m,n),则
解得n=3或n=-3,
∵顶点纵坐标为-1,-3<-1(或x2-2x=-3中,x无解)
∴n=3,
∴x2-2x=3.
解得x1=3,x2=-1.
所以点B的坐标为(3,3)或(-1,3).
二次函数的图象与性质
【相关链接】
某些特殊形式的代数式的符号的判断:
(1)
a+b+c,即x=1时y的值.
(2)
b2-4ac,根据图象与x轴交点的个数判断.
系数的符号
图象特征
a的符号
开口向上 a>0,开口向下 a<0
b的符号
左同右异,顶点在y轴左侧,b与a符号相同;顶点在y轴右侧,b与a符号相异.
c的符号
c为图象与y轴交点的纵坐标
【例3】已知二次函数y=ax2+bx+c(a≠0)的图
象如图所示,现有下列结论:①
b2-4ac>0;②
a>0;③
b>
0;④
c>0;⑤9a+3b+c<0,则其中结论正确的个数是(
)
(A)2个
(B)3个
(C)4个
(D)5个
【思路点拨】根据函数图象中抛物线的开口方向判断a的符号,
再结合对称轴的位置判断b的符号;根据抛物线与y轴交点的位
置判断c的符号;根据抛物线与x轴交点的个数判断b2-4ac的符
号;根据对称轴x=1,可判断(3,0)的对称点为(-1,0),由x=-1时
的y值的符号来判断9a+3b+c的符号.
【自主解答】选B.①根据图象知,二次函数与x轴有两个交点,
所以b2-4ac>0,∴①正确;
②根据图象知,该函数图象的开口向上,∴a>0,②正确;③又
对称轴
∴b<0,∴③错误;
④该函数图象交于y轴的负半轴,∴c<0,∴④错误;
⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称
点是(3,0);当x=-1时,y<0,所以当x=3时,也有y<0,
即9a+3b+c<0,⑤正确.所以①②⑤正确.
二次函数的应用
【相关链接】
在应用二次函数解决实际问题时,首先要注意对实际问题进行
观察分析,并从中抽象出相应的数量关系,建立二次函数模
型,进而利用二次函数的图象与性质解答.在解答时要注意实际
问题中数量及数量关系的意义要符合实际问题的要求和限制,特
别是自变量取值范围的限制及其对应的函数值的取值范围的要
求.
【例4】许多家庭
以燃气作为烧水做饭的燃料,节约用
气是我们日常生活中非常现实的问
题,某款燃气灶旋钮位置从0度到90度
(如图),燃气关闭时,燃气灶旋钮的位
置为0度,旋钮角度越大,燃气流量越大,燃气开到最大时,旋钮角
度为90度.为测试燃气灶旋钮在不同位置上的燃气用量,在相同条
件下,选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋
旋钮角度(度)
20
50
70
80
90
所用燃气量(升)
73
67
83
97
115
钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度
的范围是18≤x≤90),记录相关数据得到下表:
(1)请你从所学习过的一次函数、反比例函数和二次函数中确定
哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律 说明
确定是这种函数而不是其他函数的理由,并求出它的关系式.
(2)当旋钮角度为多少时,烧开一壶水所用燃气量最少 最少是多
少
(3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最
节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭
以前每月的平均燃气用量.
【思路点拨】(1)根据列表中的相关数据,分别选取合适的点的
坐标求出一次函数、反比例函数和二次函数的关系式,再用另
外的点加以验证,得出结论.
(2)根据二次函数的性质,解决问题.
(3)根据题意,结合(1),(2)分析求出结果.
【自主解答】(1)若设y=kx+b(k≠0),由
解得
所以
把x=70代入得y=63≠83,所以不符合.
若设
由
解得k=1
460,
所以
把x=50代入得y=29.2≠67,所以不符合;
若设y=ax2+bx+c,则由
解得
所以
把x=80代入得y=97,把x=90代入得y=115,符合题意.
所以选用二次函数能表示所用燃气量y升与旋钮角度x度的变化
规律.
(2)由(1)得
所以当x=40时,y取得最小值65.
即当旋钮角度为40度时,烧开一壶水所用燃气量最少,最少为
65升.
(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开
到最大时烧开一壶水节约用燃气115-65=50(升),
设该家庭以前每月平均用燃气量为a立方米,则由题意得
解得a=23(立方米),
即该家庭以前每月平均用气量为23立方米.
【命题揭秘】
结合近几年中考试题分析,二次函数的内容考查主要有以下特
点:
1.命题方式为二次函数表达式的确定,二次函数的图象与性质
的应用,判定二次函数的顶点坐标、开口方向、对称轴方程,
用函数观点解决方程(组)、不等式问题;二次函数的实际应
用,题型多样,涉及选择题、填空题与解答题.
2.命题的热点为二次函数表达式的求法、二次函数的实际应
用,二次函数与一次函数、反比例函数的综合应用,以及函数
与方程(组)、不等式知识相融合的综合题目的考查.
1.下列二次函数中,图象以直线x=2为对称
轴、且经过点(0,1)的是(
)
(A)y=(x-2)2+1
(B)y=(x+2)2+1
(C)y=(x-2)2-3
(D)y=(x+2)2-3
【解析】选C.根据以直线x=2为对称轴可知选项A,C符合,再根据图象经过点(0,1)知选项C符合.
2.已知二次函数y=-x2+x-
,当自变量x取m时,
对应的函数值大于0,当自变量x分别取m-1,m+1时对应的函数值
为y1,y2,则必有y1,y2满足(
)
(A)y1>0,y2>0
(B)y1<0,y2<0
(C)y1<0,y2>0
(D)y1>0,y2<0
【解析】选B.∵
图象开口向下,与x
轴两交点都在0到1之间,由当自变量x取m时,对应的函数值大于0,
得0<m<1,∴-1<m-1<0,
1<m+1<2,根据图象可得y1<0,y2<0.
故选B.
3.竖直向上发射的小球
的高度h(m)关于运动时间t(s)的函数表达
式为h=at2+bt,其图象如图所示,若小球在
发射后第2秒与第6秒时的高度相等,则下列
时刻中小球的高度最高的是(
)
(A)第3秒
(B)第3.5秒
(C)第4.2秒
(D)第6.5秒
【解析】选C.由题意知,当t=4时小球的高度最高,当t=3与t=5时
小球高度相等,当t<4时,h随t的增大而增大;当t>4时,h随t的
增大而减小,∴四个选项中,当t=4.2时,小球高度最高.
4.如图是二次函数y=ax2+bx+c(a≠0)的图
象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c
=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是
__________
.(只要求填写正确命题的序号)
【解析】由图可知,当x=1时,y=0,即a+b+c=0;又对称轴为-1,
则
则b=2a;由抛物线的对称性可知,此二次函数与x轴
的另一个交点坐标为(-3,0),根据函数与方程的关系可知,方程
ax2+bx+c=0的两根分别为-3和1;由a+b+c=0得,a+c=-b,则
a-2b+c=-3b,因为a>0,则b=2a>0,所以a-2b+c=-3b<0,所以
①③正确.
答案:①③
5.如图,已知抛物线y=x2+bx+c经过点(0,
-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)
和(3,0)之间.你所确定的b的值是_________.
【解析】把点(0,-3)代入函数的关系式可得c=-3,只要是再把一
个点的坐标代入关系式就可求出b值.由“与x轴的一个交点在
(1,0)和(3,0)之间”可选择满足条件的点的坐标代入即可,如代
入(2,0)可求
答案:
(答案不唯一)
6.如图,已知函数
与y=ax2+bx(a>0,b>0)
的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+
=0
的解为__________.
【解析】∵P的纵坐标为1,
∴P的横坐标为-3.
∵
可化为关于x的方程ax2+bx=
的形式,
∴此方程的解即为两函数图象交点的横坐标的值,
∴x=-3.
答案:x=-3
7.已知:抛物线与直线
y=x+3分别交于x轴和y轴上同一点,交点分
别是点A和点C,且抛物线的对称轴为直线
x=-2.
(1)求出抛物线与x轴的两个交点A,B的
坐标;
(2)试确定抛物线的关系式;
(3)观察图象,请直接写出二次函数值小于一次函数值的自变量
x的取值范围.
【解析】(1)y=x+3中,
当y=0时,
x=-3,
∴点A的坐标为(-3,0).
当x=0时,y=3,
∴点C坐标为(0,3).
∵抛物线的对称轴为直线x=-2,
∴点A与点B关于直线x=-2对称.
∴点B的坐标是(-1,0).
(2)设二次函数的关系式为y=ax2+bx+c,
∵二次函数的图象经过点C(0,3)和点A(-3,0),
且对称轴是直线x=-2,
∴可列得方程组
解得:
∴二次函数的关系式为y=x2+4x+3.
(或将点A,点B,点C的坐标依次代入关系式中求出a,b,c的值
也可)
(3)由图象观察可知,当-3<x<0时,二次函数值小于一次函数
值.
8.如图,已知函数L1:
y=x2-4x+3与x轴交于A,B两点(点A在点B
左边),与y轴交于点C.
(1)写出二次函数L1的开口方向、对称轴和
顶点坐标;
(2)研究二次函数L2:y=kx2-4kx+3k(k≠0).
①写出二次函数L2与二次函数L1有关图象的两条相同的性质;
②若直线y=8k与抛物线L2交于E,F两点,问线段EF的长度是否
发生变化?如果不会,请求出EF的长度;如果会,请说明理由.
【解析】(1)抛物线y=x2-4x+3中,a=1,b=-4,c=3;
∴二次函数L1的开口向上,对称轴是直线x=2,顶点坐标(2,-1).
(2)①二次函数L2与L1有关图象的两条相同的性质:
对称轴为直线x=2或顶点的横坐标为2,
都经过A(1,0),B(3,0)两点;
②线段EF的长度不会发生变化.
∵直线y=8k与抛物线L2交于E,F两点,
∴kx2-4kx+3k=8k,
∵k≠0,∴x2-4x+3=8,
解得:x1=-1,x2=5,∴EF=x2-x1=6,
∴线段EF的长度不会发生变化.
9.某汽车租赁公司拥有20辆汽车.据统计,
当每辆车的日租金为400元时,可全部租出;当每
辆车的日租
金每增加50元,未租出的车将增加1辆;公司平均每日的各项支
出共4
800元.设公司每日租出x辆车时,日收益为y元.(日收
益=日租金收入-平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为元_______(用含x
的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少
元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
【解析】(1)∵某汽车租赁公司拥有20辆汽车.据统计,当每辆
车的日租金为400元时,可全部租出;当每辆车的日租金每增加
50元,未租出的车将增加1辆;
∴当全部未租出时,每辆租金为:400+20×50=1
400元,
∴公司每日租出x辆车时,每辆车的日租金为:1400-50x.
故答案为:1
400-50x.
(2)根据题意得出:
y=x(-50x+1400)-4
800
=-50x2+1
400x-4
800=-50(x-14)2+5
000.
当x=14时,y有最大值5
000.
∴当每日租出14辆车时,租赁公司日收益最大,最大值为
5
000元.
(3)要使租赁公司日收益不盈也不亏,即y=0.
即-50(x-14)2+5
000=0,
解得x1=24,x2=4,
∵x=24不合题意,舍去.∴当每日租出4辆时,租赁公司日收益
不盈也不亏.
