2020春华师版九下数学 27.1.1圆的基本元素 课件(29张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.1.1圆的基本元素 课件(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 784.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览








文档简介
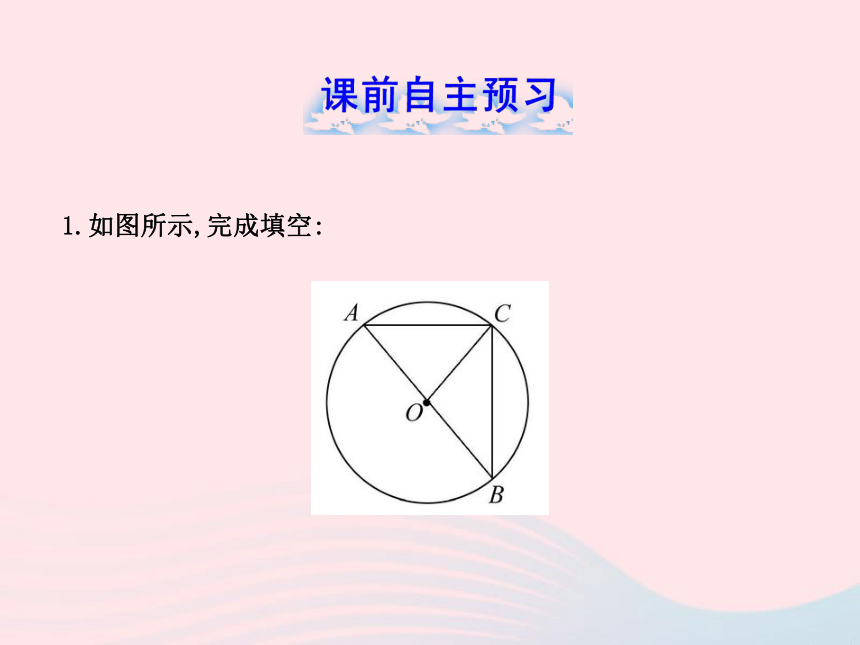
课件29张PPT。1.圆的基本元素 1.如图所示,完成填空: (1)图中以点O为圆心的圆叫做“____”,记为“____”.
(2)半径:线段___,___,___都是⊙O的半径.
(3)直径:线段___是⊙O的直径.
(4)弦:线段___,___,___都是⊙O中的弦.圆O⊙OOAOBOCABACBCAB(5)弧:_____BC,AC,BAC都是⊙O中的弧,
记作___,___,_____.
劣弧:_____半圆周的圆弧. ___,___都是⊙O中的劣弧.
优弧:_____半圆周的圆弧. ____,____都是⊙O中的优弧.
(6)圆心角:______,______都是⊙O中的圆心角,____是这些角的顶点. 曲线小于大于∠AOC∠BOC点O2.圆的基本概念辨析
(1)圆的位置由_____确定,圆的大小由_____长度确定,_____
相等的两个圆为等圆.
(2)直径一定___弦(最长的弦),但是弦不一定___直径.
【点拨】一定要用三个字母表示优弧.圆心半径半径是是【预习思考】优弧与劣弧有哪些不同点?
提示:优弧与劣弧的不同是它们与它们所在的圆的半圆周的大小不同,劣弧小于半圆周,优弧大于半圆周,半圆既不是劣弧也不是优弧. 圆的有关概念的理解
【例1】在以下所给的命题中:①直径是弦;②弦是直径;
③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是
等弧;⑤长度相等的弧是等弧.
其中正确的个数为( )
(A)1 (B)2 (C)3 (D)4【解题探究】选C.1.因为直径是弦,但弦不一定是直径,所以可
判断①正确,②错误.
2.因为半圆是弧,但弧不一定是半圆,所以可判断③正确.
3.因为等弧必须是在同圆或等圆中能够互相重合的弧,长度相等
的弧不一定是等弧,所以可判断④正确,⑤错误.
4.由以上分析可知①③④正确,因而选C.【互动探究】解决此类问题的关键是什么?
提示:正确理解圆的基本元素的概念是解决问题的关键.【规律总结】
判断两段弧是等弧的两个条件
1.在同圆或等圆中;
2.能够互相重合,两者缺一不可.【跟踪训练】
1.在同圆或等圆中,下列结论正确的是( )
(A)弦相等 (B)劣弧都相等
(C)过圆心的弦相等 (D)优弧相等
【解析】选C.因为在同圆或等圆中,有无数条弦,无数条优弧,无
数条劣弧,所以它们不一定都相等,而过圆心的弦是直径,一定相
等,因此C正确. 2.以已知点O为圆心,已知线段a为半径作圆,可以作( )
(A)1个 (B)2个 (C)3个 (D)无数个
【解析】选A.圆心O确定圆的位置,线段a确定圆的大小,所以只
能作一个圆.3.已知⊙O的半径长为8 cm,则⊙O上两点间的距离最长为
_____ cm.
【解析】因为⊙O上两点间的距离最长为直径的长,所以最长
距离为16 cm.
答案:16 与圆相关的定义的运用
【例2】(5分)如图,在⊙O中,OA=OB,OC,OD交AB于E,F,AE=BF,求
证:OE=OF.
易错提醒:分不清半径和圆中线段. 【规范解答】∵OA=OB,
∴∠A=∠B.………………………………………………1分
又∵AE=BF,………………………………………………2分
∴△OAE≌△OBF.…………………………………………4分
∴OE=OF.…………………………………………………5分【互动探究】在运用圆的有关概念进行证明和计算时,要注意什
么?
提示:(1)结合图形,理清各个相关概念的意义;
(2)注意构建基本图形.【规律总结】
与圆的概念有关的证明和计算题两种类型
类型一:利用同圆或等圆的半径相等,借助全等三角形的知识证
明线段相等或平行;
类型二:在同圆中利用半径相等,结合等腰三角形进行证明或计
算.【跟踪训练】
4.如图,直线l1∥l2,点A在直线l1上,以点
A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点,
连结AC,BC.若∠ABC=54°,则∠1的大小为( )
(A)36° (B)54° (C)72° (D)73°【解析】选C.如图,
∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°.
∵以点A为圆心,适当长为半径画
弧,分别交直线l1,l2于B,C两点,
∴AC=AB,∴∠ACB=∠ABC=54°.
∵∠1+∠ACB+∠2=180°,∴∠1=72°.【变式训练】如图,在Rt△ABC中,∠C=90°,
AC=3,将其绕B点顺时针旋转一周,则分别以
BA,BC为半径的圆形成一圆环,该圆环的面
积为( )
(A) π (B)3π (C)9π (D)6π
【解析】选C.圆环的面积为πAB2-πBC2
=π(AB2-BC2)=πAC2=32π=9π.5.如图,AB为⊙O的直径,
点C在⊙O上,若∠C=16°,则∠BOC的度数
是( )
(A)74° (B)48°
(C)32° (D)16°
【解析】选C.由AO=OC,得∠A=∠C=16°,
∠BOC=2∠A=32°.6.在⊙O中,点B在⊙O上,
四边形AOCB是矩形,对角线AC的长为5,则
⊙O的半径长为________.
【解析】连结OB.由四边形AOCB是矩形,得
AC=OB(矩形的对角线相等),又因为AC=5,
所以OB=5,所以⊙O的半径长为5.
答案:57.如图,C是⊙O直径AB上一点,过C作弦DE,
使DC=EC,∠AOD=40°,求∠BOE 的度数.
【解析】∵OC=OC,OD=OE,DC=EC,
∴△ODC≌△OEC,
∴∠AOD=∠AOE=40°,
∴∠BOE=180°-∠AOE=180°-40°=140°.1.如图,⊙O中,点A,O,D,点E,D,C以及点
B,O,C分别在一条直线上,图中弦的条数
有( )
(A)2条 (B)3条
(C)4条 (D)5条
【解析】选B.圆上共4个点,而连结它们的只有三条线段,所以图
中弦共有3条.2.以点A(3,0)为圆心,以5为半径画圆,则圆A与x轴交点坐标为
( )
(A)(0,-2),(0,8) (B)(-2,0),(8,0)
(C)(0,-8),(0,2) (D)(-8,0),(2,0)
【解析】选B.因为圆心在x轴上,与x轴相交于两点,
∴两点的纵坐标都为0,∵圆的半径是5,
∴两点的横坐标为3-5=-2,3+5=8.
即两点的坐标为(-2,0),(8,0).3.以点P(0,-1)为圆心,3为半径画圆,分别
交y轴的正半轴、负半轴于点A,B,则A点坐
标为________,B点坐标为________.
【解析】因为点P(0,-1)在y轴上,
根据题意,即在y轴上找两点,使AP=BP=3,
观察数轴得A(0,2),B(0,-4).
答案:(0,2) (0,-4)4.已知:如图,OA,OB为⊙O的半径,C,D分别
为OA,OB的中点,若AD=3厘米,则BC=_____厘米.
【解析】∵OA,OB为⊙O的半径,
∴OB=OA.
∵C,D分别为OA,OB的中点,∴OC=OD.
∵∠AOD是公共角,
∴△BOC≌△AOD.∴BC=AD=3厘米.
答案:35.如图所示,AB是⊙O的直径,点C在⊙O上,且OD∥BC.
求证:直线OD是AC的垂直平分线.
【证明】如图所示,连结OC.
∵OD∥BC,O为AB的中点,
∴D是AC的中点,
∵OA=OC,
∴OD是等腰△AOC底边上的高线,
∴直线OD是AC的垂直平分线.
(2)半径:线段___,___,___都是⊙O的半径.
(3)直径:线段___是⊙O的直径.
(4)弦:线段___,___,___都是⊙O中的弦.圆O⊙OOAOBOCABACBCAB(5)弧:_____BC,AC,BAC都是⊙O中的弧,
记作___,___,_____.
劣弧:_____半圆周的圆弧. ___,___都是⊙O中的劣弧.
优弧:_____半圆周的圆弧. ____,____都是⊙O中的优弧.
(6)圆心角:______,______都是⊙O中的圆心角,____是这些角的顶点. 曲线小于大于∠AOC∠BOC点O2.圆的基本概念辨析
(1)圆的位置由_____确定,圆的大小由_____长度确定,_____
相等的两个圆为等圆.
(2)直径一定___弦(最长的弦),但是弦不一定___直径.
【点拨】一定要用三个字母表示优弧.圆心半径半径是是【预习思考】优弧与劣弧有哪些不同点?
提示:优弧与劣弧的不同是它们与它们所在的圆的半圆周的大小不同,劣弧小于半圆周,优弧大于半圆周,半圆既不是劣弧也不是优弧. 圆的有关概念的理解
【例1】在以下所给的命题中:①直径是弦;②弦是直径;
③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是
等弧;⑤长度相等的弧是等弧.
其中正确的个数为( )
(A)1 (B)2 (C)3 (D)4【解题探究】选C.1.因为直径是弦,但弦不一定是直径,所以可
判断①正确,②错误.
2.因为半圆是弧,但弧不一定是半圆,所以可判断③正确.
3.因为等弧必须是在同圆或等圆中能够互相重合的弧,长度相等
的弧不一定是等弧,所以可判断④正确,⑤错误.
4.由以上分析可知①③④正确,因而选C.【互动探究】解决此类问题的关键是什么?
提示:正确理解圆的基本元素的概念是解决问题的关键.【规律总结】
判断两段弧是等弧的两个条件
1.在同圆或等圆中;
2.能够互相重合,两者缺一不可.【跟踪训练】
1.在同圆或等圆中,下列结论正确的是( )
(A)弦相等 (B)劣弧都相等
(C)过圆心的弦相等 (D)优弧相等
【解析】选C.因为在同圆或等圆中,有无数条弦,无数条优弧,无
数条劣弧,所以它们不一定都相等,而过圆心的弦是直径,一定相
等,因此C正确. 2.以已知点O为圆心,已知线段a为半径作圆,可以作( )
(A)1个 (B)2个 (C)3个 (D)无数个
【解析】选A.圆心O确定圆的位置,线段a确定圆的大小,所以只
能作一个圆.3.已知⊙O的半径长为8 cm,则⊙O上两点间的距离最长为
_____ cm.
【解析】因为⊙O上两点间的距离最长为直径的长,所以最长
距离为16 cm.
答案:16 与圆相关的定义的运用
【例2】(5分)如图,在⊙O中,OA=OB,OC,OD交AB于E,F,AE=BF,求
证:OE=OF.
易错提醒:分不清半径和圆中线段. 【规范解答】∵OA=OB,
∴∠A=∠B.………………………………………………1分
又∵AE=BF,………………………………………………2分
∴△OAE≌△OBF.…………………………………………4分
∴OE=OF.…………………………………………………5分【互动探究】在运用圆的有关概念进行证明和计算时,要注意什
么?
提示:(1)结合图形,理清各个相关概念的意义;
(2)注意构建基本图形.【规律总结】
与圆的概念有关的证明和计算题两种类型
类型一:利用同圆或等圆的半径相等,借助全等三角形的知识证
明线段相等或平行;
类型二:在同圆中利用半径相等,结合等腰三角形进行证明或计
算.【跟踪训练】
4.如图,直线l1∥l2,点A在直线l1上,以点
A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点,
连结AC,BC.若∠ABC=54°,则∠1的大小为( )
(A)36° (B)54° (C)72° (D)73°【解析】选C.如图,
∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°.
∵以点A为圆心,适当长为半径画
弧,分别交直线l1,l2于B,C两点,
∴AC=AB,∴∠ACB=∠ABC=54°.
∵∠1+∠ACB+∠2=180°,∴∠1=72°.【变式训练】如图,在Rt△ABC中,∠C=90°,
AC=3,将其绕B点顺时针旋转一周,则分别以
BA,BC为半径的圆形成一圆环,该圆环的面
积为( )
(A) π (B)3π (C)9π (D)6π
【解析】选C.圆环的面积为πAB2-πBC2
=π(AB2-BC2)=πAC2=32π=9π.5.如图,AB为⊙O的直径,
点C在⊙O上,若∠C=16°,则∠BOC的度数
是( )
(A)74° (B)48°
(C)32° (D)16°
【解析】选C.由AO=OC,得∠A=∠C=16°,
∠BOC=2∠A=32°.6.在⊙O中,点B在⊙O上,
四边形AOCB是矩形,对角线AC的长为5,则
⊙O的半径长为________.
【解析】连结OB.由四边形AOCB是矩形,得
AC=OB(矩形的对角线相等),又因为AC=5,
所以OB=5,所以⊙O的半径长为5.
答案:57.如图,C是⊙O直径AB上一点,过C作弦DE,
使DC=EC,∠AOD=40°,求∠BOE 的度数.
【解析】∵OC=OC,OD=OE,DC=EC,
∴△ODC≌△OEC,
∴∠AOD=∠AOE=40°,
∴∠BOE=180°-∠AOE=180°-40°=140°.1.如图,⊙O中,点A,O,D,点E,D,C以及点
B,O,C分别在一条直线上,图中弦的条数
有( )
(A)2条 (B)3条
(C)4条 (D)5条
【解析】选B.圆上共4个点,而连结它们的只有三条线段,所以图
中弦共有3条.2.以点A(3,0)为圆心,以5为半径画圆,则圆A与x轴交点坐标为
( )
(A)(0,-2),(0,8) (B)(-2,0),(8,0)
(C)(0,-8),(0,2) (D)(-8,0),(2,0)
【解析】选B.因为圆心在x轴上,与x轴相交于两点,
∴两点的纵坐标都为0,∵圆的半径是5,
∴两点的横坐标为3-5=-2,3+5=8.
即两点的坐标为(-2,0),(8,0).3.以点P(0,-1)为圆心,3为半径画圆,分别
交y轴的正半轴、负半轴于点A,B,则A点坐
标为________,B点坐标为________.
【解析】因为点P(0,-1)在y轴上,
根据题意,即在y轴上找两点,使AP=BP=3,
观察数轴得A(0,2),B(0,-4).
答案:(0,2) (0,-4)4.已知:如图,OA,OB为⊙O的半径,C,D分别
为OA,OB的中点,若AD=3厘米,则BC=_____厘米.
【解析】∵OA,OB为⊙O的半径,
∴OB=OA.
∵C,D分别为OA,OB的中点,∴OC=OD.
∵∠AOD是公共角,
∴△BOC≌△AOD.∴BC=AD=3厘米.
答案:35.如图所示,AB是⊙O的直径,点C在⊙O上,且OD∥BC.
求证:直线OD是AC的垂直平分线.
【证明】如图所示,连结OC.
∵OD∥BC,O为AB的中点,
∴D是AC的中点,
∵OA=OC,
∴OD是等腰△AOC底边上的高线,
∴直线OD是AC的垂直平分线.
