2020春华师版九下数学 27.2.1点与圆的位置关系课件(30张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.2.1点与圆的位置关系课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 767.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:08:31 | ||
图片预览











文档简介
课件30张PPT。1.点与圆的位置关系 1.点与圆共有几种位置关系?分别是什么?
答:三种,点在_____,点在_____,点在_____.
2.过平面内一个点可以作多少个圆?圆心在哪里?
答:_____个.圆心分布在整个平面.圆内圆上圆外无数3.过平面内两点可以作多少个圆?圆心O在什么位置?
答:__________________________________________________
_____.
4.过平面内不在同一直线上的A,B,C 三点可以作多少个圆?圆
心在哪里?
答:过不在同一直线上的A,B,C三点能作_____圆,圆心是AB和BC
的___________的交点.
【点拨】不在同一条直线上的三个点确定一个圆.过两点可以画无数个圆,圆心在两点所连线段的垂直平分线上一个垂直平分线5.经过三角形三个顶点的圆叫做三角形的_______.三角形_______
的圆心叫做这个三角形的外心.这个三角形叫做这个圆的_______
_____.三角形的外心就是三角形三条边的___________的交点,它
到三角形_________的距离相等.
【点拨】三角形的外心与三角形的形状有关,锐角三角形的外心
在三角形的内部,直角三角形的外心是斜边的中点,钝角三角形
的外心在三角形的外部. 外接圆外接圆内接三角形垂直平分线三个顶点【预习思考】经过平面内A,B,C三点能否画圆?
提示:不一定.当A,B,C三点在一条直线上时,不能画圆;当
A,B,C三点不在一条直线上时,可以画一个圆. 点与圆的位置关系
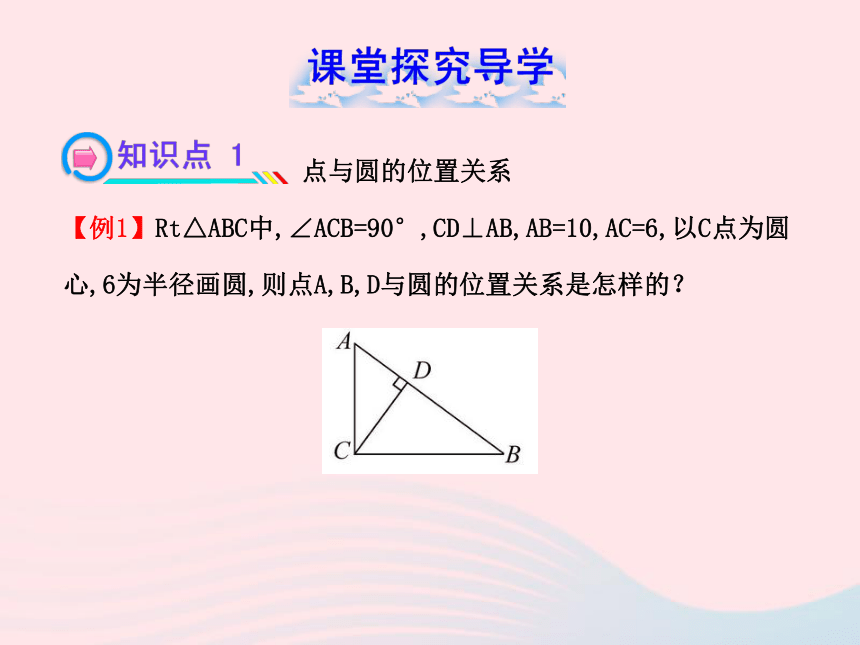
【例1】Rt△ABC中,∠ACB=90°,CD⊥AB,AB=10,AC=6,以C点为圆
心,6为半径画圆,则点A,B,D与圆的位置关系是怎样的?【解题探究】
(1)确定点与圆的位置关系除了半径,还要知道什么?
答:还要知道点到圆心的距离.
(2)点A,B,D到圆心C的距离分别是哪些线段的长?
答:分别是线段CA,CB,CD的长.
(3)试求线段CB和CD的长.
答:在Rt△ACB中,AC=6,AB=10,由勾股定理可得:
BC=8;∵
∴CD=4.8.(4)说出点A,B,D与圆的位置关系.
答:∵AC=6,⊙C的半径r为6, AC=r,
∴ 点A在圆上.
∵CD=4.8,⊙C的半径r为6, DC<r,
∴点D在圆内.
∵BC=8,⊙C的半径r为6, BC>r,
∴点B在圆外.【互动探究】如何确定点与圆的位置关系?
提示:比较点到圆心的距离d与圆的半径r的大小. 若d=r,则点
在圆上;若d>r,则点在圆外;若d<r,则点在圆内,反之亦然.【规律总结】
判断点与圆的位置关系“二步法”
1.确定圆的半径及点到圆心的距离;
2.比较大小,确定位置关系.【跟踪训练】
1.已知⊙O的直径为10 cm,P为⊙O外的一点,则OP的长不可
能是( )
(A)12 cm (B)8 cm
(C)6 cm (D)5 cm
【解析】选D.因为直径为10 cm,则⊙O的半径为5 cm.而点P
在⊙O外,即OP>5 cm,故选D.2.已知矩形ABCD的边AB=6,AD=8.如果以点A为圆心作⊙A,使
B,C,D三点中在圆内和在圆外都至少有一个点,那么⊙A的半径r
的取值范围是( )
(A)6<r<10 (B)8<r<10
(C)6<r≤8 (D)8<r≤10
【解析】选A.∵AB=6,AD=8,∴AC=10,
∴点C一定在圆外,点B一定在圆内,
∴⊙A的半径r的取值范围是6<r<10.3.已知点P到⊙O的最近距离为3 cm,最远距离为9 cm,求⊙O的
半径.
【解析】∵点P到⊙O的最近距离为3 cm,最远距离为9 cm,则当
点P在圆外时,⊙O的直径是9-3=6(cm),半径是3 cm;当点P在圆
内时,⊙O的直径是9+3=12(cm),半径为6 cm.
∴⊙O的半径为3 cm或6 cm. 确定圆的条件
【例2】(6分)如图所示,破残的圆形轮
片上,弦AB的垂直平分线交弧AB于点C,
交弦AB于点D.已知:AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆;(不写作法,
保留作图痕迹)
(2)求(1)中所作圆的半径.
特别提醒:圆心是弦的垂直平分线的交点. 【规范解答】
(1)连结AC,作弦AC的垂直平分线与弦AB的垂直平分线交于O点,
以O为圆心,OB长为半径作圆O,圆O就是此残片所在的圆,如图.
………………………………………3分(2)连结OB,设OB=x,BD=12 cm,OD=(x-8) cm,
则根据勾股定理列方程:x2=122+(x-8)2,……………………5分
解得:x=13.
答:圆的半径为13 cm.………………………………………6分【互动探究】1.作圆的关键是什么?
提示:作圆的关键是确定圆心的位置和半径的大小.
2.三角形有几个外接圆?
提示:任意一个三角形都有且只有一个外接圆.【规律总结】
作三角形外接圆时需注意的三个问题
1.圆心是三角形任意两边垂直平分线的交点,三边的垂直平分线
不必全部作出;
2.作图过程中,要注意保留作图痕迹;
3.注意写出结论.【跟踪训练】
4.如图,在平面直角坐标系中,点A,B,
C的坐标分别为(1,4),(5,4),(1,-2),
则△ABC外接圆的圆心坐标是( )
(A)(2,3) (B)(3,2)
(C)(1,3) (D)(3,1)
【解析】选D.作弦AB,AC的垂直平分线,交点即圆心,坐标是(3,1). 5.如图所示,一圆弧过方格的格点A,B,C,试在方格中建立平面
直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐
标是( )
(A)(-1,2) (B)(1,-1) (C)(-1,1) (D)(2,1)【解析】选C.如图所示,
∵AW=1,WH=3,∴
∵BQ=3,QH=1,∴
∴AH=BH,同理,AD=BD,所以GH为线
段AB的垂直平分线,易得EF为线段
AC的垂直平分线,H为圆的两条弦的垂直平分线的交点,则BH=
AH=HC,即H为圆心.于是该圆弧所在圆的圆心坐标是(-1,1).6.正方形的四个顶点和它的中心共5个点能确定______个不同的
圆.
【解析】正方形的四个顶点到它的中心的距离相等,中心与一边
的两个端点可以确定一个圆,正方形有四条边,因而有四个圆;
而正方形的四个顶点都在以中心为圆心的圆上,因而能确定5个
不同的圆.
答案:51.若⊙O的半径为5 cm,点A到圆心O的距离为
4 cm,那么点A与⊙O的位置关系是( )
(A)点A在圆外 (B)点A在圆上
(C)点A在圆内 (D)不能确定
【解析】选C. ∵AO=4 cm,半径为5 cm,∴点A在圆内.2.如图所示,A,B,C分别表示三个村庄,AB=
1 000米,BC=600米,AC=800米,在社会主义新
农村建设中,为了丰富群众生活,拟建一个文
化活动中心,要求这三个村庄到活动中心的距
离相等,则活动中心P的位置应在( )
(A)AB的中点 (B)BC的中点
(C)AC的中点 (D)C点【解析】选A.∵AB=1 000米,BC=600米,AC=800,∴AB2=BC2+AC2,
∴△ABC是直角三角形,∠C=90°.∵要求这三个村庄到活动中心
的距离相等,∴活动中心P的位置应在△ABC三边垂直平分线的交
点处,也就是△ABC的外心处.又∵△ABC是直角三角形,∴它的外
心在斜边AB的中点处,即为P点位置.3.在平面内,⊙O的半径为5 cm,点P到圆心O的距离为8 cm,则点
P与⊙O的位置关系是__________.
【解析】∵点P到圆心O的距离为8 cm,
∴d=8 cm,∵r=5 cm,则d>r,故点P在圆外.
答案:点P在圆外4.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标
为(4,4),则该圆弧所在圆的圆心坐标为_______.【解析】圆心是弦的垂直平分线的交点,可以作弦AB和BC的垂直平分线,交点即为圆心.如图所示,则圆心坐标是(2,0).
答案:(2,0)5.已知直线a和直线外的两点A,B,经过A,B作一圆,使它的圆心O
在直线a上.(不写作法,保留作图痕迹)【解析】如图所示
答:三种,点在_____,点在_____,点在_____.
2.过平面内一个点可以作多少个圆?圆心在哪里?
答:_____个.圆心分布在整个平面.圆内圆上圆外无数3.过平面内两点可以作多少个圆?圆心O在什么位置?
答:__________________________________________________
_____.
4.过平面内不在同一直线上的A,B,C 三点可以作多少个圆?圆
心在哪里?
答:过不在同一直线上的A,B,C三点能作_____圆,圆心是AB和BC
的___________的交点.
【点拨】不在同一条直线上的三个点确定一个圆.过两点可以画无数个圆,圆心在两点所连线段的垂直平分线上一个垂直平分线5.经过三角形三个顶点的圆叫做三角形的_______.三角形_______
的圆心叫做这个三角形的外心.这个三角形叫做这个圆的_______
_____.三角形的外心就是三角形三条边的___________的交点,它
到三角形_________的距离相等.
【点拨】三角形的外心与三角形的形状有关,锐角三角形的外心
在三角形的内部,直角三角形的外心是斜边的中点,钝角三角形
的外心在三角形的外部. 外接圆外接圆内接三角形垂直平分线三个顶点【预习思考】经过平面内A,B,C三点能否画圆?
提示:不一定.当A,B,C三点在一条直线上时,不能画圆;当
A,B,C三点不在一条直线上时,可以画一个圆. 点与圆的位置关系
【例1】Rt△ABC中,∠ACB=90°,CD⊥AB,AB=10,AC=6,以C点为圆
心,6为半径画圆,则点A,B,D与圆的位置关系是怎样的?【解题探究】
(1)确定点与圆的位置关系除了半径,还要知道什么?
答:还要知道点到圆心的距离.
(2)点A,B,D到圆心C的距离分别是哪些线段的长?
答:分别是线段CA,CB,CD的长.
(3)试求线段CB和CD的长.
答:在Rt△ACB中,AC=6,AB=10,由勾股定理可得:
BC=8;∵
∴CD=4.8.(4)说出点A,B,D与圆的位置关系.
答:∵AC=6,⊙C的半径r为6, AC=r,
∴ 点A在圆上.
∵CD=4.8,⊙C的半径r为6, DC<r,
∴点D在圆内.
∵BC=8,⊙C的半径r为6, BC>r,
∴点B在圆外.【互动探究】如何确定点与圆的位置关系?
提示:比较点到圆心的距离d与圆的半径r的大小. 若d=r,则点
在圆上;若d>r,则点在圆外;若d<r,则点在圆内,反之亦然.【规律总结】
判断点与圆的位置关系“二步法”
1.确定圆的半径及点到圆心的距离;
2.比较大小,确定位置关系.【跟踪训练】
1.已知⊙O的直径为10 cm,P为⊙O外的一点,则OP的长不可
能是( )
(A)12 cm (B)8 cm
(C)6 cm (D)5 cm
【解析】选D.因为直径为10 cm,则⊙O的半径为5 cm.而点P
在⊙O外,即OP>5 cm,故选D.2.已知矩形ABCD的边AB=6,AD=8.如果以点A为圆心作⊙A,使
B,C,D三点中在圆内和在圆外都至少有一个点,那么⊙A的半径r
的取值范围是( )
(A)6<r<10 (B)8<r<10
(C)6<r≤8 (D)8<r≤10
【解析】选A.∵AB=6,AD=8,∴AC=10,
∴点C一定在圆外,点B一定在圆内,
∴⊙A的半径r的取值范围是6<r<10.3.已知点P到⊙O的最近距离为3 cm,最远距离为9 cm,求⊙O的
半径.
【解析】∵点P到⊙O的最近距离为3 cm,最远距离为9 cm,则当
点P在圆外时,⊙O的直径是9-3=6(cm),半径是3 cm;当点P在圆
内时,⊙O的直径是9+3=12(cm),半径为6 cm.
∴⊙O的半径为3 cm或6 cm. 确定圆的条件
【例2】(6分)如图所示,破残的圆形轮
片上,弦AB的垂直平分线交弧AB于点C,
交弦AB于点D.已知:AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆;(不写作法,
保留作图痕迹)
(2)求(1)中所作圆的半径.
特别提醒:圆心是弦的垂直平分线的交点. 【规范解答】
(1)连结AC,作弦AC的垂直平分线与弦AB的垂直平分线交于O点,
以O为圆心,OB长为半径作圆O,圆O就是此残片所在的圆,如图.
………………………………………3分(2)连结OB,设OB=x,BD=12 cm,OD=(x-8) cm,
则根据勾股定理列方程:x2=122+(x-8)2,……………………5分
解得:x=13.
答:圆的半径为13 cm.………………………………………6分【互动探究】1.作圆的关键是什么?
提示:作圆的关键是确定圆心的位置和半径的大小.
2.三角形有几个外接圆?
提示:任意一个三角形都有且只有一个外接圆.【规律总结】
作三角形外接圆时需注意的三个问题
1.圆心是三角形任意两边垂直平分线的交点,三边的垂直平分线
不必全部作出;
2.作图过程中,要注意保留作图痕迹;
3.注意写出结论.【跟踪训练】
4.如图,在平面直角坐标系中,点A,B,
C的坐标分别为(1,4),(5,4),(1,-2),
则△ABC外接圆的圆心坐标是( )
(A)(2,3) (B)(3,2)
(C)(1,3) (D)(3,1)
【解析】选D.作弦AB,AC的垂直平分线,交点即圆心,坐标是(3,1). 5.如图所示,一圆弧过方格的格点A,B,C,试在方格中建立平面
直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐
标是( )
(A)(-1,2) (B)(1,-1) (C)(-1,1) (D)(2,1)【解析】选C.如图所示,
∵AW=1,WH=3,∴
∵BQ=3,QH=1,∴
∴AH=BH,同理,AD=BD,所以GH为线
段AB的垂直平分线,易得EF为线段
AC的垂直平分线,H为圆的两条弦的垂直平分线的交点,则BH=
AH=HC,即H为圆心.于是该圆弧所在圆的圆心坐标是(-1,1).6.正方形的四个顶点和它的中心共5个点能确定______个不同的
圆.
【解析】正方形的四个顶点到它的中心的距离相等,中心与一边
的两个端点可以确定一个圆,正方形有四条边,因而有四个圆;
而正方形的四个顶点都在以中心为圆心的圆上,因而能确定5个
不同的圆.
答案:51.若⊙O的半径为5 cm,点A到圆心O的距离为
4 cm,那么点A与⊙O的位置关系是( )
(A)点A在圆外 (B)点A在圆上
(C)点A在圆内 (D)不能确定
【解析】选C. ∵AO=4 cm,半径为5 cm,∴点A在圆内.2.如图所示,A,B,C分别表示三个村庄,AB=
1 000米,BC=600米,AC=800米,在社会主义新
农村建设中,为了丰富群众生活,拟建一个文
化活动中心,要求这三个村庄到活动中心的距
离相等,则活动中心P的位置应在( )
(A)AB的中点 (B)BC的中点
(C)AC的中点 (D)C点【解析】选A.∵AB=1 000米,BC=600米,AC=800,∴AB2=BC2+AC2,
∴△ABC是直角三角形,∠C=90°.∵要求这三个村庄到活动中心
的距离相等,∴活动中心P的位置应在△ABC三边垂直平分线的交
点处,也就是△ABC的外心处.又∵△ABC是直角三角形,∴它的外
心在斜边AB的中点处,即为P点位置.3.在平面内,⊙O的半径为5 cm,点P到圆心O的距离为8 cm,则点
P与⊙O的位置关系是__________.
【解析】∵点P到圆心O的距离为8 cm,
∴d=8 cm,∵r=5 cm,则d>r,故点P在圆外.
答案:点P在圆外4.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标
为(4,4),则该圆弧所在圆的圆心坐标为_______.【解析】圆心是弦的垂直平分线的交点,可以作弦AB和BC的垂直平分线,交点即为圆心.如图所示,则圆心坐标是(2,0).
答案:(2,0)5.已知直线a和直线外的两点A,B,经过A,B作一圆,使它的圆心O
在直线a上.(不写作法,保留作图痕迹)【解析】如图所示
