2020春华师版九下数学 27.3.1弧长和扇形的面积课件(30张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.3.1弧长和扇形的面积课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 965.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:11:03 | ||
图片预览










文档简介
课件30张PPT。1.弧长和扇形的面积 1.弧长:圆的周长可以看作____度的圆心角所对的弧.设圆的半
径为r,则1°的圆心角所对的弧长l是______,2°的圆心角所对
的弧长l是_____,4°的圆心角所对的弧长l是_____,…,n°的
圆心角所对的弧长l是_____.3602.什么叫扇形?
答:由组成圆心角的两条_____和圆心角所对的___所围成的图
形叫做扇形.
3.扇形的面积:圆的面积可以看作____度圆心角所对的扇形的
面积.设圆的半径为r,1°的圆心角所对的扇形面积S扇形 ,
2°的圆心角所对的扇形面积S扇形= ,5°的圆心角所对的扇形面积S扇形= ,n°的圆心角所对的扇形面积S扇形= .半径弧360__________________【点拨】半径一定时,圆心角越大,弧长和扇形的面积也越大;
圆心角一定时,半径越大,弧长和扇形的面积也越大.
【预习思考】弧长、扇形面积与什么有关?
提示:弧长、扇形的面积与所在圆的半径和所对的圆心角有
关. 弧长公式的应用
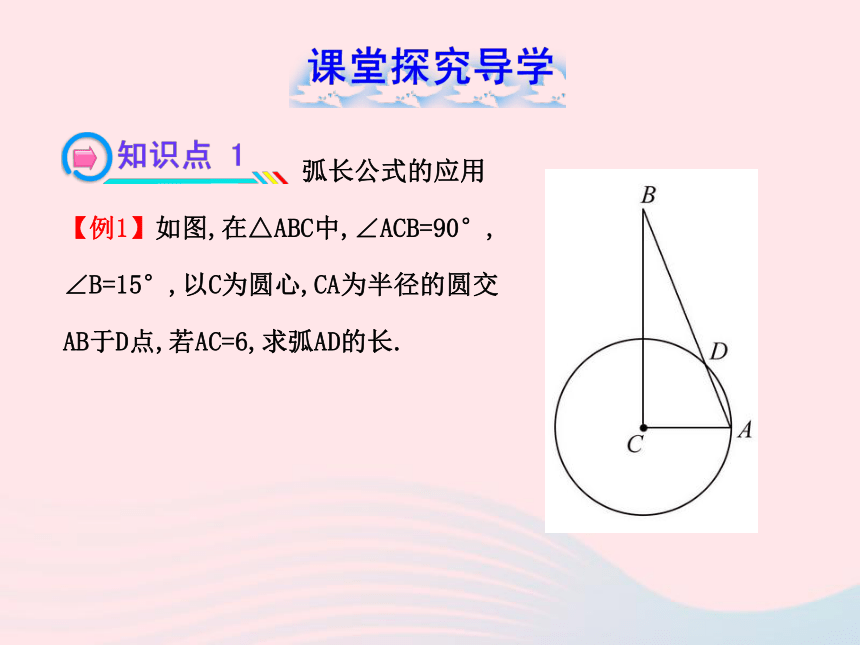
【例1】如图,在△ABC中,∠ACB=90°,
∠B=15°,以C为圆心,CA为半径的圆交
AB于D点,若AC=6,求弧AD的长.【解题探究】
①试比较∠CAD与∠CDA的大小.
答:连结CD,∵AC=CD,∴∠CAD=∠CDA.
②∠ACD为多少度?
答:∵∠ACB=90°,∠B=15°,∴∠CAD=75°,
∴∠ACD=30°.
③ 的长度为多少?
答:∵AC=6,∴ 的长度=【互动探究】利用弧长公式进行有关弧长的计算时应注意什么
问题?
提示:①弧长公式 中,n是表示“1°”的倍数,它和
“180”都不带单位;②已知l,n,r中的任意两个量,都可以求出
第三个量.【规律总结】
求弧长“三步法”
1.求弧所对圆心角的度数;
2.求弧所在圆的半径;
3.依据弧长公式求出弧长.【跟踪训练】
1.一个扇形的圆心角为60°,它所对的弧长
为2π cm,则这个扇形的半径为( )
(A)6 cm (B)12 cm (C) (D)
【解析】选A.由扇形的圆心角为60°,它所对的弧长为2πcm,
即n=60,l=2π,
根据弧长公式2.在半径为6 cm的圆中,60°的圆心角所对的
弧长等于______.
【解析】方法一:直接利用弧长计算公式:
方法二:圆心角为60°,所以圆心角所夹的扇形为圆的 ,因此
弧长为圆周长的 ,即
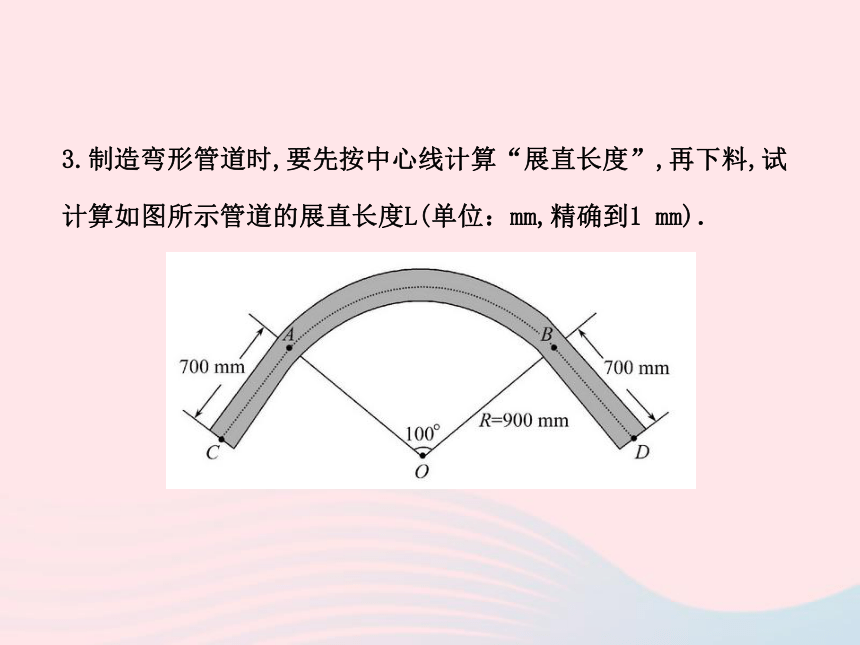
答案:2πcm3.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试
计算如图所示管道的展直长度L(单位:mm,精确到1 mm).【解析】由弧长公式,可得弧AB的长
=500π≈1 570(mm)
因此所要求的展直长度
L=2×700+1 570=2 970(mm)
答:管道的展直长度为2 970 mm. 扇形面积的计算
【例2】如图,
△ABC和△ABD都是⊙O的内接三角形,
圆心O在边AB上,边AD分别与BC,OC交
于E,F两点,点C为 的中点.
(1)求证:OF∥BD;
(2)若 ,且⊙O的半径R=6 cm.
①求证:点F为线段OC的中点;②求圆中阴影部分(弓形)的面积.【规范解答】(1)∵OC为半径,点C为 的中点,
∴OC⊥AD.……………………………………………………1分
∵AB为直径,∴∠BDA=90°,BD⊥AD,
∴OF∥BD.……………………………………………………2分
(2)①∵O为AB的中点,OF∥BD,
∴F为AD的中点,
∴FO= .………………………………3分∵FC∥BD,∴∠FCE=∠DBE.
∵∠FEC=∠DEB,∴△ECF∽△EBD…………………………4分
…………………………………5分
∴FC=FO,即点F为CO的中点.………………………………6分
②∵FC=FO,OC⊥AD,∴AC=AO.
又∵AO=CO,∴△AOC为等边三角形.…………………………7分
∴S阴= ……………8分【互动探究】比较扇形面积公式和弧长公式,如何用弧长l表示
扇形的面积?
提示:【规律总结】
利用扇形面积公式的两点注意
1.公式中的n与180不带单位;
2.已知半径和圆心角求扇形面积时,通常选用公式
已知半径和弧长时,一般采用公式S扇形= lr.【跟踪训练】
4.如图,直径AB为6的
半圆,绕A点逆时针旋转60°,此时点B到
了点B′,则图中阴影部分的面积是( )
(A)3π (B)6π
(C)5π (D)4π
【解析】选B.由图可得,阴影部分的面积即为扇形BAB′的面
积,所以图中阴影部分的面积是5.如图,水平放着的圆柱形排水管的截面半径是12 cm,其中水面
高度为6 cm,求截面上有水的弓形面积.【解析】连结OA,OB.
∵OE=OC-CE=12-6=6 (cm),在直角△AOE中,
OA=12 cm,OE=6 cm,∴∠OAE=30°,
AE=OA·cos 30°= (cm).
∴∠AOB=2∠AOE=120°,AB=2AE= cm.
∴扇形AOB的面积为 =48π(cm2).
△AOB的面积为
则阴影部分的面积为【变式备选】如图,水平放着的圆柱形排水管的截面直径为
1 000 mm,其中水面宽AB=800 mm,则水的最大深度为______mm.【解析】过O点作OC⊥AB,C为垂足,交⊙O于D,连结OA,如图所示.
由题意知OA=OD=500 mm,AB=800 mm,
∵OC⊥AB,∴AC=BC=400 mm,
在Rt△AOC中,OA2=AC2+OC2,
∴CD=OC+OD=800(mm),即水的最大深度为800 mm.
答案:8001.如果一个扇形的半径是1,弧长是 ,那么
此扇形的圆心角的大小为( )
(A)30° (B)45° (C)60° (D)90°
【解析】选C.根据弧长公式 可得 解得n=60.2.如图所示,扇形
AOB的圆心角为120°,半径为2,则
图中阴影部分的面积为( )
(A) (B)
(C) (D)【解析】选A.作OC⊥AB,
∵∠AOB=120°,
∴∠OAB=30°.
∵OA=2,∴OC=1,AC= 即AB=
阴影部分的面积为3.如图,正方形的边长为
2,以各边为直径在正方形内画半圆,则图
中阴影部分的面积为_____.(结果保留两位
有效数字,参考数据:π=3.14)
【解析】阴影部分的面积=正方形的面积-(4× π·12-22)
=4-2π+4=8-6.28≈1.7.
答案:1.74.如图,在Rt△ABC
中,∠ABC=90°, AB=8 cm , BC=6 cm ,
分别以A,C为圆心,以 的长为半径作圆,
将 Rt△ABC截去两个扇形,则剩余(阴影)
部分的面积为_________cm2(结果保留π).【解析】阴影部分的面积等于Rt△ABC的面积减去以A,C为圆心
的两个扇形的面积,两个扇形的圆心角之和等于90°,由勾股定
理得AC=10 cm,半径为5 cm. S阴影=
答案:5.如图,两个同心圆的半径所截得的弧长
AB=6π cm,弧长CD=10π cm,且AC=12 cm.
(1)求两圆的半径长.
(2)阴影部分的面积是多少?【解析】(1)设OA=r,则OC=r+12,扇形的圆心角是n度.
根据题意得:
解得:n=60,r=18(cm),
∴r+12=30(cm),即两圆的半径长分别是18 cm,30 cm;
(2)阴影部分的面积是
径为r,则1°的圆心角所对的弧长l是______,2°的圆心角所对
的弧长l是_____,4°的圆心角所对的弧长l是_____,…,n°的
圆心角所对的弧长l是_____.3602.什么叫扇形?
答:由组成圆心角的两条_____和圆心角所对的___所围成的图
形叫做扇形.
3.扇形的面积:圆的面积可以看作____度圆心角所对的扇形的
面积.设圆的半径为r,1°的圆心角所对的扇形面积S扇形 ,
2°的圆心角所对的扇形面积S扇形= ,5°的圆心角所对的扇形面积S扇形= ,n°的圆心角所对的扇形面积S扇形= .半径弧360__________________【点拨】半径一定时,圆心角越大,弧长和扇形的面积也越大;
圆心角一定时,半径越大,弧长和扇形的面积也越大.
【预习思考】弧长、扇形面积与什么有关?
提示:弧长、扇形的面积与所在圆的半径和所对的圆心角有
关. 弧长公式的应用
【例1】如图,在△ABC中,∠ACB=90°,
∠B=15°,以C为圆心,CA为半径的圆交
AB于D点,若AC=6,求弧AD的长.【解题探究】
①试比较∠CAD与∠CDA的大小.
答:连结CD,∵AC=CD,∴∠CAD=∠CDA.
②∠ACD为多少度?
答:∵∠ACB=90°,∠B=15°,∴∠CAD=75°,
∴∠ACD=30°.
③ 的长度为多少?
答:∵AC=6,∴ 的长度=【互动探究】利用弧长公式进行有关弧长的计算时应注意什么
问题?
提示:①弧长公式 中,n是表示“1°”的倍数,它和
“180”都不带单位;②已知l,n,r中的任意两个量,都可以求出
第三个量.【规律总结】
求弧长“三步法”
1.求弧所对圆心角的度数;
2.求弧所在圆的半径;
3.依据弧长公式求出弧长.【跟踪训练】
1.一个扇形的圆心角为60°,它所对的弧长
为2π cm,则这个扇形的半径为( )
(A)6 cm (B)12 cm (C) (D)
【解析】选A.由扇形的圆心角为60°,它所对的弧长为2πcm,
即n=60,l=2π,
根据弧长公式2.在半径为6 cm的圆中,60°的圆心角所对的
弧长等于______.
【解析】方法一:直接利用弧长计算公式:
方法二:圆心角为60°,所以圆心角所夹的扇形为圆的 ,因此
弧长为圆周长的 ,即
答案:2πcm3.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试
计算如图所示管道的展直长度L(单位:mm,精确到1 mm).【解析】由弧长公式,可得弧AB的长
=500π≈1 570(mm)
因此所要求的展直长度
L=2×700+1 570=2 970(mm)
答:管道的展直长度为2 970 mm. 扇形面积的计算
【例2】如图,
△ABC和△ABD都是⊙O的内接三角形,
圆心O在边AB上,边AD分别与BC,OC交
于E,F两点,点C为 的中点.
(1)求证:OF∥BD;
(2)若 ,且⊙O的半径R=6 cm.
①求证:点F为线段OC的中点;②求圆中阴影部分(弓形)的面积.【规范解答】(1)∵OC为半径,点C为 的中点,
∴OC⊥AD.……………………………………………………1分
∵AB为直径,∴∠BDA=90°,BD⊥AD,
∴OF∥BD.……………………………………………………2分
(2)①∵O为AB的中点,OF∥BD,
∴F为AD的中点,
∴FO= .………………………………3分∵FC∥BD,∴∠FCE=∠DBE.
∵∠FEC=∠DEB,∴△ECF∽△EBD…………………………4分
…………………………………5分
∴FC=FO,即点F为CO的中点.………………………………6分
②∵FC=FO,OC⊥AD,∴AC=AO.
又∵AO=CO,∴△AOC为等边三角形.…………………………7分
∴S阴= ……………8分【互动探究】比较扇形面积公式和弧长公式,如何用弧长l表示
扇形的面积?
提示:【规律总结】
利用扇形面积公式的两点注意
1.公式中的n与180不带单位;
2.已知半径和圆心角求扇形面积时,通常选用公式
已知半径和弧长时,一般采用公式S扇形= lr.【跟踪训练】
4.如图,直径AB为6的
半圆,绕A点逆时针旋转60°,此时点B到
了点B′,则图中阴影部分的面积是( )
(A)3π (B)6π
(C)5π (D)4π
【解析】选B.由图可得,阴影部分的面积即为扇形BAB′的面
积,所以图中阴影部分的面积是5.如图,水平放着的圆柱形排水管的截面半径是12 cm,其中水面
高度为6 cm,求截面上有水的弓形面积.【解析】连结OA,OB.
∵OE=OC-CE=12-6=6 (cm),在直角△AOE中,
OA=12 cm,OE=6 cm,∴∠OAE=30°,
AE=OA·cos 30°= (cm).
∴∠AOB=2∠AOE=120°,AB=2AE= cm.
∴扇形AOB的面积为 =48π(cm2).
△AOB的面积为
则阴影部分的面积为【变式备选】如图,水平放着的圆柱形排水管的截面直径为
1 000 mm,其中水面宽AB=800 mm,则水的最大深度为______mm.【解析】过O点作OC⊥AB,C为垂足,交⊙O于D,连结OA,如图所示.
由题意知OA=OD=500 mm,AB=800 mm,
∵OC⊥AB,∴AC=BC=400 mm,
在Rt△AOC中,OA2=AC2+OC2,
∴CD=OC+OD=800(mm),即水的最大深度为800 mm.
答案:8001.如果一个扇形的半径是1,弧长是 ,那么
此扇形的圆心角的大小为( )
(A)30° (B)45° (C)60° (D)90°
【解析】选C.根据弧长公式 可得 解得n=60.2.如图所示,扇形
AOB的圆心角为120°,半径为2,则
图中阴影部分的面积为( )
(A) (B)
(C) (D)【解析】选A.作OC⊥AB,
∵∠AOB=120°,
∴∠OAB=30°.
∵OA=2,∴OC=1,AC= 即AB=
阴影部分的面积为3.如图,正方形的边长为
2,以各边为直径在正方形内画半圆,则图
中阴影部分的面积为_____.(结果保留两位
有效数字,参考数据:π=3.14)
【解析】阴影部分的面积=正方形的面积-(4× π·12-22)
=4-2π+4=8-6.28≈1.7.
答案:1.74.如图,在Rt△ABC
中,∠ABC=90°, AB=8 cm , BC=6 cm ,
分别以A,C为圆心,以 的长为半径作圆,
将 Rt△ABC截去两个扇形,则剩余(阴影)
部分的面积为_________cm2(结果保留π).【解析】阴影部分的面积等于Rt△ABC的面积减去以A,C为圆心
的两个扇形的面积,两个扇形的圆心角之和等于90°,由勾股定
理得AC=10 cm,半径为5 cm. S阴影=
答案:5.如图,两个同心圆的半径所截得的弧长
AB=6π cm,弧长CD=10π cm,且AC=12 cm.
(1)求两圆的半径长.
(2)阴影部分的面积是多少?【解析】(1)设OA=r,则OC=r+12,扇形的圆心角是n度.
根据题意得:
解得:n=60,r=18(cm),
∴r+12=30(cm),即两圆的半径长分别是18 cm,30 cm;
(2)阴影部分的面积是
