人教版七年级数学下册 7.2坐标方法的简单应用课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学下册 7.2坐标方法的简单应用课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 16:42:56 | ||
图片预览




文档简介
(共20张PPT)
7.2 坐标方法的简单应用
展示交流1
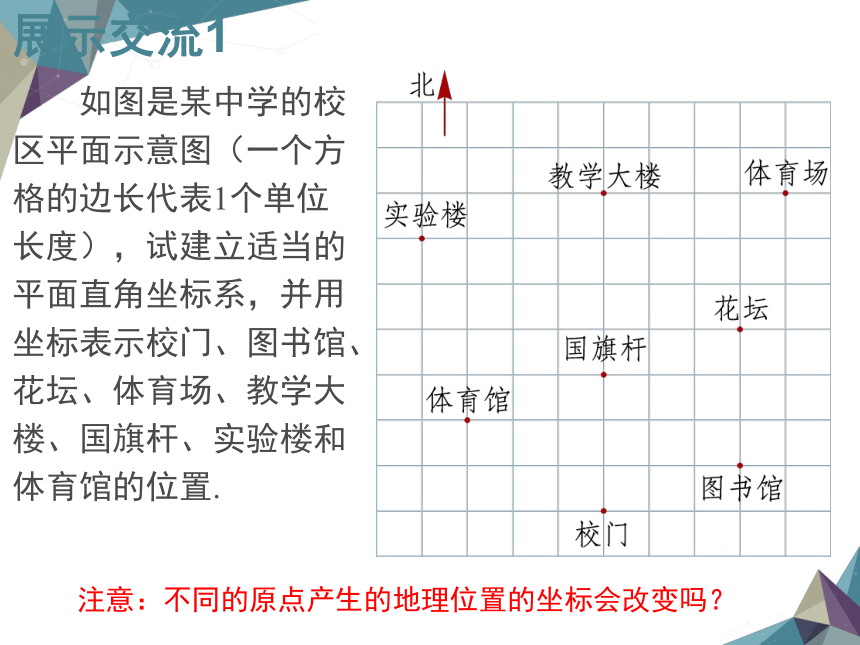
如图是某中学的校区平面示意图(一个方格的边长代表1个单位长度),试建立适当的平面直角坐标系,并用坐标表示校门、图书馆、花坛、体育场、教学大楼、国旗杆、实验楼和体育馆的位置.
注意:不同的原点产生的地理位置的坐标会改变吗?
解:如图所示,建立平面直角坐标系.
校门(0,0),
图书馆(3,1),
花坛(3,4),
体育场(4,7),
教学大楼(0,7),
国旗杆(0,3),
实验楼(-4,6),
体育馆(-3,2).
变式:如图是某中学的校区平面示意图(一个方格的边长代表1个单位长度),花坛的位置用(5,2)表示,请建立平面直角坐标系,并用坐标表示校门、图书馆、体育场、教学大楼、国旗杆、实验楼和体育馆的位置.
思考: 我们知道,通过建立平面直角坐标系,可以用坐标表示平面内点的位置。还有其他方法吗?
用方向和距离表示地理位置
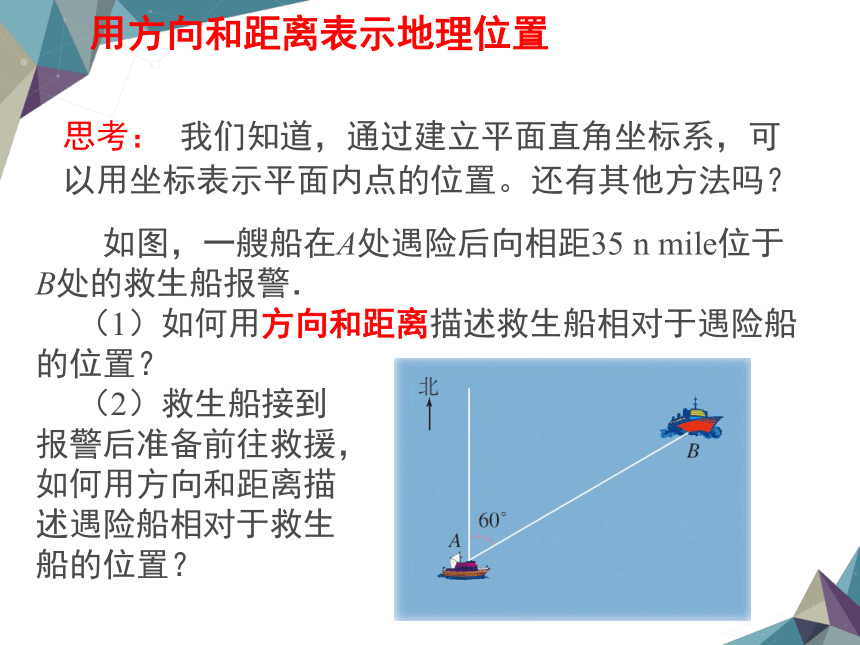
如图,一艘船在A处遇险后向相距35 n mile位于B处的救生船报警.
(1)如何用方向和距离描述救生船相对于遇险船的位置?
(2)救生船接到
报警后准备前往救援,
如何用方向和距离描
述遇险船相对于救生
船的位置?
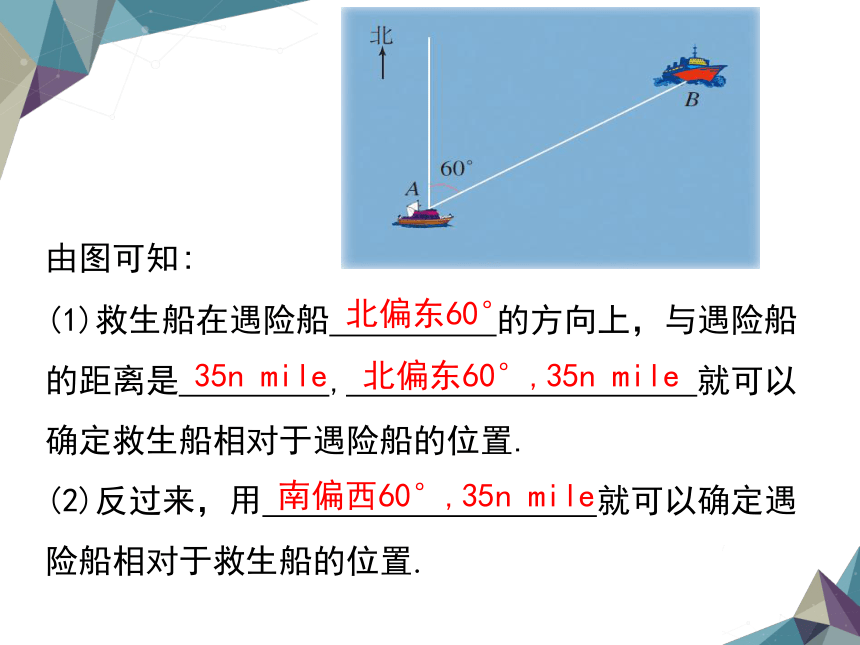
由图可知:
(1)救生船在遇险船 的方向上,与遇险船的距离是 , 就可以确定救生船相对于遇险船的位置.
(2)反过来,用 就可以确定遇险船相对于救生船的位置.
北偏东60°
35n mile
北偏东60°,35n mile
南偏西60°,35n mile
展示交流2
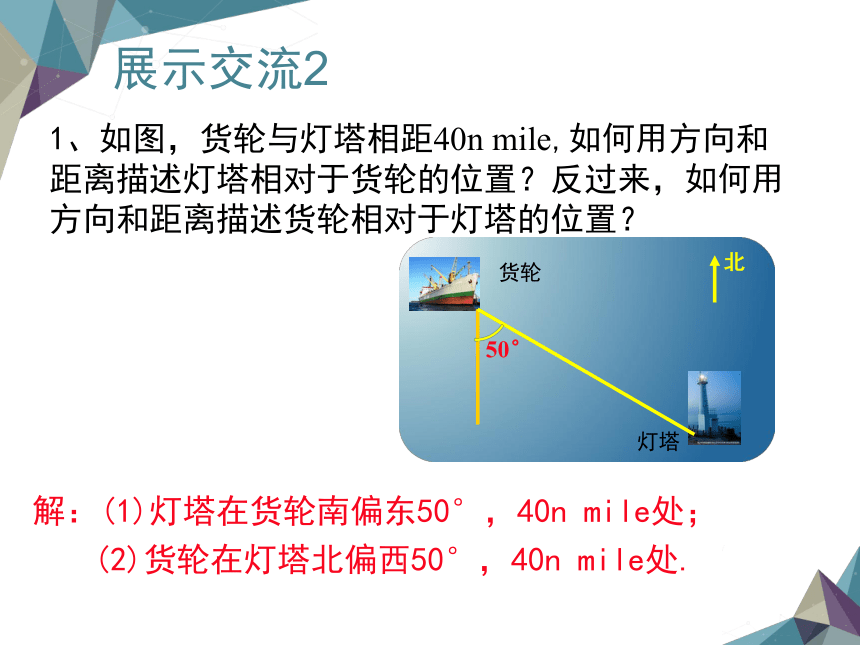
1、如图,货轮与灯塔相距40n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
解:(1)灯塔在货轮南偏东50°,40n mile处;
(2)货轮在灯塔北偏西50°,40n mile处.
货轮
灯塔
2、
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
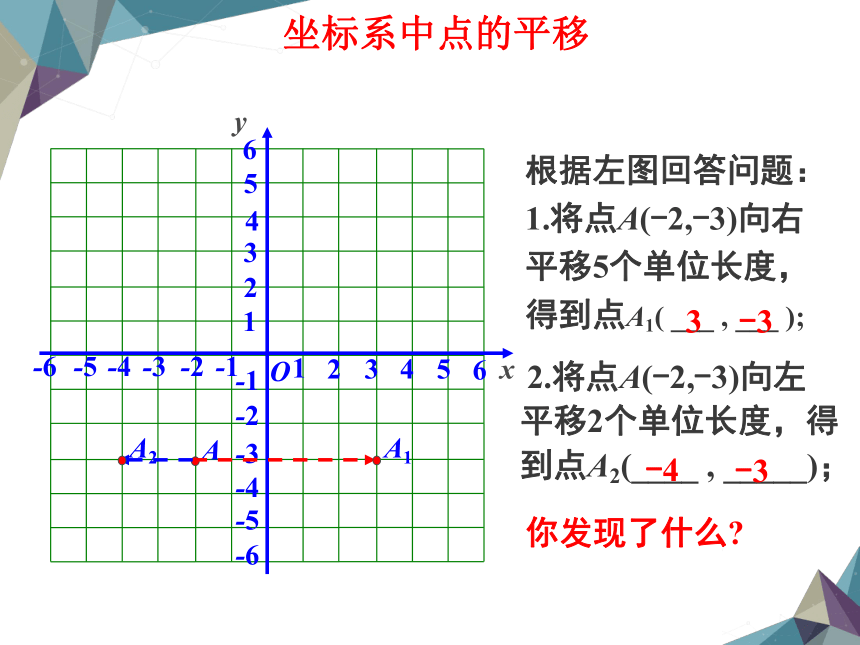
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移2个单位长度,得到点A2(____ , _____);
-4
-3
3
-3
你发现了什么?
y
x
坐标系中点的平移
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
-2
1
-2
-5
你发现了什么?
y
x
(1)左、右平移:
(2)上、下平移:
点(x,y)
点(x,y)
(x+a,y)
(x-a,y)
点(x,y)
点(x,y)
(x,y+b)
(x,y-b)
点在平面直角坐标系中的平移规律
横坐标不变,上加下减
纵坐标不变,左减右加
1.将点A(3,2)向上平移2个单位长度,再向左平移3个单位得到A1,则A1的坐标 为______.
2.将点A(3,2)向下平移3个单位长度,再向右平移4个单位得到A2,则 A2的坐标为______.
3.将点A(3,2)向左平移4个单位长度,再向下平移3个单位得到A3,则A3的坐标为______.
(0,4)
4.点A1(6,3)是由点A(-2,5)经过 ,
得到的.
向右平移8个单位长度
向下平移2个单位长度
(7,-1)
(-1,-1)
展示交流3
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
1、如图,△ ABC在坐标平面内平移后得到△A1B1C1.
(1)如何平移到△A1B1C1?
(2)写出△ ABC与△ A1B1C1各点的坐标,它们有怎样的变化?
-3
-2
-1
O
1
2
3
4
x
向右平移5个单位;
A(-1,3),B(-4,2), C(-2,1),
A1(4,3),B1(1,2), C1(3,1);
平移后的对应点的横坐标增加了5,纵坐标不变;
坐标系中图形的平移
A2(4,-1),B2(1,-2),C2(3,-3);
平移后的对应点的横坐标不变,纵坐标减少了4.
(3)如果△A1B1C1向下平移4个单位,得到△ A2B2C2,写出各点的坐标,它们有怎样的变化?
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
A2
C2
B2
-3
-2
-1
O
1
2
3
4
x
(1)左、右平移:
(2)上、下平移:
原图形上的点(x,y)
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
横坐标不变,上加下减
纵坐标不变,左减右加
原图形上的点(x,y)
原图形上的点(x,y)
原图形上的点(x,y)
图形在平面直角坐标系中的平移规律
1.三角形ABC中,BC边上的中点为M,把三角形 ABC向右平移2个单位长度,再向下平移3个单位长度后,得到三角形A1B1C1. 边B1C1的中点M1的坐标为(-1,0),则点M 的坐标为 .
2.已知三角形ABC, A(-3,2),B(1,1),C(-1,-2),现将三角形ABC平移,使点A到点(1,-2) 的位置上,则点B,C的坐标分别为 , .
展示交流4
(5,-3)
(3,-6)
(-3, 3)
3.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
1
y
O
1
x
A
B
C
A1
B1
C1
解:(1)△A1B1C1如图所示,各点的坐标分别为A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
(2)求出以A、C、A1、C1为顶点的四边形的面积.
P
小结
一、表示物体的地理位置的方法
(1)用坐标表示物体的地理位置;
(2)用方向和距离表示物体的地理位置;
二、用坐标表示平移
(1)坐标系中点的平移;
(2)坐标系中图形的平移.
巩固练习
1、
2、
3、
作业布置
1.课本P79 第6、8题
2.《作业》P35-38
7.2 坐标方法的简单应用
展示交流1
如图是某中学的校区平面示意图(一个方格的边长代表1个单位长度),试建立适当的平面直角坐标系,并用坐标表示校门、图书馆、花坛、体育场、教学大楼、国旗杆、实验楼和体育馆的位置.
注意:不同的原点产生的地理位置的坐标会改变吗?
解:如图所示,建立平面直角坐标系.
校门(0,0),
图书馆(3,1),
花坛(3,4),
体育场(4,7),
教学大楼(0,7),
国旗杆(0,3),
实验楼(-4,6),
体育馆(-3,2).
变式:如图是某中学的校区平面示意图(一个方格的边长代表1个单位长度),花坛的位置用(5,2)表示,请建立平面直角坐标系,并用坐标表示校门、图书馆、体育场、教学大楼、国旗杆、实验楼和体育馆的位置.
思考: 我们知道,通过建立平面直角坐标系,可以用坐标表示平面内点的位置。还有其他方法吗?
用方向和距离表示地理位置
如图,一艘船在A处遇险后向相距35 n mile位于B处的救生船报警.
(1)如何用方向和距离描述救生船相对于遇险船的位置?
(2)救生船接到
报警后准备前往救援,
如何用方向和距离描
述遇险船相对于救生
船的位置?
由图可知:
(1)救生船在遇险船 的方向上,与遇险船的距离是 , 就可以确定救生船相对于遇险船的位置.
(2)反过来,用 就可以确定遇险船相对于救生船的位置.
北偏东60°
35n mile
北偏东60°,35n mile
南偏西60°,35n mile
展示交流2
1、如图,货轮与灯塔相距40n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
解:(1)灯塔在货轮南偏东50°,40n mile处;
(2)货轮在灯塔北偏西50°,40n mile处.
货轮
灯塔
2、
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移2个单位长度,得到点A2(____ , _____);
-4
-3
3
-3
你发现了什么?
y
x
坐标系中点的平移
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
-2
1
-2
-5
你发现了什么?
y
x
(1)左、右平移:
(2)上、下平移:
点(x,y)
点(x,y)
(x+a,y)
(x-a,y)
点(x,y)
点(x,y)
(x,y+b)
(x,y-b)
点在平面直角坐标系中的平移规律
横坐标不变,上加下减
纵坐标不变,左减右加
1.将点A(3,2)向上平移2个单位长度,再向左平移3个单位得到A1,则A1的坐标 为______.
2.将点A(3,2)向下平移3个单位长度,再向右平移4个单位得到A2,则 A2的坐标为______.
3.将点A(3,2)向左平移4个单位长度,再向下平移3个单位得到A3,则A3的坐标为______.
(0,4)
4.点A1(6,3)是由点A(-2,5)经过 ,
得到的.
向右平移8个单位长度
向下平移2个单位长度
(7,-1)
(-1,-1)
展示交流3
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
1、如图,△ ABC在坐标平面内平移后得到△A1B1C1.
(1)如何平移到△A1B1C1?
(2)写出△ ABC与△ A1B1C1各点的坐标,它们有怎样的变化?
-3
-2
-1
O
1
2
3
4
x
向右平移5个单位;
A(-1,3),B(-4,2), C(-2,1),
A1(4,3),B1(1,2), C1(3,1);
平移后的对应点的横坐标增加了5,纵坐标不变;
坐标系中图形的平移
A2(4,-1),B2(1,-2),C2(3,-3);
平移后的对应点的横坐标不变,纵坐标减少了4.
(3)如果△A1B1C1向下平移4个单位,得到△ A2B2C2,写出各点的坐标,它们有怎样的变化?
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
A2
C2
B2
-3
-2
-1
O
1
2
3
4
x
(1)左、右平移:
(2)上、下平移:
原图形上的点(x,y)
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
横坐标不变,上加下减
纵坐标不变,左减右加
原图形上的点(x,y)
原图形上的点(x,y)
原图形上的点(x,y)
图形在平面直角坐标系中的平移规律
1.三角形ABC中,BC边上的中点为M,把三角形 ABC向右平移2个单位长度,再向下平移3个单位长度后,得到三角形A1B1C1. 边B1C1的中点M1的坐标为(-1,0),则点M 的坐标为 .
2.已知三角形ABC, A(-3,2),B(1,1),C(-1,-2),现将三角形ABC平移,使点A到点(1,-2) 的位置上,则点B,C的坐标分别为 , .
展示交流4
(5,-3)
(3,-6)
(-3, 3)
3.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
1
y
O
1
x
A
B
C
A1
B1
C1
解:(1)△A1B1C1如图所示,各点的坐标分别为A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
(2)求出以A、C、A1、C1为顶点的四边形的面积.
P
小结
一、表示物体的地理位置的方法
(1)用坐标表示物体的地理位置;
(2)用方向和距离表示物体的地理位置;
二、用坐标表示平移
(1)坐标系中点的平移;
(2)坐标系中图形的平移.
巩固练习
1、
2、
3、
作业布置
1.课本P79 第6、8题
2.《作业》P35-38
