人教版初中数学八年级下册17.1.1《勾股定理》课件(24张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册17.1.1《勾股定理》课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
勾股定理
古希腊著名数学家毕达哥拉斯
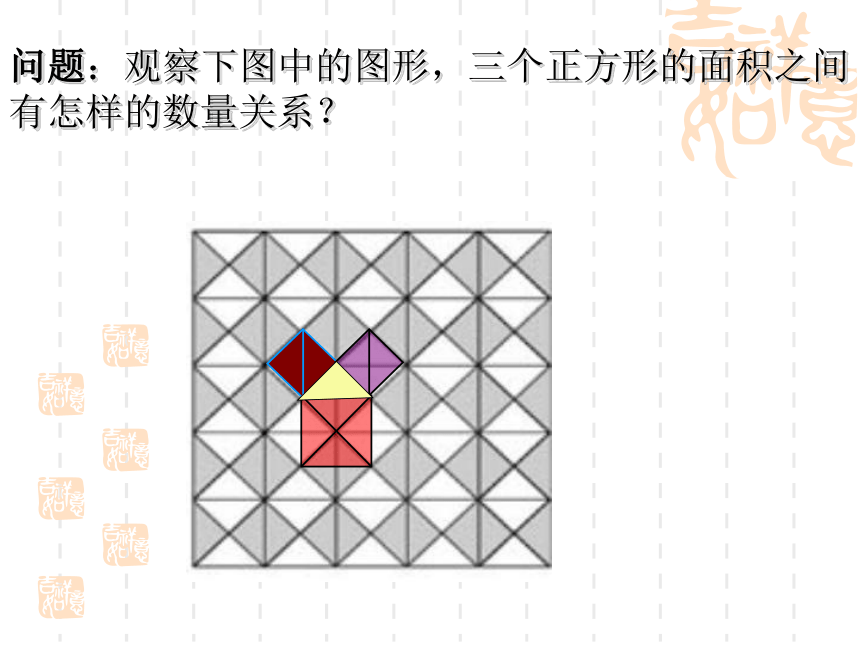
问题:观察下图中的图形,三个正方形的面积之间有怎样的数量关系?
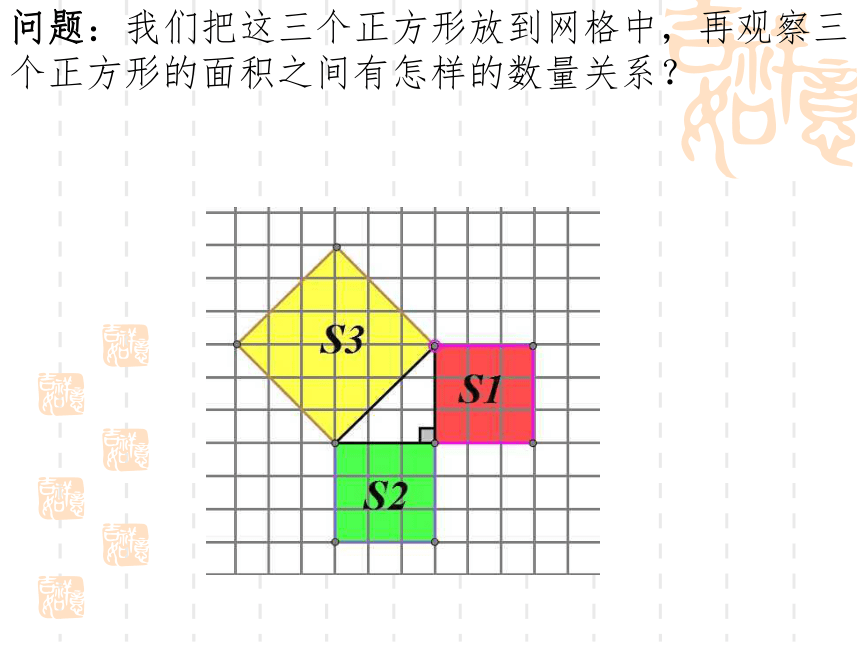
问题:我们把这三个正方形放到网格中,再观察三个正方形的面积之间有怎样的数量关系?
问题:当我们把图形改变,你能发现三个正方形的面积之间的数量关系吗?
?
命题
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
《勾股圆方图》
∵ c2= 4? ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab/2+(b- a)2
数学史话
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现:勾股定理
勾股定理
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
1、已知ΔABC中,∠C=90?,若a=6, b=8, 则c=_________
2、已知ΔABC中,∠C=90?,若a=5, c=13, 则b=_________
3、直角三角形的两条边为3和4,求这个直角三角形的第三边的长。
例题:在波平如镜的湖面上,有一朵美丽的水莲 ,它高出水面1米? ,一阵大风吹过,水莲被吹至一边,花朵齐及水面,如果知道水莲移动的水平距离为2米 ,问这里水深多少?
实践应用
DA
C
B
D
B
A
例题:它高出水面1米? , 水莲被吹至一边,花朵齐及水面,如果知道水莲移动的水平距离为2米 ,问这里水深多少?
谈谈你的收获!
1.完成课本习题1、2、3(必做)
2.课后小实验:如图,分别以直角三角形的三 边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么? (必做)
3.做一棵奇妙的勾股树(选做)
作业快餐:
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3)????
勾股定理
古希腊著名数学家毕达哥拉斯
问题:观察下图中的图形,三个正方形的面积之间有怎样的数量关系?
问题:我们把这三个正方形放到网格中,再观察三个正方形的面积之间有怎样的数量关系?
问题:当我们把图形改变,你能发现三个正方形的面积之间的数量关系吗?
?
命题
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
《勾股圆方图》
∵ c2= 4? ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab/2+(b- a)2
数学史话
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现:勾股定理
勾股定理
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
1、已知ΔABC中,∠C=90?,若a=6, b=8, 则c=_________
2、已知ΔABC中,∠C=90?,若a=5, c=13, 则b=_________
3、直角三角形的两条边为3和4,求这个直角三角形的第三边的长。
例题:在波平如镜的湖面上,有一朵美丽的水莲 ,它高出水面1米? ,一阵大风吹过,水莲被吹至一边,花朵齐及水面,如果知道水莲移动的水平距离为2米 ,问这里水深多少?
实践应用
DA
C
B
D
B
A
例题:它高出水面1米? , 水莲被吹至一边,花朵齐及水面,如果知道水莲移动的水平距离为2米 ,问这里水深多少?
谈谈你的收获!
1.完成课本习题1、2、3(必做)
2.课后小实验:如图,分别以直角三角形的三 边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么? (必做)
3.做一棵奇妙的勾股树(选做)
作业快餐:
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3)????
