人教版八年级数学上册 12.2三角形全等的判定课件(第1课时 共17张PPT)
文档属性
| 名称 | 人教版八年级数学上册 12.2三角形全等的判定课件(第1课时 共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 381.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第十二章 全等三角形
学习新知
检测反馈
12.2 三角形全等的判定(1)
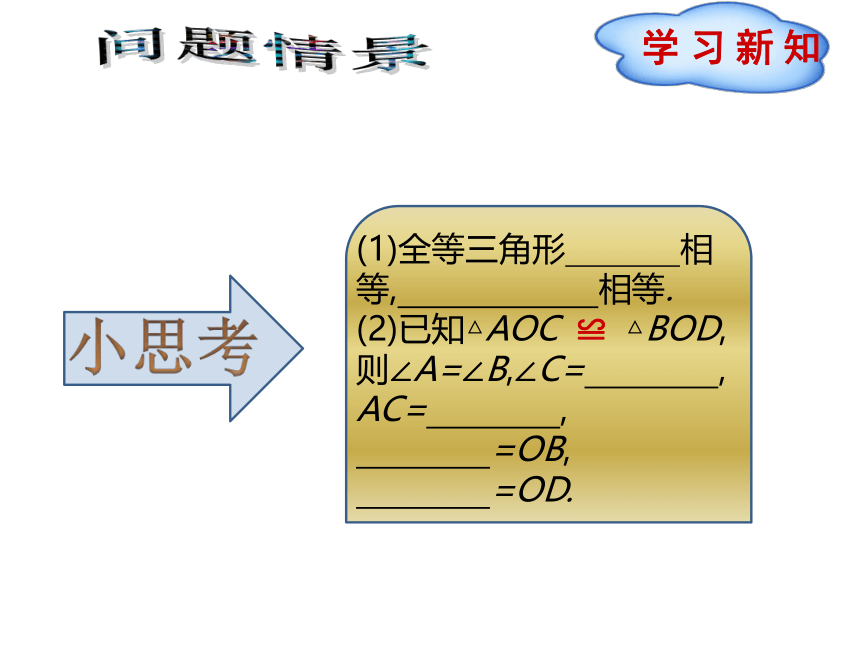
问题情景
小思考
(1)全等三角形 相等, 相等.?
(2)已知△AOC ≌ △BOD,则∠A=∠B,∠C= ,
AC= ,
=OB,
=OD.?
学 习 新 知
一、探究三角形全等的条件
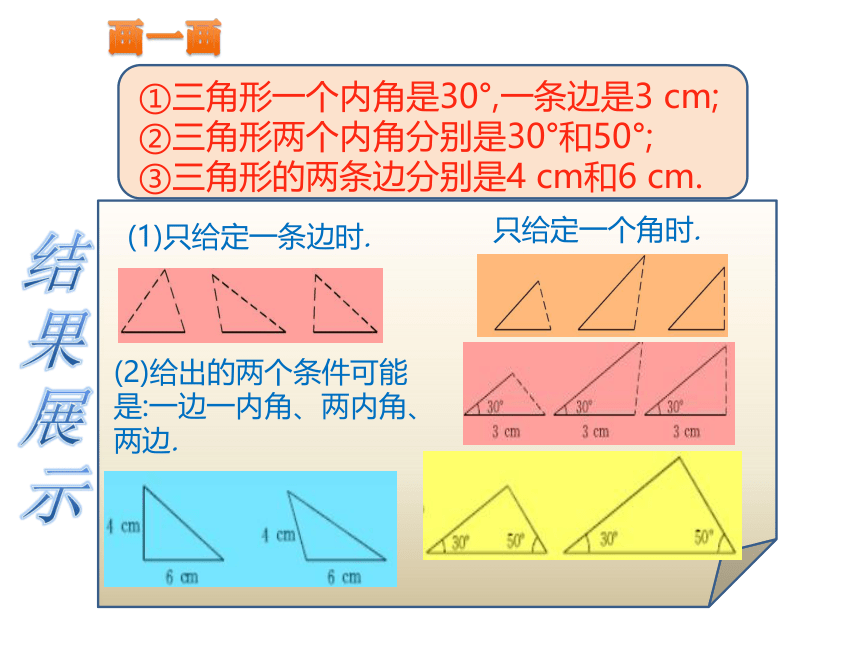
(1)只给一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
小讨论
(2)如果给出两个条件呢?给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?
①三角形一个内角是30°,一条边是3 cm;
②三角形两个内角分别是30°和50°;
③三角形的两条边分别是4 cm和6 cm.
画一画
结
果
展
示
(1)只给定一条边时.
只给定一个角时.
(2)给出的两个条件可能
是:一边一内角、两内角、
两边.
议一议
如果给出三个条件画三角形时,你能说出有几种情况吗?
三条边,两条边一个角,一条边两个角,三个角
用你们准备的4 cm,5 cm,7 cm长的三根细木棒拼一个三角形,与其他同学拼成的三角形比较,它们一定全等吗?你又发现了什么?
这些三角形都是全等的.
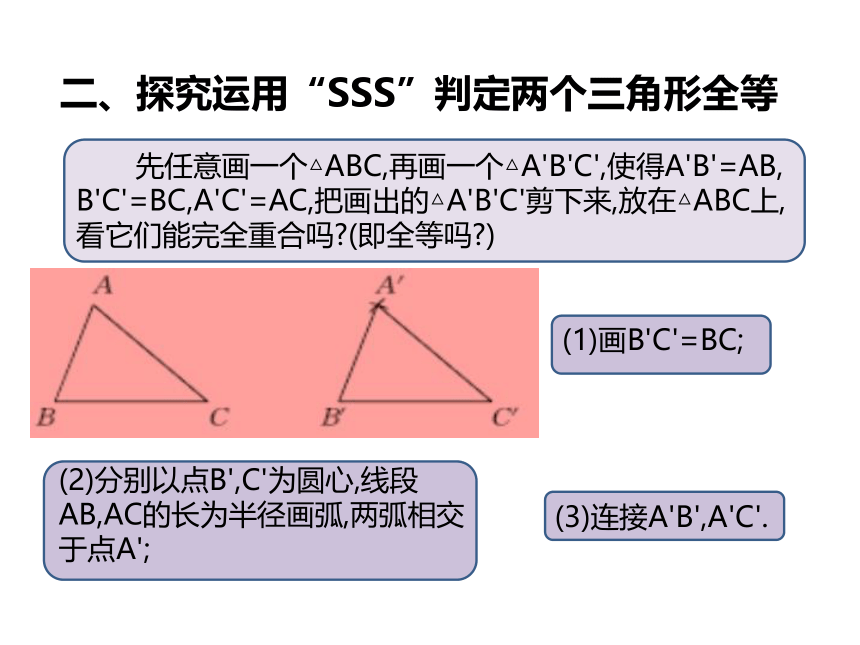
二、探究运用“SSS”判定两个三角形全等
先任意画一个△ABC,再画一个△A'B'C',使得A'B'=AB,
B'C'=BC,A'C'=AC,把画出的△A'B'C'剪下来,放在△ABC上,看它们能完全重合吗?(即全等吗?)
(1)画B'C'=BC;
(3)连接A'B',A'C'.
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
归纳总结定理
如果两个三角形的三边对应相等,那么这两个三角形全等.
证明:∵D是BC的中点,
解析:要证△ABD ≌ △ACD,只需说明这两个三角形的三条边对应相等.
∴BD=CD.
在△ABD和△ACD中,
∴△ABD ≌ △ACD(SSS).
题目中的隐含条件是AD是公共边.
证明三角形全等的书写格式可分为三部分:第一部分是全等条件的证明;第二部分是罗列两个三角形全等的条件;第三部分是下三角形全等的结论.这里要求注明判定方法.
注意
方法技巧
例1 在如图所示的三角形钢架中,
AB=AC,AD是连接点A与BC中点
D的支架.求证△ABD ≌ △ACD.
如图所示,已知:∠AOB,求作:∠A'O'B',使∠A'O'B'=∠AOB.
三、作一个角等于已知角
如图所示,(1)作射线O'A';
作一个角等于已知角的依据是什么?
讨论
作法
(3)以O‘ 为圆心,以OC的长为半径画弧,交O'A'于点C';
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D ;
(5)过D‘作射线O’B‘ ,则∠A'O'B'就是所求作的角.
(4)以点C‘ 为圆心,以CD的长为半径画弧,交前弧于点D';
如果两个三角形的三边对应相等,那么这两个三角形全等,称为“边边边”定理,利用两三角形全等可进行一些相关计算和证明.
知识小结
C
解析:AE为公共边,AB=AC,BE=CE,则△ABE ≌ △ACE(SSS).故选C.
1.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定 ( )
A.△ABD ≌ △ACD
B.△BDE ≌ △CDE
C.△ABE ≌ △ACE
D.以上都不对
检测反馈
EC
解析:∵BD=BC-CD,EC=DE-CD,
BC=DE,
∴在△ACE 与△FDB 中
∴△ACE ≌ △FDB (SSS).
△FDB
SSS
2.如图所示,点B,C,D,E在一条直线上,且BC=DE,
AC=FD,AE=FB,则BD= ,△ACE ≌ ,理由是 .
解析:添加AC=DF.
∵BE=CF,∴BE+EC=CF+EC
?BC=EF.
在△ABC和△DEF中,
∴△ABC ≌ △DEF(SSS).
故填AC=DF.
3.如图所示,点B,E,C,F在一条直线上,AB=DE,BE=CF,请添加一个条件: ,使△ABC ≌△DEF(SSS).
AC=DF
解析:连接AC,由于AB=AD,
CB=CD,AC=AC,利用“SSS”可证得△ABC ≌ △ADC,于是∠B=∠D.
证明:连接AC,在△ABC和△ADC中,∴△ABC ≌ △ADC(SSS),
∴∠B=∠D.
4.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.
必做题
教材第37页练习第1,2题.
选做题
教材第43页习题12.2第1题.
布置作业
第十二章 全等三角形
学习新知
检测反馈
12.2 三角形全等的判定(1)
问题情景
小思考
(1)全等三角形 相等, 相等.?
(2)已知△AOC ≌ △BOD,则∠A=∠B,∠C= ,
AC= ,
=OB,
=OD.?
学 习 新 知
一、探究三角形全等的条件
(1)只给一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
小讨论
(2)如果给出两个条件呢?给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?
①三角形一个内角是30°,一条边是3 cm;
②三角形两个内角分别是30°和50°;
③三角形的两条边分别是4 cm和6 cm.
画一画
结
果
展
示
(1)只给定一条边时.
只给定一个角时.
(2)给出的两个条件可能
是:一边一内角、两内角、
两边.
议一议
如果给出三个条件画三角形时,你能说出有几种情况吗?
三条边,两条边一个角,一条边两个角,三个角
用你们准备的4 cm,5 cm,7 cm长的三根细木棒拼一个三角形,与其他同学拼成的三角形比较,它们一定全等吗?你又发现了什么?
这些三角形都是全等的.
二、探究运用“SSS”判定两个三角形全等
先任意画一个△ABC,再画一个△A'B'C',使得A'B'=AB,
B'C'=BC,A'C'=AC,把画出的△A'B'C'剪下来,放在△ABC上,看它们能完全重合吗?(即全等吗?)
(1)画B'C'=BC;
(3)连接A'B',A'C'.
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
归纳总结定理
如果两个三角形的三边对应相等,那么这两个三角形全等.
证明:∵D是BC的中点,
解析:要证△ABD ≌ △ACD,只需说明这两个三角形的三条边对应相等.
∴BD=CD.
在△ABD和△ACD中,
∴△ABD ≌ △ACD(SSS).
题目中的隐含条件是AD是公共边.
证明三角形全等的书写格式可分为三部分:第一部分是全等条件的证明;第二部分是罗列两个三角形全等的条件;第三部分是下三角形全等的结论.这里要求注明判定方法.
注意
方法技巧
例1 在如图所示的三角形钢架中,
AB=AC,AD是连接点A与BC中点
D的支架.求证△ABD ≌ △ACD.
如图所示,已知:∠AOB,求作:∠A'O'B',使∠A'O'B'=∠AOB.
三、作一个角等于已知角
如图所示,(1)作射线O'A';
作一个角等于已知角的依据是什么?
讨论
作法
(3)以O‘ 为圆心,以OC的长为半径画弧,交O'A'于点C';
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D ;
(5)过D‘作射线O’B‘ ,则∠A'O'B'就是所求作的角.
(4)以点C‘ 为圆心,以CD的长为半径画弧,交前弧于点D';
如果两个三角形的三边对应相等,那么这两个三角形全等,称为“边边边”定理,利用两三角形全等可进行一些相关计算和证明.
知识小结
C
解析:AE为公共边,AB=AC,BE=CE,则△ABE ≌ △ACE(SSS).故选C.
1.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定 ( )
A.△ABD ≌ △ACD
B.△BDE ≌ △CDE
C.△ABE ≌ △ACE
D.以上都不对
检测反馈
EC
解析:∵BD=BC-CD,EC=DE-CD,
BC=DE,
∴在△ACE 与△FDB 中
∴△ACE ≌ △FDB (SSS).
△FDB
SSS
2.如图所示,点B,C,D,E在一条直线上,且BC=DE,
AC=FD,AE=FB,则BD= ,△ACE ≌ ,理由是 .
解析:添加AC=DF.
∵BE=CF,∴BE+EC=CF+EC
?BC=EF.
在△ABC和△DEF中,
∴△ABC ≌ △DEF(SSS).
故填AC=DF.
3.如图所示,点B,E,C,F在一条直线上,AB=DE,BE=CF,请添加一个条件: ,使△ABC ≌△DEF(SSS).
AC=DF
解析:连接AC,由于AB=AD,
CB=CD,AC=AC,利用“SSS”可证得△ABC ≌ △ADC,于是∠B=∠D.
证明:连接AC,在△ABC和△ADC中,∴△ABC ≌ △ADC(SSS),
∴∠B=∠D.
4.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.
必做题
教材第37页练习第1,2题.
选做题
教材第43页习题12.2第1题.
布置作业
