2019-2020学年度九年级下册数学4月份适应性测试卷(PDF版无答案)
文档属性
| 名称 | 2019-2020学年度九年级下册数学4月份适应性测试卷(PDF版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 617.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 00:00:00 | ||
图片预览

文档简介
1
初三数学自主适应性练习 4.20
班级 姓名___________
一、 选择题(本题共 16 分,每小题 2 分)
1、下列图形中,既是中心对称图形,也是轴对称图形的是( )
A.赵爽弦图 B.科克曲线 C.河图幻方 D.谢尔宾斯基三角形
2、若正多边形的一个外角是 72°,则该正多边形的边数是( )
A. 5 B. 6 C. 4 D.3
3、 如图, 点 A、B、C 在⊙O上, 若?C=40?, 则?AOB 的度数为( )
A.20? B.40? C.80? D.100?
4、袋子中有 42 个除颜色外完全相同的小球. 在看不到球的条件下,随机地从袋子中摸出
一个球,记录颜色后放回,将球摇匀. 重复上述过程 180 次后,共摸到红球 30 次,由此可以
估计口袋中的红球个数是( )
A.6 B. 9 C.8 D.7
5、如图,在△ABC 中,?C=90?, 点 D 在 CB 上,DE⊥AB 于 E,若 DE=2, CA=4,则
DB
AB
的
值为( )
A.
4
1
B.
1
2
C.
3
1
D.
3
2
6、下列图形中,能通过折叠围成一个三棱柱的是( )
A B C D
7、“北京市慈善义工协会” 于 2012 年 3 月开展了“学雷锋 新雷锋”公益月活动, 主题是“弘
扬雷锋精神,慈善义工与你同行”. 某校初三年级参加了“维护小区周边环境、维护繁华街
道卫生、义务指路”等慈善活动, 右图是根据该校初三年级六个班的同学某天“义务指
路”总人次所绘制的折线统计图,则下列说法正确的是( )
A. 众数是 58 B. 平均数是 60 C. 中位数是 51.5 D. 极差是 40
E
D
C
BA
C
B A
O
初三年级六个班级的同学“义务指路”
总人次折线统计图
58
62
80
45
58
50
6班5班4班3班2班1班
80
70
60
50
40
30
20
10
0
总人次
班级
初三年级六个班的同学某天“义务指路”
总人次折线统计图
2
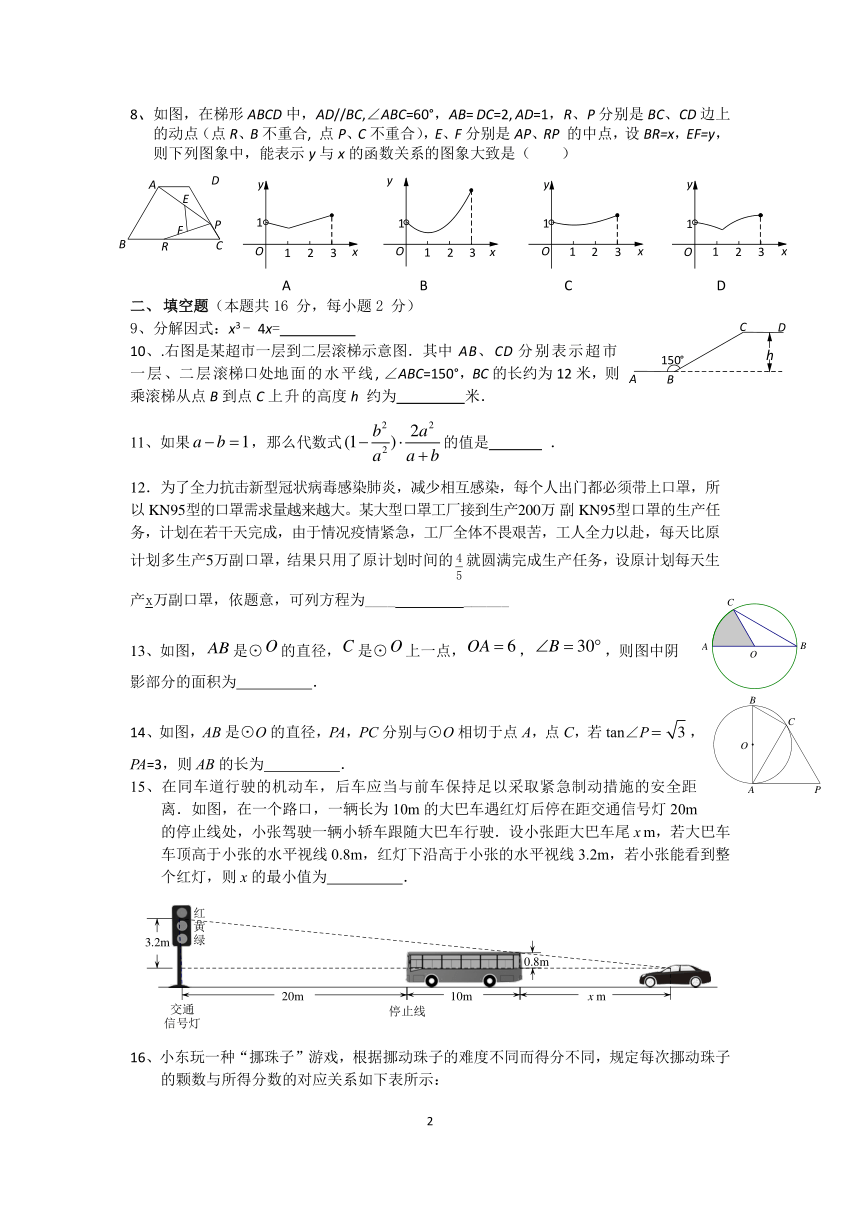
8、如图,在梯形 ABCD 中,AD//BC,∠ABC=60°,AB= DC=2, AD=1,R、P 分别是 BC、CD 边上
的动点(点 R、B 不重合, 点 P、C 不重合),E、F 分别是 AP、RP 的中点,设 BR=x,EF=y,
则下列图象中,能表示 y 与 x 的函数关系的图象大致是( )
A B C D
二、 填空题(本题共 16 分,每小题 2 分)
9、分解因式:x3 - 4x=
10、.右图是某超市一层到二层滚梯示意图.其中 AB、CD 分别表示超市
一层、二层滚梯口处地面的水平线 , ∠ABC=150°,BC 的长约为 12 米,则
乘滚梯从点 B 到点 C 上升的高度 h 约为 米.
11、如果 1a b? = ,那么代数式
2 2
2
2
(1 )
b a
a a b
? ?
+
的值是 .
12.为了全力抗击新型冠状病毒感染肺炎,减少相互感染,每个人出门都必须带上口罩,所
以 KN95型的口罩需求量越来越大。某大型口罩工厂接到生产200万副 KN95型口罩的生产任
务,计划在若干天完成,由于情况疫情紧急,工厂全体不畏艰苦,工人全力以赴,每天比原
计划多生产5万副口罩,结果只用了原计划时间的
5
4 就圆满完成生产任务,设原计划每天生
产x万副口罩,依题意,可列方程为____ ______
13、如图,AB 是⊙O的直径,C 是⊙O上一点, 6OA = , 30B? = ?,则图中阴
影部分的面积为 .
14、如图,AB 是⊙O 的直径,PA,PC 分别与⊙O 相切于点 A,点 C,若 tan∠P= 3 ,
PA=3,则 AB 的长为 .
15、在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距
离.如图,在一个路口,一辆长为 10m 的大巴车遇红灯后停在距交通信号灯 20m
的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾 x m,若大巴车
车顶高于小张的水平视线 0.8m,红灯下沿高于小张的水平视线 3.2m,若小张能看到整
个红灯,则 x 的最小值为 .
16、小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子
的颗数与所得分数的对应关系如下表所示:
绿
黄
红
停止线 交通
信号灯
0.8m
x m
3.2m
10m20m
150 °
A B
C D
h
y
x O O x
y
1 2 3
1
O x
y
1 2 3
1
1 2 3
1 1
3 2 1
y
x O
F
E
R
P
B C
D A
O
C
BA
O
C
B
A P
3
挪动珠子数(颗) 2 3 4 5 6 …
所得分数(分) 5 11 19 29 41 …
按表中规律,当所得分数为 71 分时,则挪动的珠子数为 颗; 当挪动 n 颗
珠子时(n 为大于 1 的整数), 所得分数为 (用含 n 的代数式表示).
三、解答题(17—22题,每题 5分,23--24题各 6 分,25题 5分,26—27题各 7分)
17、计算: 10 )
3
1
(45sin28π)14.3( ?+??+?
18、解不等式组:
( )5 3 3 1 ,
2
6 3 .
2
x x
x
x
+ ? ??
?
? ?
? ??
?
19.如图,在△ABC 中,∠B 为锐角, AB= 3 2 ,AC= 5, sin
3
5
C = ,求 BC 的长.
20、反比例 21.如图,在平面直角坐标系 xOy 中,函数 ( )0
k
y x
x
= ?
的图象经过点 ,作 AC⊥x 轴于点 C.
(1)求 k 的值;
(2)直线 AB: ( )0y ax b a= + ? 图象经过点 交 x 轴于点 .横、
纵坐标都是整数的点叫做整点.线段 AB,AC,BC 围成的区域(不
含边界)为 W.
①直线 AB 经过 ( )0,1 时,直接写出区域 W 内的整点个数;
②若区域 W 内恰有 1 个整点,结合函数图象,求 a 的取值范围.
21、评价组对某区九年级教师的试卷讲评课的学生参与度进行评价调查,其评价项目为主
动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名同学的参与
情况,绘制成如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息
解答下列问题:
(1)在这次评价中,一共抽查了 名同学;
(2)请将条形统计图补充完整;
(3)如果全区有 6 000 名九年级学生,那么在试卷评讲课中“独立思考”的约有多少人?
(4)根据统计反映的情况,请你对该区的九年级同学提出一条对待试卷讲评课的建议.
22、如图,在△ABC 中,∠ACB=90°,D 是 BC 边上的一点,分别过点 A、B 作
BD、AD 的平行线交于点 E,且 AB 平分∠EAD.
(1)求证:四边形 EADB 是菱形;
(2)连接 EC,当∠BAC=60°,BC= 2 3 时,求△ECB 的面积.
E
D
A C
B
CB
A
4
E F CB
O
A D
23、已知关于 x 的一元二次方程方程 03)13(2 =+++ xmmx .
(1)求证: 不论 m 为任何实数, 此方程总有实数根;
(2)若抛物线 ( )2 3 1 3y mx m x= + + + 与 x 轴交于两个不同的整数点,且m 为正整数,试
确定此抛物线的解析式;
(3)若点 P ),( 11 yx 与 Q ),( 21 ynx + 在(2)中抛物线上 (点 P、Q 不重合), 且 y1=y2,
求代数式 8165124 21
2
1 ++++ nnnxx 的值.
24、如图,△ABC 内接于⊙O, AD 是⊙O 直径, E 是 CB 延长线上一点, 且?BAE=?C.
(1)求证:直线 AE 是⊙O 的切线;
(2)若 EB=AB ,
5
4
cos =E , AE=24,求 EB 的长及⊙O 的半径.
25. 如图,正方形 ABCD 的对角线相交于点 O,点 E,F 分别是边 BC 上两点,且
45EOF? = ?.将 EOF? 绕点 O 逆时针旋转,当点 F 与点 C 重合时,停止旋转.
已知,BC=6,设 BE=x,EF=y.
小明根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量 x 的值进行取点、画图、测量,得到了 y 与 x 的几组对应值;
x 0 0.5 1 1.5 2 2.5 3
y 3 2.77 2.50 2.55 2.65
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数
的图象;
(3)结合函数图象,解决问题:当 EF=2BE 时,BE 的长度约为 .
5
26. 在平面直角坐标系 xOy 中,抛物线 12
2
1 2 +?+= axaxy 与 y 轴交于点 C,
与 x 轴交于 A,B 两点(点 A 在点 B 左侧),且点 A 的横坐标为﹣1.
(1)求 a 的值;
(2)设抛物线的顶点 P 关于原点的对称点为 P′,求点 P′的坐标;
(3)将抛物线在 A,B 两点之间的部分(包括 A,B 两点),先向下平移 3 个
单位,再向左平移 m( 0?m )个单位,平移后的图象记为图象 G,
若图象 G 与直线 PP′ 无交点,求 m 的取值范围.
27、已知在Rt BAC△ 中, 90BAC? = °, AB AC= ,点 D 为射线 BC 上一点(与点 B 不重
合),过点C 作CE ⊥ BC 于点C ,且CE BD= (点 E 与点 A在射线 BC 同侧),连接 AD ,
ED .
(1)如图1,当点 D在线段 BC 上时,请直接写出 ADE? 的度数.
(2)当点 D在线段 BC 的延长线上时,依题意在图 2中补全图形并判断(1)中结论是否
成立?若成立,请证明;若不成立,请说明理由.
(3)在(1)的条件下, ED 与 AC 相交于点 P ,若 2AB = ,直接写出CP 的最大值.
28、如图,在平面直角坐标系 xOy 中,点 A 与点 B 的坐标分别是(1,0),(7,0).
(1)对于坐标平面内的一点 P,给出如下定义:如果∠APB=45°,则称点 P 为线段 AB
的“等角点”. 显然,线段 AB 的“等角点”有无数个,且 A、B、P 三点共圆.
① 设 A、B、P 三点所在圆的圆心为 C,直接写出点 C 的坐标和⊙C 的半径;
②y 轴正半轴上是否有线段 AB 的“等角点”?如果有,求出“等角点”的坐标;如
果没有,请说明理由;
(2)当点 P 在 y 轴正半轴上运动时,∠APB 是否有最大值?如果有,说明此时∠APB
最大的理由,并求出点 P 的坐标;如果没有,也请说明理由.
O
y
x-1
-2
-4
-3
-6
-5
-1-2-4-6 -5 -3
1
2
4
3
6
5
1 2 43 65
图 1 图 2 备用图
E
A
B CD
A
B C D
P
E
A
B CD
x
y
45°
P
BA
1
2
3
4
5
6
7
1 2 3 4 5 6 7 8 9–1–2
–1
–2
–3
–4
–5
O
初三数学自主适应性练习 4.20
班级 姓名___________
一、 选择题(本题共 16 分,每小题 2 分)
1、下列图形中,既是中心对称图形,也是轴对称图形的是( )
A.赵爽弦图 B.科克曲线 C.河图幻方 D.谢尔宾斯基三角形
2、若正多边形的一个外角是 72°,则该正多边形的边数是( )
A. 5 B. 6 C. 4 D.3
3、 如图, 点 A、B、C 在⊙O上, 若?C=40?, 则?AOB 的度数为( )
A.20? B.40? C.80? D.100?
4、袋子中有 42 个除颜色外完全相同的小球. 在看不到球的条件下,随机地从袋子中摸出
一个球,记录颜色后放回,将球摇匀. 重复上述过程 180 次后,共摸到红球 30 次,由此可以
估计口袋中的红球个数是( )
A.6 B. 9 C.8 D.7
5、如图,在△ABC 中,?C=90?, 点 D 在 CB 上,DE⊥AB 于 E,若 DE=2, CA=4,则
DB
AB
的
值为( )
A.
4
1
B.
1
2
C.
3
1
D.
3
2
6、下列图形中,能通过折叠围成一个三棱柱的是( )
A B C D
7、“北京市慈善义工协会” 于 2012 年 3 月开展了“学雷锋 新雷锋”公益月活动, 主题是“弘
扬雷锋精神,慈善义工与你同行”. 某校初三年级参加了“维护小区周边环境、维护繁华街
道卫生、义务指路”等慈善活动, 右图是根据该校初三年级六个班的同学某天“义务指
路”总人次所绘制的折线统计图,则下列说法正确的是( )
A. 众数是 58 B. 平均数是 60 C. 中位数是 51.5 D. 极差是 40
E
D
C
BA
C
B A
O
初三年级六个班级的同学“义务指路”
总人次折线统计图
58
62
80
45
58
50
6班5班4班3班2班1班
80
70
60
50
40
30
20
10
0
总人次
班级
初三年级六个班的同学某天“义务指路”
总人次折线统计图
2
8、如图,在梯形 ABCD 中,AD//BC,∠ABC=60°,AB= DC=2, AD=1,R、P 分别是 BC、CD 边上
的动点(点 R、B 不重合, 点 P、C 不重合),E、F 分别是 AP、RP 的中点,设 BR=x,EF=y,
则下列图象中,能表示 y 与 x 的函数关系的图象大致是( )
A B C D
二、 填空题(本题共 16 分,每小题 2 分)
9、分解因式:x3 - 4x=
10、.右图是某超市一层到二层滚梯示意图.其中 AB、CD 分别表示超市
一层、二层滚梯口处地面的水平线 , ∠ABC=150°,BC 的长约为 12 米,则
乘滚梯从点 B 到点 C 上升的高度 h 约为 米.
11、如果 1a b? = ,那么代数式
2 2
2
2
(1 )
b a
a a b
? ?
+
的值是 .
12.为了全力抗击新型冠状病毒感染肺炎,减少相互感染,每个人出门都必须带上口罩,所
以 KN95型的口罩需求量越来越大。某大型口罩工厂接到生产200万副 KN95型口罩的生产任
务,计划在若干天完成,由于情况疫情紧急,工厂全体不畏艰苦,工人全力以赴,每天比原
计划多生产5万副口罩,结果只用了原计划时间的
5
4 就圆满完成生产任务,设原计划每天生
产x万副口罩,依题意,可列方程为____ ______
13、如图,AB 是⊙O的直径,C 是⊙O上一点, 6OA = , 30B? = ?,则图中阴
影部分的面积为 .
14、如图,AB 是⊙O 的直径,PA,PC 分别与⊙O 相切于点 A,点 C,若 tan∠P= 3 ,
PA=3,则 AB 的长为 .
15、在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距
离.如图,在一个路口,一辆长为 10m 的大巴车遇红灯后停在距交通信号灯 20m
的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾 x m,若大巴车
车顶高于小张的水平视线 0.8m,红灯下沿高于小张的水平视线 3.2m,若小张能看到整
个红灯,则 x 的最小值为 .
16、小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子
的颗数与所得分数的对应关系如下表所示:
绿
黄
红
停止线 交通
信号灯
0.8m
x m
3.2m
10m20m
150 °
A B
C D
h
y
x O O x
y
1 2 3
1
O x
y
1 2 3
1
1 2 3
1 1
3 2 1
y
x O
F
E
R
P
B C
D A
O
C
BA
O
C
B
A P
3
挪动珠子数(颗) 2 3 4 5 6 …
所得分数(分) 5 11 19 29 41 …
按表中规律,当所得分数为 71 分时,则挪动的珠子数为 颗; 当挪动 n 颗
珠子时(n 为大于 1 的整数), 所得分数为 (用含 n 的代数式表示).
三、解答题(17—22题,每题 5分,23--24题各 6 分,25题 5分,26—27题各 7分)
17、计算: 10 )
3
1
(45sin28π)14.3( ?+??+?
18、解不等式组:
( )5 3 3 1 ,
2
6 3 .
2
x x
x
x
+ ? ??
?
? ?
? ??
?
19.如图,在△ABC 中,∠B 为锐角, AB= 3 2 ,AC= 5, sin
3
5
C = ,求 BC 的长.
20、反比例 21.如图,在平面直角坐标系 xOy 中,函数 ( )0
k
y x
x
= ?
的图象经过点 ,作 AC⊥x 轴于点 C.
(1)求 k 的值;
(2)直线 AB: ( )0y ax b a= + ? 图象经过点 交 x 轴于点 .横、
纵坐标都是整数的点叫做整点.线段 AB,AC,BC 围成的区域(不
含边界)为 W.
①直线 AB 经过 ( )0,1 时,直接写出区域 W 内的整点个数;
②若区域 W 内恰有 1 个整点,结合函数图象,求 a 的取值范围.
21、评价组对某区九年级教师的试卷讲评课的学生参与度进行评价调查,其评价项目为主
动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名同学的参与
情况,绘制成如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息
解答下列问题:
(1)在这次评价中,一共抽查了 名同学;
(2)请将条形统计图补充完整;
(3)如果全区有 6 000 名九年级学生,那么在试卷评讲课中“独立思考”的约有多少人?
(4)根据统计反映的情况,请你对该区的九年级同学提出一条对待试卷讲评课的建议.
22、如图,在△ABC 中,∠ACB=90°,D 是 BC 边上的一点,分别过点 A、B 作
BD、AD 的平行线交于点 E,且 AB 平分∠EAD.
(1)求证:四边形 EADB 是菱形;
(2)连接 EC,当∠BAC=60°,BC= 2 3 时,求△ECB 的面积.
E
D
A C
B
CB
A
4
E F CB
O
A D
23、已知关于 x 的一元二次方程方程 03)13(2 =+++ xmmx .
(1)求证: 不论 m 为任何实数, 此方程总有实数根;
(2)若抛物线 ( )2 3 1 3y mx m x= + + + 与 x 轴交于两个不同的整数点,且m 为正整数,试
确定此抛物线的解析式;
(3)若点 P ),( 11 yx 与 Q ),( 21 ynx + 在(2)中抛物线上 (点 P、Q 不重合), 且 y1=y2,
求代数式 8165124 21
2
1 ++++ nnnxx 的值.
24、如图,△ABC 内接于⊙O, AD 是⊙O 直径, E 是 CB 延长线上一点, 且?BAE=?C.
(1)求证:直线 AE 是⊙O 的切线;
(2)若 EB=AB ,
5
4
cos =E , AE=24,求 EB 的长及⊙O 的半径.
25. 如图,正方形 ABCD 的对角线相交于点 O,点 E,F 分别是边 BC 上两点,且
45EOF? = ?.将 EOF? 绕点 O 逆时针旋转,当点 F 与点 C 重合时,停止旋转.
已知,BC=6,设 BE=x,EF=y.
小明根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量 x 的值进行取点、画图、测量,得到了 y 与 x 的几组对应值;
x 0 0.5 1 1.5 2 2.5 3
y 3 2.77 2.50 2.55 2.65
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数
的图象;
(3)结合函数图象,解决问题:当 EF=2BE 时,BE 的长度约为 .
5
26. 在平面直角坐标系 xOy 中,抛物线 12
2
1 2 +?+= axaxy 与 y 轴交于点 C,
与 x 轴交于 A,B 两点(点 A 在点 B 左侧),且点 A 的横坐标为﹣1.
(1)求 a 的值;
(2)设抛物线的顶点 P 关于原点的对称点为 P′,求点 P′的坐标;
(3)将抛物线在 A,B 两点之间的部分(包括 A,B 两点),先向下平移 3 个
单位,再向左平移 m( 0?m )个单位,平移后的图象记为图象 G,
若图象 G 与直线 PP′ 无交点,求 m 的取值范围.
27、已知在Rt BAC△ 中, 90BAC? = °, AB AC= ,点 D 为射线 BC 上一点(与点 B 不重
合),过点C 作CE ⊥ BC 于点C ,且CE BD= (点 E 与点 A在射线 BC 同侧),连接 AD ,
ED .
(1)如图1,当点 D在线段 BC 上时,请直接写出 ADE? 的度数.
(2)当点 D在线段 BC 的延长线上时,依题意在图 2中补全图形并判断(1)中结论是否
成立?若成立,请证明;若不成立,请说明理由.
(3)在(1)的条件下, ED 与 AC 相交于点 P ,若 2AB = ,直接写出CP 的最大值.
28、如图,在平面直角坐标系 xOy 中,点 A 与点 B 的坐标分别是(1,0),(7,0).
(1)对于坐标平面内的一点 P,给出如下定义:如果∠APB=45°,则称点 P 为线段 AB
的“等角点”. 显然,线段 AB 的“等角点”有无数个,且 A、B、P 三点共圆.
① 设 A、B、P 三点所在圆的圆心为 C,直接写出点 C 的坐标和⊙C 的半径;
②y 轴正半轴上是否有线段 AB 的“等角点”?如果有,求出“等角点”的坐标;如
果没有,请说明理由;
(2)当点 P 在 y 轴正半轴上运动时,∠APB 是否有最大值?如果有,说明此时∠APB
最大的理由,并求出点 P 的坐标;如果没有,也请说明理由.
O
y
x-1
-2
-4
-3
-6
-5
-1-2-4-6 -5 -3
1
2
4
3
6
5
1 2 43 65
图 1 图 2 备用图
E
A
B CD
A
B C D
P
E
A
B CD
x
y
45°
P
BA
1
2
3
4
5
6
7
1 2 3 4 5 6 7 8 9–1–2
–1
–2
–3
–4
–5
O
同课章节目录
