湖南省茶陵县第三中学2019-2020学年高一下学期入学考试数学试题 Word版含答案
文档属性
| 名称 | 湖南省茶陵县第三中学2019-2020学年高一下学期入学考试数学试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-25 00:00:00 | ||
图片预览


文档简介
2020年上期茶陵三中入学考试
数学
考试范围:必修一、二、四;考试时间:120分钟
选择题(每小题5分,共60分)
1、设集合,,则
A.??????????B.??????????C.??????????D.??????????
2、的值是( )
A.??????????B.??????????C. ??????????D.??????????
3、角的终边经过点,那么的值为(???)
A.??????????B.??????????C.??????????D.??????????
4、一个几何体的三视图如图所示,则这个几何体的体积是(???) A.72??????????B.48??????????C.27??????????D.36??????????
5、已知且,则的终边在( ??)
A.第一象限??????????B.第二象限??????????C.第三象限??????????D.第四象限??????????
6、函数的最小正周期为(??)
A.??????????B.??????????C.??????????D.??????????
7、已知点A(1,-2)、B(m,2),且线段AB的垂直平分线是x+2y-2=0,则m为 ( )
A.-2??????????B.3??????????C.-7??????????D.1??????????
8、要得到函数的图象,只需将函数的图象(???)
A.向右平移个单位长度??????????????????????????????B.向左平移个单位长度 C.向右平移个单位长度??????????????????????????????D.向左平移个单位长度
9、已知向量,,若,则(???)
A.??????????B.??????????C.2??????????D.4??????????
10、函数f(x)=ex+x﹣4的零点所在的区间为( )
A.(﹣1,0)??????????B.(1,2)??????????C.(0,1)??????????D.(2,3)??????
11、函数的最小正周期和振幅分别是(???)
A.,1??????????B.,2??????????C.,1??????????D.,2??????????
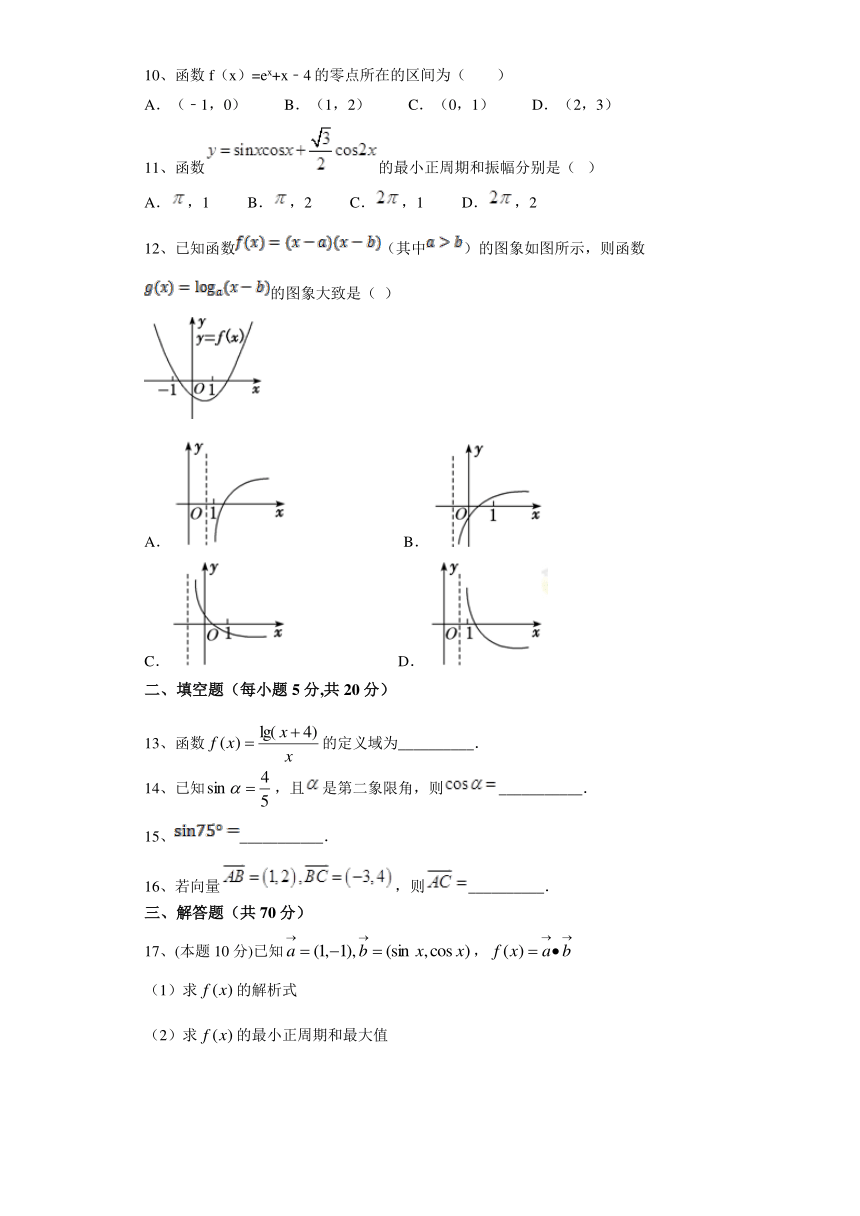
12、已知函数(其中)的图象如图所示,则函数的图象大致是(??)
A.??????????????????????????????B. C.??????????????????????????????D.
填空题(每小题5分,共20分)
13、函数的定义域为__________.
14、已知,且是第二象限角,则___________.
15、___________.
16、若向量,则__________.
三、解答题(共70分)
17、(本题10分)已知,
(1)求的解析式 (2)求的最小正周期和最大值
18、(本题12分)如图,ABCD是正方形,O是正方形ABCD的中心,,E是PC的中点 求证:(1)平面; (2)平面.
19、(本题12分)已知 (1)化简; (2)若,且是第二象限角,求的值.
20、(本题12分)已知曲线y=Asin(ùx+?)(A>0,ù>0)上的一个最高点的坐标为,由此点到相邻最低点间的曲线与x轴交于点, (1)求这条曲线的函数解析式; (2)写出函数的单调区间.
21、(本题12分)已知圆的圆心坐标,直线:被圆截得弦长为。 (Ⅰ)求圆的方程; (Ⅱ)从圆外一点向圆引切线,求切线方程。
22、(本题12分)已知定义在上的偶函数满足:当时,. (1)求函数在上的解析式; (2)设,若对于任意,都有成立,求实数的取值范围.
参考答案
一、选择题
1、B
2、A
3、C
4、D
5、C
6、C
7、B
8、B
9、C
10、B
11、A
12、B
二、填空题
13、 14、
15、 16、
三、解答题
17、解:(1)
由(1)可得,
解:(1) 连接,在中,, 又平面平面,平面
(2)底面平面,又四边形是正方形,平面平面. 19、(1)? (2) 又∵为第二象限角,∴,?????? , ∴?
20、解:(1)由题意可得A=,?=﹣,求得ù=. 再根据最高点的坐标为(,),可得sin(×+?)=,即sin(×+?)="1" ①. 再根据由此最高点到相邻最低点间的曲线与x轴交于点(e,0),可得得sin(×+?)=0,即sin(+?)="0" ②, 由①②求得?=,故曲线的解析式为y=sin(x+). (2)对于函数y=sin(x+),令2ke﹣≤+≤2ke+,求得4ke﹣≤x≤4ke+, 可得函数的增区间为[4ke﹣,4ke+],k∈Z. 令2ke+≤+≤2ke+,求得4ke+≤x≤4ke+, 可得函数的减区间为[4ke+,4ke+],k∈Z.
21、解析:(Ⅰ)设圆的标准方程为:? 圆心到直线的距离:, 则 圆的标准方程: (Ⅱ)①当切线斜率不存在时,设切线:,此时满足直线与圆相切。 ②当切线斜率存在时,设切线:,即 则圆心到直线的距离:? 解得:,即 则切线方程为: 综上,切线方程为:和
22、试题解析:(1)设,则,因为定义在偶函数, 所以,因为,所以 所以????????????????????? 4分 (2)因为对任意,都有成立,所以????? 5分 又因为是定义在上的偶函数,所以在区间和区间上的值域相同。 当时,设,则, 函数化为,则?????????? 8分? 又??????????????????????????????????10分 所以,所以,故a的取值范围为 ?????12分
数学
考试范围:必修一、二、四;考试时间:120分钟
选择题(每小题5分,共60分)
1、设集合,,则
A.??????????B.??????????C.??????????D.??????????
2、的值是( )
A.??????????B.??????????C. ??????????D.??????????
3、角的终边经过点,那么的值为(???)
A.??????????B.??????????C.??????????D.??????????
4、一个几何体的三视图如图所示,则这个几何体的体积是(???) A.72??????????B.48??????????C.27??????????D.36??????????
5、已知且,则的终边在( ??)
A.第一象限??????????B.第二象限??????????C.第三象限??????????D.第四象限??????????
6、函数的最小正周期为(??)
A.??????????B.??????????C.??????????D.??????????
7、已知点A(1,-2)、B(m,2),且线段AB的垂直平分线是x+2y-2=0,则m为 ( )
A.-2??????????B.3??????????C.-7??????????D.1??????????
8、要得到函数的图象,只需将函数的图象(???)
A.向右平移个单位长度??????????????????????????????B.向左平移个单位长度 C.向右平移个单位长度??????????????????????????????D.向左平移个单位长度
9、已知向量,,若,则(???)
A.??????????B.??????????C.2??????????D.4??????????
10、函数f(x)=ex+x﹣4的零点所在的区间为( )
A.(﹣1,0)??????????B.(1,2)??????????C.(0,1)??????????D.(2,3)??????
11、函数的最小正周期和振幅分别是(???)
A.,1??????????B.,2??????????C.,1??????????D.,2??????????
12、已知函数(其中)的图象如图所示,则函数的图象大致是(??)
A.??????????????????????????????B. C.??????????????????????????????D.
填空题(每小题5分,共20分)
13、函数的定义域为__________.
14、已知,且是第二象限角,则___________.
15、___________.
16、若向量,则__________.
三、解答题(共70分)
17、(本题10分)已知,
(1)求的解析式 (2)求的最小正周期和最大值
18、(本题12分)如图,ABCD是正方形,O是正方形ABCD的中心,,E是PC的中点 求证:(1)平面; (2)平面.
19、(本题12分)已知 (1)化简; (2)若,且是第二象限角,求的值.
20、(本题12分)已知曲线y=Asin(ùx+?)(A>0,ù>0)上的一个最高点的坐标为,由此点到相邻最低点间的曲线与x轴交于点, (1)求这条曲线的函数解析式; (2)写出函数的单调区间.
21、(本题12分)已知圆的圆心坐标,直线:被圆截得弦长为。 (Ⅰ)求圆的方程; (Ⅱ)从圆外一点向圆引切线,求切线方程。
22、(本题12分)已知定义在上的偶函数满足:当时,. (1)求函数在上的解析式; (2)设,若对于任意,都有成立,求实数的取值范围.
参考答案
一、选择题
1、B
2、A
3、C
4、D
5、C
6、C
7、B
8、B
9、C
10、B
11、A
12、B
二、填空题
13、 14、
15、 16、
三、解答题
17、解:(1)
由(1)可得,
解:(1) 连接,在中,, 又平面平面,平面
(2)底面平面,又四边形是正方形,平面平面. 19、(1)? (2) 又∵为第二象限角,∴,?????? , ∴?
20、解:(1)由题意可得A=,?=﹣,求得ù=. 再根据最高点的坐标为(,),可得sin(×+?)=,即sin(×+?)="1" ①. 再根据由此最高点到相邻最低点间的曲线与x轴交于点(e,0),可得得sin(×+?)=0,即sin(+?)="0" ②, 由①②求得?=,故曲线的解析式为y=sin(x+). (2)对于函数y=sin(x+),令2ke﹣≤+≤2ke+,求得4ke﹣≤x≤4ke+, 可得函数的增区间为[4ke﹣,4ke+],k∈Z. 令2ke+≤+≤2ke+,求得4ke+≤x≤4ke+, 可得函数的减区间为[4ke+,4ke+],k∈Z.
21、解析:(Ⅰ)设圆的标准方程为:? 圆心到直线的距离:, 则 圆的标准方程: (Ⅱ)①当切线斜率不存在时,设切线:,此时满足直线与圆相切。 ②当切线斜率存在时,设切线:,即 则圆心到直线的距离:? 解得:,即 则切线方程为: 综上,切线方程为:和
22、试题解析:(1)设,则,因为定义在偶函数, 所以,因为,所以 所以????????????????????? 4分 (2)因为对任意,都有成立,所以????? 5分 又因为是定义在上的偶函数,所以在区间和区间上的值域相同。 当时,设,则, 函数化为,则?????????? 8分? 又??????????????????????????????????10分 所以,所以,故a的取值范围为 ?????12分
同课章节目录
