沪科版数学八年级下册第十八章 勾股定理 检测卷(含答案)
文档属性
| 名称 | 沪科版数学八年级下册第十八章 勾股定理 检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 103.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 20:41:30 | ||
图片预览




文档简介
沪科版数学八年级下册第十八章检测卷
时间:120分钟 满分:150分
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.设直角三角形的两条直角边的长分别为a和b,斜边长为c,已知b=12,c=13,则a的值为( )
A.1 B.5 C.10 D.25
2.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
A.1,, B.6,8,10
C.5,12,13 D.,2,
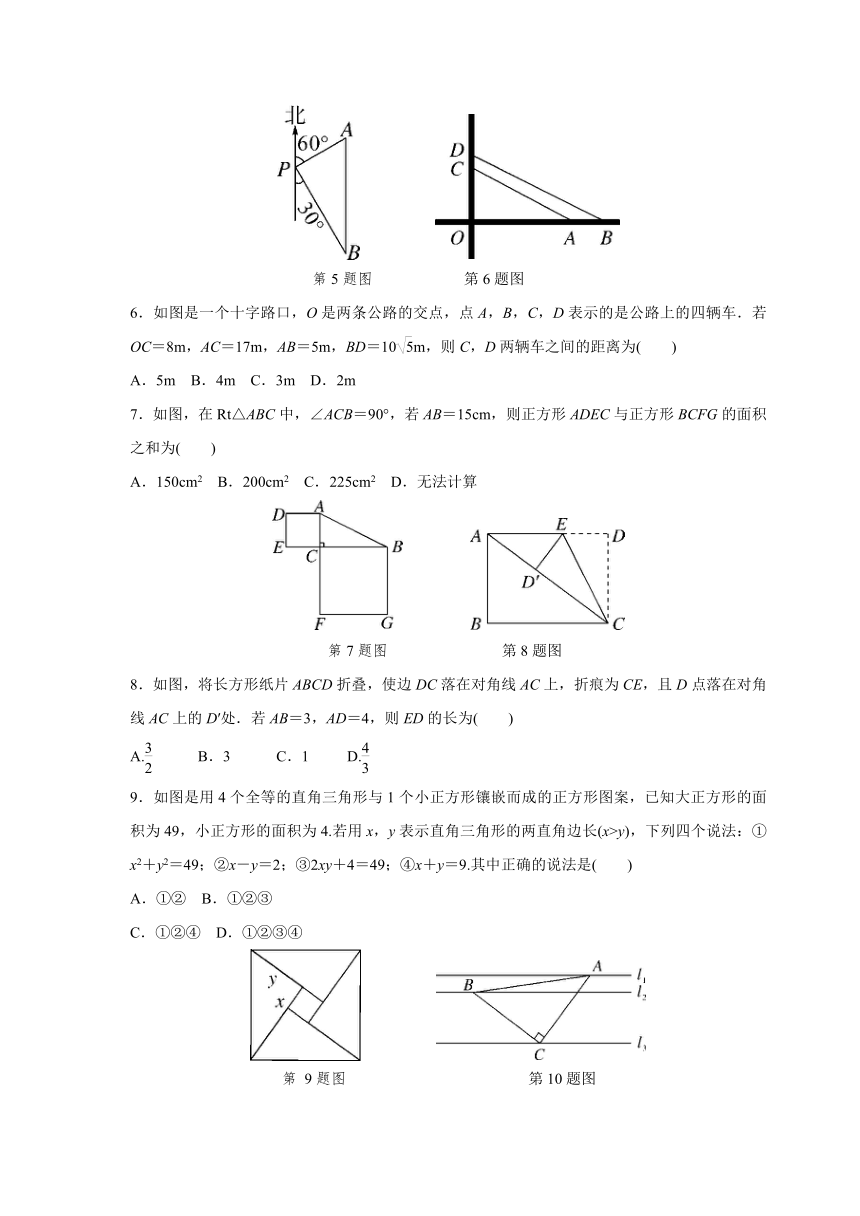
3.如图,点P是平面坐标系内一点,则点P到原点的距离是( )
A.3 B. C. D.
第3题图 第4题图
4.如图,已知AB⊥CD,△ABD,△BCE都是等腰直角三角形.如果CD=7,BE=3,那么AC的长为( )
A.8 B.5 C.3 D.4
5.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
A.60海里 B.45海里
C.20海里 D.30海里
第5题图 第6题图
6.如图是一个十字路口,O是两条公路的交点,点A,B,C,D表示的是公路上的四辆车.若OC=8m,AC=17m,AB=5m,BD=10m,则C,D两辆车之间的距离为( )
A.5m B.4m C.3m D.2m
7.如图,在Rt△ABC中,∠ACB=90°,若AB=15cm,则正方形ADEC与正方形BCFG的面积之和为( )
A.150cm2 B.200cm2 C.225cm2 D.无法计算
第7题图 第8题图
8.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线AC上的D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4.若用x,y表示直角三角形的两直角边长(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9.其中正确的说法是( )
A.①② B.①②③
C.①②④ D.①②③④
第 9题图 第10题图
10.如图,已知等腰直角三角形ABC的各顶点分别在直线l1,l2,l3上,且l1∥l2∥l3,l1,l2间的距离为1,l2,l3间的距离为3,则AB的长度为( )
A.2 B.3 C.4 D.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,∠C=90°,如果AC=1,∠B=30°,那么AB=________,BC=________.
12.如图,在△ABC中,∠C=90°,BA=15,AC=12,以直角边BC为直径作半圆,则这个半圆的面积是________.
第12题图 第13题图 第14题图
13.《九章算术》中记载:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”译文:有一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,线段OB表示竹梢触地面处与竹根的距离,则竹子折断处离地面的高度OA是________尺.
14.如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它爬行的路径是最短的,那么最短距离为________.
三、(本大题共2小题,每小题8分,满分16分)
15.已知a,b,c为一个直角三角形的三边长,且有+(b-2)2=0,求直角三角形的斜边长.
16.如图,有一块边长为40米的正方形绿地ABCD,在绿地的边BC上的E处装有健身器材,BE=9米.有人为了走近路,从A处直接踏过绿地到达E处,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题:
(1)线段AB的长为________,BC的长为________,CD的长为________;
(2)连接AC,通过计算说明△ACD和△ABC各是什么特殊三角形.
18.如图,在四边形ABCD中,∠B=90°,AB=2,BC=4,CD=5,AD=3,求四边形ABCD的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1……如此作下去,若OA=OB=1.
(1)A1B=________,S△A1B1A2=________;
(2)试猜想第n个等腰直角三角形的面积Sn.
20.如图,在笔直的铁路上A,B两点相距25km,C,D为两村庄,DA=10km,CB=15km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.求E站应建在距点A多远处.
六、(本题满分12分)
21.如图,在△ABC中,AB=8cm,AC=6cm,BC=10cm,点D在AB上,且BD=CD,求△BDC的面积.
七、(本题满分12分)
22.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?
八、(本题满分14分)
23.定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位长度)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”?如果能,请画出示意图;如果不能,请说明理由.
①摆出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
参考答案与解析
1.B 2.D 3.A 4.B 5.D 6.D 7.C 8.A
9.B 解析:由题意得两式相减得2xy=45,∴2xy+4=49,x2+2xy+y2=94,∴(x+y)2=94,∴x+y=.∵(x-y)2=4,x>y,∴x-y=2,∴①②③正确,④错误.故选B.
10.D 解析:过点A作AD⊥l3于点D,过点B作BE⊥l3于点E,则AD=1+3=4,BE=3,∠ADC=∠CEB=90°,∴∠CAD+∠ACD=90°.∵△ABC是等腰直角三角形,∴AC=BC,∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠CAD=∠BCE.在△ADC和△CEB中,∵∴△ADC≌△CEB,∴CD=BE=3.在Rt△ADC中,由勾股定理得AC==5.∴BC=AC=5,∴AB==5.故选D.
11.2 12. 13.4.55
14.2 解析:将正方体表面按如图展开,连接AB,此时蚂蚁运动的路径AB最短.易知AD=2×3=6,BD=2,则最短距离AB==2.
15.解:∵+(b-2)2=0,∴a-3=0,b-2=0,解得a=3,b=2.(3分)①以a为斜边长时,斜边长为3;(5分)②以a,b为直角边的长时,斜边长为=.(7分)综上所述,直角三角形的斜边长为3或.(8分)
16.解:∵正方形ABCD的边长为40米,∴AB=40米,∠B=90°.在Rt△ABE中,由勾股定理得AE===41(米).(4分)∵AB+BE=40+9=49(米),∴少走的路程为49-41=8(米),∴标牌的■处填的数是8.(8分)
17.解:(1) 5 2(3分)
(2)∵AC==2,AD==2,∴AC=AD,∴△ACD是等腰三角形.(5分)∵AB2+AC2=()2+(2)2=5+20=25=BC2,∴△ABC是直角三角形.(8分)
18.解:连接AC.在Rt△ABC中,AC===2.(2分)∵AC2+CD2=(2)2+52=45=(3)2=AD2,∴∠ACD=90°,(4分)∴S四边形ABCD=AB·BC+AC·CD=×2×4+×2×5=4+5.(8分)
19.解:(1)2(2分) 4(4分)
(2)∵OA=OB=1,∠AOB=90°,∴AB=,S1=×1×1==2-1.∵AA1=AB=,∠A1AB=90°,∴A1B=2,S2=××=1=20.∵BB1=A1B=2,∠A1BB1=90°,∴A1B1=2,S3=×2×2=2=21.∵A2A1=A1B1=2,∠A2A1B1=90°,∴A2B1=4,S4=×2×2=4=22.由此可猜想Sn=2n-2.(10分)
20.解:设AE=xkm,则BE=(25-x)km.(2分)在Rt△ADE中,由勾股定理得DE2=AD2+AE2=102+x2.在Rt△BCE中,由勾股定理得CE2=BC2+BE2=152+(25-x)2.(6分)由题意可知DE=CE,即102+x2=152+(25-x)2,解得x=15.(9分)
答:E站应建在距点A15km处.(10分)
21.解:∵AB=8cm,AC=6cm,BC=10cm,∴AB2+AC2=BC2,∴∠BAC=90°.(3分)设BD=CD=xcm,则AD=(8-x)cm.(5分)在Rt△ADC中,由勾股定理得AD2+AC2=CD2,即(8-x)2+62=x2,解得x=,即BD=cm.(9分)∴S△BDC=BD·AC=××6=(cm2).(12分)
22.解:(1)如图为圆柱侧面沿AB剪开的展开图.(1分)圆柱的底面周长为30cm,即AC=30cm,高为40cm,即CD=40cm,∴AD==50cm.(5分)
答:它爬行一圈的路程是50cm.(6分)
(2)树干的周长为80cm,即AC=80cm,绕一圈爬行100cm,即AD=100cm,∴绕一圈上升的高度CD==60cm.(10分)∴树干的高为60×10=600(cm)=6(m).(11分)
答:树干高6m.(12分)
23.解:(1)小颖摆出如图①所示的“整数三角形”,(4分)
小辉摆出如图②所示三个不同的等腰“整数三角形”.(10分)
(2)①不能摆出等边“整数三角形”.理由如下:设等边三角形的边长为a,易得等边三角形的面积为a2.若边长a为整数,那么面积a2一定是非整数.所以不存在等边“整数三角形”.(12分)
②能摆出一个非特殊“整数三角形”,如图③所示.(14分)
时间:120分钟 满分:150分
题号
一
二
三
四
五
六
七
八
总分
得分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.设直角三角形的两条直角边的长分别为a和b,斜边长为c,已知b=12,c=13,则a的值为( )
A.1 B.5 C.10 D.25
2.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
A.1,, B.6,8,10
C.5,12,13 D.,2,
3.如图,点P是平面坐标系内一点,则点P到原点的距离是( )
A.3 B. C. D.
第3题图 第4题图
4.如图,已知AB⊥CD,△ABD,△BCE都是等腰直角三角形.如果CD=7,BE=3,那么AC的长为( )
A.8 B.5 C.3 D.4
5.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
A.60海里 B.45海里
C.20海里 D.30海里
第5题图 第6题图
6.如图是一个十字路口,O是两条公路的交点,点A,B,C,D表示的是公路上的四辆车.若OC=8m,AC=17m,AB=5m,BD=10m,则C,D两辆车之间的距离为( )
A.5m B.4m C.3m D.2m
7.如图,在Rt△ABC中,∠ACB=90°,若AB=15cm,则正方形ADEC与正方形BCFG的面积之和为( )
A.150cm2 B.200cm2 C.225cm2 D.无法计算
第7题图 第8题图
8.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线AC上的D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4.若用x,y表示直角三角形的两直角边长(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9.其中正确的说法是( )
A.①② B.①②③
C.①②④ D.①②③④
第 9题图 第10题图
10.如图,已知等腰直角三角形ABC的各顶点分别在直线l1,l2,l3上,且l1∥l2∥l3,l1,l2间的距离为1,l2,l3间的距离为3,则AB的长度为( )
A.2 B.3 C.4 D.5
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,∠C=90°,如果AC=1,∠B=30°,那么AB=________,BC=________.
12.如图,在△ABC中,∠C=90°,BA=15,AC=12,以直角边BC为直径作半圆,则这个半圆的面积是________.
第12题图 第13题图 第14题图
13.《九章算术》中记载:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”译文:有一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,线段OB表示竹梢触地面处与竹根的距离,则竹子折断处离地面的高度OA是________尺.
14.如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它爬行的路径是最短的,那么最短距离为________.
三、(本大题共2小题,每小题8分,满分16分)
15.已知a,b,c为一个直角三角形的三边长,且有+(b-2)2=0,求直角三角形的斜边长.
16.如图,有一块边长为40米的正方形绿地ABCD,在绿地的边BC上的E处装有健身器材,BE=9米.有人为了走近路,从A处直接踏过绿地到达E处,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题:
(1)线段AB的长为________,BC的长为________,CD的长为________;
(2)连接AC,通过计算说明△ACD和△ABC各是什么特殊三角形.
18.如图,在四边形ABCD中,∠B=90°,AB=2,BC=4,CD=5,AD=3,求四边形ABCD的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1……如此作下去,若OA=OB=1.
(1)A1B=________,S△A1B1A2=________;
(2)试猜想第n个等腰直角三角形的面积Sn.
20.如图,在笔直的铁路上A,B两点相距25km,C,D为两村庄,DA=10km,CB=15km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.求E站应建在距点A多远处.
六、(本题满分12分)
21.如图,在△ABC中,AB=8cm,AC=6cm,BC=10cm,点D在AB上,且BD=CD,求△BDC的面积.
七、(本题满分12分)
22.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?
八、(本题满分14分)
23.定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位长度)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”?如果能,请画出示意图;如果不能,请说明理由.
①摆出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
参考答案与解析
1.B 2.D 3.A 4.B 5.D 6.D 7.C 8.A
9.B 解析:由题意得两式相减得2xy=45,∴2xy+4=49,x2+2xy+y2=94,∴(x+y)2=94,∴x+y=.∵(x-y)2=4,x>y,∴x-y=2,∴①②③正确,④错误.故选B.
10.D 解析:过点A作AD⊥l3于点D,过点B作BE⊥l3于点E,则AD=1+3=4,BE=3,∠ADC=∠CEB=90°,∴∠CAD+∠ACD=90°.∵△ABC是等腰直角三角形,∴AC=BC,∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠CAD=∠BCE.在△ADC和△CEB中,∵∴△ADC≌△CEB,∴CD=BE=3.在Rt△ADC中,由勾股定理得AC==5.∴BC=AC=5,∴AB==5.故选D.
11.2 12. 13.4.55
14.2 解析:将正方体表面按如图展开,连接AB,此时蚂蚁运动的路径AB最短.易知AD=2×3=6,BD=2,则最短距离AB==2.
15.解:∵+(b-2)2=0,∴a-3=0,b-2=0,解得a=3,b=2.(3分)①以a为斜边长时,斜边长为3;(5分)②以a,b为直角边的长时,斜边长为=.(7分)综上所述,直角三角形的斜边长为3或.(8分)
16.解:∵正方形ABCD的边长为40米,∴AB=40米,∠B=90°.在Rt△ABE中,由勾股定理得AE===41(米).(4分)∵AB+BE=40+9=49(米),∴少走的路程为49-41=8(米),∴标牌的■处填的数是8.(8分)
17.解:(1) 5 2(3分)
(2)∵AC==2,AD==2,∴AC=AD,∴△ACD是等腰三角形.(5分)∵AB2+AC2=()2+(2)2=5+20=25=BC2,∴△ABC是直角三角形.(8分)
18.解:连接AC.在Rt△ABC中,AC===2.(2分)∵AC2+CD2=(2)2+52=45=(3)2=AD2,∴∠ACD=90°,(4分)∴S四边形ABCD=AB·BC+AC·CD=×2×4+×2×5=4+5.(8分)
19.解:(1)2(2分) 4(4分)
(2)∵OA=OB=1,∠AOB=90°,∴AB=,S1=×1×1==2-1.∵AA1=AB=,∠A1AB=90°,∴A1B=2,S2=××=1=20.∵BB1=A1B=2,∠A1BB1=90°,∴A1B1=2,S3=×2×2=2=21.∵A2A1=A1B1=2,∠A2A1B1=90°,∴A2B1=4,S4=×2×2=4=22.由此可猜想Sn=2n-2.(10分)
20.解:设AE=xkm,则BE=(25-x)km.(2分)在Rt△ADE中,由勾股定理得DE2=AD2+AE2=102+x2.在Rt△BCE中,由勾股定理得CE2=BC2+BE2=152+(25-x)2.(6分)由题意可知DE=CE,即102+x2=152+(25-x)2,解得x=15.(9分)
答:E站应建在距点A15km处.(10分)
21.解:∵AB=8cm,AC=6cm,BC=10cm,∴AB2+AC2=BC2,∴∠BAC=90°.(3分)设BD=CD=xcm,则AD=(8-x)cm.(5分)在Rt△ADC中,由勾股定理得AD2+AC2=CD2,即(8-x)2+62=x2,解得x=,即BD=cm.(9分)∴S△BDC=BD·AC=××6=(cm2).(12分)
22.解:(1)如图为圆柱侧面沿AB剪开的展开图.(1分)圆柱的底面周长为30cm,即AC=30cm,高为40cm,即CD=40cm,∴AD==50cm.(5分)
答:它爬行一圈的路程是50cm.(6分)
(2)树干的周长为80cm,即AC=80cm,绕一圈爬行100cm,即AD=100cm,∴绕一圈上升的高度CD==60cm.(10分)∴树干的高为60×10=600(cm)=6(m).(11分)
答:树干高6m.(12分)
23.解:(1)小颖摆出如图①所示的“整数三角形”,(4分)
小辉摆出如图②所示三个不同的等腰“整数三角形”.(10分)
(2)①不能摆出等边“整数三角形”.理由如下:设等边三角形的边长为a,易得等边三角形的面积为a2.若边长a为整数,那么面积a2一定是非整数.所以不存在等边“整数三角形”.(12分)
②能摆出一个非特殊“整数三角形”,如图③所示.(14分)
