沪科版数学八年级下册第二十章 数据的初步分析 检测卷(含答案)
文档属性
| 名称 | 沪科版数学八年级下册第二十章 数据的初步分析 检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 00:00:00 | ||
图片预览



文档简介
沪科版数学八年级下册第二十章检测卷
时间:120分钟 满分:150分
题号
一
二
三
四
五
总分
得分
一、选择题(本大题共10小题,每小题5分,满分50分)
1.某样本容量是60,分组后第2组的频率是0.15,那么第2组的频数是( )
A.9 B.18 C.60 D.400
2.一组数据6,3,9,4,3,5,12的中位数是( )
A.3 B.4 C.5 D.6
3.某市气象部门测得某周七天的日温差数据如下(单位:℃):4,6,6,5,7,6,8,这组数据的平均数和众数分别是( )
A.7,6 B.6,5 C.5,6 D.6,6
4.将样本容量为100的样本编制成组号①~⑧的八个组,简况如下表所示:
组号
①
②
③
④
⑤
⑥
⑦
⑧
频数
14
11
12
13
■
13
12
10
那么第⑤组的频率是( )
A.14 B.15 C.0.14 D.0.15
5.某校为了解全校同学“五一”假期参加社团活动的情况,抽查了100名同学,统计他们假期参加社团活动的时间,绘成频数直方图(如图),则参加社团活动时间的中位数所在的范围是( )
A.4~6小时
B.6~8小时
C.8~10小时
D.不能确定
6.“莲城读书月”活动结束后,对八(3)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量
1本
2本
3本
3本以上
人数
10
18
13
4
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
平均数 B.中位数 C.众数 D.方差
7.若一组数据3,x,4,5,6的众数为6,则这组数据的中位数为( )
A.3 B.4 C.5 D.6
8.某科普小组有5名成员,身高(单位:cm)分别为:160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数不变,方差不变 B.平均数不变,方差变大
C.平均数不变,方差变小 D.平均数变小,方差不变
甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如下表所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
A.甲 B.乙 C.丙 D.丁
10.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5, B.5,5,10 C.6,5.5, D.5,5,
二、填空题(本大题共4小题,每小题5分,满分20分)
某食堂午餐供应10元、16元、20元三种价格的盒饭,根据食堂某月销售午餐盒饭的统计图(如图),可计算出该月食堂午餐盒饭的平均价格是________元.
12.甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为s=0.9,s=1.1,则甲、乙两支仪仗队的队员身高更整齐的是________(填“甲”或“乙”).
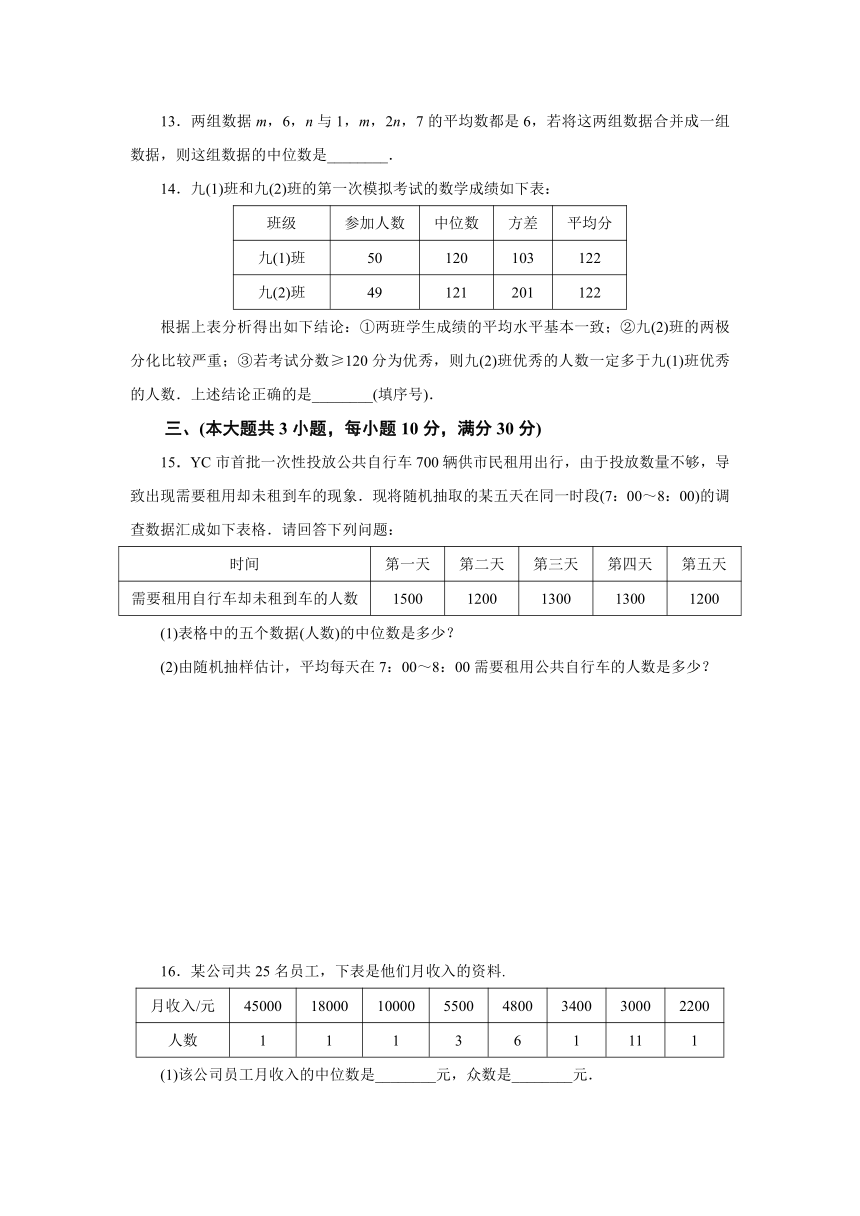
13.两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组数据的中位数是________.
14.九(1)班和九(2)班的第一次模拟考试的数学成绩如下表:
班级
参加人数
中位数
方差
平均分
九(1)班
50
120
103
122
九(2)班
49
121
201
122
根据上表分析得出如下结论:①两班学生成绩的平均水平基本一致;②九(2)班的两极分化比较严重;③若考试分数≥120分为优秀,则九(2)班优秀的人数一定多于九(1)班优秀的人数.上述结论正确的是________(填序号).
三、(本大题共3小题,每小题10分,满分30分)
15.YC市首批一次性投放公共自行车700辆供市民租用出行,由于投放数量不够,导致出现需要租用却未租到车的现象.现将随机抽取的某五天在同一时段(7:00~8:00)的调查数据汇成如下表格.请回答下列问题:
时间
第一天
第二天
第三天
第四天
第五天
需要租用自行车却未租到车的人数
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00~8:00需要租用公共自行车的人数是多少?
16.某公司共25名员工,下表是他们月收入的资料.
月收入/元
45000
18000
10000
5500
4800
3400
3000
2200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是________元,众数是________元.
(2)根据上表,可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
17.为了从甲、乙两名运动员中选拔一人参加市射击比赛,在选拔赛上每人打10发,其中甲的射击环数分别是10,8,7,9,8,10,10,9,10,9.
(1)计算甲射击成绩的方差;
(2)经过统计,乙射击的平均成绩是9,方差是1.4,你认为选谁去参加比赛更合适?为什么?
四、(本大题共3小题,每小题12分,满分36分)
18.某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分(百分制)如下表.
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,并按60%、30%、10%的比例计入总分.根据规定,请你说明谁将被录用.
,笔试,面试,体能
甲,83,79,90
乙,85,80,75
丙,80,90,73
19.在“不闯红灯,珍惜生命”活动中,文明中学的关欣和李好同学某天来到城区中心的十字路口观察,统计上午7:00~12:00中闯红灯的人次,制作了两个数据统计图(如图).
(1)求图①提供的五个数据(各时段闯红灯人次)的众数和平均数;
(2)估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有________人次;
(3)请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
20.中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如下所示:
(1)统计表中的a=________,b=________,c=________;
(2)请将频数直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你估计该校八年级学生课外阅读7本及以上的人数.
五、(本题满分14分)
21.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下:
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(1)求出上面成绩统计分析表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
参考答案与解析
1.A 2.C 3.D 4.D 5.B 6.C 7.C 8.C 9.C 10.D
11.13 12.甲
13.7 解析:由题意得解得两组数据合并后从小到大排列为1,4,6,7,8,8,8,中位数为7.
14.①② 解析:由平均数相同可得两班学生成绩的平均水平基本一致,故①正确;因为九(1)班的方差103小于九(2)班的方差201,所以九(2)班的两极分化比较严重,故②正确;因为九(2)班的学生比九(1)班的学生人数少一人,根据九(1)班的中位数为120,九(2)班的中位数为121,无法判断九(2)班的优秀人数一定比九(1)班多,故③错误.故答案为①②.
15.解:(1)表格中5个数据按从小到大的顺序排列为1200,1200,1300,1300,1500,所以中位数是1300.(3分)
(2)抽取的五天平均每天在7:00~8:00需要租用自行车却未租到车的人数为(1500+1200+1300+1300+1200)÷5=1300(人).(6分)∵YC市首批一次性投放公共自行车700辆供市民租用出行,∴估计平均每天在7:00~8:00需要租用公共自行车的人数是1300+700=2000(人).(9分)
答:平均每天在7:00~8:00需要租用公共自行车的人数约为2000.(10分)
16.解:(1)3400 3000(5分)
(2)用中位数或众数来描述较为合适.(7分)理由如下:平均数受极端值45000元的影响,只有3个人的工资在6276元以上,所以用平均数反映该公司全体员工月收入水平不合适.而中位数或众数反映了该公司多数员工的月收入水平,所以用中位数或众数来描述较为合适.(10分)
17.解:(1)x甲=(10+8+7+9+8+10+10+9+10+9)=9,(2分)s=[(10-9)2+(8-9)2+(7-9)2+…+(9-9)2]=1.(5分)
(2)选甲去参加比赛更合适.(7分)理由如下:甲、乙两人的平均成绩相同,说明两人成绩相当.但甲射击成绩的方差较小,说明甲的射击成绩更稳定,故选甲去参加比赛更合适.(10分)
18.解:(1)x甲=(83+79+90)÷3=84(分),x乙=(85+80+75)÷3=80(分),x丙=(80+90+73)÷3=81(分).从高到低确定三名应聘者的排名顺序为甲、丙、乙.(6分)
(2)∵该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,∴甲淘汰.乙的成绩为85×60%+80×30%+75×10%=82.5(分),丙的成绩为80×60%+90×30%+73×10%=82.3(分).∵82.5>82.3,∴乙将被录用.(12分)
19.解:(1)众数为15,平均数为=20.(6分)
(2)1050(9分)
(3)只要提的建议合理即可.如:①加强对中午下班高峰期的道路管理;②中青年人闯红灯人数多,要加强对中青年人交通规则的教育.(12分)
20.解:(1)10 0.28 50(3分)
(2)补全频数直方图如图所示.(6分)
(3)=6.4(本).(8分)
答:所有被调查学生课外阅读的平均本数为6.4本.(9分)
(4)1200×(0.28+0.16)=528(人).(11分)
答:估计该校八年级学生课外阅读7本及以上的人数约为528人.(12分)
21.解:(1)由折线统计图可知,甲组成绩从小到大排列为3、6、6、6、6、6、7、9、9、10,则中位数a=6.(3分)乙组学生成绩的平均分b==7.2.(6分)
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩7分在小组中排名属中游略偏上,∴小英是甲组学生.(10分)
(3)理由如下:①乙组的平均分高于甲组,即乙组的总体平均水平高.②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.(14分)
时间:120分钟 满分:150分
题号
一
二
三
四
五
总分
得分
一、选择题(本大题共10小题,每小题5分,满分50分)
1.某样本容量是60,分组后第2组的频率是0.15,那么第2组的频数是( )
A.9 B.18 C.60 D.400
2.一组数据6,3,9,4,3,5,12的中位数是( )
A.3 B.4 C.5 D.6
3.某市气象部门测得某周七天的日温差数据如下(单位:℃):4,6,6,5,7,6,8,这组数据的平均数和众数分别是( )
A.7,6 B.6,5 C.5,6 D.6,6
4.将样本容量为100的样本编制成组号①~⑧的八个组,简况如下表所示:
组号
①
②
③
④
⑤
⑥
⑦
⑧
频数
14
11
12
13
■
13
12
10
那么第⑤组的频率是( )
A.14 B.15 C.0.14 D.0.15
5.某校为了解全校同学“五一”假期参加社团活动的情况,抽查了100名同学,统计他们假期参加社团活动的时间,绘成频数直方图(如图),则参加社团活动时间的中位数所在的范围是( )
A.4~6小时
B.6~8小时
C.8~10小时
D.不能确定
6.“莲城读书月”活动结束后,对八(3)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量
1本
2本
3本
3本以上
人数
10
18
13
4
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
平均数 B.中位数 C.众数 D.方差
7.若一组数据3,x,4,5,6的众数为6,则这组数据的中位数为( )
A.3 B.4 C.5 D.6
8.某科普小组有5名成员,身高(单位:cm)分别为:160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数不变,方差不变 B.平均数不变,方差变大
C.平均数不变,方差变小 D.平均数变小,方差不变
甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如下表所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
A.甲 B.乙 C.丙 D.丁
10.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5, B.5,5,10 C.6,5.5, D.5,5,
二、填空题(本大题共4小题,每小题5分,满分20分)
某食堂午餐供应10元、16元、20元三种价格的盒饭,根据食堂某月销售午餐盒饭的统计图(如图),可计算出该月食堂午餐盒饭的平均价格是________元.
12.甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为s=0.9,s=1.1,则甲、乙两支仪仗队的队员身高更整齐的是________(填“甲”或“乙”).
13.两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组数据的中位数是________.
14.九(1)班和九(2)班的第一次模拟考试的数学成绩如下表:
班级
参加人数
中位数
方差
平均分
九(1)班
50
120
103
122
九(2)班
49
121
201
122
根据上表分析得出如下结论:①两班学生成绩的平均水平基本一致;②九(2)班的两极分化比较严重;③若考试分数≥120分为优秀,则九(2)班优秀的人数一定多于九(1)班优秀的人数.上述结论正确的是________(填序号).
三、(本大题共3小题,每小题10分,满分30分)
15.YC市首批一次性投放公共自行车700辆供市民租用出行,由于投放数量不够,导致出现需要租用却未租到车的现象.现将随机抽取的某五天在同一时段(7:00~8:00)的调查数据汇成如下表格.请回答下列问题:
时间
第一天
第二天
第三天
第四天
第五天
需要租用自行车却未租到车的人数
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00~8:00需要租用公共自行车的人数是多少?
16.某公司共25名员工,下表是他们月收入的资料.
月收入/元
45000
18000
10000
5500
4800
3400
3000
2200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是________元,众数是________元.
(2)根据上表,可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
17.为了从甲、乙两名运动员中选拔一人参加市射击比赛,在选拔赛上每人打10发,其中甲的射击环数分别是10,8,7,9,8,10,10,9,10,9.
(1)计算甲射击成绩的方差;
(2)经过统计,乙射击的平均成绩是9,方差是1.4,你认为选谁去参加比赛更合适?为什么?
四、(本大题共3小题,每小题12分,满分36分)
18.某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分(百分制)如下表.
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,并按60%、30%、10%的比例计入总分.根据规定,请你说明谁将被录用.
,笔试,面试,体能
甲,83,79,90
乙,85,80,75
丙,80,90,73
19.在“不闯红灯,珍惜生命”活动中,文明中学的关欣和李好同学某天来到城区中心的十字路口观察,统计上午7:00~12:00中闯红灯的人次,制作了两个数据统计图(如图).
(1)求图①提供的五个数据(各时段闯红灯人次)的众数和平均数;
(2)估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有________人次;
(3)请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
20.中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如下所示:
(1)统计表中的a=________,b=________,c=________;
(2)请将频数直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你估计该校八年级学生课外阅读7本及以上的人数.
五、(本题满分14分)
21.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下:
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(1)求出上面成绩统计分析表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
参考答案与解析
1.A 2.C 3.D 4.D 5.B 6.C 7.C 8.C 9.C 10.D
11.13 12.甲
13.7 解析:由题意得解得两组数据合并后从小到大排列为1,4,6,7,8,8,8,中位数为7.
14.①② 解析:由平均数相同可得两班学生成绩的平均水平基本一致,故①正确;因为九(1)班的方差103小于九(2)班的方差201,所以九(2)班的两极分化比较严重,故②正确;因为九(2)班的学生比九(1)班的学生人数少一人,根据九(1)班的中位数为120,九(2)班的中位数为121,无法判断九(2)班的优秀人数一定比九(1)班多,故③错误.故答案为①②.
15.解:(1)表格中5个数据按从小到大的顺序排列为1200,1200,1300,1300,1500,所以中位数是1300.(3分)
(2)抽取的五天平均每天在7:00~8:00需要租用自行车却未租到车的人数为(1500+1200+1300+1300+1200)÷5=1300(人).(6分)∵YC市首批一次性投放公共自行车700辆供市民租用出行,∴估计平均每天在7:00~8:00需要租用公共自行车的人数是1300+700=2000(人).(9分)
答:平均每天在7:00~8:00需要租用公共自行车的人数约为2000.(10分)
16.解:(1)3400 3000(5分)
(2)用中位数或众数来描述较为合适.(7分)理由如下:平均数受极端值45000元的影响,只有3个人的工资在6276元以上,所以用平均数反映该公司全体员工月收入水平不合适.而中位数或众数反映了该公司多数员工的月收入水平,所以用中位数或众数来描述较为合适.(10分)
17.解:(1)x甲=(10+8+7+9+8+10+10+9+10+9)=9,(2分)s=[(10-9)2+(8-9)2+(7-9)2+…+(9-9)2]=1.(5分)
(2)选甲去参加比赛更合适.(7分)理由如下:甲、乙两人的平均成绩相同,说明两人成绩相当.但甲射击成绩的方差较小,说明甲的射击成绩更稳定,故选甲去参加比赛更合适.(10分)
18.解:(1)x甲=(83+79+90)÷3=84(分),x乙=(85+80+75)÷3=80(分),x丙=(80+90+73)÷3=81(分).从高到低确定三名应聘者的排名顺序为甲、丙、乙.(6分)
(2)∵该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,∴甲淘汰.乙的成绩为85×60%+80×30%+75×10%=82.5(分),丙的成绩为80×60%+90×30%+73×10%=82.3(分).∵82.5>82.3,∴乙将被录用.(12分)
19.解:(1)众数为15,平均数为=20.(6分)
(2)1050(9分)
(3)只要提的建议合理即可.如:①加强对中午下班高峰期的道路管理;②中青年人闯红灯人数多,要加强对中青年人交通规则的教育.(12分)
20.解:(1)10 0.28 50(3分)
(2)补全频数直方图如图所示.(6分)
(3)=6.4(本).(8分)
答:所有被调查学生课外阅读的平均本数为6.4本.(9分)
(4)1200×(0.28+0.16)=528(人).(11分)
答:估计该校八年级学生课外阅读7本及以上的人数约为528人.(12分)
21.解:(1)由折线统计图可知,甲组成绩从小到大排列为3、6、6、6、6、6、7、9、9、10,则中位数a=6.(3分)乙组学生成绩的平均分b==7.2.(6分)
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩7分在小组中排名属中游略偏上,∴小英是甲组学生.(10分)
(3)理由如下:①乙组的平均分高于甲组,即乙组的总体平均水平高.②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.(14分)
