鲁教版六年级数学下册第七章相交线与平行线测试题(含答案)
文档属性
| 名称 | 鲁教版六年级数学下册第七章相交线与平行线测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 12:12:28 | ||
图片预览



文档简介
第七章 相交线与平行线测试题
一、选择题
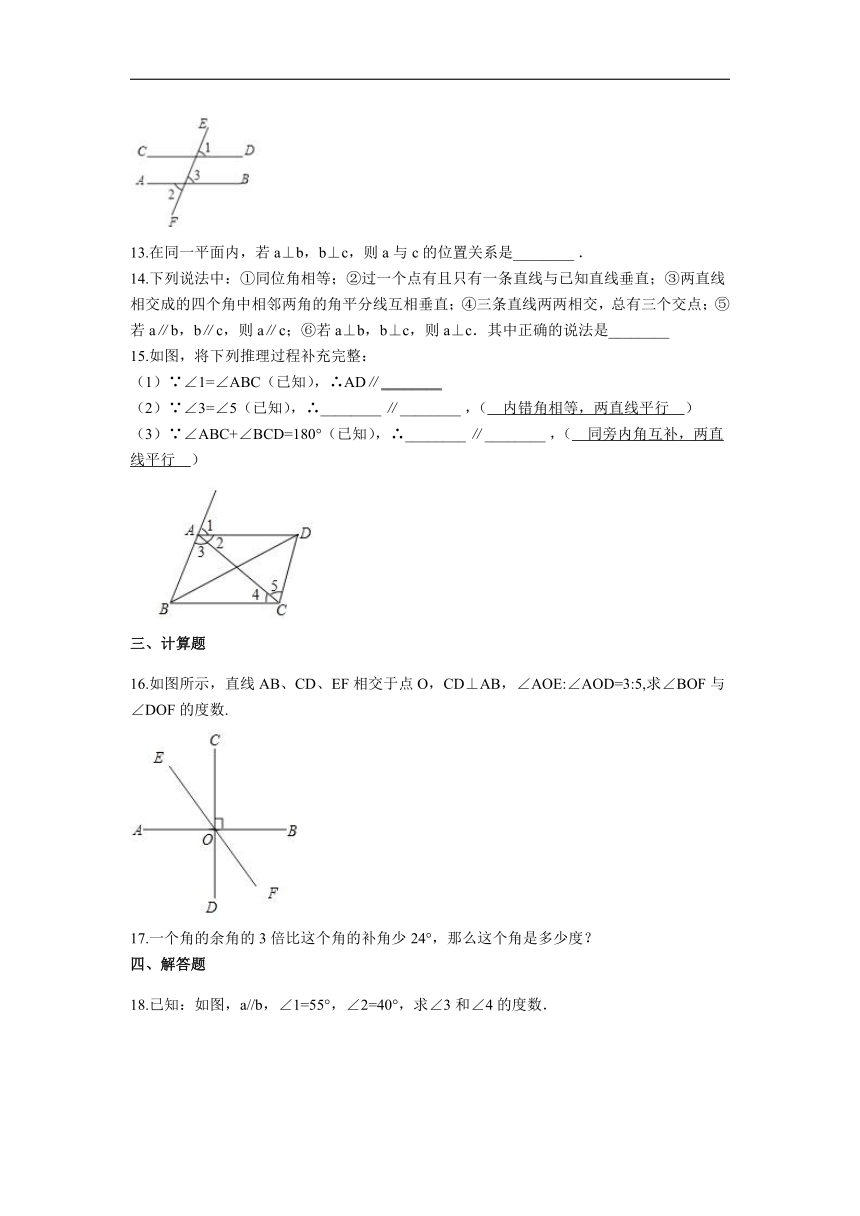
1.如图,AD⊥BC,DE∥AB,则∠B和∠1的关系是( )
?
A.?相等?????????????????????????????????B.?互补????????????????????????C.?互余??????????????????????????????????D.?不能确定
2.下列图形中 与 是内错角的是(?? )
A.???B.?C.????D.?
3.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.点P关于x轴的对称点P′的坐标为(a,b),则a与b的数量关系为( )
?
A.?a+b=0??????????????????????????????B.?a+b>0??????????????????????????C.?a﹣b=0?????????????????????????D.?a﹣b>0
4.如图,从位置P到直线公路MN共有四条小道,若用相同的速度行走,能最快到达公路MN的小道是(?? )
A.?PA????????????????????????????????????????B.?PB????????????????????????????????C.?PC????????????????????????????????D.?PD
5.已知直线 ,将一块含 角的直角三角板ABC按如图方式放置 ,其中A,B两点分别落在直线m,n上,若 ,则 的度数为( ??)
A.????????????????????????????????B.?????????????????????????????C.?????????????????????????????????D.?
6.下列说法不正确的是( )
A.?过任意一点可作已知直线的一条平行线
B.?同一平面内两条不相交的直线是平行线
C.?在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.?平行于同一直线的两直线平行
7.下列语句:①同一平面上,三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )
A.?①、②是正确的命题????????? ??B.?②、③是正确命题????????
?C.?①、③是正确命题??????? ???D.?以上结论皆错
8.下列说法:①垂线段最短;②两条直线不平行必相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且只有一条直线与已知直线平行。其中正确的有(????)
A.?1个?????????????????????????????B.?2个????????????????????????????????C.?3个??????????????????????????????????D.?4个
二、填空题
9.一个角的余角比这个角的补角的一半小40°,则这个角为________?度.
10.如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有________(填序号).
11.如图,∠1=80°,∠2=100°,∠3=76°,则∠4的度数是________度.
12.如图,∠1=∠2=35°,则AB与CD的关系是________?,理由是________?.
13.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是________?.
14.下列说法中:①同位角相等;②过一个点有且只有一条直线与已知直线垂直;③两直线相交成的四个角中相邻两角的角平分线互相垂直;④三条直线两两相交,总有三个交点;⑤若a∥b,b∥c,则a∥c;⑥若a⊥b,b⊥c,则a⊥c.其中正确的说法是________?
15.如图,将下列推理过程补充完整:
(1)∵∠1=∠ABC(已知),∴AD∥________
(2)∵∠3=∠5(已知),∴________?∥________?,( 内错角相等,两直线平行 )
(3)∵∠ABC+∠BCD=180°(已知),∴________?∥________?,( 同旁内角互补,两直线平行 )
三、计算题
16.如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与
∠DOF的度数.
17.一个角的余角的3倍比这个角的补角少24°,那么这个角是多少度?
四、解答题
18.已知:如图,a//b,∠1=55°,∠2=40°,求∠3和∠4的度数.
19.已知AC∥BD,∠CAE=30°,∠DBE=45°,求∠AEB的度数.
五、综合题
20.直线AB∥CD,E为直线AB、CD之间的一点.
(1)如图1,若∠B=15°,∠BED=90°,则∠D=________°;
(2)如图2,若∠B=α,∠D=β,则∠BED=________;
(3)如图3,若∠B=α,∠C=β,则α、β与∠BEC之间有什么等量关系?请猜想证明.
21.如图所示,BF、DE相交于点A,BG交BF于点B,交AC于点C.
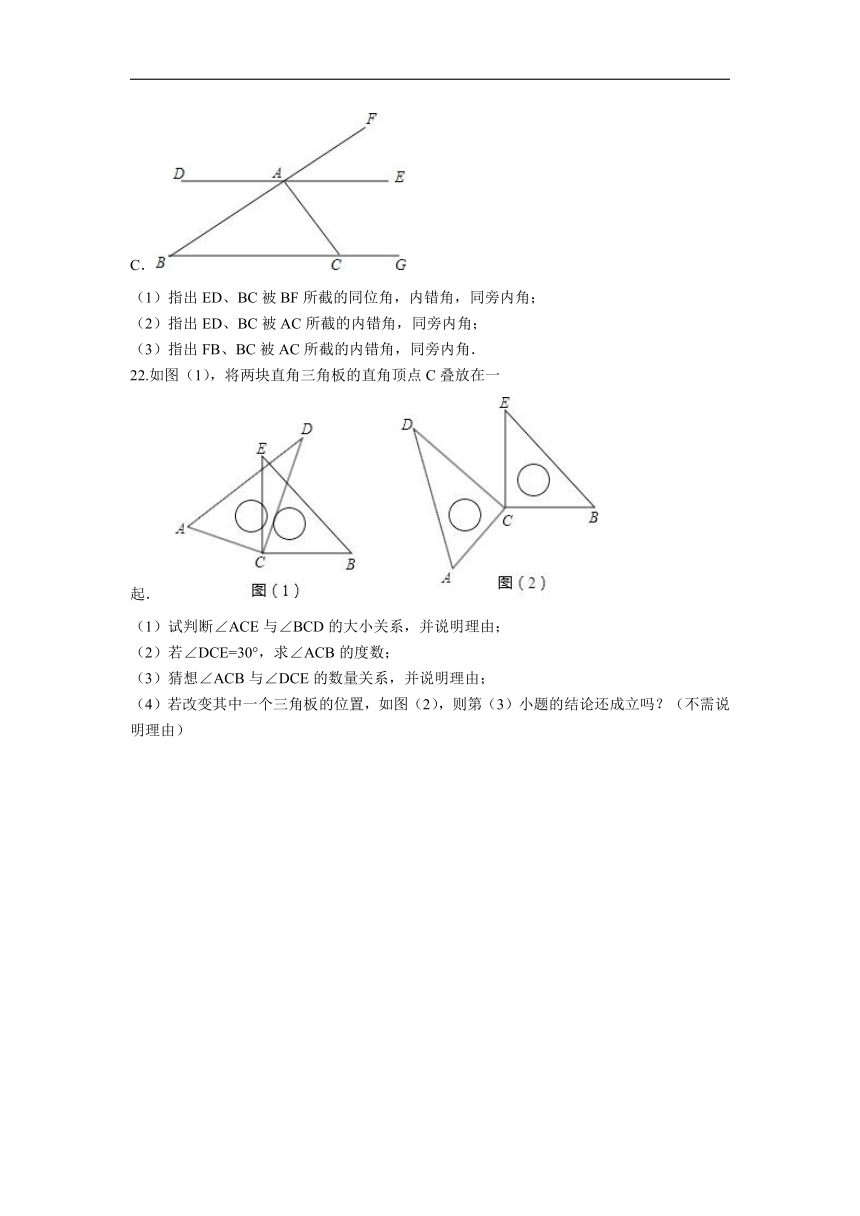
(1)指出ED、BC被BF所截的同位角,内错角,同旁内角;
(2)指出ED、BC被AC所截的内错角,同旁内角;
(3)指出FB、BC被AC所截的内错角,同旁内角.
22.如图(1),将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
答案解析部分
一、单选题
1.【答案】C
【考点】余角和补角
【解析】【解答】解:∵DE∥AB,
∴∠B=∠EDC,
∵AD⊥BC,
∴∠1+∠EDC=90°,
∴∠B+∠1=90°,
∴∠B和∠1互余.
故选:C.
【分析】由DE∥AB,得出∠B=∠EDC,由AD⊥BC,得出∠1+∠EDC=90°,即可得出∴∠B和∠1互余.
2.【答案】A
【考点】同位角、内错角、同旁内角
【解析】【解答】解:A. ∠2与∠1是内错角,故此选项正确;
B. ∠2与∠1的对顶角是同位角,故此选项错误;
C. ∠2与∠1 是同旁内角,故此选项错误;
D. ∠2与∠1的邻补角是内错角,故此选项错误;
故选:A.
【分析】本题主要考查的知识点为内错角,两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角.掌握内错角的定义是解答本题的关键.
3.【答案】C
【考点】作图—基本作图
【解析】【解答】解:根据作图方法可得点P在第二象限角平分线上;点P到x轴、y轴的距离相等;
∵点P关于x轴的对称点P′的坐标为(a,b),
∴P(a,﹣b),
故a﹣b=0.
故选:C.
【分析】根据作图方法可得点P在第二象限的角平分线上,根据角平分线的性质和第二象限内点的坐标符号可得答案.
4.【答案】B
【考点】垂线段最短
【解析】【解答】根据垂线段最短得,能最快到达公路MN的小道是PB,
故答案为:B.
【分析】依据垂线段最短进行判断即可.
5.【答案】D
【考点】平行线的性质
【解析】【解答】解:如下图,
∵∠ABC=30°,∠1=20°,
∴∠ABD=∠ABC+∠1=50°,
又∵m∥n,
∴∠2=∠ABD=50°.
故答案为:D.
【分析】根据平行线的性质即可求解。
6.【答案】A
【考点】平行线的判定
【解析】【解答】解:A中,若点在直线上,则不可以作出已知直线的平行线,而是与已知直线重合,错误.
B、C、D是公理,正确.
故选A.
【分析】根据平行线的定义及平行公理进行判断.
7.【答案】A
【考点】平行公理及推论
【解析】【解答】①同一平面上,三条直线只有两个交点,则其中两条直线互相平行,正确;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直,正确;③过直线外一点有且只有一条直线与已知直线平行,所以错误.故①、②是正确的命题,故选:A.
【分析】根据平行公理、垂直的定义和平行线的定义进行判断即可.
8.【答案】A
【考点】平行线的判定
【解析】
【分析】①根据垂线段的性质判断;
②由两条直线的关系解答;
③垂线的定义;
④由平行线的定义解答;
【解答】①直线外一点与直线上各点连接的所有线段中,垂线段最短.故该选项正确;
②同一平面内,两条直线不平行必相交,故该选项错误;
③同一平面内,过一点有且只有一条直线与已知直线垂直,故该选项错误;
④过直线外一点有且只有一条直线与已知直线平行,故该选项错误.
综上所述,说法正确的是①,共有1个.
故选A.
【点评】本题主要考查学生对各种概念公理的理解及掌握程度,是应熟记的内容
二、填空题
9.【答案】80
【考点】余角和补角
【解析】【解答】解:设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),
由题意得,(180°﹣x)﹣(90°﹣x)=40°,
解得x=80°.
故答案为:80.
【分析】设这个角为x,根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°表示出它的余角和补角,然后列出方程求解即可.
10.【答案】①③④
【考点】余角和补角
【解析】【解答】解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠AOB+∠COD不一定等于90°,故②错误;
∠BOC+∠AOD=90°﹣∠AOB+90°+∠AOB=180°,故③正确;
∠AOC﹣∠COD=∠AOC﹣∠AOB=∠BOC,故④正确;
综上所述,说法正确的是①③④.
故答案为:①③④.
【分析】根据垂直的定义和同角的余角相等分别计算,然后对各小题分析判断即可得解.
11.【答案】76
【考点】对顶角、邻补角,平行线的判定与性质
【解析】【解答】如图:
?
【分析】根据对顶角相等得出∠2=∠5,然后根据同旁内角互补,两直线平行得出∥b,再根据二直线平行,内错角相等得出∠ 3 = ∠ 4 = 76 ° ?。
12.【答案】AB∥CD;同位角相等,两直线平行
【考点】平行线的判定
【解析】【解答】解:∵∠1=∠2=35°,
∴∠3=∠2=∠1=35°,
∴AB∥CD.
故答案为:AB∥CD,同位角相等,两直线平行.
【分析】先根据对顶角相等求出∠3的度数,再由平行线的判定定理即可得出结论.
13.【答案】a∥c
【考点】平行公理及推论
【解析】【解答】解:∵a⊥b,b⊥c,
∴a∥c.
故答案为a∥c.
【分析】根据在同一平面内,垂直于同一条直线的两条直线互相平行即可求解.
14.【答案】③⑤
【考点】平行公理及推论
【解析】【解答】解:①应为:两直线平行,同位角相等,故本小题错误;
②应为:在同一平面内,过一个点有且只有一条直线与已知直线垂直,故本小题错误;
③两直线相交成的四个角中相邻两角的角平分线互相垂直,故本小题正确;
④三条直线两两相交,总有一个交点或三个交点,故本小题错误;
⑤若a∥b,b∥c,则a∥c,故本小题正确;
⑥应为:在同一平面内,若a⊥b,b⊥c,则a⊥c,故本小题错误.
综上所述,正确的有③⑤.
故答案为③⑤.
【分析】利用同位角的性质、垂线的性质、垂直的定义,两直线的位置关系以及平行公理的推论等知识分别判断后即可确定正确的答案.
15.【答案】BC;AB;CD;AB;CD
【考点】平行线的判定
【解析】【解答】解:(1))∵∠1=∠ABC(已知)
∴AD∥BC(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行;
(2)∵∠3=∠5,
∴AB∥CD(内错角相等,两直线平行).
故答案为:AB,CD;
(3))∵∠ABC+∠BCD=180°(已知)
∴AB∥CD,(同旁内角互补,两直线平行).
故答案为:AB,CD,同旁内角互补,两直线平行.
【分析】(1)根据同位角相等,两直线平行得出结论;
(2)根据内错角相等,两直线平行得出结论;
(3)根据同旁内角互补,两直线平行得出结论.
三、计算题
16.【答案】解:∵∠AOE:∠AOD=3:5,∠AOD=90°,
∴∠AOB=90°× =54°;∵∠BOF=∠AOF=54°,
∴∠DOF=90°-54°=36°
故答案为:,
【考点】对顶角、邻补角
【解析】【分析】因为∠AOD为直角,所以根据∠AOE和∠AOD的比例关系可求出∠AOE的度数,再利用对顶角相等可知∠BOF的值,进而求出∠DOF的值.
17.【答案】解:设这个角为x, 由题意得,180°﹣x﹣24°=3(90°﹣x),
解得x=57°
【考点】余角和补角
【解析】【分析】设这个角为x,根据余角和补角的概念列出方程,解方程即可.
四、解答题
18.【答案】解:∵a//b,∠1=55°,∠2=40°,
∴∠5=∠1=55°,
∠4=∠2+∠5=95°;
∵∠2+∠3+∠5=180°,
∴∠3=85°.
∴∠3=85°,∠4=95°.
【考点】对顶角、邻补角,平行线的性质
【解析】【分析】如图:由a//b,可得:∠1=∠5,∠4=∠2+∠5(两直线平行,同位角相等);又因为∠2+∠3+∠5=180°,所以可以求得∠3的度数.
19.【答案】解:过点E作EF∥AC,如图所示.
∵EF∥AC,
∴∠AEF=∠CAE=30°,
∵EF∥AC∥BD,
∴∠BEF=∠DBE=45°,
∴∠AEB=∠AEF+∠BEF=75°
【考点】平行线的性质
【解析】【分析】过点E作EF∥AC,由EF∥AC可得出∠AEF=∠CAE,由EF∥BD可得出∠BEF=∠DBE,再根据∠AEB=∠AEF+∠BEF即可得出结论.
五、综合题
20.【答案】(1)75°
(2)360°﹣α﹣β
(3)猜想:∠BED=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β
【考点】平行线的性质
【解析】【解答】解:(1.)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2.)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
【分析】(1)过E作EF∥AB,根据两直线平行,内错角相等进行计算;(2)过E作EF∥AB,根据两直线平行,同旁内角互补进行计算;(3)过点E作EF∥AB,根据两直线平行,内错角相等,以及两直线平行,同旁内角互补进行计算.
21.【答案】(1)同位角:∠FAE和∠B;内错角:∠B和∠DAB;同旁内角:∠EAB和∠B;???
(2)内错角:∠EAC和∠BCA,∠DAC和∠ACG;同旁内角:∠EAC和∠ACG,∠DAC和∠BCA;
(3)内错角:∠BAC和∠ACG,∠FAC和∠BCA;?同旁内角:∠BAC和∠BCA,∠BAC和∠ABC,∠B和∠ACB,∠FAC和∠ACG.
【考点】同位角、内错角、同旁内角
【解析】【解答】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.进行解答.
【分析】此题主要考查了三线八角,关键是掌握同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
22.【答案】(1)解:∠ACE=∠BCD,理由如下: ∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD;
(2)解:若∠DCE=30°,∠ACD=90°, ∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°
(3)解:猜想∠ACB+∠DCE=180°.理由如下: ∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
(4)解:成立.
【考点】余角和补角
【解析】【分析】(1)根据余角的性质,可得答案;(2)根据余角的定义,可得∠ACE,根据角的和差,可得答案;(3)根据角的和差,可得答案;(4)根据角的和差,可得答案.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
