人教版七年级数学下册 9.1.2 不等式的性质 课件(第2课时 共16张PPT)
文档属性
| 名称 | 人教版七年级数学下册 9.1.2 不等式的性质 课件(第2课时 共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 16:28:17 | ||
图片预览






文档简介
(共16张PPT)
9.1.2不等式的性质
第2课时
学习目标
用不等式的性质解不等式
不等式性质的应用
复习巩固
不等式的性质怎么描述?
不等式的性质1:如果a>b,那么a±c>b±c.
不等式的性质2:如果 a>b,c>0,那么ac>bc
不等式的性质3:如果a>b,c<0,那么ac<bc
1、指出下面变形根据的是不等式的哪一条基本性质:
(1)由5a>4,得a>?,根据 ????;
(2)由a+3>0,得a>-3,根据 ???;
(3)由-2a<1,得a>-?,根据 ????;
(4)由3a>2a+1,得a>1,根据 ????.
基础训练9:下列 不等式变形正确的是( )
A.由4x-1>2,得4x>1 B.由5x>3,得x>
C.由 ,得Y>2 D.由-2x<4,得x<-2
B
不等式的性质1
不等式的性质3
不等式的性质1
不等式的性质2
基础训练11:不等式5-2x>1的正整数解是__________。
分析:利用不等式的性质,可得到它的解集为:x<2;所以正整数解就为:x=1。
基础训练12:
已知不等式(a-1)x>b.
(1)如果 ,试求a的取值范围;
(2)如果 ,试求a的取值范围。
x=1
解:
(1)由题意得:a-1>0
∴a>1
(2)由题意得:a-1<0
∴a<1
1
知识点
用不等式的性质解不等式
用数轴表示不等式的解集时要“两定”:
一定边界点,
二定方向;
注意:
若不等号是“≥”或“≤”,则边界点是实心圆点;
若不等号是“>”或“<”,则边界点是空心圆圈.
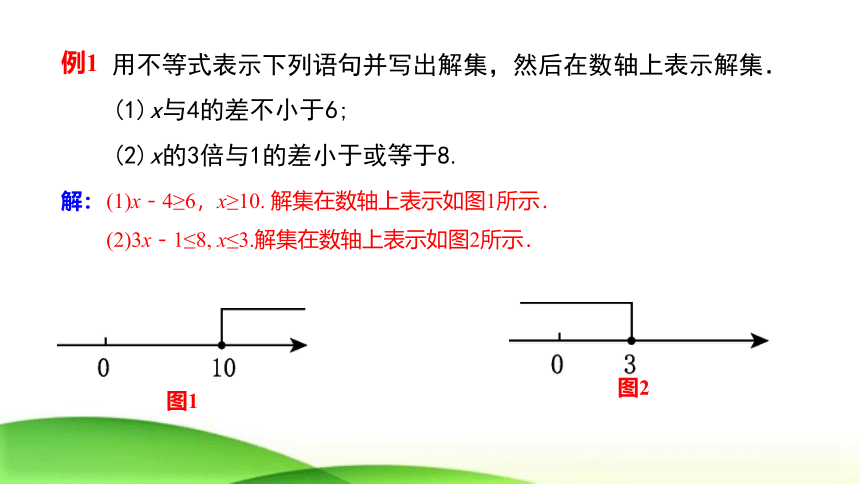
用不等式表示下列语句并写出解集,然后在数轴上表示解集.
(1)x与4的差不小于6;
(2)x的3倍与1的差小于或等于8.
例1
解:
(1)x-4≥6,x≥10. 解集在数轴上表示如图1所示.
(2)3x-1≤8, x≤3.解集在数轴上表示如图2所示.
图1
图2
关键词语 表明数量的不等关系
①大于
②比...大 ①小于
②比...小 ①不大于
②不超过(不足)
③至多 ①不小于
②不低于(高于)
③至少
不等号 > < ≤ ≥
练习:
1、如果式子 有意义,那么x的取值范围在数轴上表示出来,正确的是( )
C
2、满足不等式x-2≤3的自然数是( )
A.1、2、3、4、5 B.0、1、2、3、4、5
C.0、1、2、3、4 D.无数多个
B
2
知识点
不等式性质的应用
某长方体形状的容器长5 cm,宽3 cm, 高10 cm.容器内原有水的高度为3 cm,现准备向它继续注水. 用V(单位:cm3)表示新注入水
的体积,写出V的取值范围 .
例2
10 cm
分析:求新注入水的体积V的取值范围,那就需 要知道容器的体积和原有水的体积。
且:V+原有水的体积不超过容器的体积。
注意:V不能为负数。
解:
由题意可得:
V+3×5×3≤3×5×10,
V≤105.
又∵V不能是负数,
∴V≥0 并且 V≤105.
在数轴上表示V的取值范围如图所示:
练习:
某种品牌的八宝粥,外包装标明:净含量为330±10 g,表明了这罐八宝粥的净含量x的范围是( )
A.320 g<x<340 g
B.320 g≤x<340 g
C.320 g<x≤340 g
D.320 g≤x≤340 g
D
1、C
2、D
3、C
4、B
5、70≤a≤75
总结:
1、用数轴表示不等式解集的一般方法:
①画数轴;
②定边界点,注意边界点是实心还是空心,若边界点在解集内,则是实心圆点,若不在解集内,则是空心圆圈;
③定方向,原则是“小于向左,大于向右”.
用数轴表示不等式的解集,体现了一种重要的数学思想——数形结合思想.
2、列不等式解决实际问题时,要抓住题目中的关键词,利用关键词的意思列出准确的不等式 .
课后作业
基训101页—102页:第6题——第14题
再见!
9.1.2不等式的性质
第2课时
学习目标
用不等式的性质解不等式
不等式性质的应用
复习巩固
不等式的性质怎么描述?
不等式的性质1:如果a>b,那么a±c>b±c.
不等式的性质2:如果 a>b,c>0,那么ac>bc
不等式的性质3:如果a>b,c<0,那么ac<bc
1、指出下面变形根据的是不等式的哪一条基本性质:
(1)由5a>4,得a>?,根据 ????;
(2)由a+3>0,得a>-3,根据 ???;
(3)由-2a<1,得a>-?,根据 ????;
(4)由3a>2a+1,得a>1,根据 ????.
基础训练9:下列 不等式变形正确的是( )
A.由4x-1>2,得4x>1 B.由5x>3,得x>
C.由 ,得Y>2 D.由-2x<4,得x<-2
B
不等式的性质1
不等式的性质3
不等式的性质1
不等式的性质2
基础训练11:不等式5-2x>1的正整数解是__________。
分析:利用不等式的性质,可得到它的解集为:x<2;所以正整数解就为:x=1。
基础训练12:
已知不等式(a-1)x>b.
(1)如果 ,试求a的取值范围;
(2)如果 ,试求a的取值范围。
x=1
解:
(1)由题意得:a-1>0
∴a>1
(2)由题意得:a-1<0
∴a<1
1
知识点
用不等式的性质解不等式
用数轴表示不等式的解集时要“两定”:
一定边界点,
二定方向;
注意:
若不等号是“≥”或“≤”,则边界点是实心圆点;
若不等号是“>”或“<”,则边界点是空心圆圈.
用不等式表示下列语句并写出解集,然后在数轴上表示解集.
(1)x与4的差不小于6;
(2)x的3倍与1的差小于或等于8.
例1
解:
(1)x-4≥6,x≥10. 解集在数轴上表示如图1所示.
(2)3x-1≤8, x≤3.解集在数轴上表示如图2所示.
图1
图2
关键词语 表明数量的不等关系
①大于
②比...大 ①小于
②比...小 ①不大于
②不超过(不足)
③至多 ①不小于
②不低于(高于)
③至少
不等号 > < ≤ ≥
练习:
1、如果式子 有意义,那么x的取值范围在数轴上表示出来,正确的是( )
C
2、满足不等式x-2≤3的自然数是( )
A.1、2、3、4、5 B.0、1、2、3、4、5
C.0、1、2、3、4 D.无数多个
B
2
知识点
不等式性质的应用
某长方体形状的容器长5 cm,宽3 cm, 高10 cm.容器内原有水的高度为3 cm,现准备向它继续注水. 用V(单位:cm3)表示新注入水
的体积,写出V的取值范围 .
例2
10 cm
分析:求新注入水的体积V的取值范围,那就需 要知道容器的体积和原有水的体积。
且:V+原有水的体积不超过容器的体积。
注意:V不能为负数。
解:
由题意可得:
V+3×5×3≤3×5×10,
V≤105.
又∵V不能是负数,
∴V≥0 并且 V≤105.
在数轴上表示V的取值范围如图所示:
练习:
某种品牌的八宝粥,外包装标明:净含量为330±10 g,表明了这罐八宝粥的净含量x的范围是( )
A.320 g<x<340 g
B.320 g≤x<340 g
C.320 g<x≤340 g
D.320 g≤x≤340 g
D
1、C
2、D
3、C
4、B
5、70≤a≤75
总结:
1、用数轴表示不等式解集的一般方法:
①画数轴;
②定边界点,注意边界点是实心还是空心,若边界点在解集内,则是实心圆点,若不在解集内,则是空心圆圈;
③定方向,原则是“小于向左,大于向右”.
用数轴表示不等式的解集,体现了一种重要的数学思想——数形结合思想.
2、列不等式解决实际问题时,要抓住题目中的关键词,利用关键词的意思列出准确的不等式 .
课后作业
基训101页—102页:第6题——第14题
再见!
