五年级下册数学一课一练-4.18长方体的面、棱、顶点 浙教版(含答案)
文档属性
| 名称 | 五年级下册数学一课一练-4.18长方体的面、棱、顶点 浙教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 41.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 17:33:55 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-4.18长方体的面、棱、顶点
一、单选题
1.一个正方体有(? ????)个面。
A.?6个???????????????????????????????????B.?一个???????????????????????????????????C.?6个一样大小的面
2.用一根64厘米长的铁丝,正好可以焊接一个长8厘米、宽4厘米、高( )厘米的框架模型.
A.?2??????????????????????????????????????????????B.?4??????????????????????????????????????????????C.?6
3.两根同样长的铁丝,一根铁丝做成长、宽、高分别是5cm、4cm、3cm的长方体框架(铁丝没有多余),另一根做成最大的正方体框架,这个正方体棱长是(? )厘米。
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
4.要用铁丝围成一个长7厘米、宽5厘米、高2厘米的长方体,至少要用铁丝(? )厘米.
A.?28???????????????????????????????????????????B.?56???????????????????????????????????????????C.?118
二、判断题
5.正方体是特殊的长方体。
6.(1)如果一个长方体有两个面是正方形,那么其余的四个面一定相同。
(2)有6个面,12条棱,8个顶点的立体图形一定是长方体或正方体。
(3)一个正方体的一条棱长是6厘米,这个正方体的所有棱长的和是72厘米。
7.因为正方体的长、宽、高都相等,所以正方体是特殊的长方体。
8.长方体有8个顶点
9.一个长方体如果有四个面是正方形,则这个长方体一定是正方体.
三、填空题
10.把48厘米长的铁丝焊接成一个最大的正方体,这个正方体的棱长是________厘米
11.下列图形中________号是长方体,________号是正方体。
12.挖一个长4米,宽3米,深1.5米的长方体水池,它的占地面积是________平方米,这个水池的容积是________立方米.
13.长方体和正方体都有________个面,________个顶点,________条棱.
四、解答题
14.长方体的长是10分米宽是8分米,高是5分米,长方体的棱长总和是多少分米?
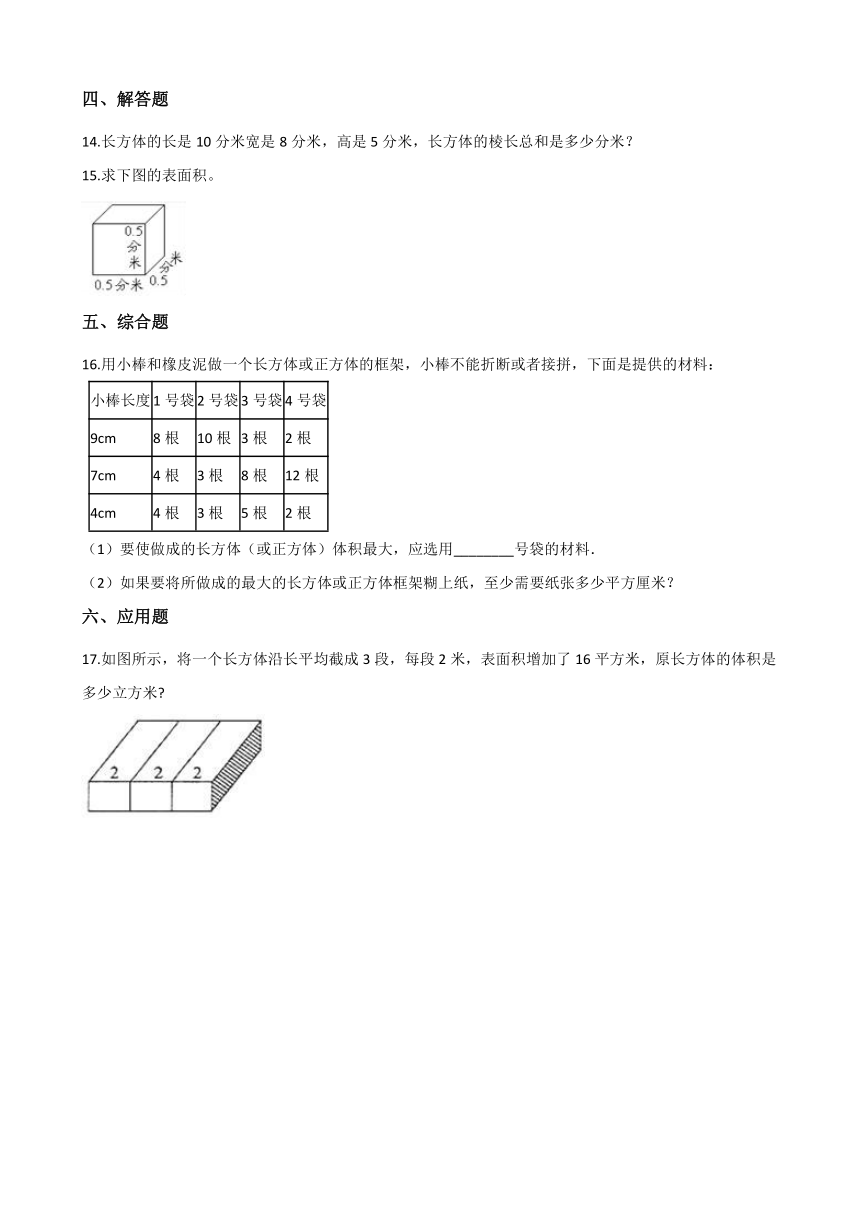
15.求下图的表面积。
五、综合题
16.用小棒和橡皮泥做一个长方体或正方体的框架,小棒不能折断或者接拼,下面是提供的材料:
小棒长度 1号袋 2号袋 3号袋 4号袋
9cm 8根 10根 3根 2根
7cm 4根 3根 8根 12根
4cm 4根 3根 5根 2根
(1)要使做成的长方体(或正方体)体积最大,应选用________号袋的材料.
(2)如果要将所做成的最大的长方体或正方体框架糊上纸,至少需要纸张多少平方厘米?
六、应用题
17.如图所示,将一个长方体沿长平均截成3段,每段2米,表面积增加了16平方米,原长方体的体积是多少立方米?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】一个正方体有6个面。
故选:C
【分析】长方体有6个面,如果每个面都是正方形它就成为正方体,即可得解。
2.【答案】B
【解析】【解答】解:64÷4﹣(8+4)
=16﹣12
=4(厘米),
答:高是4厘米.
故选:B.
【分析】有一根长64厘米的铁丝,恰好可以焊接成一个长方体,这个长方体的棱长总和就是64厘米,长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4减去长与宽的和即可.
3.【答案】 B
【解析】【解答】(5+4+3)×4
=12×4
=48(cm);
48÷12=4(厘米).
故答案为:B.
【分析】已知长方体的长、宽、高,求长方体棱长总和,依据公式:长方体的棱长总和=(长+宽+高)x4,据此求出这根铁丝的长度,然后由公式:正方体的棱长总和=棱长×12,可以推出:正方体的棱长=棱长总和÷12,据此列式解答.
4.【答案】 B
【解析】【解答】解:(7+5+2)×4
=14×4
=56(厘米);
答:至少需要56厘米铁丝.
故选:B.
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可.此题主要考查长方体的棱长总和的计算方法.
二、判断题
5.【答案】正确
【解析】【分析】正方体的概念是:长、宽、高都相等的长方体叫正方体.由此可知正方体是特殊的长方体.答案:正确
6.【答案】(1)1
(2)0
(3)1
【解析】【解答】(1)如果一个长方体有两个面是正方形,那么其余的四个面一定相同,此题说法正确;
(2)长方体或正方体的特征是:有6个面,12条棱,8个顶点,但是有6个面,12条棱,8个顶点的立体图形不一定是长方体或正方体,原题说法错误;
(3)6×12=72(厘米),原题说法正确.
故答案为:(1)正确;(2)错误;(3)正确.
【分析】如果一个长方体有两个面是正方形,那么其余的四个面也是相等的正方形;长方体或正方体的特征是:有6个面,12条棱,8个顶点;已知正方体的棱长,求棱长总和,用公式:正方体的棱长×12=正方体的棱长总和,据此解答.
7.【答案】正确
【解析】【解答】因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,说法正确。
【分析】因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,即可判断。
8.【答案】正确
【解析】【解答】解:根据长方体的特征可知,长方体有8个顶点,原题说法正确.
故答案为:正确
【分析】长方体三条棱长相交的点叫做长方体的顶点,长方体共有8个顶点.
9.【答案】正确
【解析】【解答】解:如果这个长方体有四个面是正方形,那么另外两个面一定是正方形,这个物体一定是正方体.原题说法正确.
故答案为:正确
【分析】长方体最多只有两个相对的面是正方形,正方体每个面都是正方形,由此判断即可.
三、填空题
10.【答案】 4
【解析】【分析】依据正方体的特征,12条棱都相等,求出棱长为48÷12=4答案:4
11.【答案】 ① ;③
【解析】【分析】依据长方体、正方体的特征:长方体有六个面,十二条棱,八个顶点。是由六个长方形(特殊情况下有两个相对面是正方形)围成的立体图形,相对的面完全相同。十二条棱按长度可以分成三组。正方体也有六个面,十二条棱,八个顶点。是由六个正方形围成的立体图形,所有的面完全相同,十二条棱长短完全相同。据此即可判断。所以答案为① 、③
12.【答案】 12;18
【解析】【解答】4×3=12(平方米);12×1.5=18(立方米)。
故答案为:12;18。
【分析】占地面积就是长方体的底面积,占地面积=长×宽,容积=底面积×高。
13.【答案】 6;8;12
【解析】【解答】解:长方体和正方体的共同特征是:长方体和正方体都有6个面,8个顶点,12条棱.
故答案为:6,8,12.
【分析】根据长方体和正方体的共同特征:长方体和正方体都有6个面,8个顶点,12条棱.此题考查的目的是使学生牢固掌握长方体和正方体的共同特征.
四、解答题
14.【答案】解:(10+8+5)×4
=23×4
=92(分米)
答:这个长方体的棱长总和是92分米.
【解析】【分析】长方体的棱长总和=(长+宽+高)×4,据此列式解答.
15.【答案】 解:正方体的表面积=棱长×棱长×6
0.5×0.5×6=1.5(平方分米)
【解析】【分析】先求出一个面的面积,就是正方形的面积,边长乘以边长,因为正方体的6个面,是完全相同的,所以求表面积,只要用一个面的面积乘以6就可以了。
五、综合题
16.【答案】 (1)1
(2)解:表面积为:7×7×2+7×9×4,
=98+252,
=350(平方厘米);
答:如果要将所做成的最大的长方体或正方体框架糊上纸,至少需要纸张350平方厘米
【解析】【解答】解:(1)根据长方体的特征,一般情况长方体的12条棱,分为3组,每组4条棱的长度相等,在特殊情况下,有8条棱的长度相等.
因此,用8根9厘米和4根7厘米长的小棒(不能折断)和橡皮泥,搭成一个正方体,体积最大.
故答案为:1.
【分析】根据长方体的特征,它有12条棱,8个顶点,6个面.它的12条棱分为3组,每组4条棱的长度相等,在特殊情况下(有两个相对的面是正方形),它有8条棱的长度相等,另外4条棱的长度相等,又因长宽高的值越大,其体积就越大,由此确定出长、宽、高的值,再据长方体的表面积即可得解.此题主要考查长方体的棱的特征,由此解决问题.
六、应用题
17.【答案】解:16÷4=4(平方米)
3×2=6(米)
4×6=24(立方米)
答:原长方体的体积是24立方米。
【解析】【分析】表面积增加了16平方米,增加的部分,是4个横截面,那么可以求出每个横截面的面积是4平方米,与原长方体的侧面的面积相同,因为每段2米,原长方形的总长是6米,求出体积是24平方米。
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-4.18长方体的面、棱、顶点
一、单选题
1.一个正方体有(? ????)个面。
A.?6个???????????????????????????????????B.?一个???????????????????????????????????C.?6个一样大小的面
2.用一根64厘米长的铁丝,正好可以焊接一个长8厘米、宽4厘米、高( )厘米的框架模型.
A.?2??????????????????????????????????????????????B.?4??????????????????????????????????????????????C.?6
3.两根同样长的铁丝,一根铁丝做成长、宽、高分别是5cm、4cm、3cm的长方体框架(铁丝没有多余),另一根做成最大的正方体框架,这个正方体棱长是(? )厘米。
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
4.要用铁丝围成一个长7厘米、宽5厘米、高2厘米的长方体,至少要用铁丝(? )厘米.
A.?28???????????????????????????????????????????B.?56???????????????????????????????????????????C.?118
二、判断题
5.正方体是特殊的长方体。
6.(1)如果一个长方体有两个面是正方形,那么其余的四个面一定相同。
(2)有6个面,12条棱,8个顶点的立体图形一定是长方体或正方体。
(3)一个正方体的一条棱长是6厘米,这个正方体的所有棱长的和是72厘米。
7.因为正方体的长、宽、高都相等,所以正方体是特殊的长方体。
8.长方体有8个顶点
9.一个长方体如果有四个面是正方形,则这个长方体一定是正方体.
三、填空题
10.把48厘米长的铁丝焊接成一个最大的正方体,这个正方体的棱长是________厘米
11.下列图形中________号是长方体,________号是正方体。
12.挖一个长4米,宽3米,深1.5米的长方体水池,它的占地面积是________平方米,这个水池的容积是________立方米.
13.长方体和正方体都有________个面,________个顶点,________条棱.
四、解答题
14.长方体的长是10分米宽是8分米,高是5分米,长方体的棱长总和是多少分米?
15.求下图的表面积。
五、综合题
16.用小棒和橡皮泥做一个长方体或正方体的框架,小棒不能折断或者接拼,下面是提供的材料:
小棒长度 1号袋 2号袋 3号袋 4号袋
9cm 8根 10根 3根 2根
7cm 4根 3根 8根 12根
4cm 4根 3根 5根 2根
(1)要使做成的长方体(或正方体)体积最大,应选用________号袋的材料.
(2)如果要将所做成的最大的长方体或正方体框架糊上纸,至少需要纸张多少平方厘米?
六、应用题
17.如图所示,将一个长方体沿长平均截成3段,每段2米,表面积增加了16平方米,原长方体的体积是多少立方米?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】一个正方体有6个面。
故选:C
【分析】长方体有6个面,如果每个面都是正方形它就成为正方体,即可得解。
2.【答案】B
【解析】【解答】解:64÷4﹣(8+4)
=16﹣12
=4(厘米),
答:高是4厘米.
故选:B.
【分析】有一根长64厘米的铁丝,恰好可以焊接成一个长方体,这个长方体的棱长总和就是64厘米,长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4减去长与宽的和即可.
3.【答案】 B
【解析】【解答】(5+4+3)×4
=12×4
=48(cm);
48÷12=4(厘米).
故答案为:B.
【分析】已知长方体的长、宽、高,求长方体棱长总和,依据公式:长方体的棱长总和=(长+宽+高)x4,据此求出这根铁丝的长度,然后由公式:正方体的棱长总和=棱长×12,可以推出:正方体的棱长=棱长总和÷12,据此列式解答.
4.【答案】 B
【解析】【解答】解:(7+5+2)×4
=14×4
=56(厘米);
答:至少需要56厘米铁丝.
故选:B.
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可.此题主要考查长方体的棱长总和的计算方法.
二、判断题
5.【答案】正确
【解析】【分析】正方体的概念是:长、宽、高都相等的长方体叫正方体.由此可知正方体是特殊的长方体.答案:正确
6.【答案】(1)1
(2)0
(3)1
【解析】【解答】(1)如果一个长方体有两个面是正方形,那么其余的四个面一定相同,此题说法正确;
(2)长方体或正方体的特征是:有6个面,12条棱,8个顶点,但是有6个面,12条棱,8个顶点的立体图形不一定是长方体或正方体,原题说法错误;
(3)6×12=72(厘米),原题说法正确.
故答案为:(1)正确;(2)错误;(3)正确.
【分析】如果一个长方体有两个面是正方形,那么其余的四个面也是相等的正方形;长方体或正方体的特征是:有6个面,12条棱,8个顶点;已知正方体的棱长,求棱长总和,用公式:正方体的棱长×12=正方体的棱长总和,据此解答.
7.【答案】正确
【解析】【解答】因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,说法正确。
【分析】因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,即可判断。
8.【答案】正确
【解析】【解答】解:根据长方体的特征可知,长方体有8个顶点,原题说法正确.
故答案为:正确
【分析】长方体三条棱长相交的点叫做长方体的顶点,长方体共有8个顶点.
9.【答案】正确
【解析】【解答】解:如果这个长方体有四个面是正方形,那么另外两个面一定是正方形,这个物体一定是正方体.原题说法正确.
故答案为:正确
【分析】长方体最多只有两个相对的面是正方形,正方体每个面都是正方形,由此判断即可.
三、填空题
10.【答案】 4
【解析】【分析】依据正方体的特征,12条棱都相等,求出棱长为48÷12=4答案:4
11.【答案】 ① ;③
【解析】【分析】依据长方体、正方体的特征:长方体有六个面,十二条棱,八个顶点。是由六个长方形(特殊情况下有两个相对面是正方形)围成的立体图形,相对的面完全相同。十二条棱按长度可以分成三组。正方体也有六个面,十二条棱,八个顶点。是由六个正方形围成的立体图形,所有的面完全相同,十二条棱长短完全相同。据此即可判断。所以答案为① 、③
12.【答案】 12;18
【解析】【解答】4×3=12(平方米);12×1.5=18(立方米)。
故答案为:12;18。
【分析】占地面积就是长方体的底面积,占地面积=长×宽,容积=底面积×高。
13.【答案】 6;8;12
【解析】【解答】解:长方体和正方体的共同特征是:长方体和正方体都有6个面,8个顶点,12条棱.
故答案为:6,8,12.
【分析】根据长方体和正方体的共同特征:长方体和正方体都有6个面,8个顶点,12条棱.此题考查的目的是使学生牢固掌握长方体和正方体的共同特征.
四、解答题
14.【答案】解:(10+8+5)×4
=23×4
=92(分米)
答:这个长方体的棱长总和是92分米.
【解析】【分析】长方体的棱长总和=(长+宽+高)×4,据此列式解答.
15.【答案】 解:正方体的表面积=棱长×棱长×6
0.5×0.5×6=1.5(平方分米)
【解析】【分析】先求出一个面的面积,就是正方形的面积,边长乘以边长,因为正方体的6个面,是完全相同的,所以求表面积,只要用一个面的面积乘以6就可以了。
五、综合题
16.【答案】 (1)1
(2)解:表面积为:7×7×2+7×9×4,
=98+252,
=350(平方厘米);
答:如果要将所做成的最大的长方体或正方体框架糊上纸,至少需要纸张350平方厘米
【解析】【解答】解:(1)根据长方体的特征,一般情况长方体的12条棱,分为3组,每组4条棱的长度相等,在特殊情况下,有8条棱的长度相等.
因此,用8根9厘米和4根7厘米长的小棒(不能折断)和橡皮泥,搭成一个正方体,体积最大.
故答案为:1.
【分析】根据长方体的特征,它有12条棱,8个顶点,6个面.它的12条棱分为3组,每组4条棱的长度相等,在特殊情况下(有两个相对的面是正方形),它有8条棱的长度相等,另外4条棱的长度相等,又因长宽高的值越大,其体积就越大,由此确定出长、宽、高的值,再据长方体的表面积即可得解.此题主要考查长方体的棱的特征,由此解决问题.
六、应用题
17.【答案】解:16÷4=4(平方米)
3×2=6(米)
4×6=24(立方米)
答:原长方体的体积是24立方米。
【解析】【分析】表面积增加了16平方米,增加的部分,是4个横截面,那么可以求出每个横截面的面积是4平方米,与原长方体的侧面的面积相同,因为每段2米,原长方形的总长是6米,求出体积是24平方米。
