15.5 三角形中位线定理 课件(15张PPT)
文档属性
| 名称 | 15.5 三角形中位线定理 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览


文档简介
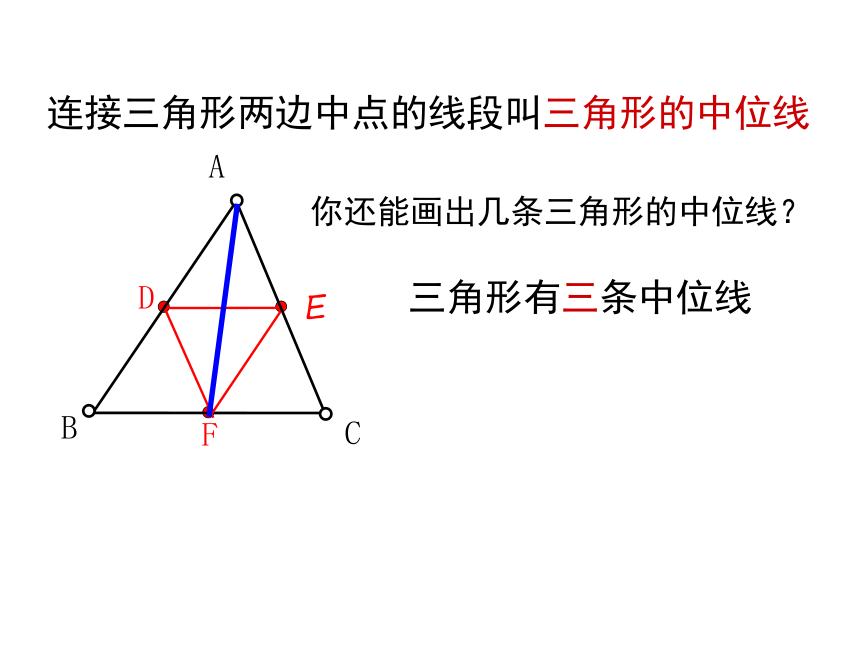
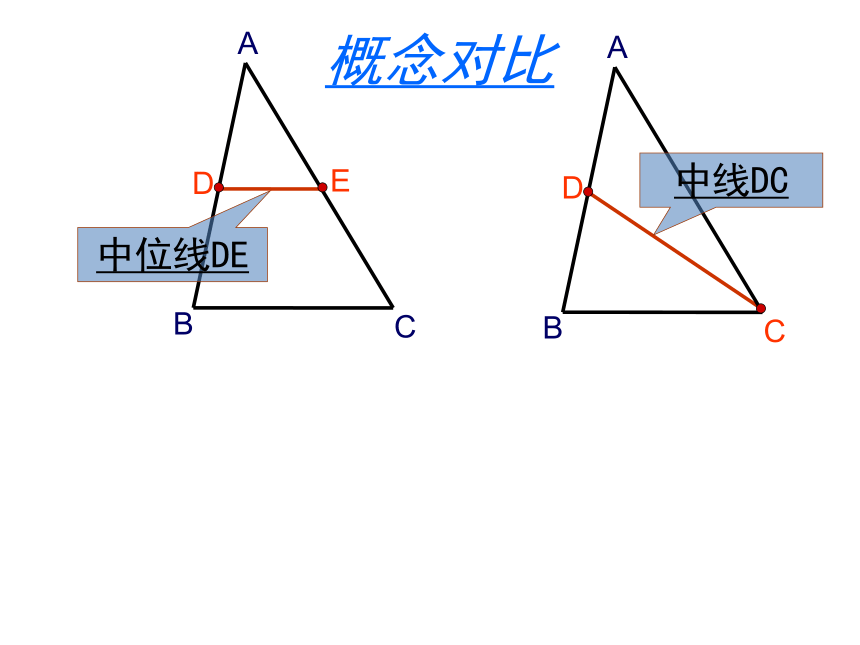
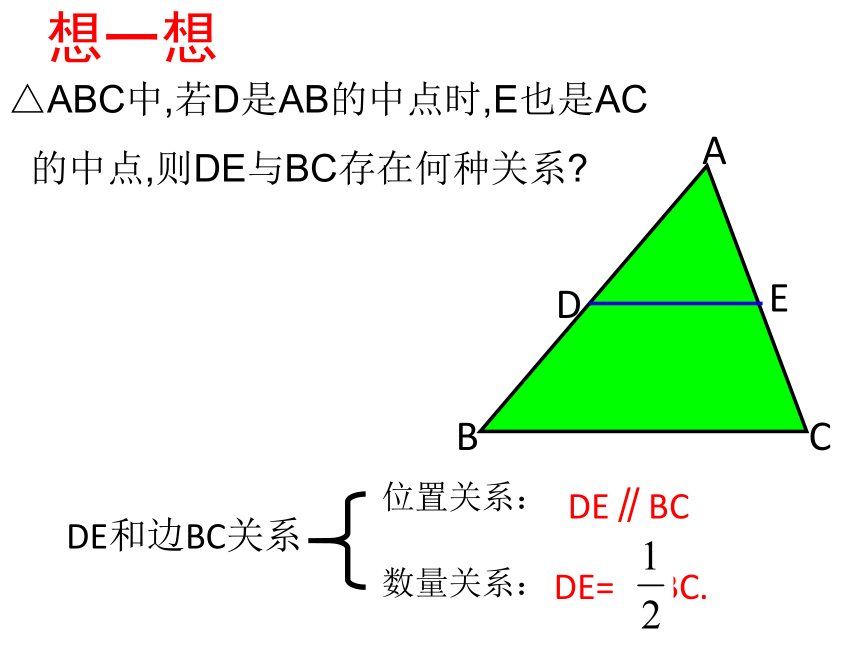
课件15张PPT。 如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。创设情境,导入新课三角形的中位线连接三角形两边中点的线段叫三角形的中位线三角形有三条中位线EDF你还能画出几条三角形的中位线?概念对比中线DC中位线DEDE和边BC关系数量关系:位置关系:△ABC中,若D是AB的中点时,E也是AC
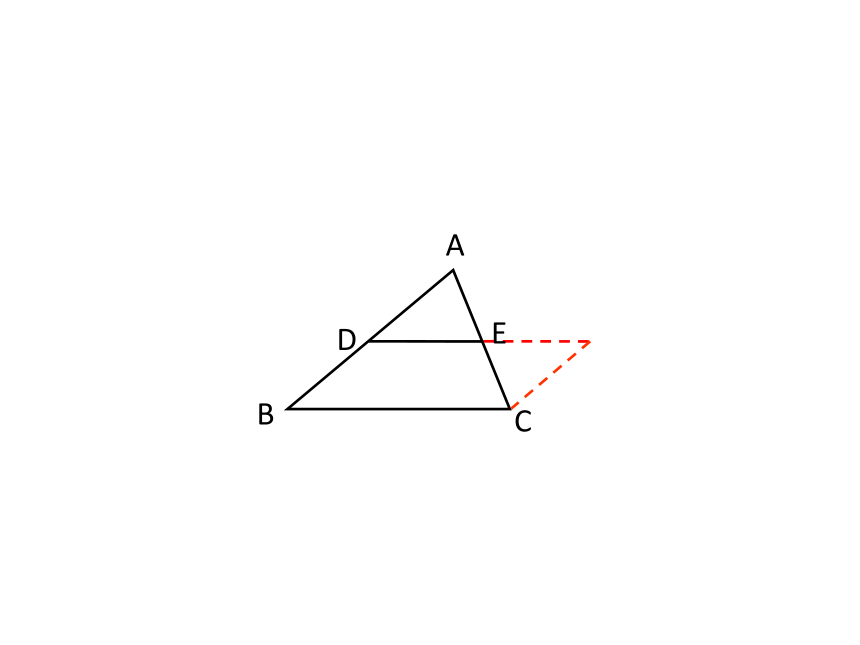
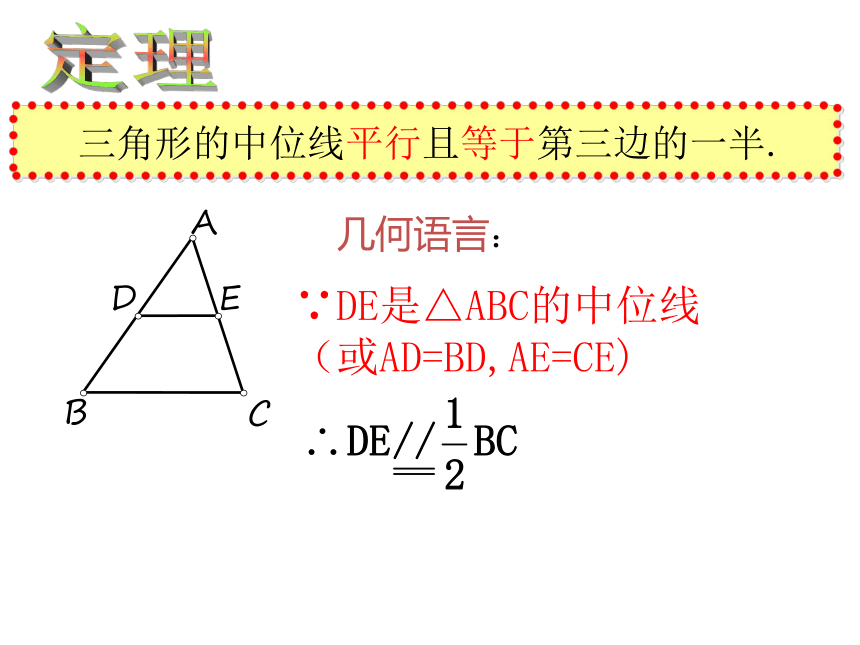
的中点,则DE与BC存在何种关系?想一想ABCDE定理 三角形的中位线平行且等于第三边的一半.几何语言:∵DE是△ABC的中位线(或AD=BD,AE=CE)EDF如图,在△ABC中,D、E分别是AB、AC的中点(3)若△ABC的面积为24,
△DEF的面积是___(1)图中有_____个平行四边形(2)若△ABC的周长为24,△DEF的周长是___1、 三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?探究活动2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系? 例1 求证三角形的一条中位线与第三边上的中线
互相平分.已知:△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE与DF互相平分.E证明:连接DE、EF,因为
AD=DB,BE=EC,
所以DE ∥AC(三角形的中位线平行于第三边并且等于第三边的一半)。
同理EF ∥AB。
所以四边形ADEF是平行四边形。
因此AE、DF互相平分。(平行四边形的对角线互相平分)例2. 如图,在四边形ABCD中,E、F、G、
H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. 例3.已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证∠1=∠2. 1.如图,在△ABC中, BC>AC,点D在BC边上,且DC=AC, ∠ACB的平分线CF交AD于F ,点E是AB的中点,连接EF,求证:EF是△ABD的中位线.初显身手课外拓展说一说你学到了什么?
的中点,则DE与BC存在何种关系?想一想ABCDE定理 三角形的中位线平行且等于第三边的一半.几何语言:∵DE是△ABC的中位线(或AD=BD,AE=CE)EDF如图,在△ABC中,D、E分别是AB、AC的中点(3)若△ABC的面积为24,
△DEF的面积是___(1)图中有_____个平行四边形(2)若△ABC的周长为24,△DEF的周长是___1、 三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?探究活动2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系? 例1 求证三角形的一条中位线与第三边上的中线
互相平分.已知:△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE与DF互相平分.E证明:连接DE、EF,因为
AD=DB,BE=EC,
所以DE ∥AC(三角形的中位线平行于第三边并且等于第三边的一半)。
同理EF ∥AB。
所以四边形ADEF是平行四边形。
因此AE、DF互相平分。(平行四边形的对角线互相平分)例2. 如图,在四边形ABCD中,E、F、G、
H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. 例3.已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证∠1=∠2. 1.如图,在△ABC中, BC>AC,点D在BC边上,且DC=AC, ∠ACB的平分线CF交AD于F ,点E是AB的中点,连接EF,求证:EF是△ABD的中位线.初显身手课外拓展说一说你学到了什么?
同课章节目录
