15.5 三角形中位线定理 课件(17张)
文档属性
| 名称 | 15.5 三角形中位线定理 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览



文档简介
课件17张PPT。15.5 三角形的中位线定理复习引入 1、平行四边形有哪些性质?对边相等,对边平行 2、平行四边形有哪些判定方法?对角相等,邻角互补对角线互相平分两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
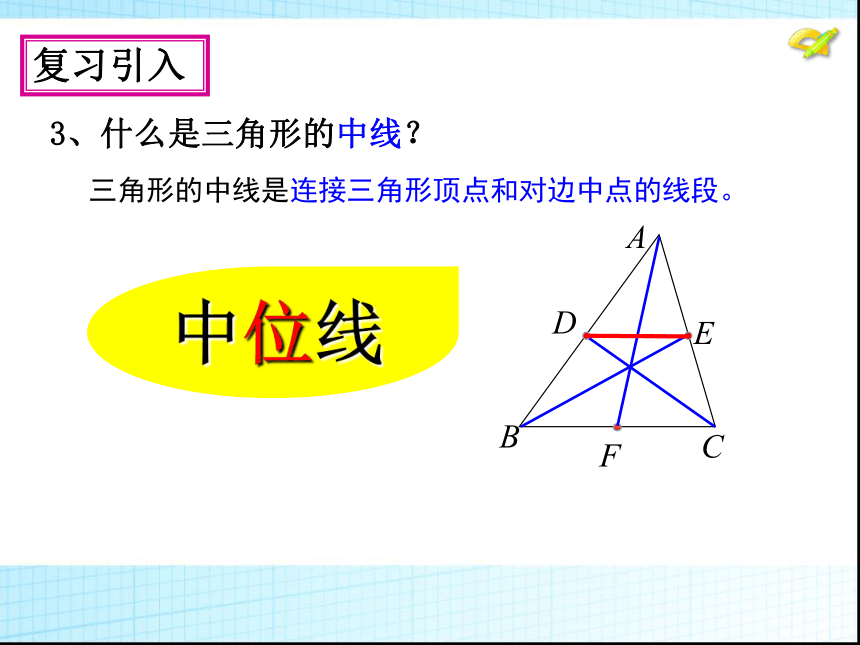
一组对边平行且相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形复习引入 3、什么是三角形的中线?三角形的中线是连接三角形顶点和对边中点的线段。F E D 中位线 如图,△ABC中,D,E分别是边AB,AC 的中点,连接DE. 概念理解 A B CE 一个三角形有三条中位线。问题1:一个三角形有几条中位线?D F问题2:三角形的中位线与中线有什么区别? 端点不一样像DE这样,连接三角形两边中点的线段叫做三角形的中位线.问题3:三角形的中位线与三角形的第三边有什么关系?1、用量角器度量∠ADE和∠ABC,它们有怎样的关系?由此可 以推断出DE和BC之间有什么位置关系?观察度量,提出猜想 2、用刻度尺度量线段DE和BC,它们之间又有怎么的数量关系?探究:
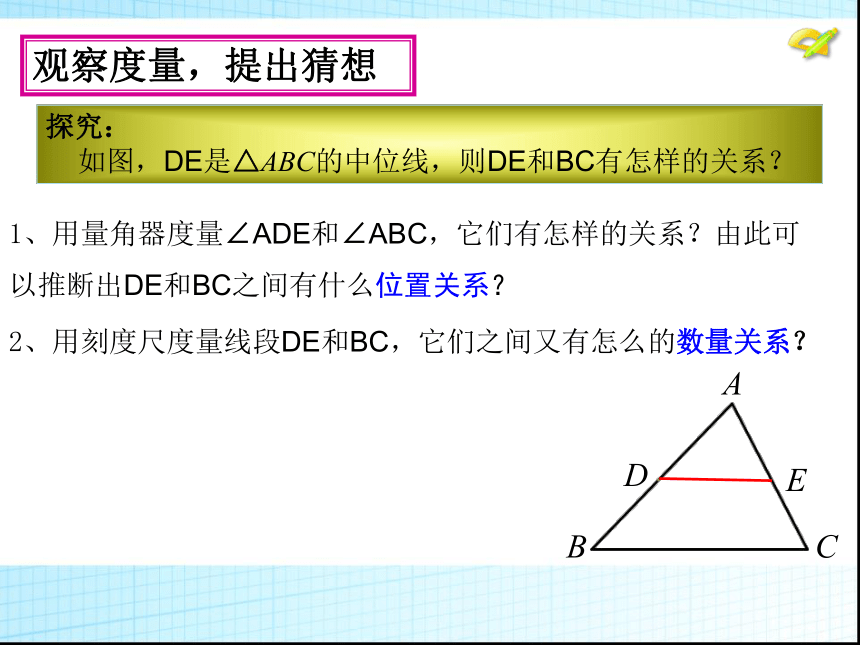
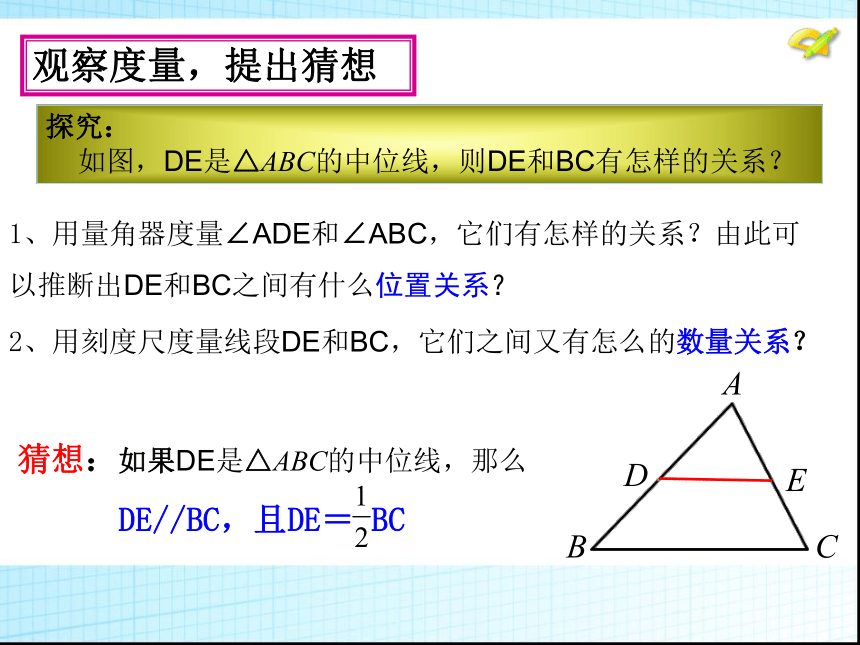
如图,DE是△ABC的中位线,则DE和BC有怎样的关系?1、用量角器度量∠ADE和∠ABC,它们有怎样的关系?由此可 以推断出DE和BC之间有什么位置关系?观察度量,提出猜想 2、用刻度尺度量线段DE和BC,它们之间又有怎么的数量关系?探究:
如图,DE是△ABC的中位线,则DE和BC有怎样的关系?证明猜想 拼图游戏 把一个三角形沿中位线剪开,能否拼成一个平行四边形?怎么拼?请大家一起动手拼一拼。三角形问题平行四边形问题转化证明猜想 已知:如图,D、E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,且DE= BC.F证明:延长DE到点F,使EF=DE,连接CF.∵AE=CE,∠AED=∠CEF
∴△ADE≌△CFE(SAS)∴AD=CF,∠ADE=∠F∴AD∥CF,即 BD∥CF又∵AD=BD
∴BD=CF∴四边形BCFD是平行四边形∴DF∥BC,DF=BC证明猜想 已知:如图,D、E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,且DE= BC.F证明:延长DE到点F,使EF=DE,
连接CF、CD、AF. ∵AE=EC,DE=EF
∴四边形ADCF是平行四边形 ∴四边形DBCF是平行四边形 三角形中位线定理:三角形的中位线平行于三角形
的第三边,并且等于第三边的一半.得出结论 通过以上证明,我们得到了三角形的中位线定理:符号语言: 例1. 如图,△ABC中,D、E分别是AB、AC中点.(1) 若DE=5,则BC= .(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .1065x2xx+2x=12x=48应用示例 巩固练习 1、如图,要测量A、B两点间距离,在O点打桩,取OA的中点 C,OB的中点D,测得CD=30米,则AB= 米。602.已知三角形的各边长分别为6cm,8cm,12cm,那么连结各边中点所成三角形的周长是_________。13 cm306812346(1)本节课我们学习了哪些知识?课堂小结 观察度量--提出猜想--证明猜想--得出结论 三角形的中位线:连结三角形两边中点的线段。
三角形的中位线定理:连接三角形两边中点的线段平行于第三边,且等于第三边的一半.(2)我们是怎么探究三角形的中位线定理的?作业:
课本49页 练习 第1,2,3题
同步练习布置作业 谢谢!
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形复习引入 3、什么是三角形的中线?三角形的中线是连接三角形顶点和对边中点的线段。F E D 中位线 如图,△ABC中,D,E分别是边AB,AC 的中点,连接DE. 概念理解 A B CE 一个三角形有三条中位线。问题1:一个三角形有几条中位线?D F问题2:三角形的中位线与中线有什么区别? 端点不一样像DE这样,连接三角形两边中点的线段叫做三角形的中位线.问题3:三角形的中位线与三角形的第三边有什么关系?1、用量角器度量∠ADE和∠ABC,它们有怎样的关系?由此可 以推断出DE和BC之间有什么位置关系?观察度量,提出猜想 2、用刻度尺度量线段DE和BC,它们之间又有怎么的数量关系?探究:
如图,DE是△ABC的中位线,则DE和BC有怎样的关系?1、用量角器度量∠ADE和∠ABC,它们有怎样的关系?由此可 以推断出DE和BC之间有什么位置关系?观察度量,提出猜想 2、用刻度尺度量线段DE和BC,它们之间又有怎么的数量关系?探究:
如图,DE是△ABC的中位线,则DE和BC有怎样的关系?证明猜想 拼图游戏 把一个三角形沿中位线剪开,能否拼成一个平行四边形?怎么拼?请大家一起动手拼一拼。三角形问题平行四边形问题转化证明猜想 已知:如图,D、E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,且DE= BC.F证明:延长DE到点F,使EF=DE,连接CF.∵AE=CE,∠AED=∠CEF
∴△ADE≌△CFE(SAS)∴AD=CF,∠ADE=∠F∴AD∥CF,即 BD∥CF又∵AD=BD
∴BD=CF∴四边形BCFD是平行四边形∴DF∥BC,DF=BC证明猜想 已知:如图,D、E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,且DE= BC.F证明:延长DE到点F,使EF=DE,
连接CF、CD、AF. ∵AE=EC,DE=EF
∴四边形ADCF是平行四边形 ∴四边形DBCF是平行四边形 三角形中位线定理:三角形的中位线平行于三角形
的第三边,并且等于第三边的一半.得出结论 通过以上证明,我们得到了三角形的中位线定理:符号语言: 例1. 如图,△ABC中,D、E分别是AB、AC中点.(1) 若DE=5,则BC= .(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .1065x2xx+2x=12x=48应用示例 巩固练习 1、如图,要测量A、B两点间距离,在O点打桩,取OA的中点 C,OB的中点D,测得CD=30米,则AB= 米。602.已知三角形的各边长分别为6cm,8cm,12cm,那么连结各边中点所成三角形的周长是_________。13 cm306812346(1)本节课我们学习了哪些知识?课堂小结 观察度量--提出猜想--证明猜想--得出结论 三角形的中位线:连结三角形两边中点的线段。
三角形的中位线定理:连接三角形两边中点的线段平行于第三边,且等于第三边的一半.(2)我们是怎么探究三角形的中位线定理的?作业:
课本49页 练习 第1,2,3题
同步练习布置作业 谢谢!
同课章节目录
