15.5 三角形中位线定理 课件(29张PPT)
文档属性
| 名称 | 15.5 三角形中位线定理 课件(29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 970.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 15:07:16 | ||
图片预览







文档简介
课件29张PPT。三角形的中位线1、了解三角形中位线的概念。
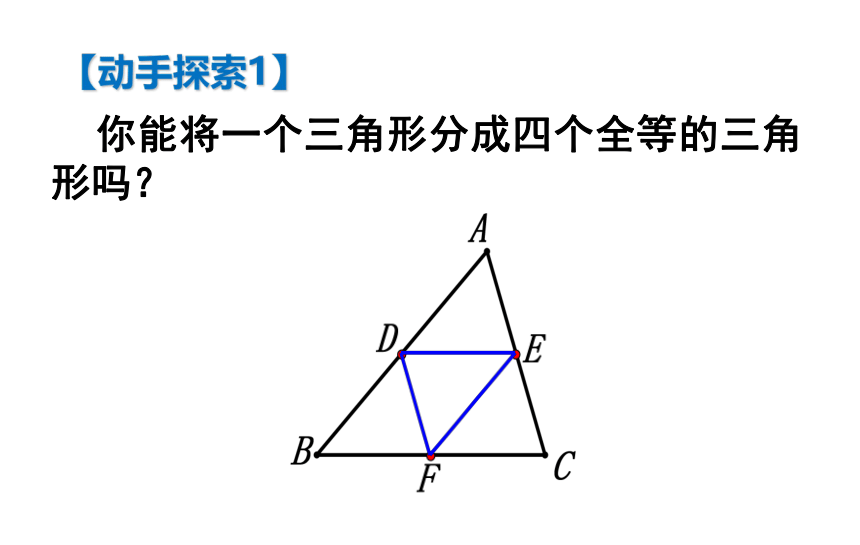
2、探索并掌握三角形中位线的性质,并能应用其性质解决有关问题。【学习目标】 你能将一个三角形分成四个全等的三角形吗?【动手探索1】 连接三角形两边中点的线段叫做三角形的中位线.【定义】∵AD=BD ,AE=EC
∴ DE是△ABC的中位线∵DE是△ABC的中位线
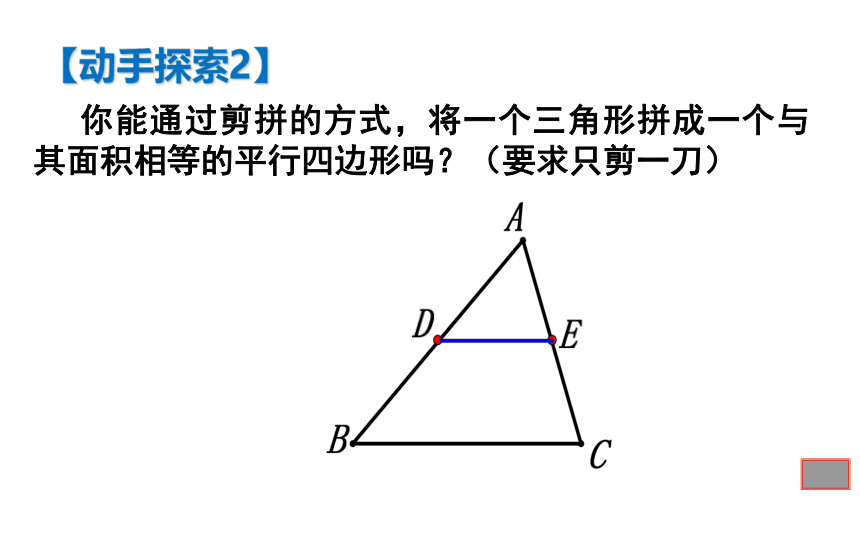
∴ AD=BD ,AE=EC 三角形的中位线与三角形的中线有什么区别与联系? 中位线的两个端点是两边的中点,而中线的两个端点是一个顶点和对边的中点.【定义辨析】 你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?(要求只剪一刀)【动手探索2】【提出猜想】 三角形的中位线平行于第三边,且等于第三边的一半.如何证明?你能证明吗?【证明猜想】∴四边形BCFD是平行四边形∴△ADE ≌△CFE(SAS)证明:如图,延长DE到 F,使EF=DE,连接 CF.∴AD=FC,∠A=∠ECF
∴BD∥FC∴DF∥BC,DF=BC,在△ADE和△CFE中:∴DE∥BC,∵AD=BD,∴BD=CF. 三角形的中位线平行于第三边,且等于第三边的一半.【三角形中位线定理】用符号语言表示【定理的理解】(1)从条件看,以后我们看到中点,尤其是两个或者两个以上的中点时我们就要联想到三角形的中位线定理. (2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),大家以后在解决相关问题时要两方面结合起来灵活应用. 三角形的中位线平行于第三边,并且等于第三边的一半.己知:D、E分别为AB、AC的中点.
(1)∵ D、E分别为AB、AC的中点.
∴ DE∥BC(根据? ???? )
(2)若BC =10cm,则DE = ㎝.
(3)若DE =6cm,则BC = cm.
(4)若∠ADE=60°,则∠B= 度三角形中位线定理512【应用新知1】60【应用新知2】如图,DE为△ABC的中位线,AF为BC边上的中线。
求证:DE和AF互相平分。F 已知:D、E、F分别为△ABC三边的中点,你能证明图中的四个小三角形全等吗?【应用新知3】①③④②(2)四边形ADFE、四边形BDEF、四边形CEDF均为平行四边形;【图形再探】(1)△ADE≌△DBF≌△EFC≌△FED 【拓展探究】顺次连接任意四边形ABCD的四条边的中点E、F、G、H,所得的四边形EFGH会是特殊四边形吗? 证明:连接AC,
∵ AE=EB、CF=FB,
∴EF∥HG,且EF=HG
∴四边形EFGH是平行四边形.分享收获1.探究猜想证明应用3.联想转化2.三角形的中位线定理定义 【拓展探究2】 聪明的小明先在AB外选一点C,然后测出AC,BC的中点D,E,并测出DE的长,由此他就知道了A,B间的距离,你能说出其中的道理吗?
1.大册对应课时如何应用三角形的中位线定理解决问题?怎 样能更好地应用?【作业布置】梯形中位线的定义:连接梯形两腰中点的线段叫做梯形的中位线。2. 课后探究证明:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC,又DB=AD,
∴DB // FC,DB =FC,
∴四边形BCFD是平行四边形
∴DE//BC且DE=EF=1/2BC证明:如图,延长DE至F, 使EF=DE,连接CD、AF、CF
∵AE=EC ,∴DE=EF
∴四边形ADCF是平行四边形
∴AD//FC,AD=FC
又D为AB中点,
∴DB//FC,DB=FC
∴四边形BCFD是平行四边形?
∴DE// BC 且DE=EF=1/2BC如图,取BC的中点F,连接FE并延长,使得EG=FE,连接AG.
∵ AE=EC, ∠AEG=∠CEF, EF=EG,
∴△AEG≌△CEF,
∴AG=FC,∠G=∠EFC,∴AG∥FC,AG=FC
又∵F为BC中点,
∴AG∥FB,AG=FB,
∴四边形ABFG是平行四边形, ∴AB∥GF,AB=GF
又∵D为AB中点,E为GF中点,∴DB∥ EF, DB= EF,
∴四边形DBFE是平行四边形, ∴DE∥BF,即DE∥BC,DE=BF=FC即DE=1/2BC.证明(面积法):连接CD、BE,作DG⊥BC于点G
作EH⊥BC 于点H,
∵点D、E为线段AB、AC的中点,
∴S△BCE=S△BCD=(1/2)S△ABC,
S△CDE=(1/2)S△BCE
∴DE∥BC,DE=(1/2)BC证明(坐标法):建立如图所示的坐标系,
设B (0,0),C (c,0), A (a,b),∵D、E分别AB、AC的中点,
2、探索并掌握三角形中位线的性质,并能应用其性质解决有关问题。【学习目标】 你能将一个三角形分成四个全等的三角形吗?【动手探索1】 连接三角形两边中点的线段叫做三角形的中位线.【定义】∵AD=BD ,AE=EC
∴ DE是△ABC的中位线∵DE是△ABC的中位线
∴ AD=BD ,AE=EC 三角形的中位线与三角形的中线有什么区别与联系? 中位线的两个端点是两边的中点,而中线的两个端点是一个顶点和对边的中点.【定义辨析】 你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?(要求只剪一刀)【动手探索2】【提出猜想】 三角形的中位线平行于第三边,且等于第三边的一半.如何证明?你能证明吗?【证明猜想】∴四边形BCFD是平行四边形∴△ADE ≌△CFE(SAS)证明:如图,延长DE到 F,使EF=DE,连接 CF.∴AD=FC,∠A=∠ECF
∴BD∥FC∴DF∥BC,DF=BC,在△ADE和△CFE中:∴DE∥BC,∵AD=BD,∴BD=CF. 三角形的中位线平行于第三边,且等于第三边的一半.【三角形中位线定理】用符号语言表示【定理的理解】(1)从条件看,以后我们看到中点,尤其是两个或者两个以上的中点时我们就要联想到三角形的中位线定理. (2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),大家以后在解决相关问题时要两方面结合起来灵活应用. 三角形的中位线平行于第三边,并且等于第三边的一半.己知:D、E分别为AB、AC的中点.
(1)∵ D、E分别为AB、AC的中点.
∴ DE∥BC(根据? ???? )
(2)若BC =10cm,则DE = ㎝.
(3)若DE =6cm,则BC = cm.
(4)若∠ADE=60°,则∠B= 度三角形中位线定理512【应用新知1】60【应用新知2】如图,DE为△ABC的中位线,AF为BC边上的中线。
求证:DE和AF互相平分。F 已知:D、E、F分别为△ABC三边的中点,你能证明图中的四个小三角形全等吗?【应用新知3】①③④②(2)四边形ADFE、四边形BDEF、四边形CEDF均为平行四边形;【图形再探】(1)△ADE≌△DBF≌△EFC≌△FED 【拓展探究】顺次连接任意四边形ABCD的四条边的中点E、F、G、H,所得的四边形EFGH会是特殊四边形吗? 证明:连接AC,
∵ AE=EB、CF=FB,
∴EF∥HG,且EF=HG
∴四边形EFGH是平行四边形.分享收获1.探究猜想证明应用3.联想转化2.三角形的中位线定理定义 【拓展探究2】 聪明的小明先在AB外选一点C,然后测出AC,BC的中点D,E,并测出DE的长,由此他就知道了A,B间的距离,你能说出其中的道理吗?
1.大册对应课时如何应用三角形的中位线定理解决问题?怎 样能更好地应用?【作业布置】梯形中位线的定义:连接梯形两腰中点的线段叫做梯形的中位线。2. 课后探究证明:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC,又DB=AD,
∴DB // FC,DB =FC,
∴四边形BCFD是平行四边形
∴DE//BC且DE=EF=1/2BC证明:如图,延长DE至F, 使EF=DE,连接CD、AF、CF
∵AE=EC ,∴DE=EF
∴四边形ADCF是平行四边形
∴AD//FC,AD=FC
又D为AB中点,
∴DB//FC,DB=FC
∴四边形BCFD是平行四边形?
∴DE// BC 且DE=EF=1/2BC如图,取BC的中点F,连接FE并延长,使得EG=FE,连接AG.
∵ AE=EC, ∠AEG=∠CEF, EF=EG,
∴△AEG≌△CEF,
∴AG=FC,∠G=∠EFC,∴AG∥FC,AG=FC
又∵F为BC中点,
∴AG∥FB,AG=FB,
∴四边形ABFG是平行四边形, ∴AB∥GF,AB=GF
又∵D为AB中点,E为GF中点,∴DB∥ EF, DB= EF,
∴四边形DBFE是平行四边形, ∴DE∥BF,即DE∥BC,DE=BF=FC即DE=1/2BC.证明(面积法):连接CD、BE,作DG⊥BC于点G
作EH⊥BC 于点H,
∵点D、E为线段AB、AC的中点,
∴S△BCE=S△BCD=(1/2)S△ABC,
S△CDE=(1/2)S△BCE
∴DE∥BC,DE=(1/2)BC证明(坐标法):建立如图所示的坐标系,
设B (0,0),C (c,0), A (a,b),∵D、E分别AB、AC的中点,
同课章节目录
