人教版数学七年级下册 7.2.2 用坐标表示平移 课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册 7.2.2 用坐标表示平移 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 512.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
7.2.2用坐标表示平移
B
A
C
A′.
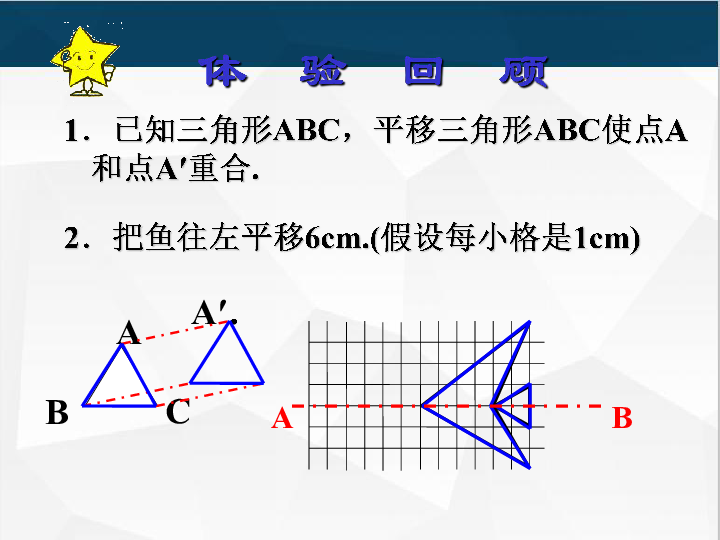
1.已知三角形ABC,平移三角形ABC使点A和点A′重合.
2.把鱼往左平移6cm.(假设每小格是1cm)
A
B
体 验 回 顾
1. 什么叫做平移?
2 . 平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移.
平移后图形的位置改变,形状、大小不变.
7.2.2用坐标表示平移
^
y
>
x
0
1
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
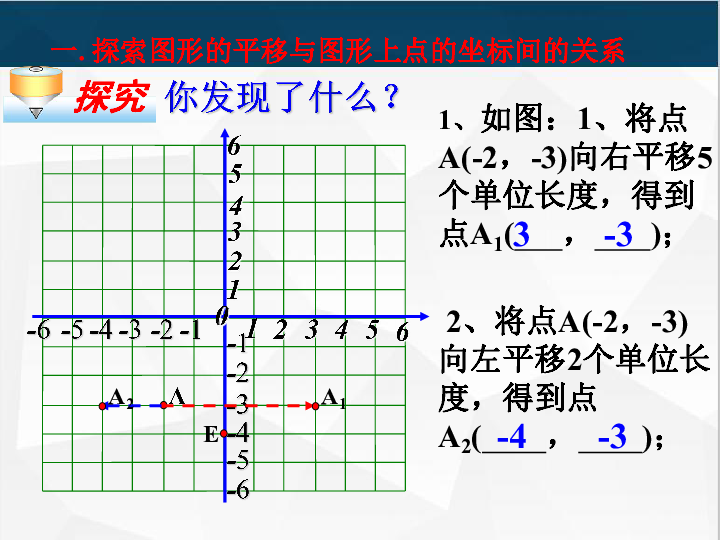
1、如图:1、将点A(-2,-3)向右平移5个单位长度,得到点A1( , );
2、将点A(-2,-3)向左平移2个单位长度,得到点A2( , );
A1
-4
-3
3
-3
A2
你发现了什么?
一. 探索图形的平移与图形上点的坐标间的关系
探究
(1)左、右平移:
向右平移a个单位
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
总结规律1:
图形平移与点的坐标变化间的关系
左右平移:左减右加纵不变
探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
3、将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4、将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
你发现了什么?
一. 探索图形的平移与图形上点的坐标间的关系
(2)上、下平移:
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
总结规律2:
图形平移与点的坐标变化间的关系
上下平移:上加下减横不变
我来试一试
1.已知点A(-2,-3):
(1)将点A向右平移5个单位长度得到点A1,则 点A1点
的坐标是 ;
(2)将点A向左平移6个单位长度得到点A2,则 点A2点
的坐标是 ;
(3,-3)
(-8,-3)
右加纵不变
左减纵不变
(3)将点A向上平移3个单位长度得到点A1,则 点A1点
的坐标是 ;
(4)将点A向下平移4个单位长度得到点A2,则 点A2点
的坐标是 ;
上加横不变
下减横不变
左右平移:左减右加纵不变
上下平移:上加下减横不变
(-2,0)
(-2,-7)
2. 将坐标为(-4,-1)的点向右平移2个单位长度,再向上平移3个单位长度,则平移后的点的坐标分别是( )
A.(2,2)
B.(-2,2)
C.(-2,-2)
D.(2,-2)
C
右移横加
上移纵加
如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
课本78页练习
练习:
A′
B′
C′
D′
A′(-3,1)
B′(1,1)
C′(2,4)
D′(-2,4)
解:如图所示,平移后
各点坐标分别为:
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标
(4,3),B(3,1),C(1,2)
(1)将三角形ABC三
个顶点的横坐标都减去6,
纵坐标不变,分别得到
点A1,B1,C1
(2)依次连接A1,B1,C1,
各点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的 大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 .
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
解:如图所得△ A1B1C1与△ABC的大小、形状完全相同,△ A1B1C1是由△ABC向左平移6个单位得到的
(2)将△ABC三个顶点的纵坐标都减去5,横坐标不变.分别得到点A2,B2,C2
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和位置上有什么关系?
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
解:如图所得△A 2 B 2 C 2与△ABC的大小、形状完全相同,△A 2 B 2 C 2可以看作将△ABC向下平移5个单位得到.
(3)
△ABC三个顶点的坐标分别是
A(-2,-2)、B(-3,-4)、C(-5,-3)
x
0
y
1
2
3
4
-1
-2
-3
-4
1
2
3
4
5
-2
-1
-3
-4
将三角形ABC三个顶点的横坐标都加4,同时纵坐标都加5,得到△ A1B1C1图形又有什么变化?
A
C
B
-5
A
C
B
解:如图所得△ A1B1C1三点的坐标分别是A1(2,3),B1( 1,1),C1(-1,2),依次连接这三点,△ A1B1C1与△ABC的大小、形状完全相同,可以发现△ A1B1C1是由△ABC先向右平移4个单位,再向上平移5个单位得到的。
1
1
1
归纳
P(x, y)
横坐标加a(a>0)
向右平移a个单位
横坐标减a(a>0)
向左平移a个单位
纵坐标加a(a>0)
向上平移a个单位
纵坐标减a(a>0)
向下平移a个单位
点N(-1,3)可以看作由点M(-1,-1)( )
A. 向上平移4个单位长度所得到的
B. 向左平移4个单位长度得到的
C. 向下平移4个单位长度所得到的
D. 向右平移4个单位长度得到的
A
上下平移:上加下减横不变
练习:
已知坐标平面内点A(-2,4),如果将坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的对应点A′的坐标是__________.
(1,2)
三.挑战自我
x
y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
1.有相距5个单位的两点 A(-3,a),B(b,4),AB//x轴,则a= ___ ,b= ___ .
A
B
4
2
四.灵活运用
2.有相距5个单位的两点 A(-3,a),B(b,4),AB//x轴,则a= ___ ,
b= ————.
4
2 或-8
四.灵活运用
向左平移
a个单位
向下平移
个单位
b
向上平移
个单位
b
向右平移
a个单位
小结
P(x, y)
P(x, y-b)
P(x, y+b)
P(x-a, y)
P(x+a, y)
上下平移:
上加下减
横不变
左右平移:左减右加纵不变
由平移方向会写出坐标
由坐标变化能找到平移方向
总
结
一般地,在平面直角坐标系内:
1.如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;
2.如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
7.2.2用坐标表示平移
B
A
C
A′.
1.已知三角形ABC,平移三角形ABC使点A和点A′重合.
2.把鱼往左平移6cm.(假设每小格是1cm)
A
B
体 验 回 顾
1. 什么叫做平移?
2 . 平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移.
平移后图形的位置改变,形状、大小不变.
7.2.2用坐标表示平移
^
y
>
x
0
1
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
1、如图:1、将点A(-2,-3)向右平移5个单位长度,得到点A1( , );
2、将点A(-2,-3)向左平移2个单位长度,得到点A2( , );
A1
-4
-3
3
-3
A2
你发现了什么?
一. 探索图形的平移与图形上点的坐标间的关系
探究
(1)左、右平移:
向右平移a个单位
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
总结规律1:
图形平移与点的坐标变化间的关系
左右平移:左减右加纵不变
探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
3、将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4、将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
你发现了什么?
一. 探索图形的平移与图形上点的坐标间的关系
(2)上、下平移:
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
总结规律2:
图形平移与点的坐标变化间的关系
上下平移:上加下减横不变
我来试一试
1.已知点A(-2,-3):
(1)将点A向右平移5个单位长度得到点A1,则 点A1点
的坐标是 ;
(2)将点A向左平移6个单位长度得到点A2,则 点A2点
的坐标是 ;
(3,-3)
(-8,-3)
右加纵不变
左减纵不变
(3)将点A向上平移3个单位长度得到点A1,则 点A1点
的坐标是 ;
(4)将点A向下平移4个单位长度得到点A2,则 点A2点
的坐标是 ;
上加横不变
下减横不变
左右平移:左减右加纵不变
上下平移:上加下减横不变
(-2,0)
(-2,-7)
2. 将坐标为(-4,-1)的点向右平移2个单位长度,再向上平移3个单位长度,则平移后的点的坐标分别是( )
A.(2,2)
B.(-2,2)
C.(-2,-2)
D.(2,-2)
C
右移横加
上移纵加
如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
课本78页练习
练习:
A′
B′
C′
D′
A′(-3,1)
B′(1,1)
C′(2,4)
D′(-2,4)
解:如图所示,平移后
各点坐标分别为:
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标
(4,3),B(3,1),C(1,2)
(1)将三角形ABC三
个顶点的横坐标都减去6,
纵坐标不变,分别得到
点A1,B1,C1
(2)依次连接A1,B1,C1,
各点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的 大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 .
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
解:如图所得△ A1B1C1与△ABC的大小、形状完全相同,△ A1B1C1是由△ABC向左平移6个单位得到的
(2)将△ABC三个顶点的纵坐标都减去5,横坐标不变.分别得到点A2,B2,C2
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和位置上有什么关系?
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
解:如图所得△A 2 B 2 C 2与△ABC的大小、形状完全相同,△A 2 B 2 C 2可以看作将△ABC向下平移5个单位得到.
(3)
△ABC三个顶点的坐标分别是
A(-2,-2)、B(-3,-4)、C(-5,-3)
x
0
y
1
2
3
4
-1
-2
-3
-4
1
2
3
4
5
-2
-1
-3
-4
将三角形ABC三个顶点的横坐标都加4,同时纵坐标都加5,得到△ A1B1C1图形又有什么变化?
A
C
B
-5
A
C
B
解:如图所得△ A1B1C1三点的坐标分别是A1(2,3),B1( 1,1),C1(-1,2),依次连接这三点,△ A1B1C1与△ABC的大小、形状完全相同,可以发现△ A1B1C1是由△ABC先向右平移4个单位,再向上平移5个单位得到的。
1
1
1
归纳
P(x, y)
横坐标加a(a>0)
向右平移a个单位
横坐标减a(a>0)
向左平移a个单位
纵坐标加a(a>0)
向上平移a个单位
纵坐标减a(a>0)
向下平移a个单位
点N(-1,3)可以看作由点M(-1,-1)( )
A. 向上平移4个单位长度所得到的
B. 向左平移4个单位长度得到的
C. 向下平移4个单位长度所得到的
D. 向右平移4个单位长度得到的
A
上下平移:上加下减横不变
练习:
已知坐标平面内点A(-2,4),如果将坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的对应点A′的坐标是__________.
(1,2)
三.挑战自我
x
y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
1.有相距5个单位的两点 A(-3,a),B(b,4),AB//x轴,则a= ___ ,b= ___ .
A
B
4
2
四.灵活运用
2.有相距5个单位的两点 A(-3,a),B(b,4),AB//x轴,则a= ___ ,
b= ————.
4
2 或-8
四.灵活运用
向左平移
a个单位
向下平移
个单位
b
向上平移
个单位
b
向右平移
a个单位
小结
P(x, y)
P(x, y-b)
P(x, y+b)
P(x-a, y)
P(x+a, y)
上下平移:
上加下减
横不变
左右平移:左减右加纵不变
由平移方向会写出坐标
由坐标变化能找到平移方向
总
结
一般地,在平面直角坐标系内:
1.如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;
2.如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
