【备战2020】中考数学二轮专题 图形运动之旋转边长复习学案(上海地区专用)
文档属性
| 名称 | 【备战2020】中考数学二轮专题 图形运动之旋转边长复习学案(上海地区专用) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 21:04:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
备战2020中考数学二轮专题复习学案
图形运动之旋转边长
【备注】:
1.根据第一个图回顾图形旋转的特征,可以先让学生自己说说,再分析填空;
2.根据第二个图总结图形旋转的常见题型,为后面例题讲解铺垫基础;
3.回顾时可以尽量让学生自己多说,时间大概5分钟。
图形旋转的性质和特征:
图形旋转常见题型:
【备注】:
以下每题教法建议,请老师根据学生实际情况参考;
在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;
可以根据各题的“教法指导”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;
例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;
引导的技巧:直接提醒,问题式引导,类比式引导等等;
部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;
每个题目的讲解时间根据实际情况处理,建议每题2-4分钟,选讲例题在时间足够的情况下讲解。
【参考教法】:旋转边长有关题型可参考以下教法引导学生分析问题、解决问题
1.寻找旋转中心。 提示:让学生说说。
2.寻找旋转的方向,“逆时针”和“顺时针”,如果没有说明则分类讨论。
3.挖掘题目中的特殊条件。题目中有哪些角相等?哪些边相等?找找看。
4.根据题意,计算求解相关边的长度。
5.准确画出旋转后的图形是解题的关键。
【参考提问问题】:①你能找一下旋转的中心吗?
②你能找一下旋转的方向吗?
③题目中由哪些相等的边、角?你找找看。
④你能大致的画一下旋转后的图形吗?
三.典型例题
把边长为的等边三角形ABC绕着点C旋转90度后,点A落在点处,那么线段的长等于 cm。(★★★)
【答案】
【提示】画图(如下图),分顺时针和逆时针两个情况,根据图象可以的,
,则。
例2.如图,在直角坐标平面内,中,,,,如果
绕原点 按顺时针方向旋转到的位置,那么点的坐标是 。(★★★)
【答案】:。
【提示】过画轴垂线可得。
如图, 等腰△ABC中,AB=AC,BC=2cm,∠A=1200,将△ABC绕着点A旋转,当点B落在点C的位置时,点C落在点D处,则BD的长为_________cm。(★★★)
【答案】2
【提示】证明为等边三角形即可。
如图,边长为3的正方形绕点按逆时针方向旋转后得到的正方形,交于点,那么的长为_______.(★★★★)
【答案】
【提示】联结,证明,则可得,用三角比即可求解。
对应练习
练习1.如图,在中,∠ACB=,AC=4,BC=3,将绕点C顺时针旋转至的位置,其中B1C⊥AB,B1C、A1B1交AB于M、N两点,则线段MN的长为 。(★★★★)
【答案】。
【提示】可求得,则,求得。
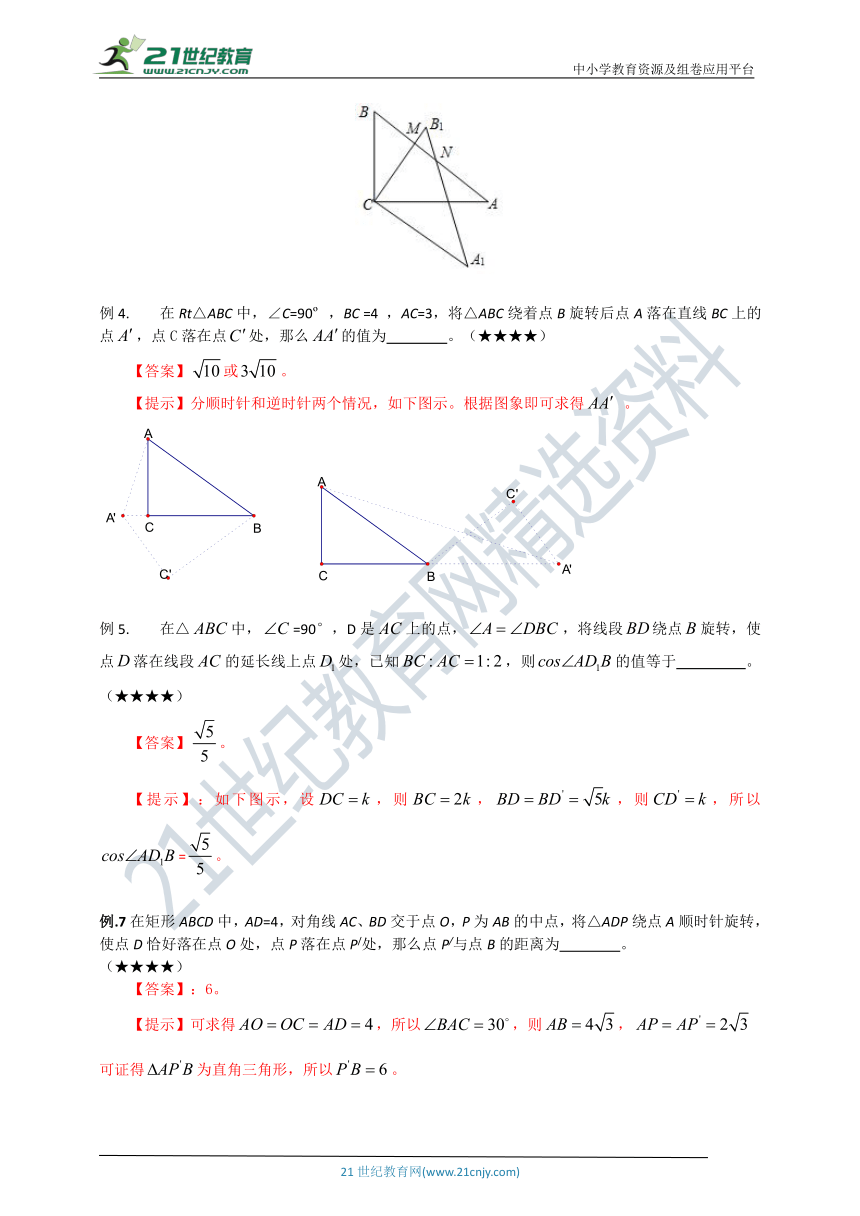
在Rt△ABC中,∠C=90? ,BC =4 ,AC=3,将△ABC绕着点B旋转后点A落在直线BC上的点,点C落在点处,那么的值为 。(★★★★)
【答案】或。
【提示】分顺时针和逆时针两个情况,如下图示。根据图象即可求得 。
在△中,=90°,D是上的点,,将线段绕点旋转,使点落在线段的延长线上点处,已知,则的值等于 。(★★★★)
【答案】。
【提示】:如下图示,设,则,,则,所以=。
例.7在矩形ABCD中,AD=4,对角线AC、BD交于点O,P为AB的中点,将△ADP绕点A顺时针旋转,使点D恰好落在点O处,点P落在点P/处,那么点P/与点B的距离为 。
(★★★★)
【答案】:6。
【提示】可求得,所以,则,
可证得为直角三角形,所以。
对应练习
练习1.已知P是正方形ABCD内一点,将△ABP绕点B旋转,使得边BA与边BC重合,点P落在点的位置上.如果PB=3,那么的长等于 。(★★★)
【答案】。
练习2.点A的坐标为(,0),把点A绕着坐标原点顺时针旋转135?到点B,那么点B的坐标是 _________ 。(★★★)
【答案】
练习3.如下左图,已知,将绕点逆时针旋转15°后得到,与交于点, 若,则= 。(★★★★)
【答案】
【提示】,,用三角比即可求解。
【备注】:本部分对前面例题中讲到的解题方法进行归类总结,以引导式总结出,建议时间4分钟左右。
图形旋转之“旋转边长”题型解题方法与策略:
1.寻找点,即旋转中心;
2.寻找旋转的方向,“逆时针”和“顺时针”,如果没有说明则分类讨论。;
3.寻找旋转相等的线段或角度;
4.利用旋转并结合题目中的特殊条件解题;
5.部分题目注意分类讨论;
6.准确画出旋转后的图形是解题的关键。
巩固练习
【备注】:该部分让学生独立完成,之后评分并讲解,每题4分,共36分,15分钟完成。
1.如上右图,将绕点逆时针旋转,得到.若点的坐标为,
则点的坐标为 。(★★★)
【答案】
【提示】,对应边相等。
如图,已知在直角三角形ABC中,∠C=90°,AB=5,BC=3,将绕着点B顺时针旋转,使点C落在边AB上的点C′处,点A落在点A′处,则AA′的长为 。(★★★★)
【答案】。
【提示】如下图是示,可求解得,则可得 。
将等腰△绕着底边的中点旋转30°后,如果点恰好落在原△的边上,那么∠的余切值等于 。(★★★)
【答案】
在中,,是上的点,,将线段绕点旋转,使点
落在线段的延长线上,记作点,已知,,则 。
(★★★★)
【答案】2。
在△中,∠=90°,,,△绕着点旋转后, 点落在边上的点,点落在点,那么的值为 。(★★★)
【答案】
已知A是平面直角坐标系内一点,先把点A向上平移3个单位得到点B,再把点A绕点B顺时针方向旋转90°得到点C,若点C关于y轴的对称点为(1,2),那么点A的坐标是 .(★★★★)
【答案】。
如图,在△ABC中,∠C=90?,∠A=30?,BC=1,将△ABC绕点 B顺时针方向旋转,使点C落到AB的延长线上,那么点A所经过的线路长为 。(★★★★)
【答案】
8.已知△中,∠,,, 把△绕着点旋转,使得点落在点,点落在点.若点在边上,则点、的距离为 。(★★★)
【答案】。
如图,在等边中,,点在上,且,点是上一动点,连结.将线段绕点逆时针旋转旷得到线段要使点恰好落在上,则的长是 。(★★★★)
【答案】6
y
x
A
B
O
A
B
C
D
E
F
G
H
图
A
B
C
(第图)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
