2020春华师版九下数学 27.1.3圆周角 课件(35张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.1.3圆周角 课件(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:07:51 | ||
图片预览










文档简介
课件35张PPT。3.圆 周 角 1.圆周角
(1)圆周角的定义
顶点在___上,并且两边都和圆_____的角叫做圆周角.
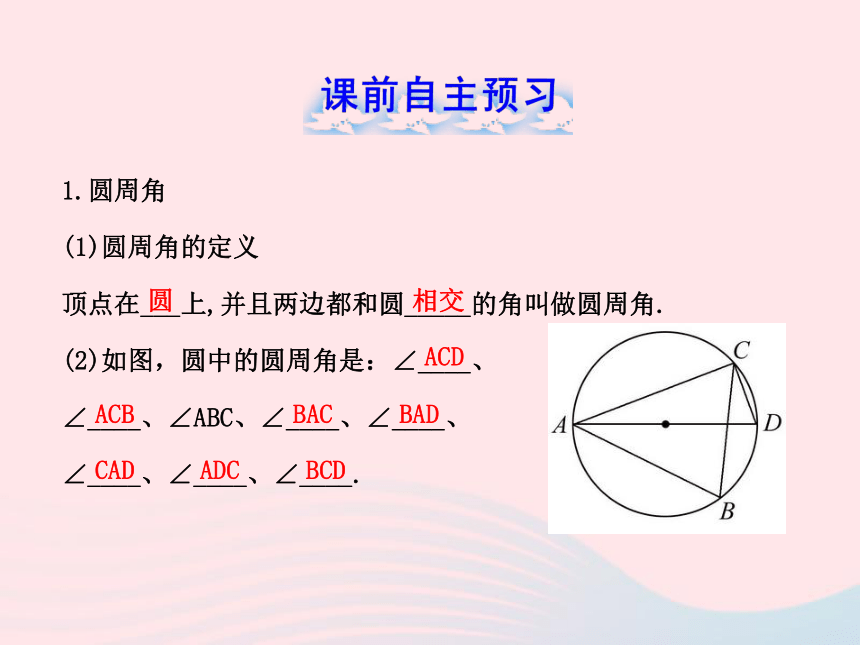
(2)如图,圆中的圆周角是:∠____、
∠____、∠ABC、∠____、∠____、
∠____、∠____、∠____.圆相交ACDACBBACBADCADADCBCD2.圆周角定理及推论
(1)圆周角的定理
在同圆或等圆中,同弧或等弧所对的圆周角_____,都等于这条弧
所对的圆心角的_____;相等的圆周角所对的弧_____.相等一半相等(2)推论
半圆或直径所对的圆周角都_____,都等于_____.90°的圆周
角所对的弦是圆的_____.
用符号语言来表示:
如图:①∵AB是⊙O的直径,
∴∠ACB=90°;
②∵∠ACB=90°,
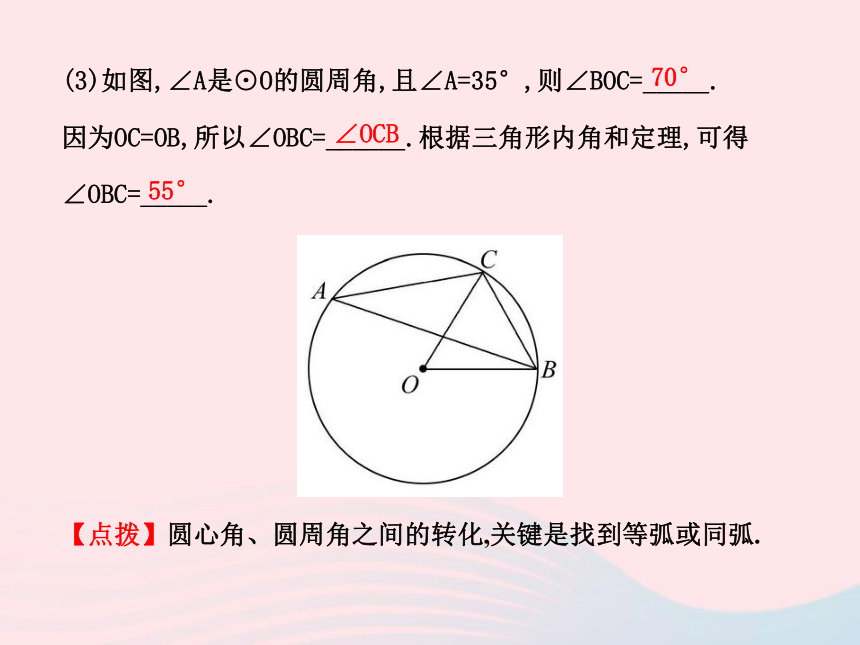
∴AB是⊙O的直径. 相等90°直径(3)如图,∠A是⊙O的圆周角,且∠A=35°,则∠BOC=_____.
因为OC=OB,所以∠OBC=______.根据三角形内角和定理,可得
∠OBC=_____.
【点拨】圆心角、圆周角之间的转化,关键是找到等弧或同弧. 70°∠OCB55°【预习思考】表示圆周角时应注意什么问题?
提示:(1)三个字母表示时,应按顺序写,且表示顶点的字母在
中间;
(2)单独一个字母表示时,用表示顶点的字母即圆上的点来表示. 弧、圆周角、圆心角的关系
【例1】如图,BD是
⊙O的直径,A,C是⊙O上的两点,且
AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长. 【解题探究】(1)①在△ABD和△AEB中,有相等的角吗?
答:有一对公共角,∠BAD=∠EAB.
②如何找出另一组角相等?
答:∵AB=AC,∴ ,根据圆周角定理可得∠ADB=∠ABE.
③由①②可知△ABD和△AEB中有两对对应角相等,所以
△ABD∽△AEB. (2)①由(1)中所得到的相似三角形,如何求出AB?
答:∵△ABD∽△AEB,
∴ .
∴AB2=AD·AE=4.
∴AB=2.
②如何求出BD的长?
答:∵BD是⊙O的直径,∴∠DAB=90°
在Rt△ABD中,BD2=AB2+AD2=5.
∴BD= . 【互动探究】圆周角和圆心角、弧的关系是什么?
提示:(1)由于圆心角的度数等于它所对的弧的度数,所以圆周
角的度数等于它所对的弧的度数的一半.
(2)在同圆或等圆中,相等的圆周角所对的弧相等.【规律总结】
利用圆周角定理进行证明时的两点注意
1.圆周角定理适用的范围是在同圆或等圆中;
2.在证明时,此定理可以直接作为已知条件使用.【跟踪训练】
1.已知:如图,OA,OB是
⊙O的两条半径,且OA⊥OB,点C在⊙O上,
则∠ACB的度数为( )
(A)45° (B)35°
(C)25° (D)20°
【解析】选A.因为OA⊥OB,所以∠AOB=90°,由圆周角定
理可知∠ACB=45°.2.如图,若AB是⊙O的直径,CD是⊙O的
弦,∠ABD=55°,则∠BCD的度数为( )
(A)35° (B)45° (C)55° (D)75°【解析】选A.连结AD,∵AB是⊙O的直径,∴∠ADB=90°,
∴∠A=90°-55°=35°,根据同弧所对的圆周角相等可得
∠BCD=∠A=35°.3.如图,△ABC内接于⊙O,已知∠A=55°,则∠BOC=______.
【解析】根据圆周角和圆心角的关系可得∠BOC=2∠A=110°.
答案:110° 圆周角定理的综合应用
【例2】(8分)如图,AB是⊙O的直径,C是
的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,则⊙O的半径为______,
CE的长是_______.
易错提醒:利用圆周角定理找出相等的角,是解决该题关键的
一步. 【规范解答】(1)∵AB是⊙O的直径,∴∠ACE+∠2=90°,
又∵CE⊥AB,∴∠AEC=90°,即∠A+∠ACE=90°
∴∠2=∠A ………………………………………………3分
又∵C是 的中点,
∴∠1=∠A,∴∠1=∠2.…………………………………4分
∴CF=BF.…………………………………………………5分(2)由题意得∠ACB=90°,
又∵BC=CD=6,AC=8,
∴AB= ∴⊙O的半径为5.……………………6分
由面积公式得 ,解得CE= .
∴CE的长是 .………………………………………………8分【规律总结】
利用圆周角定理推论的两种思路
1.见直径,通常构建90°的圆周角,利用直角三角形知识解决;
2.见90°的圆周角,通常作直径,构建直角三角形.【跟踪训练】
4.如图,已知BD是⊙O直
径,点A,C在⊙O上, ∠AOB=60°,
则∠BDC的度数是( )
(A)20° (B)25°
(C)30° (D)40°
【解析】选C.连结OC,因为同弧或等弧所对的
圆心角相等,所以∠AOB=∠BOC=60°,所以∠D=30°. 【变式训练】如图,以原点O为圆心的圆交x轴
于A,B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,
若∠DAB=20°,则∠OCD=__________.【解析】连结DO,∵∠DAB=20°,∴∠DOB=40°,
∴∠COD=90°-40°=50°,∵CO=DO,
∴∠OCD=∠CDO,∴∠OCD=(180°-50°)÷2=65°.
答案:65°5.如图,⊙O是△ABC的
外接圆,连结OB,OC,若OB=BC,则∠BAC
等于( )
(A)60° (B)45° (C)30° (D)20°
【解析】选C.因为OB=BC=OC,所以△OBC是等边三角形,则
∠BOC=60°.因为同弧所对的圆周角等于圆心角的一半,所以
∠BAC=30°,故选C.6.如图,在⊙O中,直径AB与弦CD相交于
点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知AD=6,求圆心O到BD的距离.【解析】(1)∵∠APD=∠C+∠CAB,
∴∠C=65°-40°=25°,
∴∠B=∠C=25°.
(2)作OE⊥BD于E,则DE=BE,
又∵AO=BO,
∴OE=
圆心O到BD的距离为3.1.如图,∠AOB=100°,点C在⊙O上,且点C
不与A,B重合,则∠ACB的度数为( )
(A)50° (B)80°或50° (C)130° (D)50°或130°【解析】选D.利用同弧所对的圆周角是圆心角的一半,求得圆周
角的度数即可,注意点C可能在优弧上也可能在劣弧上,分两种情
况讨论.当点C在优弧上时, 当点C
在劣弧上时, =130°.2.如图所示,已知⊙O是△ABC的外接圆,AD
是⊙O的直径,连结CD,若AD=3,AC=2,则cos B的值为( )
【解析】选B.∵∠B和∠D所对的弧是 ,根据同弧所对的圆周
角相等,
∴∠B=∠D.
又∵AD是直径,
∴∠ACD=90°,
根据勾股定理,得
∴cos B=cos D=3.如图,将三角板的直角顶点放在⊙O的圆心
上,两条直角边分别交⊙O于A,B两点,点P在
优弧AB上,且与点A,B不重合,连结PA,PB.
则∠APB的大小为_______度.
【解析】∠AOB为圆心角,其值为90°,∠APB为同弧上的圆周角,
其大小为∠AOB的一半,所以∠APB=
答案:454.如图,已知∠OCB=20°,则∠A=_______度.
【解析】∵OB=OC,∴∠OBC=∠OCB=20°,
∴∠O=180°-∠OBC-∠OCB=140°,
∴∠A=
答案:705.如图,点P为等边△ABC外接圆劣弧BC上
一点.
(1)求∠BPC的度数;
(2)求证:PA=PB+PC;
(3)设PA,BC交于点M,若AB=4,PC=2,求CM
的长度.【解析】(1)∵△ABC为等边三角形,∴∠BAC=60°.
∵点P为等边△ABC外接圆劣弧BC上一点,
∴∠BPC+∠BAC=180°,
∴∠BPC=120°. (2)在PA上截取PD=PC,
∵AB=AC=BC,∴∠APB=∠APC=60°,
∴△PCD为等边三角形,
∴∠ADC=120°,
∴△ACD≌△BCP,
∴AD=PB,
∴PA=PB+PC;(3)∵△CDM∽△ACM,∴CM∶AM=DM∶MC=DC∶AC=2∶4=1∶2,
设DM=x,则CM=2x,BM=4-2x,PM=2-x,AM=4x.
∵△BPM∽△ACM.∴BP∶AC=PM∶CM,即3x∶4=(2-x)∶2x.
解得 (舍去负号),则
∴CM=
(1)圆周角的定义
顶点在___上,并且两边都和圆_____的角叫做圆周角.
(2)如图,圆中的圆周角是:∠____、
∠____、∠ABC、∠____、∠____、
∠____、∠____、∠____.圆相交ACDACBBACBADCADADCBCD2.圆周角定理及推论
(1)圆周角的定理
在同圆或等圆中,同弧或等弧所对的圆周角_____,都等于这条弧
所对的圆心角的_____;相等的圆周角所对的弧_____.相等一半相等(2)推论
半圆或直径所对的圆周角都_____,都等于_____.90°的圆周
角所对的弦是圆的_____.
用符号语言来表示:
如图:①∵AB是⊙O的直径,
∴∠ACB=90°;
②∵∠ACB=90°,
∴AB是⊙O的直径. 相等90°直径(3)如图,∠A是⊙O的圆周角,且∠A=35°,则∠BOC=_____.
因为OC=OB,所以∠OBC=______.根据三角形内角和定理,可得
∠OBC=_____.
【点拨】圆心角、圆周角之间的转化,关键是找到等弧或同弧. 70°∠OCB55°【预习思考】表示圆周角时应注意什么问题?
提示:(1)三个字母表示时,应按顺序写,且表示顶点的字母在
中间;
(2)单独一个字母表示时,用表示顶点的字母即圆上的点来表示. 弧、圆周角、圆心角的关系
【例1】如图,BD是
⊙O的直径,A,C是⊙O上的两点,且
AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长. 【解题探究】(1)①在△ABD和△AEB中,有相等的角吗?
答:有一对公共角,∠BAD=∠EAB.
②如何找出另一组角相等?
答:∵AB=AC,∴ ,根据圆周角定理可得∠ADB=∠ABE.
③由①②可知△ABD和△AEB中有两对对应角相等,所以
△ABD∽△AEB. (2)①由(1)中所得到的相似三角形,如何求出AB?
答:∵△ABD∽△AEB,
∴ .
∴AB2=AD·AE=4.
∴AB=2.
②如何求出BD的长?
答:∵BD是⊙O的直径,∴∠DAB=90°
在Rt△ABD中,BD2=AB2+AD2=5.
∴BD= . 【互动探究】圆周角和圆心角、弧的关系是什么?
提示:(1)由于圆心角的度数等于它所对的弧的度数,所以圆周
角的度数等于它所对的弧的度数的一半.
(2)在同圆或等圆中,相等的圆周角所对的弧相等.【规律总结】
利用圆周角定理进行证明时的两点注意
1.圆周角定理适用的范围是在同圆或等圆中;
2.在证明时,此定理可以直接作为已知条件使用.【跟踪训练】
1.已知:如图,OA,OB是
⊙O的两条半径,且OA⊥OB,点C在⊙O上,
则∠ACB的度数为( )
(A)45° (B)35°
(C)25° (D)20°
【解析】选A.因为OA⊥OB,所以∠AOB=90°,由圆周角定
理可知∠ACB=45°.2.如图,若AB是⊙O的直径,CD是⊙O的
弦,∠ABD=55°,则∠BCD的度数为( )
(A)35° (B)45° (C)55° (D)75°【解析】选A.连结AD,∵AB是⊙O的直径,∴∠ADB=90°,
∴∠A=90°-55°=35°,根据同弧所对的圆周角相等可得
∠BCD=∠A=35°.3.如图,△ABC内接于⊙O,已知∠A=55°,则∠BOC=______.
【解析】根据圆周角和圆心角的关系可得∠BOC=2∠A=110°.
答案:110° 圆周角定理的综合应用
【例2】(8分)如图,AB是⊙O的直径,C是
的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,则⊙O的半径为______,
CE的长是_______.
易错提醒:利用圆周角定理找出相等的角,是解决该题关键的
一步. 【规范解答】(1)∵AB是⊙O的直径,∴∠ACE+∠2=90°,
又∵CE⊥AB,∴∠AEC=90°,即∠A+∠ACE=90°
∴∠2=∠A ………………………………………………3分
又∵C是 的中点,
∴∠1=∠A,∴∠1=∠2.…………………………………4分
∴CF=BF.…………………………………………………5分(2)由题意得∠ACB=90°,
又∵BC=CD=6,AC=8,
∴AB= ∴⊙O的半径为5.……………………6分
由面积公式得 ,解得CE= .
∴CE的长是 .………………………………………………8分【规律总结】
利用圆周角定理推论的两种思路
1.见直径,通常构建90°的圆周角,利用直角三角形知识解决;
2.见90°的圆周角,通常作直径,构建直角三角形.【跟踪训练】
4.如图,已知BD是⊙O直
径,点A,C在⊙O上, ∠AOB=60°,
则∠BDC的度数是( )
(A)20° (B)25°
(C)30° (D)40°
【解析】选C.连结OC,因为同弧或等弧所对的
圆心角相等,所以∠AOB=∠BOC=60°,所以∠D=30°. 【变式训练】如图,以原点O为圆心的圆交x轴
于A,B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,
若∠DAB=20°,则∠OCD=__________.【解析】连结DO,∵∠DAB=20°,∴∠DOB=40°,
∴∠COD=90°-40°=50°,∵CO=DO,
∴∠OCD=∠CDO,∴∠OCD=(180°-50°)÷2=65°.
答案:65°5.如图,⊙O是△ABC的
外接圆,连结OB,OC,若OB=BC,则∠BAC
等于( )
(A)60° (B)45° (C)30° (D)20°
【解析】选C.因为OB=BC=OC,所以△OBC是等边三角形,则
∠BOC=60°.因为同弧所对的圆周角等于圆心角的一半,所以
∠BAC=30°,故选C.6.如图,在⊙O中,直径AB与弦CD相交于
点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知AD=6,求圆心O到BD的距离.【解析】(1)∵∠APD=∠C+∠CAB,
∴∠C=65°-40°=25°,
∴∠B=∠C=25°.
(2)作OE⊥BD于E,则DE=BE,
又∵AO=BO,
∴OE=
圆心O到BD的距离为3.1.如图,∠AOB=100°,点C在⊙O上,且点C
不与A,B重合,则∠ACB的度数为( )
(A)50° (B)80°或50° (C)130° (D)50°或130°【解析】选D.利用同弧所对的圆周角是圆心角的一半,求得圆周
角的度数即可,注意点C可能在优弧上也可能在劣弧上,分两种情
况讨论.当点C在优弧上时, 当点C
在劣弧上时, =130°.2.如图所示,已知⊙O是△ABC的外接圆,AD
是⊙O的直径,连结CD,若AD=3,AC=2,则cos B的值为( )
【解析】选B.∵∠B和∠D所对的弧是 ,根据同弧所对的圆周
角相等,
∴∠B=∠D.
又∵AD是直径,
∴∠ACD=90°,
根据勾股定理,得
∴cos B=cos D=3.如图,将三角板的直角顶点放在⊙O的圆心
上,两条直角边分别交⊙O于A,B两点,点P在
优弧AB上,且与点A,B不重合,连结PA,PB.
则∠APB的大小为_______度.
【解析】∠AOB为圆心角,其值为90°,∠APB为同弧上的圆周角,
其大小为∠AOB的一半,所以∠APB=
答案:454.如图,已知∠OCB=20°,则∠A=_______度.
【解析】∵OB=OC,∴∠OBC=∠OCB=20°,
∴∠O=180°-∠OBC-∠OCB=140°,
∴∠A=
答案:705.如图,点P为等边△ABC外接圆劣弧BC上
一点.
(1)求∠BPC的度数;
(2)求证:PA=PB+PC;
(3)设PA,BC交于点M,若AB=4,PC=2,求CM
的长度.【解析】(1)∵△ABC为等边三角形,∴∠BAC=60°.
∵点P为等边△ABC外接圆劣弧BC上一点,
∴∠BPC+∠BAC=180°,
∴∠BPC=120°. (2)在PA上截取PD=PC,
∵AB=AC=BC,∴∠APB=∠APC=60°,
∴△PCD为等边三角形,
∴∠ADC=120°,
∴△ACD≌△BCP,
∴AD=PB,
∴PA=PB+PC;(3)∵△CDM∽△ACM,∴CM∶AM=DM∶MC=DC∶AC=2∶4=1∶2,
设DM=x,则CM=2x,BM=4-2x,PM=2-x,AM=4x.
∵△BPM∽△ACM.∴BP∶AC=PM∶CM,即3x∶4=(2-x)∶2x.
解得 (舍去负号),则
∴CM=
