2020春华师版九下数学 27.2.2直线与圆的位置关系课件(25张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.2.2直线与圆的位置关系课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览






文档简介
课件25张PPT。2.直线与圆的位置关系 1.直线与圆的位置关系有哪几种?
答:直线与圆有_____位置关系:_____、_____和_____.三种相交相切相离2.如何用语言描述三种位置关系?
答:(1)直线和圆有_____公共点时,叫做直线和圆相交.直线叫做
圆的_____;
(2)直线和圆_________公共点时,叫做直线和圆相切.直线叫圆的
_____,这个公共点叫做_____;
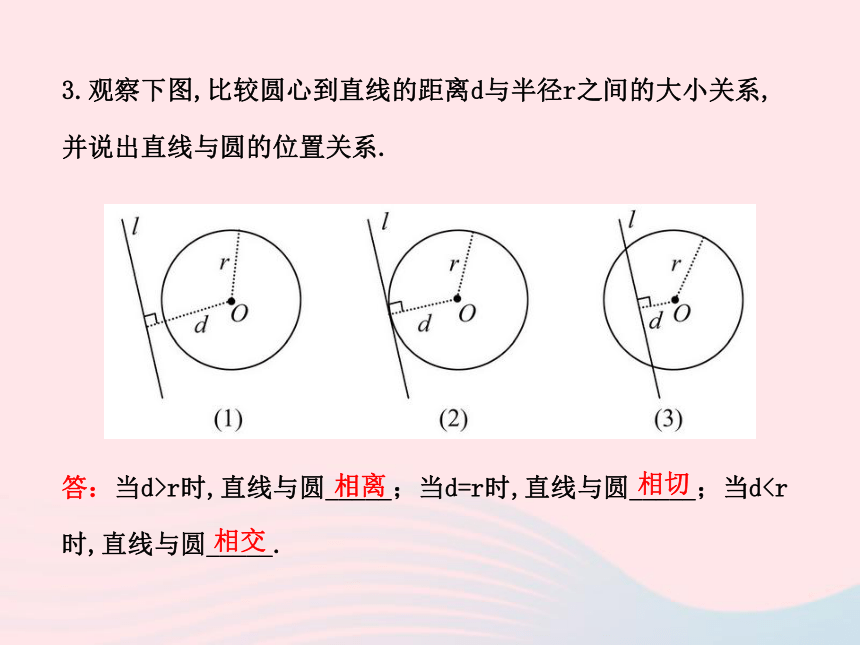
(3)直线和圆_____公共点时,叫做直线和圆_____.两个割线只有一个切线切点没有相离3.观察下图,比较圆心到直线的距离d与半径r之间的大小关系,
并说出直线与圆的位置关系.
答:当d>r时,直线与圆_____;当d=r时,直线与圆_____;当d时,直线与圆_____.相离相切相交【归纳】如果⊙O的半径为r,圆心O到直线l的距离为d,那么:
(1)直线l和⊙O_____?d>r;
(2)直线l和⊙O_____?d=r;
(3)直线l和⊙O_____?d<r.相离相切相交【预习思考】判断命题“直线与圆有一个公共点时,叫做直线与
圆相切”是真命题还是假命题.
提示:假命题.直线与圆有唯一公共点时,直线和圆相切,是指直
线与圆“有且只有一个公共点”,它与“一个公共点”含义不
同. 直线与圆的位置关系的判定
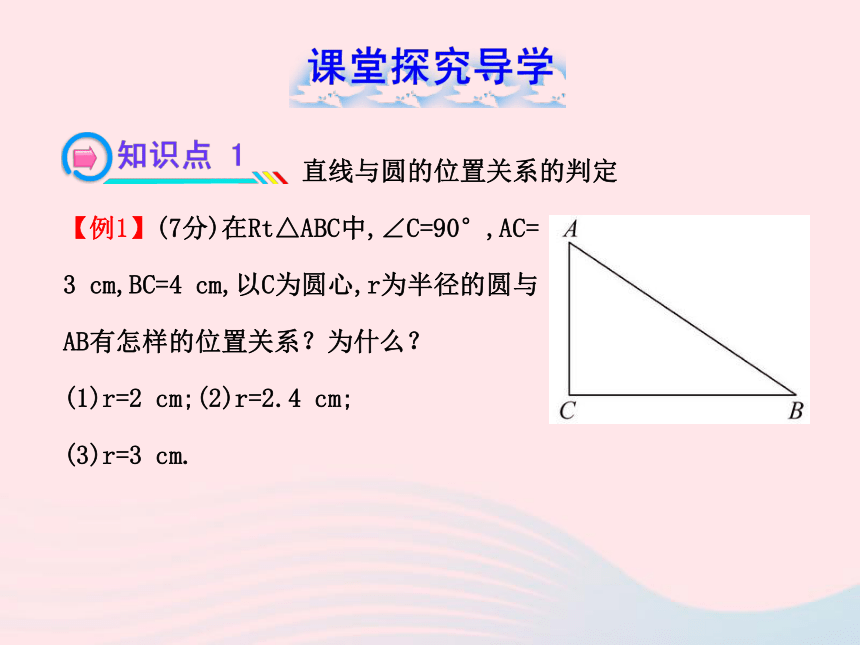
【例1】(7分)在Rt△ABC中,∠C=90°,AC=
3 cm,BC=4 cm,以C为圆心,r为半径的圆与
AB有怎样的位置关系?为什么?
(1)r=2 cm;(2)r=2.4 cm;
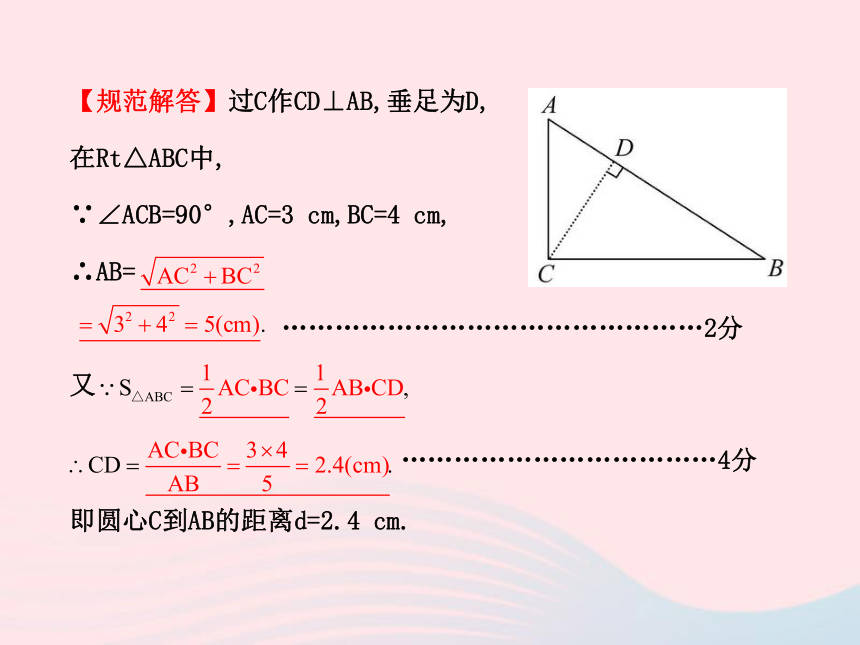
(3)r=3 cm. 【规范解答】过C作CD⊥AB,垂足为D,
在Rt△ABC中,
∵∠ACB=90°,AC=3 cm,BC=4 cm,
∴AB=
…………………………………………2分
又
………………………………4分
即圆心C到AB的距离d=2.4 cm.①当r=2 cm时,有d>r,因此⊙C和AB相离.
………………………………………………………………5分
②当r=2.4 cm时,有d=r,因此⊙C和AB相切.
……………………………………………………………… 6分
③当r=3 cm时,有d……………………………………………………………… 7分【互动探究】直线与圆除了上述三种位置关系外,是否还有第
四种关系?直线与圆的公共点是否能多于两个?
提示:由于经过同一直线上的三点不可能作圆,因而直线不可
能与圆有三个公共点,故直线与圆不可能有第四种关系,公共
点不可能多于两个.【规律总结】
直线与圆的位置关系直线与圆的位置关系相离相切相交公共点的个数012圆心到直线的距离d
与半径r的关系d>rd=rd1.如果一个圆的半径是8 cm,圆心到一条直线的距离也是8 cm,
那么这条直线和这个圆的位置关系是( )
(A)相离 (B)相交
(C)相切 (D)不能确定
【解析】选C.∵圆的半径是8 cm,圆心到直线的距离也是8 cm,
∴直线与圆相切.2.已知⊙O的半径为3 cm,点P是直线l上一点,OP长为5 cm,则直
线l与⊙O的位置关系为( )
(A)相交 (B)相切
(C)相离 (D)相交、相切、相离都有可能
【解析】选D.因为垂线段最短,所以圆心到直线的距离小于等于
5.此时它和半径的大小关系不确定,则直线和圆相交、相切、相
离都有可能. 3.在Rt△ABC中,∠A=30°,直角边AC=6 cm,以
C为圆心,3 cm长为半径作圆,则⊙C与AB的位置关系是________.
【解析】根据题意画出图形,如图所示:
过C作CD⊥AB,交AB于点D,
在Rt△ACD中,AC=6 cm,∠A=30°,
∴ 又∵圆C的半径为3 cm,
∴⊙C与AB的位置关系是相切.
答案:相切 直线与圆的位置关系的性质
【例2】如图,Rt△ABC中,∠C=90°,AC=3,
AB=5,若以C为圆心,r为半径作圆,那么当
直线AB与⊙C相离、相切、相交时,分别求
r的取值范围.
【解题探究】(1)利用勾股定理可求出BC=4;
(2)过点C作CD⊥AB于点D,则 CD=2.4; (3)当直线AB与⊙C相离时,点C到AB的距离
大于⊙C的半径r;
(4)当直线AB与⊙C相切时,点C到AB的距离
等于⊙C的半径r;
(5)当直线AB与⊙C相交时,点C到AB的距离
小于⊙C的半径r;
所以当直线AB与⊙C相离、相切、相交时,r的取值范围分别为:
小于2.4、等于2.4和大于2.4.【规律总结】
d,r与直线和圆的位置关系
1.由d和r可推出直线和圆的位置关系;
2.由直线和圆的位置关系,可比较d和r的大小;
3.已知d和位置关系可求r的范围;
4.已知r和位置关系可求d的范围.【跟踪训练】
4.⊙O的半径为r,直线l与⊙O有公共点,且圆心O到直线l的距
离为d,则d与r的关系是( )
(A)d<r (B)d=r (C)d>r (D)d≤r
【解析】选D.由直线l与⊙O有公共点,可知直线与圆相切或相
交,则直线到圆心的距离不大于圆的半径,即d≤r.5.已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,
如果圆上有且只有两点到直线l的距离均为2,则半径r的取值范
围是( )
(A)r>1 (B)r>2 (C)1<r<2 (D)1<r<5
【解析】选D.根据题意可知,若使圆上有且只有两点到直线l的
距离均为2,则当圆与直线l相离时,r>1;当圆与直线l相交
时,r<5.所以1l4的位置关系.若圆O的半径为20 cm,且O点
到其中一直线的距离为14 cm,则此直线
为( )
(A)l1 (B)l2 (C)l3 (D)l4
【解析】选B.因为所求直线到圆心O点的距离为14 cm<20 cm,所
以此直线为圆O的割线,即为直线l2. 2.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4 cm,以点C为圆
心,以2 cm为半径作圆,则⊙C与AB的位置关系是( )
(A)相离 (B)相切
(C)相交 (D)相切或相交【解析】选B.作CD⊥AB于点D.
∵∠B=30°,BC=4 cm,
∴CD=2 cm,等于半径.
∴AB与⊙C相切.3.如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),
当该圆向上平移______个单位时,它与x轴相切.【解析】设圆的半径为r,圆心到直线的距离为d,要使圆与x轴相
切,必须使d=r.∵此时d=3,∴圆向上平移1或5个单位时,它与x轴
相切.
答案:1或54.如图,在矩形ABCD中,AB=6,BC=4,⊙O是以AB为直径的圆,试说明直线DC与⊙O的位置关系.
【解析】∵矩形ABCD中,BC=4,
∴圆心到CD的距离为4.∵AB为直径,AB=6,
∴半径是3.∵4>3,∴直线DC与⊙O相离.
答:直线与圆有_____位置关系:_____、_____和_____.三种相交相切相离2.如何用语言描述三种位置关系?
答:(1)直线和圆有_____公共点时,叫做直线和圆相交.直线叫做
圆的_____;
(2)直线和圆_________公共点时,叫做直线和圆相切.直线叫圆的
_____,这个公共点叫做_____;
(3)直线和圆_____公共点时,叫做直线和圆_____.两个割线只有一个切线切点没有相离3.观察下图,比较圆心到直线的距离d与半径r之间的大小关系,
并说出直线与圆的位置关系.
答:当d>r时,直线与圆_____;当d=r时,直线与圆_____;当d
(1)直线l和⊙O_____?d>r;
(2)直线l和⊙O_____?d=r;
(3)直线l和⊙O_____?d<r.相离相切相交【预习思考】判断命题“直线与圆有一个公共点时,叫做直线与
圆相切”是真命题还是假命题.
提示:假命题.直线与圆有唯一公共点时,直线和圆相切,是指直
线与圆“有且只有一个公共点”,它与“一个公共点”含义不
同. 直线与圆的位置关系的判定
【例1】(7分)在Rt△ABC中,∠C=90°,AC=
3 cm,BC=4 cm,以C为圆心,r为半径的圆与
AB有怎样的位置关系?为什么?
(1)r=2 cm;(2)r=2.4 cm;
(3)r=3 cm. 【规范解答】过C作CD⊥AB,垂足为D,
在Rt△ABC中,
∵∠ACB=90°,AC=3 cm,BC=4 cm,
∴AB=
…………………………………………2分
又
………………………………4分
即圆心C到AB的距离d=2.4 cm.①当r=2 cm时,有d>r,因此⊙C和AB相离.
………………………………………………………………5分
②当r=2.4 cm时,有d=r,因此⊙C和AB相切.
……………………………………………………………… 6分
③当r=3 cm时,有d
四种关系?直线与圆的公共点是否能多于两个?
提示:由于经过同一直线上的三点不可能作圆,因而直线不可
能与圆有三个公共点,故直线与圆不可能有第四种关系,公共
点不可能多于两个.【规律总结】
直线与圆的位置关系直线与圆的位置关系相离相切相交公共点的个数012圆心到直线的距离d
与半径r的关系d>rd=rd
那么这条直线和这个圆的位置关系是( )
(A)相离 (B)相交
(C)相切 (D)不能确定
【解析】选C.∵圆的半径是8 cm,圆心到直线的距离也是8 cm,
∴直线与圆相切.2.已知⊙O的半径为3 cm,点P是直线l上一点,OP长为5 cm,则直
线l与⊙O的位置关系为( )
(A)相交 (B)相切
(C)相离 (D)相交、相切、相离都有可能
【解析】选D.因为垂线段最短,所以圆心到直线的距离小于等于
5.此时它和半径的大小关系不确定,则直线和圆相交、相切、相
离都有可能. 3.在Rt△ABC中,∠A=30°,直角边AC=6 cm,以
C为圆心,3 cm长为半径作圆,则⊙C与AB的位置关系是________.
【解析】根据题意画出图形,如图所示:
过C作CD⊥AB,交AB于点D,
在Rt△ACD中,AC=6 cm,∠A=30°,
∴ 又∵圆C的半径为3 cm,
∴⊙C与AB的位置关系是相切.
答案:相切 直线与圆的位置关系的性质
【例2】如图,Rt△ABC中,∠C=90°,AC=3,
AB=5,若以C为圆心,r为半径作圆,那么当
直线AB与⊙C相离、相切、相交时,分别求
r的取值范围.
【解题探究】(1)利用勾股定理可求出BC=4;
(2)过点C作CD⊥AB于点D,则 CD=2.4; (3)当直线AB与⊙C相离时,点C到AB的距离
大于⊙C的半径r;
(4)当直线AB与⊙C相切时,点C到AB的距离
等于⊙C的半径r;
(5)当直线AB与⊙C相交时,点C到AB的距离
小于⊙C的半径r;
所以当直线AB与⊙C相离、相切、相交时,r的取值范围分别为:
小于2.4、等于2.4和大于2.4.【规律总结】
d,r与直线和圆的位置关系
1.由d和r可推出直线和圆的位置关系;
2.由直线和圆的位置关系,可比较d和r的大小;
3.已知d和位置关系可求r的范围;
4.已知r和位置关系可求d的范围.【跟踪训练】
4.⊙O的半径为r,直线l与⊙O有公共点,且圆心O到直线l的距
离为d,则d与r的关系是( )
(A)d<r (B)d=r (C)d>r (D)d≤r
【解析】选D.由直线l与⊙O有公共点,可知直线与圆相切或相
交,则直线到圆心的距离不大于圆的半径,即d≤r.5.已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,
如果圆上有且只有两点到直线l的距离均为2,则半径r的取值范
围是( )
(A)r>1 (B)r>2 (C)1<r<2 (D)1<r<5
【解析】选D.根据题意可知,若使圆上有且只有两点到直线l的
距离均为2,则当圆与直线l相离时,r>1;当圆与直线l相交
时,r<5.所以1
到其中一直线的距离为14 cm,则此直线
为( )
(A)l1 (B)l2 (C)l3 (D)l4
【解析】选B.因为所求直线到圆心O点的距离为14 cm<20 cm,所
以此直线为圆O的割线,即为直线l2. 2.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4 cm,以点C为圆
心,以2 cm为半径作圆,则⊙C与AB的位置关系是( )
(A)相离 (B)相切
(C)相交 (D)相切或相交【解析】选B.作CD⊥AB于点D.
∵∠B=30°,BC=4 cm,
∴CD=2 cm,等于半径.
∴AB与⊙C相切.3.如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),
当该圆向上平移______个单位时,它与x轴相切.【解析】设圆的半径为r,圆心到直线的距离为d,要使圆与x轴相
切,必须使d=r.∵此时d=3,∴圆向上平移1或5个单位时,它与x轴
相切.
答案:1或54.如图,在矩形ABCD中,AB=6,BC=4,⊙O是以AB为直径的圆,试说明直线DC与⊙O的位置关系.
【解析】∵矩形ABCD中,BC=4,
∴圆心到CD的距离为4.∵AB为直径,AB=6,
∴半径是3.∵4>3,∴直线DC与⊙O相离.
