2020春华师版九下数学 27.2.3切线第1课时课件(35张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.2.3切线第1课时课件(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 834.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:13:42 | ||
图片预览









文档简介
课件35张PPT。第1课时 1.你能归纳切线的判定定理吗?
答:经过半径_____并且_____这条半径的_____是圆的切线.
【点拨】这个定理包含了两个条件:①直线经过半径的外端
点;②直线垂直于这条半径.这两个条件缺一不可. 外端垂直直线2.试说出判定一条直线是圆的切线的3种方法.
答:___________________________________
_______________________________________
_________________________________________________.
3.你能说出圆的切线的性质吗?
答:圆的切线_____于过_____的半径. ①与圆有唯一公共点的直线是圆的切线;②与圆心的距离等于半径的直线是圆的切线;③经过半径外端并且垂直于这条半径的直线是圆的切线垂直切点【预习思考】圆的切线的判定定理中的“半径”改为“直径”
可以吗?
提示:可以. 切线的判定
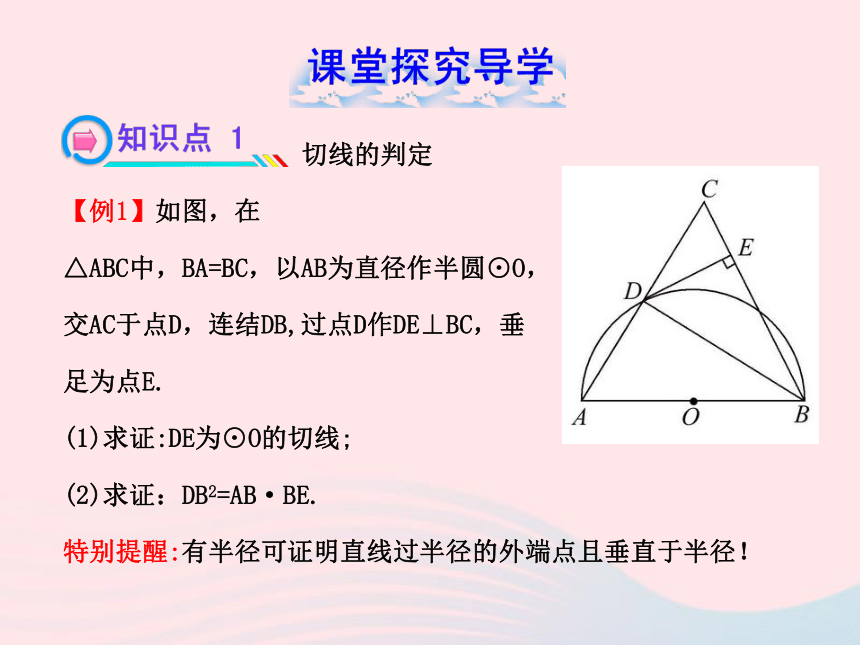
【例1】如图,在
△ABC中,BA=BC,以AB为直径作半圆⊙O,
交AC于点D,连结DB,过点D作DE⊥BC,垂
足为点E.
(1)求证:DE为⊙O的切线;
(2)求证:DB2=AB·BE.
特别提醒:有半径可证明直线过半径的外端点且垂直于半径! 【规范解答】(1)连结OD,………………………………1分
∵AB=BC,
∴∠BAC=∠BCA,…………………………………………2分
∵OA=OD,∴∠BAC=∠ODA,………………………………3分
∴∠BCA=∠ODA.…………………………………………4分
∵DE⊥BC,∴∠DEC=90°,在直角三角形DCE中,
∠BCA+∠CDE=90°,
∴∠ODA+∠CDE=90°,即∠ODE=90°.…………………5分
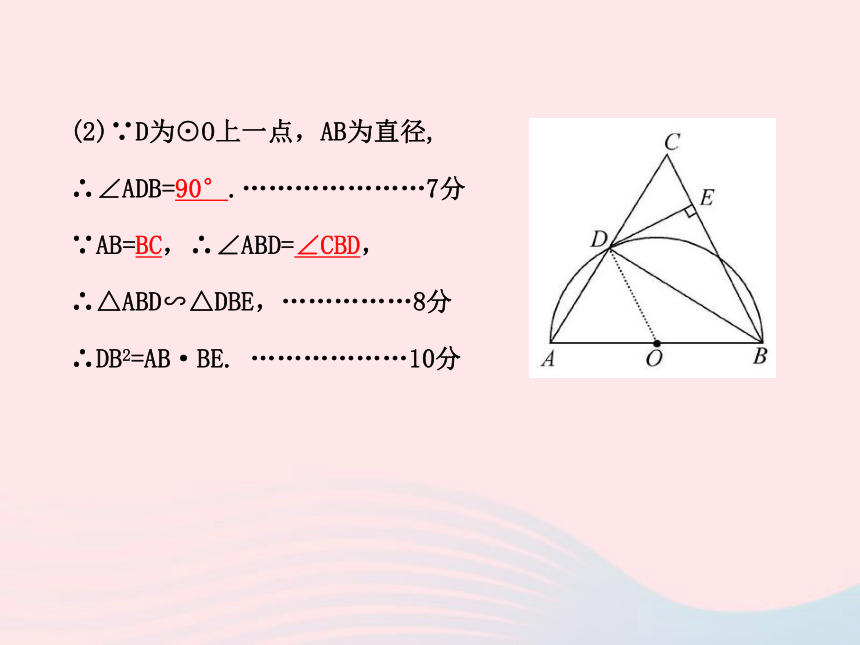
∴DE是⊙O的切线.………………………………………6分(2)∵D为⊙O上一点,AB为直径,
∴∠ADB=90°.…………………7分
∵AB=BC,∴∠ABD=∠CBD,
∴△ABD∽△DBE,……………8分
∴DB2=AB·BE. ………………10分【规律总结】
证明直线与圆相切时作辅助线的两种方法
1.“连半径,证垂直”:已明确直线和圆有公共点,辅助线的作
法是连结圆心和公共点,即得“半径”,再证“直线与半径垂
直”.
2.“作垂直,证半径”:不明确直线和圆有公共点,辅助线的作
法是过圆心作直线的垂线,再证“圆心到直线的距离等于半
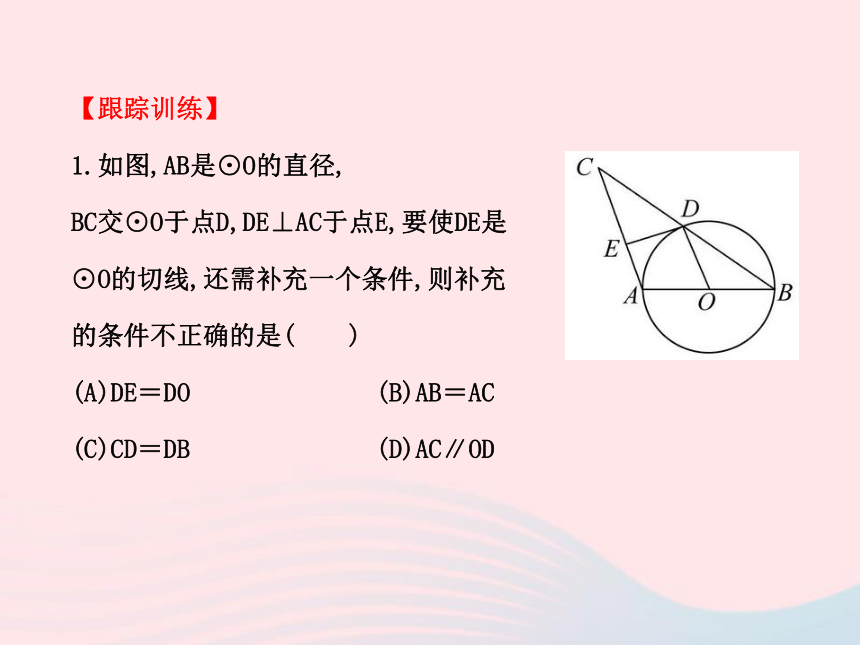
径”.【跟踪训练】
1.如图,AB是⊙O的直径,
BC交⊙O于点D,DE⊥AC于点E,要使DE是
⊙O的切线,还需补充一个条件,则补充
的条件不正确的是( )
(A)DE=DO (B)AB=AC
(C)CD=DB (D)AC∥OD【解析】选A.由于D是圆上一点,所以要说明DE是切线,只需证明
OD⊥DE即可,又因为DE⊥AC,所以当AC∥OD时,可得OD⊥DE,进一
步当CD=DB时,即D为BC的中点,而O为AB的中点,所以OD∥AC,当
AB=AC时,连结AD,因为AB是直径,所以AD⊥BC,所以CD=DB,因此
B、C、D条件均可以说明DE是⊙O的切线.2.矩形的两邻边长分别为2.5和5,若以较长一边为直径作半圆,
则矩形的各边与半圆相切的线段最多有( )
(A)0条 (B)1条
(C)2条 (D)3条
【解析】选D.以较长的边为直径作圆,半径正好与另一边相等,
所以如图可知,与半圆相切的线段有3条. 3.以等腰三角形顶角的顶点为圆心,顶角的平分线为半径的圆与
底边________.
【解析】根据等腰三角形的性质可得等腰三角形顶角平分线、
底边的中线以及底边上的高重合,以及切线的判定(经过半径的
外端且垂直于这条半径的直线是圆的切线)可得到以等腰三角形
顶角的顶点为圆心,顶角的平分线为半径的圆必与底边相切.
答案:相切4.已知:如图所示,在△AOB中,OC⊥AB于C,∠AOC=∠B,AC=16,
BC=4,⊙O的半径等于8.求证:AB是⊙O的切线. 【证明】∵OC⊥AB于C,
∴∠ACO=∠OCB=90°.
∵∠AOC=∠B,
∴△AOC∽△OBC.
∴
∵AC=16,BC=4,
∴OC=8=⊙O的半径.
∴AB是⊙O的切线. 切线的性质
【例2】如图,AB为⊙O
的直径,BC为⊙O的切线,AC交⊙O于点E,
D为AC上一点,∠AOD=∠C.
(1)求证:OD⊥AC;
(2)若AE=8,tan A= ,求OD的长.【解题探究】(1)①试说出∠A与∠C的关系.
答:∵BC是⊙O的切线,AB为⊙O的直径,
∴∠ABC=90°,∴∠A+∠C=90°,
即∠A与∠C互余.
②由①知∠A+∠C=90°,又∠AOD=∠C,所以∠A+∠AOD=90°,即
∠ADO=90°,所以OD⊥AC.(2)①因为OD⊥AE,O为圆心,AE=8, 依据垂径定理可得:
D为AE的中点,所以AD=4.
②因为tan A= 所以OD=AD·tan A,
所以OD=【规律总结】
与切线有关的“五个”性质
1.切线与圆只有一个公共点;
2.切线和圆心的距离等于半径;
3.切线垂直于经过切点的半径;
4.经过圆心垂直于切线的直线必过切点;
5.经过切点垂直于切线的直线必过圆心. 【跟踪训练】
5.如图,AB为⊙O的直径,
PD切⊙O于点C,交AB的延长线于点D,且
CO=CD,则∠PCA=( )
(A)30° (B)45° (C)60° (D)67.5°
【解析】选D. PD切⊙O于点C,∴OC⊥PD,又∵OC=CD,
∴∠COD=45°,∵AO=CO,∴∠ACO=22.5°,
∴∠PCA=90°-22.5°=67.5°.【变式训练】如图,PA为⊙O的切线,A为切点.
过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点
D,与PA的延长线交于点E.
(1)求证:PB为⊙O的切线;
(2)若tan ∠ABE= ,求sin E的值.【解析】(1)连结OA,∵PA为⊙O的切线,
∴∠PAO=90°,
∵OA=OB,OP⊥AB于点C,
∴BC=CA,PB=PA,
∴△PBO≌△PAO,
∴∠PBO=∠PAO=90°,
∴PB为⊙O的切线.(2)方法一:连结AD,∵BD是直径,∠BAD=90°,
由(1)知∠BCO=90°,∴AD∥OP,
∴△ADE∽△POE,
由AD∥OC得AD=2OC ,∵tan∠ABE=
∴ 设OC=t,则BC=2t,AD=2t,
由△PBC∽△BOC,得PC=2BC=4t,OP=5t,
∴ 可设EA=2m,EP=5m,
则PA=3m,∵PA=PB,∴PB=3m,
∴sin E=方法二:连结AD,则∠BAD=90°,由(1)知∠BCO=90°,
∵AD∥OC,∴AD=2OC.
∵ 设OC=t,BC=2t,AB=4t,
由△PBC∽△BOC,得PC=2BC=4t,
∴PA=PB= 过A作AF⊥PB于点F,
则AF·PB=AB·PC,∴AF= 进而由勾股定理得PF=
∴sin E=sin ∠FAP=6.如图,已知点E在直角△ABC的斜边AB上,
以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.【解析】(1)连结OD,
∵BC是⊙O的切线,
∴OD⊥BC,又∵AC⊥BC,
∴OD∥AC,∴∠2=∠3;
∵OA=OD,∴∠1=∠3,∴∠1=∠2,
∴AD平分∠BAC;(2)∵BC与圆相切于点D.
∴∠ODB=90°,连结DE,即∠ODE+∠BDE=90°,
∵∠3+∠ODE=90°,
∴∠3=∠BDE=∠1.
又∵∠B=∠B,
∴△BED∽△BDA.
∴BD2=BE·BA,
∵BE=2,BD=4,∴BA=8,
∴AE=AB-BE=6,∴⊙O的半径为3.1.如图,已知AB是⊙O的直径,AD切⊙O于点
A, 则下列结论中不一定正确的是( )
(A)BA⊥DA (B)OC∥AE
(C)∠COE=2∠CAE (D)OD⊥AC【解析】选D.因为AD是⊙O的切线,所以BA⊥DA;由圆周角定
理得∠COE=2∠CAE,因为OA=OC,所以∠OAC=∠OCA,又因为
所以∠CAE=∠CAB,所以∠CAE=∠OCA,所以OC∥AE.2.如图,PA是⊙O的切线,切点为A,PA= ∠APO=30°,则⊙O的
半径为( )
(A)1 (B) (C)2 (D)4
【解析】选C.连结OA,∵PA是⊙O的切线,切点为A,
∴OA⊥PA,∵∠APO=30°,∴OA= 即⊙O的半径为2.3.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点
C,且∠OCB=40°,直线BC与⊙O的位置关系为________.【解析】∵∠BOC=2∠A=50°,∠OCB=40°,
∴在△OBC中,∠OBC=180°-50°-40°=90°.
∴直线BC与⊙O相切.
答案:相切4.如图,AC经过⊙O的圆心O,AB与⊙O相切于点
B,若∠A=50°,则∠C=________.
【解析】连结OB,则OB⊥AB,∴∠AOB=40°,
∴∠C=20°.
答案:20°5.如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交
BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=28°,⊙O的半径为6,求线段AD的长.(结果精确到
0.1)【解析】(1)连结OD,
∵AD平分∠BAC,∴∠BAD=∠DAC,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠ODA=∠DAC,
∴AC∥OD,
∵∠C=90°,∴∠ODC=90°,
即BC是⊙O的切线.(2)连结DE.∵∠B=28°,∴∠BAC=62°,
即∠BAD=31°,∵AE为⊙O的直径,
∴∠ADE=90°,∵OA=6,∴AE=12,
∴cos ∠DAE=
∴AD=AE·cos 31°=12×0.86≈10.3.
答:经过半径_____并且_____这条半径的_____是圆的切线.
【点拨】这个定理包含了两个条件:①直线经过半径的外端
点;②直线垂直于这条半径.这两个条件缺一不可. 外端垂直直线2.试说出判定一条直线是圆的切线的3种方法.
答:___________________________________
_______________________________________
_________________________________________________.
3.你能说出圆的切线的性质吗?
答:圆的切线_____于过_____的半径. ①与圆有唯一公共点的直线是圆的切线;②与圆心的距离等于半径的直线是圆的切线;③经过半径外端并且垂直于这条半径的直线是圆的切线垂直切点【预习思考】圆的切线的判定定理中的“半径”改为“直径”
可以吗?
提示:可以. 切线的判定
【例1】如图,在
△ABC中,BA=BC,以AB为直径作半圆⊙O,
交AC于点D,连结DB,过点D作DE⊥BC,垂
足为点E.
(1)求证:DE为⊙O的切线;
(2)求证:DB2=AB·BE.
特别提醒:有半径可证明直线过半径的外端点且垂直于半径! 【规范解答】(1)连结OD,………………………………1分
∵AB=BC,
∴∠BAC=∠BCA,…………………………………………2分
∵OA=OD,∴∠BAC=∠ODA,………………………………3分
∴∠BCA=∠ODA.…………………………………………4分
∵DE⊥BC,∴∠DEC=90°,在直角三角形DCE中,
∠BCA+∠CDE=90°,
∴∠ODA+∠CDE=90°,即∠ODE=90°.…………………5分
∴DE是⊙O的切线.………………………………………6分(2)∵D为⊙O上一点,AB为直径,
∴∠ADB=90°.…………………7分
∵AB=BC,∴∠ABD=∠CBD,
∴△ABD∽△DBE,……………8分
∴DB2=AB·BE. ………………10分【规律总结】
证明直线与圆相切时作辅助线的两种方法
1.“连半径,证垂直”:已明确直线和圆有公共点,辅助线的作
法是连结圆心和公共点,即得“半径”,再证“直线与半径垂
直”.
2.“作垂直,证半径”:不明确直线和圆有公共点,辅助线的作
法是过圆心作直线的垂线,再证“圆心到直线的距离等于半
径”.【跟踪训练】
1.如图,AB是⊙O的直径,
BC交⊙O于点D,DE⊥AC于点E,要使DE是
⊙O的切线,还需补充一个条件,则补充
的条件不正确的是( )
(A)DE=DO (B)AB=AC
(C)CD=DB (D)AC∥OD【解析】选A.由于D是圆上一点,所以要说明DE是切线,只需证明
OD⊥DE即可,又因为DE⊥AC,所以当AC∥OD时,可得OD⊥DE,进一
步当CD=DB时,即D为BC的中点,而O为AB的中点,所以OD∥AC,当
AB=AC时,连结AD,因为AB是直径,所以AD⊥BC,所以CD=DB,因此
B、C、D条件均可以说明DE是⊙O的切线.2.矩形的两邻边长分别为2.5和5,若以较长一边为直径作半圆,
则矩形的各边与半圆相切的线段最多有( )
(A)0条 (B)1条
(C)2条 (D)3条
【解析】选D.以较长的边为直径作圆,半径正好与另一边相等,
所以如图可知,与半圆相切的线段有3条. 3.以等腰三角形顶角的顶点为圆心,顶角的平分线为半径的圆与
底边________.
【解析】根据等腰三角形的性质可得等腰三角形顶角平分线、
底边的中线以及底边上的高重合,以及切线的判定(经过半径的
外端且垂直于这条半径的直线是圆的切线)可得到以等腰三角形
顶角的顶点为圆心,顶角的平分线为半径的圆必与底边相切.
答案:相切4.已知:如图所示,在△AOB中,OC⊥AB于C,∠AOC=∠B,AC=16,
BC=4,⊙O的半径等于8.求证:AB是⊙O的切线. 【证明】∵OC⊥AB于C,
∴∠ACO=∠OCB=90°.
∵∠AOC=∠B,
∴△AOC∽△OBC.
∴
∵AC=16,BC=4,
∴OC=8=⊙O的半径.
∴AB是⊙O的切线. 切线的性质
【例2】如图,AB为⊙O
的直径,BC为⊙O的切线,AC交⊙O于点E,
D为AC上一点,∠AOD=∠C.
(1)求证:OD⊥AC;
(2)若AE=8,tan A= ,求OD的长.【解题探究】(1)①试说出∠A与∠C的关系.
答:∵BC是⊙O的切线,AB为⊙O的直径,
∴∠ABC=90°,∴∠A+∠C=90°,
即∠A与∠C互余.
②由①知∠A+∠C=90°,又∠AOD=∠C,所以∠A+∠AOD=90°,即
∠ADO=90°,所以OD⊥AC.(2)①因为OD⊥AE,O为圆心,AE=8, 依据垂径定理可得:
D为AE的中点,所以AD=4.
②因为tan A= 所以OD=AD·tan A,
所以OD=【规律总结】
与切线有关的“五个”性质
1.切线与圆只有一个公共点;
2.切线和圆心的距离等于半径;
3.切线垂直于经过切点的半径;
4.经过圆心垂直于切线的直线必过切点;
5.经过切点垂直于切线的直线必过圆心. 【跟踪训练】
5.如图,AB为⊙O的直径,
PD切⊙O于点C,交AB的延长线于点D,且
CO=CD,则∠PCA=( )
(A)30° (B)45° (C)60° (D)67.5°
【解析】选D. PD切⊙O于点C,∴OC⊥PD,又∵OC=CD,
∴∠COD=45°,∵AO=CO,∴∠ACO=22.5°,
∴∠PCA=90°-22.5°=67.5°.【变式训练】如图,PA为⊙O的切线,A为切点.
过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点
D,与PA的延长线交于点E.
(1)求证:PB为⊙O的切线;
(2)若tan ∠ABE= ,求sin E的值.【解析】(1)连结OA,∵PA为⊙O的切线,
∴∠PAO=90°,
∵OA=OB,OP⊥AB于点C,
∴BC=CA,PB=PA,
∴△PBO≌△PAO,
∴∠PBO=∠PAO=90°,
∴PB为⊙O的切线.(2)方法一:连结AD,∵BD是直径,∠BAD=90°,
由(1)知∠BCO=90°,∴AD∥OP,
∴△ADE∽△POE,
由AD∥OC得AD=2OC ,∵tan∠ABE=
∴ 设OC=t,则BC=2t,AD=2t,
由△PBC∽△BOC,得PC=2BC=4t,OP=5t,
∴ 可设EA=2m,EP=5m,
则PA=3m,∵PA=PB,∴PB=3m,
∴sin E=方法二:连结AD,则∠BAD=90°,由(1)知∠BCO=90°,
∵AD∥OC,∴AD=2OC.
∵ 设OC=t,BC=2t,AB=4t,
由△PBC∽△BOC,得PC=2BC=4t,
∴PA=PB= 过A作AF⊥PB于点F,
则AF·PB=AB·PC,∴AF= 进而由勾股定理得PF=
∴sin E=sin ∠FAP=6.如图,已知点E在直角△ABC的斜边AB上,
以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.【解析】(1)连结OD,
∵BC是⊙O的切线,
∴OD⊥BC,又∵AC⊥BC,
∴OD∥AC,∴∠2=∠3;
∵OA=OD,∴∠1=∠3,∴∠1=∠2,
∴AD平分∠BAC;(2)∵BC与圆相切于点D.
∴∠ODB=90°,连结DE,即∠ODE+∠BDE=90°,
∵∠3+∠ODE=90°,
∴∠3=∠BDE=∠1.
又∵∠B=∠B,
∴△BED∽△BDA.
∴BD2=BE·BA,
∵BE=2,BD=4,∴BA=8,
∴AE=AB-BE=6,∴⊙O的半径为3.1.如图,已知AB是⊙O的直径,AD切⊙O于点
A, 则下列结论中不一定正确的是( )
(A)BA⊥DA (B)OC∥AE
(C)∠COE=2∠CAE (D)OD⊥AC【解析】选D.因为AD是⊙O的切线,所以BA⊥DA;由圆周角定
理得∠COE=2∠CAE,因为OA=OC,所以∠OAC=∠OCA,又因为
所以∠CAE=∠CAB,所以∠CAE=∠OCA,所以OC∥AE.2.如图,PA是⊙O的切线,切点为A,PA= ∠APO=30°,则⊙O的
半径为( )
(A)1 (B) (C)2 (D)4
【解析】选C.连结OA,∵PA是⊙O的切线,切点为A,
∴OA⊥PA,∵∠APO=30°,∴OA= 即⊙O的半径为2.3.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点
C,且∠OCB=40°,直线BC与⊙O的位置关系为________.【解析】∵∠BOC=2∠A=50°,∠OCB=40°,
∴在△OBC中,∠OBC=180°-50°-40°=90°.
∴直线BC与⊙O相切.
答案:相切4.如图,AC经过⊙O的圆心O,AB与⊙O相切于点
B,若∠A=50°,则∠C=________.
【解析】连结OB,则OB⊥AB,∴∠AOB=40°,
∴∠C=20°.
答案:20°5.如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交
BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=28°,⊙O的半径为6,求线段AD的长.(结果精确到
0.1)【解析】(1)连结OD,
∵AD平分∠BAC,∴∠BAD=∠DAC,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠ODA=∠DAC,
∴AC∥OD,
∵∠C=90°,∴∠ODC=90°,
即BC是⊙O的切线.(2)连结DE.∵∠B=28°,∴∠BAC=62°,
即∠BAD=31°,∵AE为⊙O的直径,
∴∠ADE=90°,∵OA=6,∴AE=12,
∴cos ∠DAE=
∴AD=AE·cos 31°=12×0.86≈10.3.
