2020春华师版九下数学 27.2.3切线第2课时课件(39张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.2.3切线第2课时课件(39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:15:04 | ||
图片预览









文档简介
课件39张PPT。第2课时1.从圆外一点可以作圆的几条切线?
答:_____.
2.什么是圆的切线长?
答:经过圆外一点作圆的切线,这点和切点之间的_____的长,叫做这点到圆的切线长.两条线段【点拨】切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.3.你能叙述切线长定理的内容吗?
答:从圆___一点可以引圆的_____切线,它们的_______相等,这
一点和圆心的连线_____这两条切线的_____.
4.三角形的内切圆
与三角形各边都_____的圆叫做三角形的_______,三角形的内切
圆的圆心叫做三角形的_____,这个三角形叫做这个圆的_______
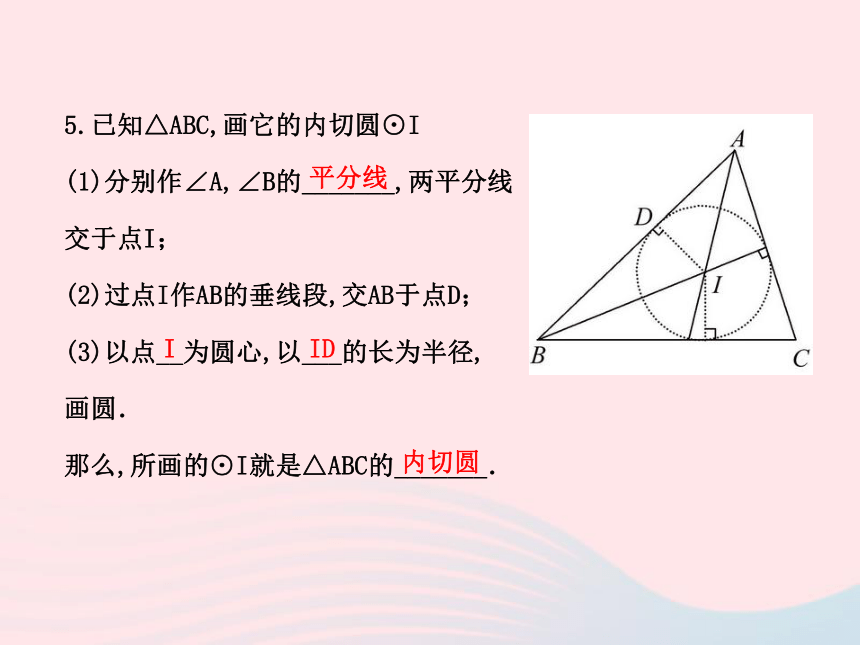
_____,三角形的内心就是三角形三个内角_______的交点.外两条切线长平分夹角相切内切圆内心外切三角形平分线5.已知△ABC,画它的内切圆⊙I
(1)分别作∠A,∠B的_______,两平分线
交于点I;
(2)过点I作AB的垂线段,交AB于点D;
(3)以点__为圆心,以___的长为半径,
画圆.
那么,所画的⊙I就是△ABC的_______.平分线IID内切圆【预习思考】经过平面上的一点作已知圆的切线,会有怎样的情形呢?
提示:(1)经过圆内一点不能作圆的切线;
(2)经过圆上一点可作圆的唯一一条切线;
(3)经过圆外一点可作圆的两条切线. 切线长定理及其应用
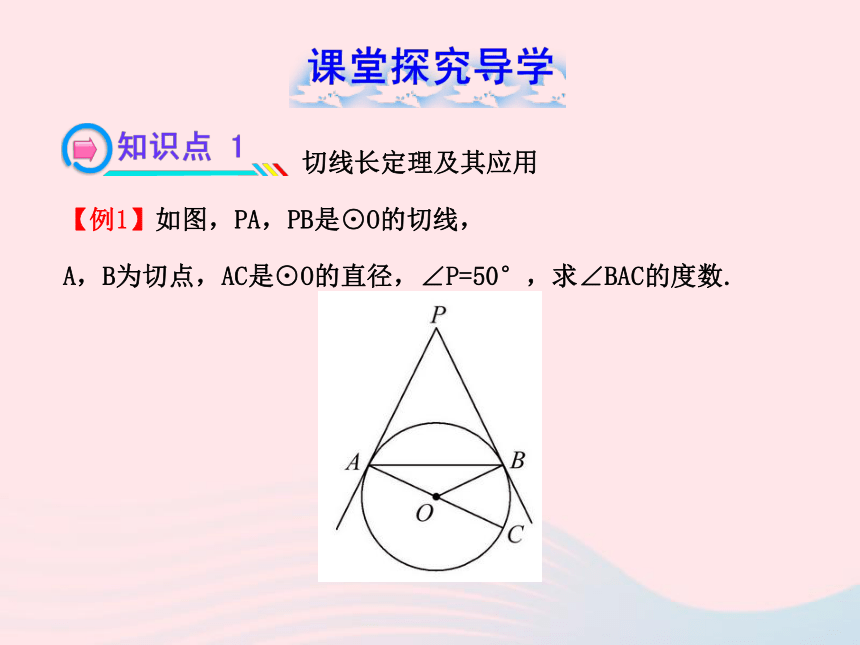
【例1】如图,PA,PB是⊙O的切线,
A,B为切点,AC是⊙O的直径,∠P=50°,求∠BAC的度数.特别提醒:PA,PB是⊙O的切线,则PA=PB.
【规范解答】∵PA,PB分别切⊙O于A,B两点,AC是⊙O的直径,
∴∠PAC=90°,PA=PB,……………………………………2分
又∵∠P=50°,∴∠PAB=∠PBA=65°,……………………4分
∴∠BAC=∠PAC-∠PAB=25°.……………………………6分【互动探究】
切线长定理主要应用在哪些方面?
提示:切线长定理体现了圆的轴对称性,它为证明线段相等、角
相等、弧相等、垂直关系等提供了理论依据.【规律总结】
有圆的两切线时引辅助线的三种方法
(1)连结圆心和两条切线的公共点,利用角平分线的性质解决问
题;(2)连结两个切点,利用等腰三角形的性质解决问题;(3)连
过切点的半径,利用直角三角形的性质及边角关系解决问题.【跟踪训练】
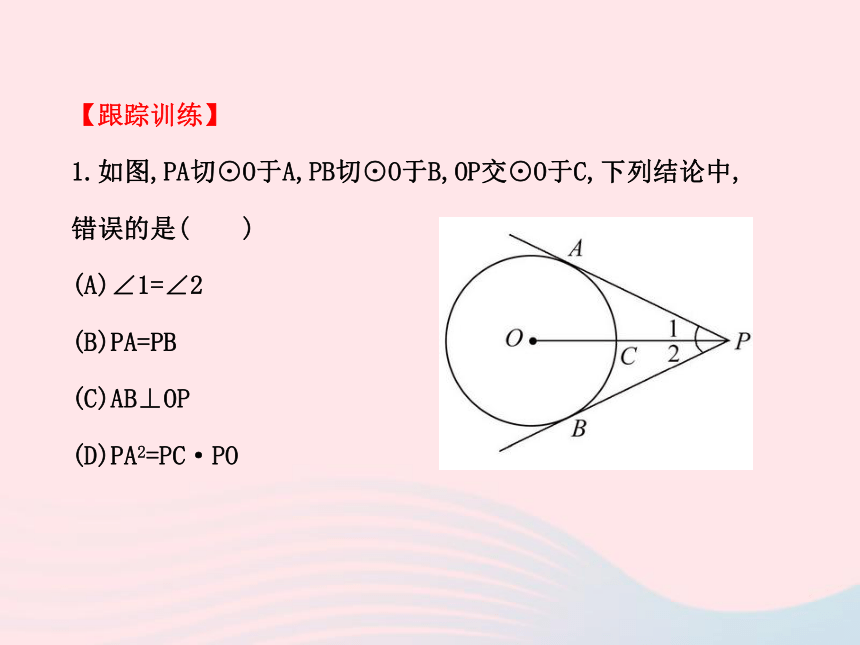
1.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,
错误的是( )
(A)∠1=∠2
(B)PA=PB
(C)AB⊥OP
(D)PA2=PC·PO【解析】选D.连结OA,OB,
∵PA切⊙O于A,PB切⊙O于B,
由切线长定理知,∠1=∠2,PA=PB,
∴△ABP是等腰三角形,
∵∠1=∠2,
∴AB⊥OP(等腰三角形三线合一),故A,B,C正确.2.如图,PA,PB,CD分别切⊙O于A,B,E,∠APB=54°,则
∠COD=( )
(A)36° (B)63° (C)126° (D)46°【解析】选B.如图,连结OA,OB,OE,
∵PA,PB,CD分别切⊙O于A,B,E,
∴∠AOC=∠EOC,同理∠BOD=∠DOE,
∴∠COD=∠COE+∠DOE=
∵∠APB=54°,∴∠AOB=126°,
∴∠COD=63°. 3.已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切
点,BC是直径.
求证:AC∥OP.【证明】方法一:如图,连结AB,
∵PA,PB分别切⊙O于A,B,
∴PA=PB,∠APO=∠BPO,
∴ OP ⊥AB.
又∵BC为⊙O的直径,∴AC⊥AB,
∴AC∥OP.方法二:连结AB,交OP于点D,
∵PA,PB分别切⊙O于A,B,
∴PA=PB,∠APO=∠BPO,∴AD=BD.
又∵BO=CO,∴OD是△ABC的中位线,
∴AC∥OP.方法三:连结AB,设OP与AB弧交于点E,
∵PA,PB分别切⊙O于A,B,
∴PA=PB,∴ OP⊥AB,
∴ ∴∠C=∠POB,∴AC∥OP. 三角形的内切圆
【例2】如图,Rt△ABC中,∠C=90°,BC=5.
⊙O内切Rt△ABC的三边AB,BC,CA于D,E,F,
半径r=2.求△ABC的周长.
【解题探究】
(1)根据切线长定理,说出图中相等的线
段有几对?
答:3对,BD=BE,CE=CF,AD=AF.(2)判断四边形OECF的形状:
答:四边形OECF是正方形,理由如下:
由(1)得BD=BE,CE=CF,AD=AF.
连结OE,OF,则OE⊥BC,OF⊥AC,又∠C=90°,
∴四边形OECF是矩形,又∵OE=OF,
∴矩形OECF是正方形. (3)试求AB和AC.
答:由(2)知CE=CF=r=2.又∵BC=5,∴BE=BD=3.
设AF=AD=x,根据勾股定理,得
(x+2)2+25=(x+3)2,解得x=10.则AC=12,AB=13.
(4)△ABC的周长是5+12+13=30.【互动探究】三角形的内切圆有几个?一个圆的外切三角形是
否只有一个?
提示:三角形的内切圆有1个,一个圆的外切三角形有无数个.【规律总结】
三角形内心的性质
(1)任意三角形的内心一定在三角形的内部;
(2)任意三角形有且只有一个内切圆;
(3)三角形的内心到三角形三边的距离相等. 【跟踪训练】
4.如图,若△ABC的三边长分别为AB=9,
BC=5,CA=6,△ABC的内切圆⊙O切AB,BC,
AC于D,E,F,则AF的长为( )
(A)5 (B)10
(C)7.5 (D)4
【解析】选A.设AF=x,根据切线长定理得AD=x,BD=BE=9-x,
CE=CF=6-x,则有9-x+6-x=5,解得x=5,即AF的长为5.5.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆
半径r=_______.【解析】如图:在Rt△ABC,∠C=90°,
AC=6,BC=8,根据勾股定理,得:
AB=10,在四边形OECF中,OE=OF,
∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形,由切线长定理,
得:AD=AF,BD=BE,CE=CF,
∴CE=CF=
即:r=
答案:26.如图,⊙O是△ABC的内切圆,与AB,BC,CA分别相切于点D,
E,F,∠DEF=45°.连结BO并延长交AC于点G,AB=4,AG=2.
(1)求∠A的度数;
(2)求⊙O的半径. 【解析】(1)连结OD,OF,
∵⊙O是△ABC的内切圆,
∴OD⊥AB,OF⊥AC.
∵∠DOF=2∠DEF=2×45°=90°,
∴四边形ADOF是矩形,
∴∠A=90°.(2)设⊙O的半径为r,由(1)知四边形ADOF是矩形,
又OD=OF,
∴四边形ADOF是正方形.
∴OD∥AC.∴△BOD∽△BGA,∴
即 解得r= ∴⊙O的半径为1.如图所示,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,
E,F,若∠DEF=52°,则∠A的度数是( )
(A)52° (B)76° (C)26° (D)128° 【解析】选B.连结OD,OF,
则∠ADO=∠AFO=90°;由圆周角定理知,
∠DOF=2∠DEF=104°,∴∠A=180°-∠DOF=76°.2.如图,在△ABC中,点P是△ABC的内心,则
∠PBC+∠PCA+∠PAB=_______°.
【解析】由于点P是△ABC的内心,则有
∠PBC+∠PCA+∠PAB
=
=
答案:903.如图,PA,PB切⊙O于A,B,过点C的切线交PA,PB于D,E,
PA=8 cm,则△PDE的周长为_____ cm.【解析】∵PA,PB切⊙O于A,B,DE切⊙O于C,
∴PA=PB=8,CD=AD,CE=BE;
∴△PDE的周长=PD+PE+CD+CE=2PA=16(cm).
答案:164.如图,PA,PB是⊙O的切线,切点分别为
A,B两点,点C在⊙O上,如果∠ACB=70°,那么∠P的度数
是_______.【解析】连结OA,OB,则∠OAP=∠OBP=90°.
又∵∠ACB=70°,∴∠AOB=140°,
在四边形APBO中,
∠P =360°-90°-90°-140°=40°.
答案:40°5.已知PA,PB,DE是⊙O的切线,切点分别为A,B,F,PO=13 cm,
⊙O的半径为5 cm,求△PDE的周长.【解析】连结OA,则OA⊥PA.
在Rt△APO中,
PO=13 cm,OA=5 cm,
根据勾股定理,
得PA=12 cm.
∵PA,PB,DE是⊙O的切线,切点分别为A,B,F,
∴PA=PB,DA=DF,EF=EB,
∴△PDE的周长=2PA=24 cm.
答:_____.
2.什么是圆的切线长?
答:经过圆外一点作圆的切线,这点和切点之间的_____的长,叫做这点到圆的切线长.两条线段【点拨】切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.3.你能叙述切线长定理的内容吗?
答:从圆___一点可以引圆的_____切线,它们的_______相等,这
一点和圆心的连线_____这两条切线的_____.
4.三角形的内切圆
与三角形各边都_____的圆叫做三角形的_______,三角形的内切
圆的圆心叫做三角形的_____,这个三角形叫做这个圆的_______
_____,三角形的内心就是三角形三个内角_______的交点.外两条切线长平分夹角相切内切圆内心外切三角形平分线5.已知△ABC,画它的内切圆⊙I
(1)分别作∠A,∠B的_______,两平分线
交于点I;
(2)过点I作AB的垂线段,交AB于点D;
(3)以点__为圆心,以___的长为半径,
画圆.
那么,所画的⊙I就是△ABC的_______.平分线IID内切圆【预习思考】经过平面上的一点作已知圆的切线,会有怎样的情形呢?
提示:(1)经过圆内一点不能作圆的切线;
(2)经过圆上一点可作圆的唯一一条切线;
(3)经过圆外一点可作圆的两条切线. 切线长定理及其应用
【例1】如图,PA,PB是⊙O的切线,
A,B为切点,AC是⊙O的直径,∠P=50°,求∠BAC的度数.特别提醒:PA,PB是⊙O的切线,则PA=PB.
【规范解答】∵PA,PB分别切⊙O于A,B两点,AC是⊙O的直径,
∴∠PAC=90°,PA=PB,……………………………………2分
又∵∠P=50°,∴∠PAB=∠PBA=65°,……………………4分
∴∠BAC=∠PAC-∠PAB=25°.……………………………6分【互动探究】
切线长定理主要应用在哪些方面?
提示:切线长定理体现了圆的轴对称性,它为证明线段相等、角
相等、弧相等、垂直关系等提供了理论依据.【规律总结】
有圆的两切线时引辅助线的三种方法
(1)连结圆心和两条切线的公共点,利用角平分线的性质解决问
题;(2)连结两个切点,利用等腰三角形的性质解决问题;(3)连
过切点的半径,利用直角三角形的性质及边角关系解决问题.【跟踪训练】
1.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,
错误的是( )
(A)∠1=∠2
(B)PA=PB
(C)AB⊥OP
(D)PA2=PC·PO【解析】选D.连结OA,OB,
∵PA切⊙O于A,PB切⊙O于B,
由切线长定理知,∠1=∠2,PA=PB,
∴△ABP是等腰三角形,
∵∠1=∠2,
∴AB⊥OP(等腰三角形三线合一),故A,B,C正确.2.如图,PA,PB,CD分别切⊙O于A,B,E,∠APB=54°,则
∠COD=( )
(A)36° (B)63° (C)126° (D)46°【解析】选B.如图,连结OA,OB,OE,
∵PA,PB,CD分别切⊙O于A,B,E,
∴∠AOC=∠EOC,同理∠BOD=∠DOE,
∴∠COD=∠COE+∠DOE=
∵∠APB=54°,∴∠AOB=126°,
∴∠COD=63°. 3.已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切
点,BC是直径.
求证:AC∥OP.【证明】方法一:如图,连结AB,
∵PA,PB分别切⊙O于A,B,
∴PA=PB,∠APO=∠BPO,
∴ OP ⊥AB.
又∵BC为⊙O的直径,∴AC⊥AB,
∴AC∥OP.方法二:连结AB,交OP于点D,
∵PA,PB分别切⊙O于A,B,
∴PA=PB,∠APO=∠BPO,∴AD=BD.
又∵BO=CO,∴OD是△ABC的中位线,
∴AC∥OP.方法三:连结AB,设OP与AB弧交于点E,
∵PA,PB分别切⊙O于A,B,
∴PA=PB,∴ OP⊥AB,
∴ ∴∠C=∠POB,∴AC∥OP. 三角形的内切圆
【例2】如图,Rt△ABC中,∠C=90°,BC=5.
⊙O内切Rt△ABC的三边AB,BC,CA于D,E,F,
半径r=2.求△ABC的周长.
【解题探究】
(1)根据切线长定理,说出图中相等的线
段有几对?
答:3对,BD=BE,CE=CF,AD=AF.(2)判断四边形OECF的形状:
答:四边形OECF是正方形,理由如下:
由(1)得BD=BE,CE=CF,AD=AF.
连结OE,OF,则OE⊥BC,OF⊥AC,又∠C=90°,
∴四边形OECF是矩形,又∵OE=OF,
∴矩形OECF是正方形. (3)试求AB和AC.
答:由(2)知CE=CF=r=2.又∵BC=5,∴BE=BD=3.
设AF=AD=x,根据勾股定理,得
(x+2)2+25=(x+3)2,解得x=10.则AC=12,AB=13.
(4)△ABC的周长是5+12+13=30.【互动探究】三角形的内切圆有几个?一个圆的外切三角形是
否只有一个?
提示:三角形的内切圆有1个,一个圆的外切三角形有无数个.【规律总结】
三角形内心的性质
(1)任意三角形的内心一定在三角形的内部;
(2)任意三角形有且只有一个内切圆;
(3)三角形的内心到三角形三边的距离相等. 【跟踪训练】
4.如图,若△ABC的三边长分别为AB=9,
BC=5,CA=6,△ABC的内切圆⊙O切AB,BC,
AC于D,E,F,则AF的长为( )
(A)5 (B)10
(C)7.5 (D)4
【解析】选A.设AF=x,根据切线长定理得AD=x,BD=BE=9-x,
CE=CF=6-x,则有9-x+6-x=5,解得x=5,即AF的长为5.5.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆
半径r=_______.【解析】如图:在Rt△ABC,∠C=90°,
AC=6,BC=8,根据勾股定理,得:
AB=10,在四边形OECF中,OE=OF,
∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形,由切线长定理,
得:AD=AF,BD=BE,CE=CF,
∴CE=CF=
即:r=
答案:26.如图,⊙O是△ABC的内切圆,与AB,BC,CA分别相切于点D,
E,F,∠DEF=45°.连结BO并延长交AC于点G,AB=4,AG=2.
(1)求∠A的度数;
(2)求⊙O的半径. 【解析】(1)连结OD,OF,
∵⊙O是△ABC的内切圆,
∴OD⊥AB,OF⊥AC.
∵∠DOF=2∠DEF=2×45°=90°,
∴四边形ADOF是矩形,
∴∠A=90°.(2)设⊙O的半径为r,由(1)知四边形ADOF是矩形,
又OD=OF,
∴四边形ADOF是正方形.
∴OD∥AC.∴△BOD∽△BGA,∴
即 解得r= ∴⊙O的半径为1.如图所示,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,
E,F,若∠DEF=52°,则∠A的度数是( )
(A)52° (B)76° (C)26° (D)128° 【解析】选B.连结OD,OF,
则∠ADO=∠AFO=90°;由圆周角定理知,
∠DOF=2∠DEF=104°,∴∠A=180°-∠DOF=76°.2.如图,在△ABC中,点P是△ABC的内心,则
∠PBC+∠PCA+∠PAB=_______°.
【解析】由于点P是△ABC的内心,则有
∠PBC+∠PCA+∠PAB
=
=
答案:903.如图,PA,PB切⊙O于A,B,过点C的切线交PA,PB于D,E,
PA=8 cm,则△PDE的周长为_____ cm.【解析】∵PA,PB切⊙O于A,B,DE切⊙O于C,
∴PA=PB=8,CD=AD,CE=BE;
∴△PDE的周长=PD+PE+CD+CE=2PA=16(cm).
答案:164.如图,PA,PB是⊙O的切线,切点分别为
A,B两点,点C在⊙O上,如果∠ACB=70°,那么∠P的度数
是_______.【解析】连结OA,OB,则∠OAP=∠OBP=90°.
又∵∠ACB=70°,∴∠AOB=140°,
在四边形APBO中,
∠P =360°-90°-90°-140°=40°.
答案:40°5.已知PA,PB,DE是⊙O的切线,切点分别为A,B,F,PO=13 cm,
⊙O的半径为5 cm,求△PDE的周长.【解析】连结OA,则OA⊥PA.
在Rt△APO中,
PO=13 cm,OA=5 cm,
根据勾股定理,
得PA=12 cm.
∵PA,PB,DE是⊙O的切线,切点分别为A,B,F,
∴PA=PB,DA=DF,EF=EB,
∴△PDE的周长=2PA=24 cm.
