2020春华师版九下数学 27.3.2圆锥的侧面积和全面积课件(24张PPT)
文档属性
| 名称 | 2020春华师版九下数学 27.3.2圆锥的侧面积和全面积课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 692.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:18:44 | ||
图片预览








文档简介
课件24张PPT。2.圆锥的侧面积和全面积1.圆锥是由一个_____和一个侧面围成的,它的_____是一个圆,侧
面是一个_____.
2.叙述圆锥的母线及圆锥的高的定义.
答:把圆锥底面圆周上的任意一点与_________的连线叫做圆锥
的母线;连结顶点与_________的线段叫做圆锥的高.底面底面曲面底面圆心圆锥顶点3.圆锥的侧面展开图是什么图形?这个图形与底面圆的周长有
什么关系?
答:圆锥的侧面展开图是_____,其弧长等于圆锥底面圆的_____.
4.圆锥侧面展开图的半径长与圆锥中的哪些线段长相等?
答:圆锥侧面展开图的半径长等于圆锥的_____长.扇形母线周长5.圆锥的侧面积与全面积:
(1)圆锥的侧面积就是弧长为圆锥底面的_____、半径为圆锥的
_________的长的_____面积,而圆锥的全面积就是它的_______
与它的_______的和.
(2)一个圆锥的母线长为a,底面半径为r,则S侧=_____,
S全=__________.周长一条母线扇形侧面积底面积πraπra+πr2【点拨】不要把圆锥的底面半径当作其侧面展开图扇形的半径,
注意区分圆锥侧面展开图中各元素与圆锥的各元素之间的对应
关系,以免在解题中出现错误.
【预习思考】圆锥的母线有多少条?都相等吗?
提示:圆锥有无数条母线,每条母线长都相等. 圆锥及其侧面展开图
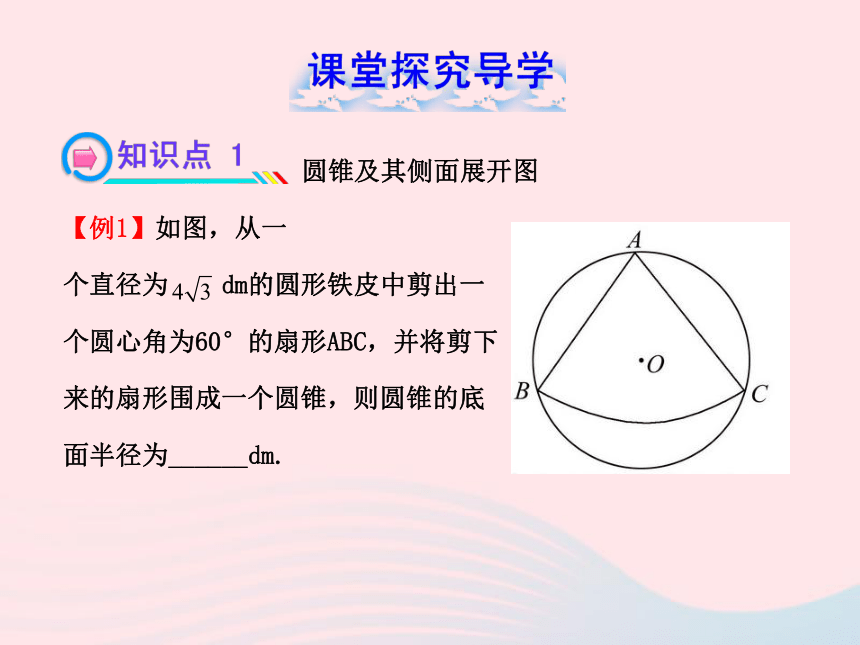
【例1】如图,从一
个直径为 dm的圆形铁皮中剪出一
个圆心角为60°的扇形ABC,并将剪下
来的扇形围成一个圆锥,则圆锥的底
面半径为______dm.【解题探究】(1)扇形ABC的半径为6dm,弧长为2πdm.
(2)围成的圆锥的底面圆的周长等于扇形ABC的弧长.
(3)设圆锥的底面半径为r,则2πr=2π,解得r=1.
故圆锥的底面半径为1dm.【规律总结】
圆锥的性质
(1)圆锥的高所在的直线就是圆锥的轴,它垂直于底面,经过底面
的圆心;
(2)圆锥的母线都相等.【跟踪训练】
1.用半径为2 cm的半圆围成一个圆锥的侧
面,这个圆锥的底面半径为( )
(A)1 cm (B)2 cm
(C)π cm (D)2π cm
【解析】选A.设围成的圆锥底面圆的半径为r,则
得r=1(cm).2.若用半径为20 cm,圆心角为240°的扇形铁皮,卷成一个圆锥
容器的侧面(接缝忽略不计),则这个圆锥容器的底面半径是
______cm.
【解析】扇形的弧长为
∴圆锥的底面半径为
答案: 圆锥面积的有关计算
【例2】(8分)在如图所示的一个机
器零件(图1)表面涂上防锈漆,
图2是其轴切面(尺寸单位:mm),
因工作需要,请你帮助计算一下
这个零件的表面积.【规范解答】
S圆锥侧=πrl=π×40×50=2 000π(mm2)…………………2分
S圆柱侧=π×80×100=8 000π(mm2)………………………4分
S底=402×π=1 600π(mm2)………………………………6分
∴S表=S圆锥侧+S圆柱侧+S底
=2 000π+8 000π+1 600π
=11 600π(mm2)……………………………………………8分【互动探究】圆锥的轴截面是什么图形?圆锥的底面半径、
高、母线之间有何关系?
提示:圆锥的轴截面是等腰三角形,圆锥的母线l和底面半径
r、圆锥的高h这三个量之间的数量关系为:r2+h2=l2.【规律总结】
圆锥的有关计算
1.圆锥侧面展开图(扇形)中的各元素与圆锥的各元素之间的关
系极为密切,即扇形的半径是圆锥的母线,扇形的弧长是圆锥底
面圆的周长.因此我们要重视空间图形与平面图形的互相转化.
2.圆锥是由一个圆和一个曲面围成的,这个曲面的展开图是一个
扇形,我们可以利用扇形的面积公式来求圆锥的侧面积,从而进
一步求出与圆锥有关的组合体和旋转体的表面积.【跟踪训练】
3.一个几何体的三视图如图所示,根据图中的相关数据求得该几
何体的侧面积为( )
(A)π (B)2π (C)3π (D)4π【解析】选B.由三视图可知,这个几何体为倒立的圆锥,如图:
所以这个圆锥的侧面积为4.底面半径为1,高为 的圆锥的侧面积
等于_______.
【解析】圆锥的母线长为2,所以其侧面展开图的面积为
π×1×2=2π.
答案:2π1.一个圆锥的底面积是侧面积的 ,则这个圆锥侧面展开图的圆
心角是( )
(A)180° (B)120° (C)90° (D)60°
【解析】选D.设圆心角为n°,母线长为R,底面半径为r,则底面
周长=2πr,底面面积=πr2,侧面面积=πrR,
∵底面积是侧面积的 ,∴R=6r,扇形的弧长
∴n=60.2.将一个圆心角是90°的扇形围成圆锥的侧面,则该圆锥的侧面
积S侧和底面积S底的关系为( )
(A)S侧=S底 (B)S侧=2S底
(C)S侧=3S底 (D)S侧=4S底
【解析】选D.设扇形的半径为R,圆锥的底面半径为r,则
因此S侧=4S底.3.已知一个圆锥的母线长为10 cm,将侧面展
开后所得扇形的圆心角是144°,则这个圆锥的底面圆的半径是
______cm.
【解析】设圆锥的底面半径为x cm,则
解得x=4.
答案:44. 一个几何体由圆锥和圆柱组成,其尺寸如
图所示,则该几何体的全面积(即表面积)为______(结果保留π).【解析】由图可知圆锥的底面直径是8,所以半径是4,因为圆
锥的高是3,根据勾股定理可得圆锥的母线长为5,根据圆锥侧
面积的计算公式可得其侧面积为 ×8π×5=20π;圆柱的侧面
积为8π×4=32π;圆柱的底面积为π×42=16π.所以,全面积
为20π+32π+16π=68π.
答案:68π5.如图,从一个半径为1 m的圆形铁皮中剪出一个圆心角为90°
的扇形,并将剪下来的扇形围成一个圆锥,则此圆锥的底面圆的
半径为多少?【解析】连结BC.依题意,线段BC是圆的直径,
∴圆锥的底面圆的半径为
面是一个_____.
2.叙述圆锥的母线及圆锥的高的定义.
答:把圆锥底面圆周上的任意一点与_________的连线叫做圆锥
的母线;连结顶点与_________的线段叫做圆锥的高.底面底面曲面底面圆心圆锥顶点3.圆锥的侧面展开图是什么图形?这个图形与底面圆的周长有
什么关系?
答:圆锥的侧面展开图是_____,其弧长等于圆锥底面圆的_____.
4.圆锥侧面展开图的半径长与圆锥中的哪些线段长相等?
答:圆锥侧面展开图的半径长等于圆锥的_____长.扇形母线周长5.圆锥的侧面积与全面积:
(1)圆锥的侧面积就是弧长为圆锥底面的_____、半径为圆锥的
_________的长的_____面积,而圆锥的全面积就是它的_______
与它的_______的和.
(2)一个圆锥的母线长为a,底面半径为r,则S侧=_____,
S全=__________.周长一条母线扇形侧面积底面积πraπra+πr2【点拨】不要把圆锥的底面半径当作其侧面展开图扇形的半径,
注意区分圆锥侧面展开图中各元素与圆锥的各元素之间的对应
关系,以免在解题中出现错误.
【预习思考】圆锥的母线有多少条?都相等吗?
提示:圆锥有无数条母线,每条母线长都相等. 圆锥及其侧面展开图
【例1】如图,从一
个直径为 dm的圆形铁皮中剪出一
个圆心角为60°的扇形ABC,并将剪下
来的扇形围成一个圆锥,则圆锥的底
面半径为______dm.【解题探究】(1)扇形ABC的半径为6dm,弧长为2πdm.
(2)围成的圆锥的底面圆的周长等于扇形ABC的弧长.
(3)设圆锥的底面半径为r,则2πr=2π,解得r=1.
故圆锥的底面半径为1dm.【规律总结】
圆锥的性质
(1)圆锥的高所在的直线就是圆锥的轴,它垂直于底面,经过底面
的圆心;
(2)圆锥的母线都相等.【跟踪训练】
1.用半径为2 cm的半圆围成一个圆锥的侧
面,这个圆锥的底面半径为( )
(A)1 cm (B)2 cm
(C)π cm (D)2π cm
【解析】选A.设围成的圆锥底面圆的半径为r,则
得r=1(cm).2.若用半径为20 cm,圆心角为240°的扇形铁皮,卷成一个圆锥
容器的侧面(接缝忽略不计),则这个圆锥容器的底面半径是
______cm.
【解析】扇形的弧长为
∴圆锥的底面半径为
答案: 圆锥面积的有关计算
【例2】(8分)在如图所示的一个机
器零件(图1)表面涂上防锈漆,
图2是其轴切面(尺寸单位:mm),
因工作需要,请你帮助计算一下
这个零件的表面积.【规范解答】
S圆锥侧=πrl=π×40×50=2 000π(mm2)…………………2分
S圆柱侧=π×80×100=8 000π(mm2)………………………4分
S底=402×π=1 600π(mm2)………………………………6分
∴S表=S圆锥侧+S圆柱侧+S底
=2 000π+8 000π+1 600π
=11 600π(mm2)……………………………………………8分【互动探究】圆锥的轴截面是什么图形?圆锥的底面半径、
高、母线之间有何关系?
提示:圆锥的轴截面是等腰三角形,圆锥的母线l和底面半径
r、圆锥的高h这三个量之间的数量关系为:r2+h2=l2.【规律总结】
圆锥的有关计算
1.圆锥侧面展开图(扇形)中的各元素与圆锥的各元素之间的关
系极为密切,即扇形的半径是圆锥的母线,扇形的弧长是圆锥底
面圆的周长.因此我们要重视空间图形与平面图形的互相转化.
2.圆锥是由一个圆和一个曲面围成的,这个曲面的展开图是一个
扇形,我们可以利用扇形的面积公式来求圆锥的侧面积,从而进
一步求出与圆锥有关的组合体和旋转体的表面积.【跟踪训练】
3.一个几何体的三视图如图所示,根据图中的相关数据求得该几
何体的侧面积为( )
(A)π (B)2π (C)3π (D)4π【解析】选B.由三视图可知,这个几何体为倒立的圆锥,如图:
所以这个圆锥的侧面积为4.底面半径为1,高为 的圆锥的侧面积
等于_______.
【解析】圆锥的母线长为2,所以其侧面展开图的面积为
π×1×2=2π.
答案:2π1.一个圆锥的底面积是侧面积的 ,则这个圆锥侧面展开图的圆
心角是( )
(A)180° (B)120° (C)90° (D)60°
【解析】选D.设圆心角为n°,母线长为R,底面半径为r,则底面
周长=2πr,底面面积=πr2,侧面面积=πrR,
∵底面积是侧面积的 ,∴R=6r,扇形的弧长
∴n=60.2.将一个圆心角是90°的扇形围成圆锥的侧面,则该圆锥的侧面
积S侧和底面积S底的关系为( )
(A)S侧=S底 (B)S侧=2S底
(C)S侧=3S底 (D)S侧=4S底
【解析】选D.设扇形的半径为R,圆锥的底面半径为r,则
因此S侧=4S底.3.已知一个圆锥的母线长为10 cm,将侧面展
开后所得扇形的圆心角是144°,则这个圆锥的底面圆的半径是
______cm.
【解析】设圆锥的底面半径为x cm,则
解得x=4.
答案:44. 一个几何体由圆锥和圆柱组成,其尺寸如
图所示,则该几何体的全面积(即表面积)为______(结果保留π).【解析】由图可知圆锥的底面直径是8,所以半径是4,因为圆
锥的高是3,根据勾股定理可得圆锥的母线长为5,根据圆锥侧
面积的计算公式可得其侧面积为 ×8π×5=20π;圆柱的侧面
积为8π×4=32π;圆柱的底面积为π×42=16π.所以,全面积
为20π+32π+16π=68π.
答案:68π5.如图,从一个半径为1 m的圆形铁皮中剪出一个圆心角为90°
的扇形,并将剪下来的扇形围成一个圆锥,则此圆锥的底面圆的
半径为多少?【解析】连结BC.依题意,线段BC是圆的直径,
∴圆锥的底面圆的半径为
