2020春华师版九下数学第27章圆 复习课件(77张PPT)
文档属性
| 名称 | 2020春华师版九下数学第27章圆 复习课件(77张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:20:11 | ||
图片预览










文档简介
课件77张PPT。第27章 单元复习课一、圆的相关概念
1.圆的定义有两种表述方式
(1)运动的观点:在一个平面内,线段OA绕它固定的一个端点O
旋转一周,另一个端点A所形成的图形叫做圆.
(2)集合的观点:圆是到定点的距离等于定长的所有点的集合.
由圆的定义可知,确定圆的因素有两个:圆心确定圆的位置,
半径确定圆的大小.2.3.与圆有关的概念较多,在辨析与圆有关的概念时,要深刻理
解每个概念的内涵与外延,熟练把握.如:
(1)等圆与同心圆:等圆是指半径相等的圆,对于位置没有限
制;同心圆是指圆心相同的圆.
(2)弦与直径:直径是一条特殊的弦,且经过圆心,它是圆中
最长的弦.直径是弦,但弦不一定是直径.(3)半圆与弧:半圆是弧,但弧不一定是半圆.
(4)对于等弧的理解,从定义来看,要求的是能够完全重合的
弧为等弧,实质上,弧有长度和度数,规定半圆的度数为
180°,劣弧的度数小于180°,优弧的度数大于180°.若两条
弧为等弧,则必须满足长度及度数都相等,二者缺一不可.4.两个概念:
(1)圆心角:顶点在圆心的角;
(2)圆周角:顶点在圆上,并且两边都与圆相交的角.
圆心角的顶点在圆的内部,所以其边一定与圆相交;圆周角
必须满足两个条件,二者缺一不可.5.经过三角形三个顶点的圆叫做这个三角形的外接圆,这个三
角形叫做这个圆的内接三角形,三角形外接圆的圆心叫做这个
三角形的外心.
(1)一个三角形有且只有一个外接圆,但是一个圆有无数个内
接三角形.
(2)三角形的外心就是三角形三条边的垂直平分线的交点,到
三角形三顶点的距离相等,等于外接圆的半径.
(3)锐角三角形的外心在三角形的内部,直角三角形的外心是
斜边的中点,钝角三角形的外心在三角形的外部.6.与三角形各边都相切的圆叫做这个三角形的内切圆.三角形
的内切圆的圆心叫做这个三角形的内心,这个三角形叫做这个
圆的外切三角形.
(1)一个三角形有且只有一个内切圆,但是一个圆有无数个外
切三角形;
(2)三角形的内心是三角形三条角平分线的交点,它到三角形
三边的距离相等;
(3)与三角形内心有关的证明或计算,往往连结顶点与内心,
构造角平分线,应用角平分线的性质来证明或计算.7.圆的切线上某一点与切点之间的线段的长,叫做这点到圆的
切线长.
切线和切线长是两个不同的概念,切线是直线,不可度量,切
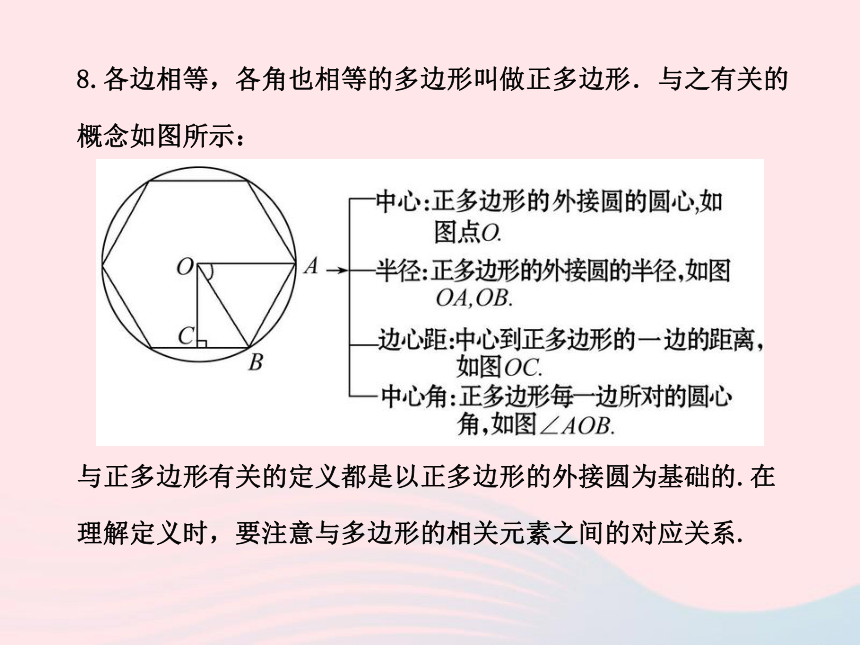
线长是切线上一条线段的长,可以度量.8.各边相等,各角也相等的多边形叫做正多边形.与之有关的
概念如图所示:
与正多边形有关的定义都是以正多边形的外接圆为基础的.在
理解定义时,要注意与多边形的相关元素之间的对应关系.二、圆的相关性质、判定及定理
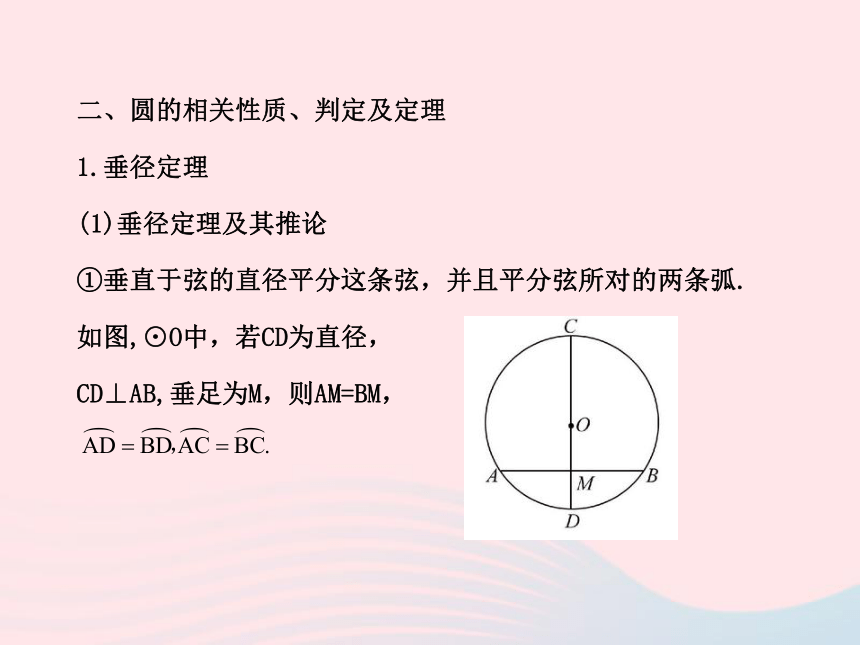
1.垂径定理
(1)垂径定理及其推论
①垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
如图,⊙O中,若CD为直径,
CD⊥AB,垂足为M,则AM=BM,②平分弦(不是直径)的直径垂直于这条弦,并且平分弦所对的
弧;平分弧的直径垂直平分这条弧所对的弦.
如图,⊙O中,若AM=BM(AB不是直径),CD为直径,则AB⊥CD,
(2)理解垂径定理要注意以下问题:
①定理中的“垂径”可以是直径、半径或过圆心的直线,其本
质是“经过圆心”.②定理中的“弦”是直径时,结论仍然成立.
③垂径定理可以这样理解:一条直线,如果它具备两条:
a经过圆心;
b垂直于圆的一条弦.那么这条直线就具有另外三个性质:
a平分弦;
b平分弦所对的劣弧;
c平分弦所对的优弧.(3)垂径定理的其他推论
垂径定理成立的基础是圆的轴对称性,垂径定理及其推论可以
概括为:一条直线,如果它满足:①经过圆心;②垂直于圆的一
条弦;③平分弦;④平分弦所对的劣弧;⑤平分弦所对的优弧.
这五条中的任意两条,则必然具备其余三条,简称“知二推
三”.
注:在垂径定理的推论中,对被平分的弦不是直径的要求是不
可去掉的,在圆中任意的两条直径都是互相平分的,但是它们
不一定垂直.(4)垂径定理的应用
垂径定理是证明线段相等、角相等、垂直
关系、弧相等的重要依据,同时也为圆的
有关计算提供了方法和依据.
①应用垂径定理证明时,一般是过圆心作
弦的垂线,构造线段或弧相等.若有弦的中点,则连结圆心及弦
的中点,构造垂直关系.②与垂径定理有关的计算,一般是利用弦长的一半、弦心距、
半径所构成的直角三角形结合勾股定理及方程的思想求解.如图,常用的关系式为:r2= +d2,r=d+h等.若已知弦长a和弓形
的高h,则需要构建关于r的方程,利用方程的思想来解决.
③确定弧所在圆的圆心的方法,根据弦的垂直平分线经过圆
心,在弧上任意作两条弦,两弦的垂直平分线的交点就是弧所
在圆的圆心.
④应用垂径定理解决实际问题,关键是根据实际问题抽象出几
何模型,利用垂径定理来解决问题.2.弧、弦、圆心角、圆周角的关系
(1)弧、弦、圆心角之间的关系
在同圆或等圆中,有三组量:两个圆心角、两条弧、两条弦,
只要有一组量对应相等,它们所对应的其余各组量也都相等.
此定理成立的基础是圆的旋转不变性.在应用上述关系解决问题
时,可根据需要选取有关部分;“在同圆或等圆中”这一条件
不能漏掉,如在不同的圆中,相等的圆心角所对的弦及弧不一
定相等,但是相等的弧所对的圆心角一定相等,因为等弧只有
在同圆或等圆中才有可能存在.(2)圆周角定理及其推论
①在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该
弧所对的圆心角的一半;相等的圆周角所对的弧相等.
②半圆或直径所对的圆周角都相等,都等于90°(直角).
③90°的圆周角所对的弦是直径.
(3)圆内接四边形的性质:圆内接四边形的对角互补.3.切线的判定及性质
(1)切线的性质:圆的切线垂直于经过切点的半径.
①切线的性质可以作如下拓展:a切线和圆只有一个公共点;b
切线和圆心的距离等于圆的半径;c经过圆心且垂直于切线的直
线必过切点;d经过切点且垂直于切线的直线必过圆心.
②有圆的切线时,辅助线的作法一般是连结切点和圆心,构造
垂直关系来解题.(2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线
长相等,这一点和圆心的连线平分两条切线的夹角.
切线长定理能把许多圆的知识串联起来,并能找出一些规律性
的东西,便于应用,也有利于开阔思路.
如图,PA,PB分别切⊙O于A,B两点,直线OP交⊙O于D,E,
交弦AB于C,则:①由切线长定理得PA=PB,∠3=∠4.
②由等腰三角形三线合一得PC⊥AB,AC=BC.
③由垂径定理得:
④由切线性质定理得:OA⊥AP,OB⊥BP.
⑤连结AD,BD,由AD,BD分别平分∠PAB,∠PBA得:D为△ABP
的内心.
⑥∠1=∠2=∠3=∠4,∠5=∠6=∠7=∠8.(3)圆切线的判定方法
①定义:和圆只有一个公共点的直线是圆的切线.
②数量关系:和圆心距离等于半径的直线是圆的切线.
③判定定理:经过半径的外端且垂直于这条半径的直线是圆的
切线.
应用切线的判定定理证明直线与圆相切时,常用的辅助线的作
法为:(1)若已知直线与圆有公共点,则连结圆心和公共点证明
垂直,即“连半径,证垂直”;(2)若直线与圆的公共点没有确定,则过圆心作直线的垂线,证明圆心到直线的距离等于圆的
半径,即“作垂直,证等径”.
(4)直角三角形内切圆的半径与三边的关系
设直角三角形的两直角边为a,b,斜边为c,内切圆的半径为
r,则有 ,或 (由面积法得到).4.定理的应用
(1)在同圆或等圆中,证两弦相等时,常用的方法是找这两弦所
对的弧、圆心角、圆周角相等.同样,证明弧相等时,则考虑弧
所对的弦及有关的角之间存在的关系.
(2)利用圆周角定理解决问题时,常进行两种转化:一是利用同
弧所对的圆周角相等,进行角与角之间的转化;二是将圆周角
相等的问题转化为弦相等或弧相等或圆心角相等的问题.(3)把圆中的直径与90°的圆周角联系在一起,当题目中有直径
这一条件时,辅助线的作法一般是构造直径所对的圆周角是直
角,综合勾股定理等知识来解题.没有直径时常通过添加辅助线
作直径,创造条件,再利用圆周角的性质解题.
(4)若出现圆内接四边形,则利用其对角互补解决问题.
注:(1)在进行相关命题的判断时,易忽视“在同圆或等圆中”
这个条件而造成误判;
(2)与圆周角有关的问题常因图形不确定而产生多解的情况,此
时易忽视分情况进行讨论而导致丢解的错误.5.相切两圆的性质
如果两圆相切,那么切点一定在连心线上.
(1)要正确区别连心线和圆心距:连心线是通过不同心的两个圆
的圆心的一条直线,而圆心距是指两个圆心之间的线段的长度.
显然,两个圆的圆心的连线(线段)一定在连心线(直线)上.
(2)“相切两圆的连心线经过切点” ,也可理解为“相切两圆
的圆心、切点在同一条直线上” ,或“经过相切两圆的切点和
一个圆的圆心的直线必经过另一个圆的圆心” .(3)两圆相切时,连心线是常见的一条辅助线,使用连心线时要
注意:连心线是直线而不是线段;有时也用圆心距作辅助线.
注:由两圆相切的位置关系判断数量关系时,易忽视存在两种
情况而造成漏解.三、圆中的位置关系
1.点与圆的位置关系的判断方法
方法一:确定点和圆的位置关系,就是确定该点到圆心的距离
与半径的大小关系.先求出点到圆心的距离,并与圆的半径作比
较,如果P是圆所在平面内的一点,d表示点到圆心的距离,r表
示圆的半径,那么:
d<r ?P在圆内;d=r ?P在圆上;d>r ?P在圆外.方法二:利用圆内角、圆周角、圆外角三种角之间的大小来判
断,如果AB是⊙O的一条弦,点Q是⊙O上的一点,P点、Q点在直
线AB的同旁(如图),则有:
(1)∠APB>∠AQB?点P在圆内;
(2)∠APB=∠AQB?点P在圆上;
(3)∠APB<∠AQB?点P在圆外.2.直线与圆的位置关系
判断直线和圆的位置关系既可转化为直线和圆的交点的个数,
又可转化为点(圆心)到直线的距离与半径的大小关系.若⊙O的
半径为r,圆心O到直线l的距离为d,则具体情况如下表:3.圆和圆的位置关系
圆和圆的位置关系可以分为三大类:相离、相切、相交.相离包括外离与内含两种情况,相切包括外切与内切,在理解它们
时,要注意每个圆上的点相对于另一个圆的位置关系.
(1)圆和圆的位置关系,不但考虑了数(两圆公共点的个数),而
且考虑了形(两圆的位置关系),两圆的五种位置关系按公共点
的个数可分为0,1,2三大类.
(2)两圆外切和两圆内切,统一称为两圆相切,唯一的公共点称
为切点.
(3)具有内切或内含关系的两个圆的半径R与r不可能相等,即具
有内切或内含关系的两圆不可能为等圆,否则,这两个圆重合.四、圆中的相关计算
1.正多边形的有关计算
正n边形的半径和边心距把正n边形分成
2n个全等的直角三角形,由于这些直角
三角形的斜边都是正n边形的外接圆的半
径R,一条直角边是正n边形的边心距rn,
另一条直角边是正n边形的边长an的一半,
一个锐角是正n边形中心角αn的一半,即 另一个锐角为一个内角的一半,即 所以,根据上
面定理就可以把正n边形的有关计算归结为解直角三角形问题.
这样就把正n边形的计算问题转化为解直角三角形的问题.
计算公式:
(1)正n边形每个内角的度数:
(2)正n边形的中心角的度数:
(3)正n边形的每个外角的度数:(4)正n边形的对角线的条数:
注:(1)计算时易记错公式导致错误.
(2)易将正n边形的边心距和半径混淆.
2.弧长及扇形面积公式(半径为R的圆中)
(1)弧长:n°的圆心角所对的弧长
(2)扇形的面积:
①n°的圆心角所对的扇形面积
②弧长为l的扇形的面积弧是圆的一部分,扇形是圆面的一部分,所以在半径为R的圆
中,360°的圆心角所对的弧长就是圆的周长2πR,所以1°的
圆心角所对的弧长为 圆心角为1°的扇形的面积为
由此可以得到弧长和扇形的面积计算公式.
在公式中,n,180,360应理解为1°的倍数,计算时都不带单
位.扇形的第二个面积公式,与三角形的面积公式类似,为了便
于记忆,可以把扇形理解成一个曲边的等腰三角形.两个公式在
计算时要根据条件灵活选用.五、圆锥的侧面展开图与侧面积计算
圆锥的侧面展开图是一个扇形,这个扇形的半径是圆锥侧面的
母线、圆心是圆锥的顶点、弧长是圆锥底面圆的周长.
圆锥侧面积是扇形面积.
如果设扇形的半径为l,弧长为c,圆心角
为n°(如图),则它们之间有如下关系:同时,如果设圆锥底面半径为r,周长为c,侧面母线长为l,那么它的侧面积是:
圆锥的全面积为:πrl+πr2. 圆的对称性
【相关链接】
圆既是轴对称图形,又是中心对称图形.与之相关的定理有垂径
定理及其推论,圆心角、弧、弦之间的关系.它们是计算线段的
长度,证明线段相等、角相等、弧相等的重要依据.应用垂径定
理时,常作圆心到弦的垂线段,与半径、弦长的一半构成直角三
角形,结合勾股定理计算或证明.【例1】如图,DE是⊙O的直径,弦AB⊥DE,垂足
为C,若AB=6,CE=1,则OC=______,CD=______.【思路点拨】
【自主解答】如图连结OA,设⊙O的半径为R,
由垂径定理得AC= AB=3, OC=R-1,
根据勾股定理, AC2+OC2=OA2得
32+(R-1)2=R2,解得R=5, ∴OC=4,CD=9.
答案:4 9 圆周角定理及其推论
【相关链接】
圆周角定理提供了与圆有关的角的转化方法.圆周角与圆心角
的关系、同弧或等弧所对的圆周角相等是证明角相等的重要依
据,进而也可计算或证明有关线段的问题.在题目中,若有直径,
常作直径所对的圆周角,构造直角三角形,利用解直角三角形的
知识解决问题.【例2】如图,点A,B,C,D都在⊙O上,
OC⊥AB,∠ADC=30°,求∠BOC的度数. 【思路点拨】
【自主解答】∵点A,B,C,D都在⊙O上,OC⊥AB,
∵∠ADC=30°,
∴∠AOC=∠BOC=2∠ADC=60°,
∴∠BOC的度数为60°. 切线的性质与判定、切线长定理
【相关链接】
(1)在证明直线与圆的位置关系时,若有公共点,则连结公共点
与圆心,证半径与直线垂直;若直线与圆的公共点未知时,可作
出圆心到直线的垂线段,证明圆心到直线的距离和半径相等,从
而判定直线和圆相切;
(2)利用切线的性质时,常连结切点和圆心,则半径与切线垂
直;切线长定理与切线的性质定理的综合应用往往是证明线段
相等、角相等、弧相等及垂直关系的重要依据.【例3】如图,点A,E是半圆周上的三等分
点,直径BC=2,AD⊥BC,垂足为D,连结BE交AD于F,过A作
AG∥BE交BC于G.
(1)判断直线AG与⊙O的位置关系,并说明理由.
(2)求线段AF的长.【思路点拨】(1)
(2)
【自主解答】(1)AG与⊙O相切.
证明:连结OA,
∵点A,E是半圆周上的三等分点,
∴点A是 的中点,
∴OA⊥BE.
又∵AG∥BE,
∴OA⊥AG.
∴AG与⊙O相切.(2)∵点A,E是半圆周上的三等分点,
∴∠AOB=∠AOE=∠EOC=60°.
又OA=OB,
∴△ABO为正三角形.
又AD⊥OB,OB=1,
∴BD=OD= , AD= .
又∠EBC= =30°,
在Rt△FBD中, FD=BD·tan ∠EBC=BD ·tan 30°= 圆和圆的位置关系
【相关链接】
圆和圆的位置关系重点考查两圆相切和相交两种情况,其中相切
又分为外切和内切,在解题时常常因考虑不全而漏解.相交时常
添加的辅助线是两圆的公共弦,把两圆中的角或线段联系起来,
起到了桥梁的作用.【例4】如果两圆的半径分别为6和4,圆心距
为10,那么这两圆的位置关系是( )
(A)内含 (B)内切 (C)相交 (D)外切
【思路点拨】
【自主解答】选D.∵两圆的半径分别为4和6,圆心距为10,又
∵4+6=10,∴这两圆的位置关系是外切. 弧长和扇形、圆锥面积的相关计算
【相关链接】
(1)弧长和扇形面积的计算,关键是寻求所在圆的半径及弧所对
的圆心角;
(2)圆锥的侧面展开图是一个扇形,扇形的弧长为圆锥底面圆的
周长,半径为圆锥的母线;圆锥的高、母线和底面半径构成一个
直角三角形;
(3)计算不规则图形的面积时,常转化为规则图形
面积的和或差来解决.【例5】如图,Rt△ABC
中,∠ACB=90°,AC=BC= , 若把Rt△ABC
绕边AB所在直线旋转一周则所得的几何体
的表面积为( )
(A)4π (B)
(C)8π (D) 【思路点拨】
【自主解答】选D.由三角形绕斜边旋转后得到的,求表面积,实
际是两个圆锥的侧面积之和,一个圆锥的母线是原直角三角形的
一条直角边,半径是斜边的中线,等于2,圆锥的侧面是个扇形,其
弧长为圆锥底面圆的周长,即4π,其半径是圆锥的母线长,即AC
的长,然后再利用扇形的面积公式S= ×弧长×半径
则两个的和为【命题揭秘】
圆是数学的重点之一,也是中考的热点,纵观近几年中考,题型
包含选择题、填空题、解答题.在填空题、选择题里常常考的
是单独的一个知识点,如:圆周角、点与圆的位置关系、两圆
的位置关系、弧长的计算等,解答题是稍微综合点的,常常是几
个知识点综合起来考.常考的有:切线的性质与判定,垂径定理
或圆周角定理结合勾股定理或相似三角形来考.1.已知两圆的直径分别为2 cm和4 cm,圆心
距为3 cm,则这两个圆的位置关系是( )
(A)相交 (B)外切
(C)外离 (D)内含
【解析】选B.两圆半径分别为1 cm和2 cm,圆心距等于两圆半径
之和,所以这两个圆外切.2.如图所示,直线
CD与以线段AB为直径的圆相切于点D
并交BA的延长线于点C,且AB=2,AD=
1,P点在切线CD上移动.当∠APB的度
数最大时,∠ABP的度数为( )
(A)15° (B)30°
(C)60° (D)90°【解析】选B.当P点运动到点D时,此时∠APB=∠ADB为最大角.在直角三角形ABD中,AB=2,AD=1,所以∠ABP=30°.3.如图,AB是⊙O的
直径,点E为BC的中点,AB=4,∠BED
=120°,则图中阴影部分的面积之和
为( )
(A)1 (B)
(C) (D)【解析】选C.连结AE,
∵AB是直径,
∴∠AEB=90°,
又∵∠BED=120°,
∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD,
∴△AOD是等边三角形,∴∠A=60°,∵点E为BC的中点,∠AED=90°,
∴AB=AC,
∴△ABC是等边三角形.
△EDC是等边三角形,边长是2.
∴∠BOE=∠EOD=60°,
∴ 和弦BE围成的部分的面积= 和弦DE围成的部分的面积.
∴阴影部分的面积=
故选C.4.用圆心角为120°,半径为6 cm的扇形做成
一个无底的圆锥侧面,则此圆锥的底面半径为_____cm.
【解析】把n=120°,r=6代入 得l=4π;所以圆锥的底
面周长为4π,
则4π=2Rπ,所以R=2.
答案:25.母线长为3,底面圆的直径为2的圆锥的侧面
积为______.
【解析】
答案:3π6.如图,在直角坐标
系中,四边形OABC是直角梯形,BC∥OA,
⊙P分别与OA,OC,BC相切于点E,D,B,
与AB交于点F.已知A(2,0),B(1,2),
则tan∠FDE=______.【解析】连结BE.∵BC∥OA,∴BE为⊙P的直径.由A(2,0),
B(1,2),得BC=1,AO=2,BE=2,∴AE=2-1=1.在直角三角形ABE
中,tan∠FDE=tan∠ABE=
答案:7.如图,已知AD为⊙O的直径,B为AD延长线
上一点,BC与⊙O切于C点,∠A=30°.
求证:(1)BD=CD;
(2)△AOC≌△CDB.【证明】(1)∵AD为⊙O的直径,∴ ∠ACD=90°,
又∵∠A=30°,OA=OC=OD,
∴∠ACO=30°,∠ODC=∠OCD=60°,
又∵BC与⊙O切于C,
∴∠OCB=90°,∴∠BCD=30°,∴∠B=30°,
∴∠BCD=∠B,∴BD=CD.
(2)∵∠A=∠ACO=∠BCD=∠B=30°,
∴AC=BC,∴△AOC≌△BDC.8.如图,D为⊙O上一点,点C在直径BA的延长
线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=6,
tan∠CDA= ,求BE的长.【解析】(1)如图,连结OD,
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又AB是⊙O的直径,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°即∠CDO=90°,
∴CD是⊙O的切线.(2)由tan∠CDA=tan∠ABD=
∵∠C=∠C,∠CDA=∠CBD,
∴△CAD∽△CDB,
∵BC=6,∴CD=4。
∵CE,BE是⊙O的切线,
∴BE=DE,BE⊥BC,
∴BE2+BC2=EC2即(4+BE)2=62+BE2,解得BE=【拓展思维】
圆中常见辅助线口诀
半径与弦长计算,弦心距来中间站.
圆上若有一切线,切点圆心半径连.
切线长度的计算,勾股定理最方便.
要想证明是切线,半径垂线仔细辨.
是直径,成半圆,想成直角径连弦.
弧有中点圆心连,垂径定理要记全.
圆周角边两条弦,直径和弦端点连.弦切角边切线弦,同弧对角等找完.
要想作个外接圆,各边作出中垂线.
还要作个内接圆,内角平分线梦圆.
如果遇到相交圆,不要忘作公共弦.
内外相切的两圆,经过切点公切线.
若是添上连心线,切点肯定在上面.
要作等角添个圆,证明题目少困难.9.如图,△ABC内
接于⊙O,直径BD交AC于E,过O作FG
⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OF·DE=OE·2OH;
(2)若⊙O的半径为12,且OE∶OF∶OD
=2∶3∶6,求阴影部分的面积.
(结果保留根号)【解析】(1)∵BD是直径,∴∠DAB=90°.
∵FG⊥AB,∴DA∥FO.
∴∠EOF=∠EDA,∠EFO=∠EAD.
∴△FOE∽△ADE.
即OF·DE=OE·AD.
∵O是BD的中点,DA∥OH,
∴AD=2OH.
∴OF·DE=OE·2OH.(2)∵⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,
∴OE=4,ED=8,OF=6.
代入(1)结论,得AD=12. ∴OH=6.
在Rt△ABC中,OB=2OH,∴∠BOH=60°.
∴BH=BO·sin60°=
∴S阴影=S扇形GOB-S△OHB
1.圆的定义有两种表述方式
(1)运动的观点:在一个平面内,线段OA绕它固定的一个端点O
旋转一周,另一个端点A所形成的图形叫做圆.
(2)集合的观点:圆是到定点的距离等于定长的所有点的集合.
由圆的定义可知,确定圆的因素有两个:圆心确定圆的位置,
半径确定圆的大小.2.3.与圆有关的概念较多,在辨析与圆有关的概念时,要深刻理
解每个概念的内涵与外延,熟练把握.如:
(1)等圆与同心圆:等圆是指半径相等的圆,对于位置没有限
制;同心圆是指圆心相同的圆.
(2)弦与直径:直径是一条特殊的弦,且经过圆心,它是圆中
最长的弦.直径是弦,但弦不一定是直径.(3)半圆与弧:半圆是弧,但弧不一定是半圆.
(4)对于等弧的理解,从定义来看,要求的是能够完全重合的
弧为等弧,实质上,弧有长度和度数,规定半圆的度数为
180°,劣弧的度数小于180°,优弧的度数大于180°.若两条
弧为等弧,则必须满足长度及度数都相等,二者缺一不可.4.两个概念:
(1)圆心角:顶点在圆心的角;
(2)圆周角:顶点在圆上,并且两边都与圆相交的角.
圆心角的顶点在圆的内部,所以其边一定与圆相交;圆周角
必须满足两个条件,二者缺一不可.5.经过三角形三个顶点的圆叫做这个三角形的外接圆,这个三
角形叫做这个圆的内接三角形,三角形外接圆的圆心叫做这个
三角形的外心.
(1)一个三角形有且只有一个外接圆,但是一个圆有无数个内
接三角形.
(2)三角形的外心就是三角形三条边的垂直平分线的交点,到
三角形三顶点的距离相等,等于外接圆的半径.
(3)锐角三角形的外心在三角形的内部,直角三角形的外心是
斜边的中点,钝角三角形的外心在三角形的外部.6.与三角形各边都相切的圆叫做这个三角形的内切圆.三角形
的内切圆的圆心叫做这个三角形的内心,这个三角形叫做这个
圆的外切三角形.
(1)一个三角形有且只有一个内切圆,但是一个圆有无数个外
切三角形;
(2)三角形的内心是三角形三条角平分线的交点,它到三角形
三边的距离相等;
(3)与三角形内心有关的证明或计算,往往连结顶点与内心,
构造角平分线,应用角平分线的性质来证明或计算.7.圆的切线上某一点与切点之间的线段的长,叫做这点到圆的
切线长.
切线和切线长是两个不同的概念,切线是直线,不可度量,切
线长是切线上一条线段的长,可以度量.8.各边相等,各角也相等的多边形叫做正多边形.与之有关的
概念如图所示:
与正多边形有关的定义都是以正多边形的外接圆为基础的.在
理解定义时,要注意与多边形的相关元素之间的对应关系.二、圆的相关性质、判定及定理
1.垂径定理
(1)垂径定理及其推论
①垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
如图,⊙O中,若CD为直径,
CD⊥AB,垂足为M,则AM=BM,②平分弦(不是直径)的直径垂直于这条弦,并且平分弦所对的
弧;平分弧的直径垂直平分这条弧所对的弦.
如图,⊙O中,若AM=BM(AB不是直径),CD为直径,则AB⊥CD,
(2)理解垂径定理要注意以下问题:
①定理中的“垂径”可以是直径、半径或过圆心的直线,其本
质是“经过圆心”.②定理中的“弦”是直径时,结论仍然成立.
③垂径定理可以这样理解:一条直线,如果它具备两条:
a经过圆心;
b垂直于圆的一条弦.那么这条直线就具有另外三个性质:
a平分弦;
b平分弦所对的劣弧;
c平分弦所对的优弧.(3)垂径定理的其他推论
垂径定理成立的基础是圆的轴对称性,垂径定理及其推论可以
概括为:一条直线,如果它满足:①经过圆心;②垂直于圆的一
条弦;③平分弦;④平分弦所对的劣弧;⑤平分弦所对的优弧.
这五条中的任意两条,则必然具备其余三条,简称“知二推
三”.
注:在垂径定理的推论中,对被平分的弦不是直径的要求是不
可去掉的,在圆中任意的两条直径都是互相平分的,但是它们
不一定垂直.(4)垂径定理的应用
垂径定理是证明线段相等、角相等、垂直
关系、弧相等的重要依据,同时也为圆的
有关计算提供了方法和依据.
①应用垂径定理证明时,一般是过圆心作
弦的垂线,构造线段或弧相等.若有弦的中点,则连结圆心及弦
的中点,构造垂直关系.②与垂径定理有关的计算,一般是利用弦长的一半、弦心距、
半径所构成的直角三角形结合勾股定理及方程的思想求解.如图,常用的关系式为:r2= +d2,r=d+h等.若已知弦长a和弓形
的高h,则需要构建关于r的方程,利用方程的思想来解决.
③确定弧所在圆的圆心的方法,根据弦的垂直平分线经过圆
心,在弧上任意作两条弦,两弦的垂直平分线的交点就是弧所
在圆的圆心.
④应用垂径定理解决实际问题,关键是根据实际问题抽象出几
何模型,利用垂径定理来解决问题.2.弧、弦、圆心角、圆周角的关系
(1)弧、弦、圆心角之间的关系
在同圆或等圆中,有三组量:两个圆心角、两条弧、两条弦,
只要有一组量对应相等,它们所对应的其余各组量也都相等.
此定理成立的基础是圆的旋转不变性.在应用上述关系解决问题
时,可根据需要选取有关部分;“在同圆或等圆中”这一条件
不能漏掉,如在不同的圆中,相等的圆心角所对的弦及弧不一
定相等,但是相等的弧所对的圆心角一定相等,因为等弧只有
在同圆或等圆中才有可能存在.(2)圆周角定理及其推论
①在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该
弧所对的圆心角的一半;相等的圆周角所对的弧相等.
②半圆或直径所对的圆周角都相等,都等于90°(直角).
③90°的圆周角所对的弦是直径.
(3)圆内接四边形的性质:圆内接四边形的对角互补.3.切线的判定及性质
(1)切线的性质:圆的切线垂直于经过切点的半径.
①切线的性质可以作如下拓展:a切线和圆只有一个公共点;b
切线和圆心的距离等于圆的半径;c经过圆心且垂直于切线的直
线必过切点;d经过切点且垂直于切线的直线必过圆心.
②有圆的切线时,辅助线的作法一般是连结切点和圆心,构造
垂直关系来解题.(2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线
长相等,这一点和圆心的连线平分两条切线的夹角.
切线长定理能把许多圆的知识串联起来,并能找出一些规律性
的东西,便于应用,也有利于开阔思路.
如图,PA,PB分别切⊙O于A,B两点,直线OP交⊙O于D,E,
交弦AB于C,则:①由切线长定理得PA=PB,∠3=∠4.
②由等腰三角形三线合一得PC⊥AB,AC=BC.
③由垂径定理得:
④由切线性质定理得:OA⊥AP,OB⊥BP.
⑤连结AD,BD,由AD,BD分别平分∠PAB,∠PBA得:D为△ABP
的内心.
⑥∠1=∠2=∠3=∠4,∠5=∠6=∠7=∠8.(3)圆切线的判定方法
①定义:和圆只有一个公共点的直线是圆的切线.
②数量关系:和圆心距离等于半径的直线是圆的切线.
③判定定理:经过半径的外端且垂直于这条半径的直线是圆的
切线.
应用切线的判定定理证明直线与圆相切时,常用的辅助线的作
法为:(1)若已知直线与圆有公共点,则连结圆心和公共点证明
垂直,即“连半径,证垂直”;(2)若直线与圆的公共点没有确定,则过圆心作直线的垂线,证明圆心到直线的距离等于圆的
半径,即“作垂直,证等径”.
(4)直角三角形内切圆的半径与三边的关系
设直角三角形的两直角边为a,b,斜边为c,内切圆的半径为
r,则有 ,或 (由面积法得到).4.定理的应用
(1)在同圆或等圆中,证两弦相等时,常用的方法是找这两弦所
对的弧、圆心角、圆周角相等.同样,证明弧相等时,则考虑弧
所对的弦及有关的角之间存在的关系.
(2)利用圆周角定理解决问题时,常进行两种转化:一是利用同
弧所对的圆周角相等,进行角与角之间的转化;二是将圆周角
相等的问题转化为弦相等或弧相等或圆心角相等的问题.(3)把圆中的直径与90°的圆周角联系在一起,当题目中有直径
这一条件时,辅助线的作法一般是构造直径所对的圆周角是直
角,综合勾股定理等知识来解题.没有直径时常通过添加辅助线
作直径,创造条件,再利用圆周角的性质解题.
(4)若出现圆内接四边形,则利用其对角互补解决问题.
注:(1)在进行相关命题的判断时,易忽视“在同圆或等圆中”
这个条件而造成误判;
(2)与圆周角有关的问题常因图形不确定而产生多解的情况,此
时易忽视分情况进行讨论而导致丢解的错误.5.相切两圆的性质
如果两圆相切,那么切点一定在连心线上.
(1)要正确区别连心线和圆心距:连心线是通过不同心的两个圆
的圆心的一条直线,而圆心距是指两个圆心之间的线段的长度.
显然,两个圆的圆心的连线(线段)一定在连心线(直线)上.
(2)“相切两圆的连心线经过切点” ,也可理解为“相切两圆
的圆心、切点在同一条直线上” ,或“经过相切两圆的切点和
一个圆的圆心的直线必经过另一个圆的圆心” .(3)两圆相切时,连心线是常见的一条辅助线,使用连心线时要
注意:连心线是直线而不是线段;有时也用圆心距作辅助线.
注:由两圆相切的位置关系判断数量关系时,易忽视存在两种
情况而造成漏解.三、圆中的位置关系
1.点与圆的位置关系的判断方法
方法一:确定点和圆的位置关系,就是确定该点到圆心的距离
与半径的大小关系.先求出点到圆心的距离,并与圆的半径作比
较,如果P是圆所在平面内的一点,d表示点到圆心的距离,r表
示圆的半径,那么:
d<r ?P在圆内;d=r ?P在圆上;d>r ?P在圆外.方法二:利用圆内角、圆周角、圆外角三种角之间的大小来判
断,如果AB是⊙O的一条弦,点Q是⊙O上的一点,P点、Q点在直
线AB的同旁(如图),则有:
(1)∠APB>∠AQB?点P在圆内;
(2)∠APB=∠AQB?点P在圆上;
(3)∠APB<∠AQB?点P在圆外.2.直线与圆的位置关系
判断直线和圆的位置关系既可转化为直线和圆的交点的个数,
又可转化为点(圆心)到直线的距离与半径的大小关系.若⊙O的
半径为r,圆心O到直线l的距离为d,则具体情况如下表:3.圆和圆的位置关系
圆和圆的位置关系可以分为三大类:相离、相切、相交.相离包括外离与内含两种情况,相切包括外切与内切,在理解它们
时,要注意每个圆上的点相对于另一个圆的位置关系.
(1)圆和圆的位置关系,不但考虑了数(两圆公共点的个数),而
且考虑了形(两圆的位置关系),两圆的五种位置关系按公共点
的个数可分为0,1,2三大类.
(2)两圆外切和两圆内切,统一称为两圆相切,唯一的公共点称
为切点.
(3)具有内切或内含关系的两个圆的半径R与r不可能相等,即具
有内切或内含关系的两圆不可能为等圆,否则,这两个圆重合.四、圆中的相关计算
1.正多边形的有关计算
正n边形的半径和边心距把正n边形分成
2n个全等的直角三角形,由于这些直角
三角形的斜边都是正n边形的外接圆的半
径R,一条直角边是正n边形的边心距rn,
另一条直角边是正n边形的边长an的一半,
一个锐角是正n边形中心角αn的一半,即 另一个锐角为一个内角的一半,即 所以,根据上
面定理就可以把正n边形的有关计算归结为解直角三角形问题.
这样就把正n边形的计算问题转化为解直角三角形的问题.
计算公式:
(1)正n边形每个内角的度数:
(2)正n边形的中心角的度数:
(3)正n边形的每个外角的度数:(4)正n边形的对角线的条数:
注:(1)计算时易记错公式导致错误.
(2)易将正n边形的边心距和半径混淆.
2.弧长及扇形面积公式(半径为R的圆中)
(1)弧长:n°的圆心角所对的弧长
(2)扇形的面积:
①n°的圆心角所对的扇形面积
②弧长为l的扇形的面积弧是圆的一部分,扇形是圆面的一部分,所以在半径为R的圆
中,360°的圆心角所对的弧长就是圆的周长2πR,所以1°的
圆心角所对的弧长为 圆心角为1°的扇形的面积为
由此可以得到弧长和扇形的面积计算公式.
在公式中,n,180,360应理解为1°的倍数,计算时都不带单
位.扇形的第二个面积公式,与三角形的面积公式类似,为了便
于记忆,可以把扇形理解成一个曲边的等腰三角形.两个公式在
计算时要根据条件灵活选用.五、圆锥的侧面展开图与侧面积计算
圆锥的侧面展开图是一个扇形,这个扇形的半径是圆锥侧面的
母线、圆心是圆锥的顶点、弧长是圆锥底面圆的周长.
圆锥侧面积是扇形面积.
如果设扇形的半径为l,弧长为c,圆心角
为n°(如图),则它们之间有如下关系:同时,如果设圆锥底面半径为r,周长为c,侧面母线长为l,那么它的侧面积是:
圆锥的全面积为:πrl+πr2. 圆的对称性
【相关链接】
圆既是轴对称图形,又是中心对称图形.与之相关的定理有垂径
定理及其推论,圆心角、弧、弦之间的关系.它们是计算线段的
长度,证明线段相等、角相等、弧相等的重要依据.应用垂径定
理时,常作圆心到弦的垂线段,与半径、弦长的一半构成直角三
角形,结合勾股定理计算或证明.【例1】如图,DE是⊙O的直径,弦AB⊥DE,垂足
为C,若AB=6,CE=1,则OC=______,CD=______.【思路点拨】
【自主解答】如图连结OA,设⊙O的半径为R,
由垂径定理得AC= AB=3, OC=R-1,
根据勾股定理, AC2+OC2=OA2得
32+(R-1)2=R2,解得R=5, ∴OC=4,CD=9.
答案:4 9 圆周角定理及其推论
【相关链接】
圆周角定理提供了与圆有关的角的转化方法.圆周角与圆心角
的关系、同弧或等弧所对的圆周角相等是证明角相等的重要依
据,进而也可计算或证明有关线段的问题.在题目中,若有直径,
常作直径所对的圆周角,构造直角三角形,利用解直角三角形的
知识解决问题.【例2】如图,点A,B,C,D都在⊙O上,
OC⊥AB,∠ADC=30°,求∠BOC的度数. 【思路点拨】
【自主解答】∵点A,B,C,D都在⊙O上,OC⊥AB,
∵∠ADC=30°,
∴∠AOC=∠BOC=2∠ADC=60°,
∴∠BOC的度数为60°. 切线的性质与判定、切线长定理
【相关链接】
(1)在证明直线与圆的位置关系时,若有公共点,则连结公共点
与圆心,证半径与直线垂直;若直线与圆的公共点未知时,可作
出圆心到直线的垂线段,证明圆心到直线的距离和半径相等,从
而判定直线和圆相切;
(2)利用切线的性质时,常连结切点和圆心,则半径与切线垂
直;切线长定理与切线的性质定理的综合应用往往是证明线段
相等、角相等、弧相等及垂直关系的重要依据.【例3】如图,点A,E是半圆周上的三等分
点,直径BC=2,AD⊥BC,垂足为D,连结BE交AD于F,过A作
AG∥BE交BC于G.
(1)判断直线AG与⊙O的位置关系,并说明理由.
(2)求线段AF的长.【思路点拨】(1)
(2)
【自主解答】(1)AG与⊙O相切.
证明:连结OA,
∵点A,E是半圆周上的三等分点,
∴点A是 的中点,
∴OA⊥BE.
又∵AG∥BE,
∴OA⊥AG.
∴AG与⊙O相切.(2)∵点A,E是半圆周上的三等分点,
∴∠AOB=∠AOE=∠EOC=60°.
又OA=OB,
∴△ABO为正三角形.
又AD⊥OB,OB=1,
∴BD=OD= , AD= .
又∠EBC= =30°,
在Rt△FBD中, FD=BD·tan ∠EBC=BD ·tan 30°= 圆和圆的位置关系
【相关链接】
圆和圆的位置关系重点考查两圆相切和相交两种情况,其中相切
又分为外切和内切,在解题时常常因考虑不全而漏解.相交时常
添加的辅助线是两圆的公共弦,把两圆中的角或线段联系起来,
起到了桥梁的作用.【例4】如果两圆的半径分别为6和4,圆心距
为10,那么这两圆的位置关系是( )
(A)内含 (B)内切 (C)相交 (D)外切
【思路点拨】
【自主解答】选D.∵两圆的半径分别为4和6,圆心距为10,又
∵4+6=10,∴这两圆的位置关系是外切. 弧长和扇形、圆锥面积的相关计算
【相关链接】
(1)弧长和扇形面积的计算,关键是寻求所在圆的半径及弧所对
的圆心角;
(2)圆锥的侧面展开图是一个扇形,扇形的弧长为圆锥底面圆的
周长,半径为圆锥的母线;圆锥的高、母线和底面半径构成一个
直角三角形;
(3)计算不规则图形的面积时,常转化为规则图形
面积的和或差来解决.【例5】如图,Rt△ABC
中,∠ACB=90°,AC=BC= , 若把Rt△ABC
绕边AB所在直线旋转一周则所得的几何体
的表面积为( )
(A)4π (B)
(C)8π (D) 【思路点拨】
【自主解答】选D.由三角形绕斜边旋转后得到的,求表面积,实
际是两个圆锥的侧面积之和,一个圆锥的母线是原直角三角形的
一条直角边,半径是斜边的中线,等于2,圆锥的侧面是个扇形,其
弧长为圆锥底面圆的周长,即4π,其半径是圆锥的母线长,即AC
的长,然后再利用扇形的面积公式S= ×弧长×半径
则两个的和为【命题揭秘】
圆是数学的重点之一,也是中考的热点,纵观近几年中考,题型
包含选择题、填空题、解答题.在填空题、选择题里常常考的
是单独的一个知识点,如:圆周角、点与圆的位置关系、两圆
的位置关系、弧长的计算等,解答题是稍微综合点的,常常是几
个知识点综合起来考.常考的有:切线的性质与判定,垂径定理
或圆周角定理结合勾股定理或相似三角形来考.1.已知两圆的直径分别为2 cm和4 cm,圆心
距为3 cm,则这两个圆的位置关系是( )
(A)相交 (B)外切
(C)外离 (D)内含
【解析】选B.两圆半径分别为1 cm和2 cm,圆心距等于两圆半径
之和,所以这两个圆外切.2.如图所示,直线
CD与以线段AB为直径的圆相切于点D
并交BA的延长线于点C,且AB=2,AD=
1,P点在切线CD上移动.当∠APB的度
数最大时,∠ABP的度数为( )
(A)15° (B)30°
(C)60° (D)90°【解析】选B.当P点运动到点D时,此时∠APB=∠ADB为最大角.在直角三角形ABD中,AB=2,AD=1,所以∠ABP=30°.3.如图,AB是⊙O的
直径,点E为BC的中点,AB=4,∠BED
=120°,则图中阴影部分的面积之和
为( )
(A)1 (B)
(C) (D)【解析】选C.连结AE,
∵AB是直径,
∴∠AEB=90°,
又∵∠BED=120°,
∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD,
∴△AOD是等边三角形,∴∠A=60°,∵点E为BC的中点,∠AED=90°,
∴AB=AC,
∴△ABC是等边三角形.
△EDC是等边三角形,边长是2.
∴∠BOE=∠EOD=60°,
∴ 和弦BE围成的部分的面积= 和弦DE围成的部分的面积.
∴阴影部分的面积=
故选C.4.用圆心角为120°,半径为6 cm的扇形做成
一个无底的圆锥侧面,则此圆锥的底面半径为_____cm.
【解析】把n=120°,r=6代入 得l=4π;所以圆锥的底
面周长为4π,
则4π=2Rπ,所以R=2.
答案:25.母线长为3,底面圆的直径为2的圆锥的侧面
积为______.
【解析】
答案:3π6.如图,在直角坐标
系中,四边形OABC是直角梯形,BC∥OA,
⊙P分别与OA,OC,BC相切于点E,D,B,
与AB交于点F.已知A(2,0),B(1,2),
则tan∠FDE=______.【解析】连结BE.∵BC∥OA,∴BE为⊙P的直径.由A(2,0),
B(1,2),得BC=1,AO=2,BE=2,∴AE=2-1=1.在直角三角形ABE
中,tan∠FDE=tan∠ABE=
答案:7.如图,已知AD为⊙O的直径,B为AD延长线
上一点,BC与⊙O切于C点,∠A=30°.
求证:(1)BD=CD;
(2)△AOC≌△CDB.【证明】(1)∵AD为⊙O的直径,∴ ∠ACD=90°,
又∵∠A=30°,OA=OC=OD,
∴∠ACO=30°,∠ODC=∠OCD=60°,
又∵BC与⊙O切于C,
∴∠OCB=90°,∴∠BCD=30°,∴∠B=30°,
∴∠BCD=∠B,∴BD=CD.
(2)∵∠A=∠ACO=∠BCD=∠B=30°,
∴AC=BC,∴△AOC≌△BDC.8.如图,D为⊙O上一点,点C在直径BA的延长
线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=6,
tan∠CDA= ,求BE的长.【解析】(1)如图,连结OD,
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又AB是⊙O的直径,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°即∠CDO=90°,
∴CD是⊙O的切线.(2)由tan∠CDA=tan∠ABD=
∵∠C=∠C,∠CDA=∠CBD,
∴△CAD∽△CDB,
∵BC=6,∴CD=4。
∵CE,BE是⊙O的切线,
∴BE=DE,BE⊥BC,
∴BE2+BC2=EC2即(4+BE)2=62+BE2,解得BE=【拓展思维】
圆中常见辅助线口诀
半径与弦长计算,弦心距来中间站.
圆上若有一切线,切点圆心半径连.
切线长度的计算,勾股定理最方便.
要想证明是切线,半径垂线仔细辨.
是直径,成半圆,想成直角径连弦.
弧有中点圆心连,垂径定理要记全.
圆周角边两条弦,直径和弦端点连.弦切角边切线弦,同弧对角等找完.
要想作个外接圆,各边作出中垂线.
还要作个内接圆,内角平分线梦圆.
如果遇到相交圆,不要忘作公共弦.
内外相切的两圆,经过切点公切线.
若是添上连心线,切点肯定在上面.
要作等角添个圆,证明题目少困难.9.如图,△ABC内
接于⊙O,直径BD交AC于E,过O作FG
⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OF·DE=OE·2OH;
(2)若⊙O的半径为12,且OE∶OF∶OD
=2∶3∶6,求阴影部分的面积.
(结果保留根号)【解析】(1)∵BD是直径,∴∠DAB=90°.
∵FG⊥AB,∴DA∥FO.
∴∠EOF=∠EDA,∠EFO=∠EAD.
∴△FOE∽△ADE.
即OF·DE=OE·AD.
∵O是BD的中点,DA∥OH,
∴AD=2OH.
∴OF·DE=OE·2OH.(2)∵⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,
∴OE=4,ED=8,OF=6.
代入(1)结论,得AD=12. ∴OH=6.
在Rt△ABC中,OB=2OH,∴∠BOH=60°.
∴BH=BO·sin60°=
∴S阴影=S扇形GOB-S△OHB
