2020春华师版九下数学 圆27.1.2圆的对称性课件(37张PPT)
文档属性
| 名称 | 2020春华师版九下数学 圆27.1.2圆的对称性课件(37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 901.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 23:21:04 | ||
图片预览











文档简介
课件37张PPT。2.圆的对称性 1.圆的对称性
(1)圆是_________图形,无论绕_____旋转多少度,仍与自身重合,
对称中心是_____,因而圆也是中心对称图形.
(2)圆是___对称图形,它的任意一条_____所在的直线都是它的对
称轴.旋转对称圆心圆心轴直径2.圆心角、弧、弦之间的关系
(1)探究:如图,请完成下列问题:
①∵ ∴∠AOB=______,AB=___.
②∵AB=CD,∴∠AOB=______, =___.
③∵∠AOB=∠COD,∴AB=___, =___.∠CODCD∠CODCD(2)圆心角、弧、弦之间的关系:
在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量
_____,那么它们所对应的其余各组量都分别_____. 相等相等3.垂径定理及推论
(1)垂径定理:垂直于弦的直径_____这条弦,并且_____弦所对的
两条弧.
(2)推论:①平分弦(不是直径)的直径_____于这条弦,并且_____
弦所对的弧.
②平分弧的直径_________这条弧所对的弦.
【点拨】圆心角、弧、弦三者之间的关系可由旋转对称性推
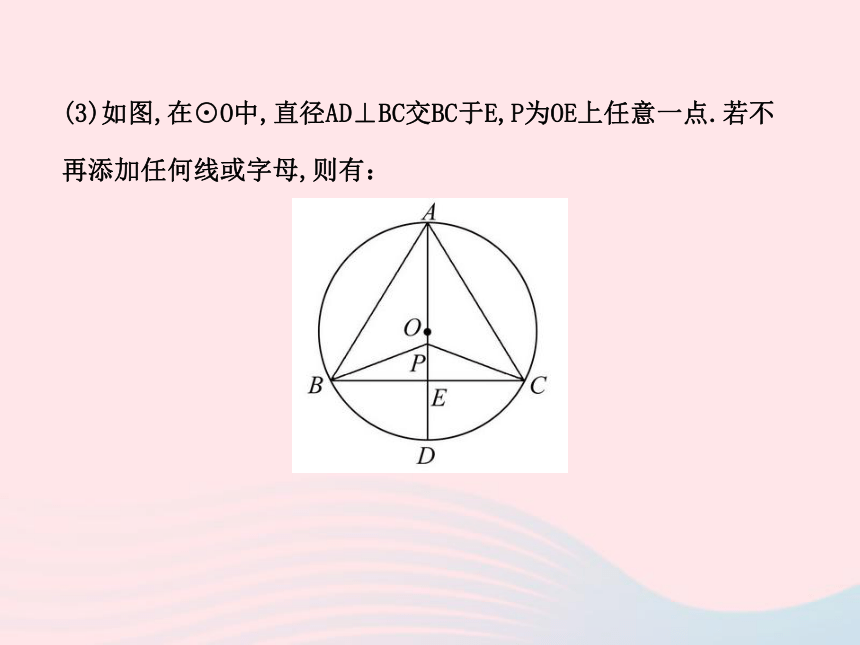
导;垂径定理及推论可由圆的轴对称性推导.平分平分垂直平分垂直平分(3)如图,在⊙O中,直径AD⊥BC交BC于E,P为OE上任意一点.若不
再添加任何线或字母,则有:①相等的线段有:____________________;
②全等的三角形有:
_______________________________________;
③相等的角有:
________________________________________________,
________________________;
④相等的劣弧有:_______________.△ABP≌△ACP,△BPE≌△CPE,△ABE≌△ACE∠ABE=∠ACE,∠AEB=∠AEC,∠ABP=∠ACP,∠APB=∠APC∠BPE=∠CPE,∠BAE=∠CAEBE=CE,AB=AC,BP=CP【预习思考】圆心角、弧、弦间的关系成立的前提是什么?
提示:圆心角、弧、弦间的关系成立的前提是“在同一个圆中”,对于等圆,关系仍然成立. 圆心角、弧、弦之间的关系
【例1】如图所示,在⊙O中,AB为直径,AC=AD.求证:【解题探究】1.在⊙O中,要证 则证得两弧所对的圆心角
相等即可,即需要证明∠COB=∠BOD;
2.在条件中有弦AC与弦AD相等,根据圆心角、弧、弦三者之间的
关系可得∠AOC=∠AOD;
3.由图可以得出:∠COB+∠AOC=180°,∠AOD+∠BOD=180°;结
合2可得出∠COB=∠BOD,从而证明【互动探究】在运用圆心角和它所对的弧相等时,应注意什么?
提示:圆心角和它所对的弧相等,这里的相等指的是“角与弧的
度数相等”,而不是“角与弧相等” 【规律总结】
运用圆心角定理时应注意的两个问题
1.圆心角、弧、弦之间的关系的结论必须在同圆或等圆中才能
成立;
2.一条弦所对的弧有两条,应用时应注意区分.【跟踪训练】
1.下列结论正确的是( )
(A)长度相等的两条弧是等弧
(B)半圆是弧
(C)相等的圆心角所对的弧相等
(D)弧是半圆【解析】选B.A.根据圆内相关定义,能够完全重合的弧是等
弧,故本选项错误;
B.弧分为优弧、劣弧、半圆,故本选项正确;
C.根据在同圆或等圆中,相等的圆心角所对的弧相等,
故本选项错误;
D.弧分为优弧、劣弧、半圆,故本选项错误.2.如图,已知:AB是⊙O的直径,C,D是 上的三等分点,
∠AOE=60°,则∠COE是( )
(A)40° (B)60° (C)80° (D)120° 【解析】选C.∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,
∴ 的度数是120°.
∵C,D是 上的三等分点,
∴ 与 的度数都是40°,
∴∠COE=80°.3.如图,在⊙O中, ∠A=40°,
则∠B=______度.
【解析】∵
∴AB=AC.
∵∠A=40°,
∴∠B=∠C=(180°-∠A)÷2=70°.
答案:70 垂径定理的应用
【例2】如图,⊙O的
半径为17 cm,弦AB∥CD,AB=30 cm,CD=
16 cm,圆心O位于AB,CD的上方,求AB和CD
间的距离.
易错提醒:不能正确解答此类问题的原因有:①不会作辅助线;
②想不到利用勾股定理. 【规范解答】分别作弦AB,CD的弦心距,设垂足分别为E,F,
∵AB=30 cm,
CD=16 cm,
∴AE=
CF= ………………………………2分
在Rt△AOE中,
OE=在Rt△OCF中,OF=
=15(cm),……………………………………………………6分
∴EF=OF-OE=15-8=7(cm). …………………………………8分【规律总结】
在运用垂径定理时辅助线的作法及两点注意
1.辅助线作法:有关圆内弦的长度计算,一般情况下,经常过
圆心作垂直于弦的半径,构建直角三角形.
2.两点注意:
(1)这里的垂径可以是直径、半径,也可以是过圆心的直线或线
段;
(2)条件中的“弦”可以是直径,结论中的“平分弧”既意味着
平分弦所对的劣弧,又意味着平分弦所对的优弧.【跟踪训练】
4.如图,⊙O的直径CD=5 cm,AB是⊙O的弦,
AB⊥CD,垂足为M,OM∶OD=3∶5,则AB 的长是( )
(A)2 cm (B)3 cm (C)4 cm (D)【解析】选C.连结OA,
⊙O的直径CD=5?OC=OD=2.5
OM∶OD=3∶5
在Rt△AOM中,
AB⊥CD?AB=2AM=4.5.已知⊙O的直径AB=40,弦CD⊥AB于点E,且
CD=32,则AE的长为( )
(A)12 (B)8
(C)12或28 (D)8或32【解析】选D.依据题意,画出如图图形,连结OC,由CD⊥AB,可得
∠OEC=90°,在Rt△OEC中,OC= 所以
OE= 所以当点E在线段AO上时,AE=
AO-OE=20-12=8;当点E在线段OB上时,AE=AO+OE=20+12=32.6.如图,AB是⊙O的弦,OC⊥AB于C,若AB=
OC=1,则半径OB的长为________.
【解析】∵OC⊥AB,根据垂径定理,得BC=
在Rt△OCB中,根据勾股定理,得
答案:27.如图,已知AB是⊙O的弦,半径OA=20 cm,
∠AOB=120°,求△AOB的面积.
【解析】作OC⊥AB于点C,则有AC=CB,∠AOC=
在Rt△AOC中,OA=20 cm,所以AC= cm,OC=10 cm.
所以△AOB的面积 1.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,
则∠BCD=( )
(A)105° (B)120° (C)135° (D)150°【解析】选B.由题意知,弦BC,CD,DA三等分半圆,
∴弦BC,CD和DA对的圆心角均为60°,
连结OD,OC,则△DOC,△BOC为等边三角形,
∴∠BCO=∠OCD=60°.
∴∠BCD=120°. 2.如图,AB为⊙O的直径,弦CD⊥AB于E,已
知CD=12,BE=2,则⊙O的直径为( )
(A)8 (B)10 (C)16 (D)20
【解析】选D.连结OC,设OC=R,则OE=R-2,由垂径定理得CE=6,
由勾股定理得62+(R-2)2=R2,解得R=10,所以⊙O的直径为20.3.如图,D,E分别是⊙O的半径OA,OB上的点,CD⊥OA,CE⊥OB,
CD=CE,则 弧长的大小关系是__________.【解析】∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°,CD=CE,CO=CO,
∴△COD≌△COE.
∴∠AOC=∠BOC.
∴
答案:相等4.当宽为3 cm的刻度尺的一边与圆相切
时,另一边与圆的两个交点处的读数如图所示(单位:cm),
那么该圆的半径为_______ cm.【解析】过圆心作弦的垂线,设该圆的半径为R,
则弦心距为R-3,
由勾股定理得:
得R= cm,即该圆半径为 cm.
答案:5.如图,点C,D分别在扇形AOB的半径OA,OB
的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M,N.
(1)求线段OD的长;
(2)若tan∠C= 求弦MN的长.【解析】(1)∵CD∥AB,∴∠OAB=∠C,∠OBA=∠D.
∵OA=OB,∴∠OAB=∠OBA,
∴∠C=∠D,∴OC=OD.
∵OA=3,AC=2,
∴OC=5.
∴OD=5.(2)过点O作OE⊥CD,E为垂足,连结OM.
在Rt△OCE中,OC=5,tan∠C=
设OE=x,则CE=2x.
由勾股定理得x2+(2x)2=52,
解得x1= ,x2= (舍去).∴OE= .
在Rt△OME中,OM=OA=3,
ME=
∴MN=2ME=4.
(1)圆是_________图形,无论绕_____旋转多少度,仍与自身重合,
对称中心是_____,因而圆也是中心对称图形.
(2)圆是___对称图形,它的任意一条_____所在的直线都是它的对
称轴.旋转对称圆心圆心轴直径2.圆心角、弧、弦之间的关系
(1)探究:如图,请完成下列问题:
①∵ ∴∠AOB=______,AB=___.
②∵AB=CD,∴∠AOB=______, =___.
③∵∠AOB=∠COD,∴AB=___, =___.∠CODCD∠CODCD(2)圆心角、弧、弦之间的关系:
在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量
_____,那么它们所对应的其余各组量都分别_____. 相等相等3.垂径定理及推论
(1)垂径定理:垂直于弦的直径_____这条弦,并且_____弦所对的
两条弧.
(2)推论:①平分弦(不是直径)的直径_____于这条弦,并且_____
弦所对的弧.
②平分弧的直径_________这条弧所对的弦.
【点拨】圆心角、弧、弦三者之间的关系可由旋转对称性推
导;垂径定理及推论可由圆的轴对称性推导.平分平分垂直平分垂直平分(3)如图,在⊙O中,直径AD⊥BC交BC于E,P为OE上任意一点.若不
再添加任何线或字母,则有:①相等的线段有:____________________;
②全等的三角形有:
_______________________________________;
③相等的角有:
________________________________________________,
________________________;
④相等的劣弧有:_______________.△ABP≌△ACP,△BPE≌△CPE,△ABE≌△ACE∠ABE=∠ACE,∠AEB=∠AEC,∠ABP=∠ACP,∠APB=∠APC∠BPE=∠CPE,∠BAE=∠CAEBE=CE,AB=AC,BP=CP【预习思考】圆心角、弧、弦间的关系成立的前提是什么?
提示:圆心角、弧、弦间的关系成立的前提是“在同一个圆中”,对于等圆,关系仍然成立. 圆心角、弧、弦之间的关系
【例1】如图所示,在⊙O中,AB为直径,AC=AD.求证:【解题探究】1.在⊙O中,要证 则证得两弧所对的圆心角
相等即可,即需要证明∠COB=∠BOD;
2.在条件中有弦AC与弦AD相等,根据圆心角、弧、弦三者之间的
关系可得∠AOC=∠AOD;
3.由图可以得出:∠COB+∠AOC=180°,∠AOD+∠BOD=180°;结
合2可得出∠COB=∠BOD,从而证明【互动探究】在运用圆心角和它所对的弧相等时,应注意什么?
提示:圆心角和它所对的弧相等,这里的相等指的是“角与弧的
度数相等”,而不是“角与弧相等” 【规律总结】
运用圆心角定理时应注意的两个问题
1.圆心角、弧、弦之间的关系的结论必须在同圆或等圆中才能
成立;
2.一条弦所对的弧有两条,应用时应注意区分.【跟踪训练】
1.下列结论正确的是( )
(A)长度相等的两条弧是等弧
(B)半圆是弧
(C)相等的圆心角所对的弧相等
(D)弧是半圆【解析】选B.A.根据圆内相关定义,能够完全重合的弧是等
弧,故本选项错误;
B.弧分为优弧、劣弧、半圆,故本选项正确;
C.根据在同圆或等圆中,相等的圆心角所对的弧相等,
故本选项错误;
D.弧分为优弧、劣弧、半圆,故本选项错误.2.如图,已知:AB是⊙O的直径,C,D是 上的三等分点,
∠AOE=60°,则∠COE是( )
(A)40° (B)60° (C)80° (D)120° 【解析】选C.∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,
∴ 的度数是120°.
∵C,D是 上的三等分点,
∴ 与 的度数都是40°,
∴∠COE=80°.3.如图,在⊙O中, ∠A=40°,
则∠B=______度.
【解析】∵
∴AB=AC.
∵∠A=40°,
∴∠B=∠C=(180°-∠A)÷2=70°.
答案:70 垂径定理的应用
【例2】如图,⊙O的
半径为17 cm,弦AB∥CD,AB=30 cm,CD=
16 cm,圆心O位于AB,CD的上方,求AB和CD
间的距离.
易错提醒:不能正确解答此类问题的原因有:①不会作辅助线;
②想不到利用勾股定理. 【规范解答】分别作弦AB,CD的弦心距,设垂足分别为E,F,
∵AB=30 cm,
CD=16 cm,
∴AE=
CF= ………………………………2分
在Rt△AOE中,
OE=在Rt△OCF中,OF=
=15(cm),……………………………………………………6分
∴EF=OF-OE=15-8=7(cm). …………………………………8分【规律总结】
在运用垂径定理时辅助线的作法及两点注意
1.辅助线作法:有关圆内弦的长度计算,一般情况下,经常过
圆心作垂直于弦的半径,构建直角三角形.
2.两点注意:
(1)这里的垂径可以是直径、半径,也可以是过圆心的直线或线
段;
(2)条件中的“弦”可以是直径,结论中的“平分弧”既意味着
平分弦所对的劣弧,又意味着平分弦所对的优弧.【跟踪训练】
4.如图,⊙O的直径CD=5 cm,AB是⊙O的弦,
AB⊥CD,垂足为M,OM∶OD=3∶5,则AB 的长是( )
(A)2 cm (B)3 cm (C)4 cm (D)【解析】选C.连结OA,
⊙O的直径CD=5?OC=OD=2.5
OM∶OD=3∶5
在Rt△AOM中,
AB⊥CD?AB=2AM=4.5.已知⊙O的直径AB=40,弦CD⊥AB于点E,且
CD=32,则AE的长为( )
(A)12 (B)8
(C)12或28 (D)8或32【解析】选D.依据题意,画出如图图形,连结OC,由CD⊥AB,可得
∠OEC=90°,在Rt△OEC中,OC= 所以
OE= 所以当点E在线段AO上时,AE=
AO-OE=20-12=8;当点E在线段OB上时,AE=AO+OE=20+12=32.6.如图,AB是⊙O的弦,OC⊥AB于C,若AB=
OC=1,则半径OB的长为________.
【解析】∵OC⊥AB,根据垂径定理,得BC=
在Rt△OCB中,根据勾股定理,得
答案:27.如图,已知AB是⊙O的弦,半径OA=20 cm,
∠AOB=120°,求△AOB的面积.
【解析】作OC⊥AB于点C,则有AC=CB,∠AOC=
在Rt△AOC中,OA=20 cm,所以AC= cm,OC=10 cm.
所以△AOB的面积 1.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,
则∠BCD=( )
(A)105° (B)120° (C)135° (D)150°【解析】选B.由题意知,弦BC,CD,DA三等分半圆,
∴弦BC,CD和DA对的圆心角均为60°,
连结OD,OC,则△DOC,△BOC为等边三角形,
∴∠BCO=∠OCD=60°.
∴∠BCD=120°. 2.如图,AB为⊙O的直径,弦CD⊥AB于E,已
知CD=12,BE=2,则⊙O的直径为( )
(A)8 (B)10 (C)16 (D)20
【解析】选D.连结OC,设OC=R,则OE=R-2,由垂径定理得CE=6,
由勾股定理得62+(R-2)2=R2,解得R=10,所以⊙O的直径为20.3.如图,D,E分别是⊙O的半径OA,OB上的点,CD⊥OA,CE⊥OB,
CD=CE,则 弧长的大小关系是__________.【解析】∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°,CD=CE,CO=CO,
∴△COD≌△COE.
∴∠AOC=∠BOC.
∴
答案:相等4.当宽为3 cm的刻度尺的一边与圆相切
时,另一边与圆的两个交点处的读数如图所示(单位:cm),
那么该圆的半径为_______ cm.【解析】过圆心作弦的垂线,设该圆的半径为R,
则弦心距为R-3,
由勾股定理得:
得R= cm,即该圆半径为 cm.
答案:5.如图,点C,D分别在扇形AOB的半径OA,OB
的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M,N.
(1)求线段OD的长;
(2)若tan∠C= 求弦MN的长.【解析】(1)∵CD∥AB,∴∠OAB=∠C,∠OBA=∠D.
∵OA=OB,∴∠OAB=∠OBA,
∴∠C=∠D,∴OC=OD.
∵OA=3,AC=2,
∴OC=5.
∴OD=5.(2)过点O作OE⊥CD,E为垂足,连结OM.
在Rt△OCE中,OC=5,tan∠C=
设OE=x,则CE=2x.
由勾股定理得x2+(2x)2=52,
解得x1= ,x2= (舍去).∴OE= .
在Rt△OME中,OM=OA=3,
ME=
∴MN=2ME=4.
