人教版六年级数学《数的认识》总复习课件(43张PPT)
文档属性
| 名称 | 人教版六年级数学《数的认识》总复习课件(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览











文档简介
(共56张PPT)
2011~2012学年度六年级数学总复习
★数与代数
数的认识
分数和百分数
整数和小数
数的整除
1.自然数,0和整数
数物体的时候,用来表示物体个数的0,1,2,3…叫做自然数.
一个物体也没有用0表示.
0也是自然数.
0和自然数都是整数.0是最小的自然数,没有最大的自然数。
自然数的单位是1.
但不能说整数只包括0和自然数
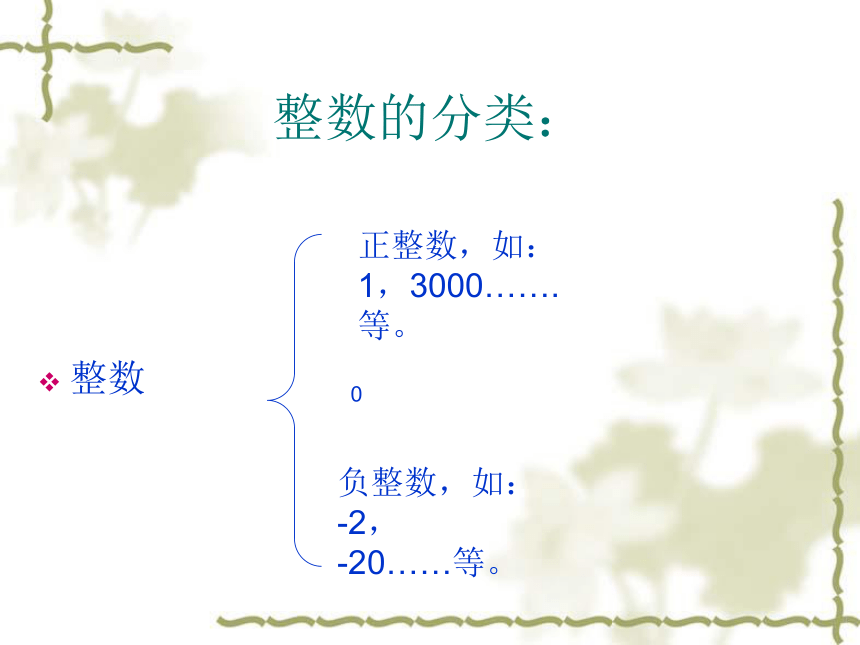
整数的分类:
整数
正整数,如:1,3000…….等。
0
负整数,如:-2, -20……等。
正数和负数的意义
正数:像16,2000,8.3,…这样的数叫正数。
负数:像-0.3,-45,-7800 …这样的数叫负数。
0既不是正数也不是负数。
2.十进制计数法
计数单位: 一(个)、十、百、千、万…… 及十分之一、百分之一、千分之一……都叫做计数单位.其中“一”是计数的基本单位.10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是十.这种计数方法叫做十进制计数法.
数位:各个计数单位所占的位置,叫数位。数位是按照一定顺序排列的。
数的分级:按照我国的计数习惯,整数部分从个位起,每四个数位是一级,从低级到高级一次为个级,万级,亿级,分别表示多少个一,多少个万,多少个亿…
3.整数的读法和写法
读数时,从高位起,一级一级地往下读,属于亿级和万级的要读出级名.
读数时,每级末尾的“0”都不读,其他数位有一个0或连续几个0都只读一个0.
8000406000读作:
写数时,从高位起,一级一级地往下写,哪一位上一个单位也没有,就在哪个数位上写0
六亿八千四百五十二万八千五百六十三.
684528563读作:
八十亿零四十万六千.
4.四舍五入法
求一个数的近似数,要看尾数的最高位上的数是几,如果比5小,就把尾数都舍去;如果尾数最高位上的数是5或大于5,就把尾数舍去后,要向它的前一位进1.
5.整数大小的比较
比较两个多位数的大小,首先看它们位数的多少,位数较多的数较大;
如果两个数的位数相同,那么首先看最高位,最高位上的数较大的,这个数就大;
如果最高位相同,则左边第二位上的数较大的,这个数就大……
6.小数
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示.
小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一……
小数部分的最大计数单位是十分之一,没有最小的计数单位.
小数部分有几个数位,就叫做几位小数.
7.小数的读法和写法
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字.
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字.
如 45.469 读作:
四十五点四六九
8.小数的性质
小数的末尾添上0或者去掉0,小数的大小不变.
运用小数的性质,可以在小数末尾添上0.
3.5=3.50
也可以把小数化简.
3.500=3.5
9.小数点数位移动引起小数大小的变化
小数点向右移动一位、两位、三位……原来的数就扩大10倍、100倍、1000倍……
小数点向左移动一位、两位、三位……原来的数就缩小10倍、100倍、1000倍……
如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足.
10.循环小数
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数.
如 0.5555…… 7.23838……
依次不断重复出现的数字叫做循环节.
循环小数的简便记法
0.5555…… 记作:0.5
7.23838……记作:7.238
.
..
10.循环小数
循环节从小数部分第一位开始的叫纯循环小数.如 0.5
循环节不是从小数部分第一位开始的叫混循环小数.如7.238
.
..
11.小数的分类
(1).按小数位数是有限还是无限分
(2).按小数的整数部分是否为0分
12.数的改写
一个较大的多位数,为了读写方便,常常把它改写成用
“万”或“亿”作单位的数.有时还可以根据需要,省略这个数某
一位后面的尾数,写成近似数.
把76450000改写成用“万”作单位的数是( )
把235800改写成用“万”作单位的数是( )
235800省略万位后面的尾数约为( )
把34562800000改写成用“亿”作单位的数后,保留两位
小数是( )
4.62975保留两位小数是:( )
4.62975保留三位小数是:( )
7645万
23.58万
24万
345.63亿
4.63
4.630
1.分数的意义和分数单位
单位“1”----
一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”
分 数----
分数各部分的名称:
分数单位----
把单位“1”平均分成若干份,表示其中的一份的数.
(表示平均分的份数)
(表示所取的份数)
把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数.
2.分数与除法
分数与除法的关系:
被除数÷除数=
(除数≠0)
把单位“1”平均分成9份,取其中的5份.
把5米平均分成9份,每份是( ),
每份是( )米.
3.分数大小的比较
★分母相同的两个分数,分子大的分数比较大.
★分子相同的两个分数,分母小的分数比较大.
<
>
<
>
★通分:先求出原来几个分母的最小公倍数,然后把各个
分数分别化成用这个最小公倍数作分母的分数.
<
4.分数的分类
真分数----
假分数----
分子比分母小的分数.
分子比分母大或者分子和分母
相等的分数.
真分数<1
假分数≥1
5.分数的基本性质
分数的分子和分母同时乘以或者除以相同的数
(零除外),分数的大小不变.
一个分数的分母不变,分子乘以3,则这个分数( )
如果分子不变,分母除以5,则这个分数( )
扩大3倍
扩大5倍
6.最简分数
*计算的结果,能约分的要约成最简分数;
假分数的,一般要化成带分数或整数.
*判断一个最简分数能不能化成有限小数:
分母中除了2和5以外,不含有其他的质因数,就能化成有限小数.
√
√
√
√
√
7.约分
约分------把一个分数化成和它相等,但分子和分母
都比较小的分数.
约分的方法:
1.用分子分母的公因数(1除外)逐次去除分子和
分母,直到得到最简分数为止.
2.用分子和分母的最大公因数去除分子和分母.
8.百分数的意义
表示一个数是另一个数的百分之几的数叫百分数.
百分数又叫百分率或百分比.
9.分数、小数、百分数的互化
小数
分数
百分数
0.25=( )
小数点向右移动两位,添上%
0.35%=( )
去掉%,小数点向左移动两位
先化成小数,再化成百分数
先写成分数,再约分
先用分数表示,再约分
分子除以分母
=
40%=
2
5
1
6
≈0.167=16.7%
1
4
=0.25=25%
1.2=
25%
0.0035
数的整除
1. 整除与除尽
2. 约数和倍数
3. 能被2.3.5整除的数的特征
4. 偶数和奇数
5. 质数和合数
6. 质因数和分解质因数
7. 最大公因数和最小公倍数
1. 整除与除尽
整除:
整数a除以整数b(b≠0),除得的商是整数而没有余数,
我们就说数a能被数b整除,或数b能整除a.
除尽:
数a除以数b(b≠0),除得的商是整数或是有限小数,
这就叫做除尽.
整除是除尽的一种特殊情况,整除也可以说是除尽,
但除尽不一定是整除.
区别:
2. 因数和倍数
如果a×b=c(a.b.c都不为0),那么a、b就叫做c的因数.c叫做a、b的倍数。(研究因数和倍数不考虑0)。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身.
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数.
因数和倍数是相互依存的
一个数既是本身的最大因数,也是本身最小的倍数。
3. 2.3.5倍数的特征
2的倍数的特征:
5的倍数的特征:
3的倍数的特征:
个位上是0,2,4,6,8,
个位上是0或5
各个数位上的数字的和是3的倍数
既是2的倍数,又是5的倍数的数的特征:
既是2的倍数,又是3,5的倍数的数的特征:
个位是0,而且各个位上的数字的和能被3整除.
注意:有一些数是7,9,11,13的倍数,但是不容易看出来,
这是大家在约分中容易忽略的.
个位是0
4. 偶数和奇数
一个自然数,不是奇数就是偶数
偶数:
是2的倍数的数叫做偶数
奇数:
不是2的倍数的数叫做奇数
偶数±偶数=( ) 奇数±奇数=( ) 偶数±奇数=( )
偶数×偶数=( ) 奇数×奇数=( ) 偶数×奇数=( )
偶数
偶数
偶数
偶数
奇数
奇数
最小的偶数是:
最小的奇数是:
0
1
5. 质数和合数
质数:
(素数)
只有1和它本身两个因数的数
合数:
除了1和它本身还有别的因数的数
1: 既不是质数也不是合数
最小的质数是:
最小的合数是:
2
4
要求:熟记100以内的质数表。
2是唯一的偶质数
6. 质因数和分解质因数
质因数:
分解质因数:
每一个合数都可以写成几个质数相乘的形式,
这几个质数叫做这个合数的质因数.
把一个合数用几个质因数相乘的形式表示出来.
叫做分解质因数.
分解质因数的方法:短除法
把30分解质因数正确的做法是( )
A.30=1×2 ×3 ×5
B.2 ×3 ×5=30
C.30=2×3×5
C
把30分解质因数
公因数,最大公因数:
几个数公有的因数,叫做这几个数的公因数;
其中最大的一个叫做这几个数的最大公因数.
例:( )是8和12的公因数,( )是8和12的最大公因数.
1,2,4
4
公倍数,最小公倍数:
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数.
例:( …)都是4和6的公倍数,( )是4和6的最小公倍数.
12,24,36
12
互质数:
公因数只有1的两个数叫做互质数.
⑴、两个数都是质数,这两个数一定互质.
⑵、相邻的两个数互质.
⑶、1和任何数都互质.
互质数的几种特殊情况
7. 最大公因数和最小公倍数
求最大公因数和最小公倍数
4和28 最大公因数是( ); 最小公倍数是( )
⑴.如果较小数是较大数的因数,那么较小数就是
这两个数的最大公因数;较大数就是这两个数的
最小公倍数.
4和15 最大公因数是( ); 最小公倍数是( )
⑵.如果两个数互质,它们的最大公因数就是1;
最小公倍数就是它们的积.
4
28
1
60
⑶.短除法
求24和36的最大公因数和最小公倍数
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
质数
数的运算1
——四则运算各部分之间的关系
各部分间的关系
加法 和=加数+加数 一个加数=和-另一个加数
减法 被减数-减数=差 减数=被减数-差 被减数=差+减数
乘法 因数×因数=积 一个因数=积÷另一个因数
除法 被除数÷除数=商 被除数=商×除数 除数=被除数÷商
四则运算定律和运算性质
加法交换律 a +b =b+a
加法结合律 a+b+c=a+(b+c)
乘法交换律 a×b=b×a
乘法结合律 a×b×c= a×(b×c )
乘法分配律 (a+b) ×c= a×c+ b×c
运算性质
减法的运算性质: a-(b+c)=a-b-c
a-b-c= a-(b+c)
除法的运算性质: a÷(b×c)= a÷b÷c
a÷b÷c= a÷(b×c)
0与1在四则运算中的特殊性
a+0=a a-0=a
a-a=0 a×0=0
a×0=0 a×1=a
a÷1=a 0÷a=0
1÷a= a÷a=1
四则运算的顺序
1、 四则运算分为两级:加法和减法为第一级运算,乘法和除法为第二级运算
2、 四则混合运算的顺序:
(1)在没有括号的算式里,如果只有同级计算,从左往右按顺序计算;如果有两级计算,要先算第二级计算,再算第一级计算。
(2)有括号的先算小括号里面的,再算中括号里面的,最后算括号外面的。
数的运算2:解决问题
常用的两种分析方法:
1、综合法:从已知数量和已知数量关系入手,利用已知信息看能解决什么问题,直到求出未知数量的解题方法。
2、分析法:从所求的问题出发,逐步找出解答问题所需的条件,依次推导,直到问题得到解决。
2011~2012学年度六年级数学总复习
★数与代数
数的认识
分数和百分数
整数和小数
数的整除
1.自然数,0和整数
数物体的时候,用来表示物体个数的0,1,2,3…叫做自然数.
一个物体也没有用0表示.
0也是自然数.
0和自然数都是整数.0是最小的自然数,没有最大的自然数。
自然数的单位是1.
但不能说整数只包括0和自然数
整数的分类:
整数
正整数,如:1,3000…….等。
0
负整数,如:-2, -20……等。
正数和负数的意义
正数:像16,2000,8.3,…这样的数叫正数。
负数:像-0.3,-45,-7800 …这样的数叫负数。
0既不是正数也不是负数。
2.十进制计数法
计数单位: 一(个)、十、百、千、万…… 及十分之一、百分之一、千分之一……都叫做计数单位.其中“一”是计数的基本单位.10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是十.这种计数方法叫做十进制计数法.
数位:各个计数单位所占的位置,叫数位。数位是按照一定顺序排列的。
数的分级:按照我国的计数习惯,整数部分从个位起,每四个数位是一级,从低级到高级一次为个级,万级,亿级,分别表示多少个一,多少个万,多少个亿…
3.整数的读法和写法
读数时,从高位起,一级一级地往下读,属于亿级和万级的要读出级名.
读数时,每级末尾的“0”都不读,其他数位有一个0或连续几个0都只读一个0.
8000406000读作:
写数时,从高位起,一级一级地往下写,哪一位上一个单位也没有,就在哪个数位上写0
六亿八千四百五十二万八千五百六十三.
684528563读作:
八十亿零四十万六千.
4.四舍五入法
求一个数的近似数,要看尾数的最高位上的数是几,如果比5小,就把尾数都舍去;如果尾数最高位上的数是5或大于5,就把尾数舍去后,要向它的前一位进1.
5.整数大小的比较
比较两个多位数的大小,首先看它们位数的多少,位数较多的数较大;
如果两个数的位数相同,那么首先看最高位,最高位上的数较大的,这个数就大;
如果最高位相同,则左边第二位上的数较大的,这个数就大……
6.小数
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示.
小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一……
小数部分的最大计数单位是十分之一,没有最小的计数单位.
小数部分有几个数位,就叫做几位小数.
7.小数的读法和写法
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字.
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字.
如 45.469 读作:
四十五点四六九
8.小数的性质
小数的末尾添上0或者去掉0,小数的大小不变.
运用小数的性质,可以在小数末尾添上0.
3.5=3.50
也可以把小数化简.
3.500=3.5
9.小数点数位移动引起小数大小的变化
小数点向右移动一位、两位、三位……原来的数就扩大10倍、100倍、1000倍……
小数点向左移动一位、两位、三位……原来的数就缩小10倍、100倍、1000倍……
如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足.
10.循环小数
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数.
如 0.5555…… 7.23838……
依次不断重复出现的数字叫做循环节.
循环小数的简便记法
0.5555…… 记作:0.5
7.23838……记作:7.238
.
..
10.循环小数
循环节从小数部分第一位开始的叫纯循环小数.如 0.5
循环节不是从小数部分第一位开始的叫混循环小数.如7.238
.
..
11.小数的分类
(1).按小数位数是有限还是无限分
(2).按小数的整数部分是否为0分
12.数的改写
一个较大的多位数,为了读写方便,常常把它改写成用
“万”或“亿”作单位的数.有时还可以根据需要,省略这个数某
一位后面的尾数,写成近似数.
把76450000改写成用“万”作单位的数是( )
把235800改写成用“万”作单位的数是( )
235800省略万位后面的尾数约为( )
把34562800000改写成用“亿”作单位的数后,保留两位
小数是( )
4.62975保留两位小数是:( )
4.62975保留三位小数是:( )
7645万
23.58万
24万
345.63亿
4.63
4.630
1.分数的意义和分数单位
单位“1”----
一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”
分 数----
分数各部分的名称:
分数单位----
把单位“1”平均分成若干份,表示其中的一份的数.
(表示平均分的份数)
(表示所取的份数)
把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数.
2.分数与除法
分数与除法的关系:
被除数÷除数=
(除数≠0)
把单位“1”平均分成9份,取其中的5份.
把5米平均分成9份,每份是( ),
每份是( )米.
3.分数大小的比较
★分母相同的两个分数,分子大的分数比较大.
★分子相同的两个分数,分母小的分数比较大.
<
>
<
>
★通分:先求出原来几个分母的最小公倍数,然后把各个
分数分别化成用这个最小公倍数作分母的分数.
<
4.分数的分类
真分数----
假分数----
分子比分母小的分数.
分子比分母大或者分子和分母
相等的分数.
真分数<1
假分数≥1
5.分数的基本性质
分数的分子和分母同时乘以或者除以相同的数
(零除外),分数的大小不变.
一个分数的分母不变,分子乘以3,则这个分数( )
如果分子不变,分母除以5,则这个分数( )
扩大3倍
扩大5倍
6.最简分数
*计算的结果,能约分的要约成最简分数;
假分数的,一般要化成带分数或整数.
*判断一个最简分数能不能化成有限小数:
分母中除了2和5以外,不含有其他的质因数,就能化成有限小数.
√
√
√
√
√
7.约分
约分------把一个分数化成和它相等,但分子和分母
都比较小的分数.
约分的方法:
1.用分子分母的公因数(1除外)逐次去除分子和
分母,直到得到最简分数为止.
2.用分子和分母的最大公因数去除分子和分母.
8.百分数的意义
表示一个数是另一个数的百分之几的数叫百分数.
百分数又叫百分率或百分比.
9.分数、小数、百分数的互化
小数
分数
百分数
0.25=( )
小数点向右移动两位,添上%
0.35%=( )
去掉%,小数点向左移动两位
先化成小数,再化成百分数
先写成分数,再约分
先用分数表示,再约分
分子除以分母
=
40%=
2
5
1
6
≈0.167=16.7%
1
4
=0.25=25%
1.2=
25%
0.0035
数的整除
1. 整除与除尽
2. 约数和倍数
3. 能被2.3.5整除的数的特征
4. 偶数和奇数
5. 质数和合数
6. 质因数和分解质因数
7. 最大公因数和最小公倍数
1. 整除与除尽
整除:
整数a除以整数b(b≠0),除得的商是整数而没有余数,
我们就说数a能被数b整除,或数b能整除a.
除尽:
数a除以数b(b≠0),除得的商是整数或是有限小数,
这就叫做除尽.
整除是除尽的一种特殊情况,整除也可以说是除尽,
但除尽不一定是整除.
区别:
2. 因数和倍数
如果a×b=c(a.b.c都不为0),那么a、b就叫做c的因数.c叫做a、b的倍数。(研究因数和倍数不考虑0)。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身.
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数.
因数和倍数是相互依存的
一个数既是本身的最大因数,也是本身最小的倍数。
3. 2.3.5倍数的特征
2的倍数的特征:
5的倍数的特征:
3的倍数的特征:
个位上是0,2,4,6,8,
个位上是0或5
各个数位上的数字的和是3的倍数
既是2的倍数,又是5的倍数的数的特征:
既是2的倍数,又是3,5的倍数的数的特征:
个位是0,而且各个位上的数字的和能被3整除.
注意:有一些数是7,9,11,13的倍数,但是不容易看出来,
这是大家在约分中容易忽略的.
个位是0
4. 偶数和奇数
一个自然数,不是奇数就是偶数
偶数:
是2的倍数的数叫做偶数
奇数:
不是2的倍数的数叫做奇数
偶数±偶数=( ) 奇数±奇数=( ) 偶数±奇数=( )
偶数×偶数=( ) 奇数×奇数=( ) 偶数×奇数=( )
偶数
偶数
偶数
偶数
奇数
奇数
最小的偶数是:
最小的奇数是:
0
1
5. 质数和合数
质数:
(素数)
只有1和它本身两个因数的数
合数:
除了1和它本身还有别的因数的数
1: 既不是质数也不是合数
最小的质数是:
最小的合数是:
2
4
要求:熟记100以内的质数表。
2是唯一的偶质数
6. 质因数和分解质因数
质因数:
分解质因数:
每一个合数都可以写成几个质数相乘的形式,
这几个质数叫做这个合数的质因数.
把一个合数用几个质因数相乘的形式表示出来.
叫做分解质因数.
分解质因数的方法:短除法
把30分解质因数正确的做法是( )
A.30=1×2 ×3 ×5
B.2 ×3 ×5=30
C.30=2×3×5
C
把30分解质因数
公因数,最大公因数:
几个数公有的因数,叫做这几个数的公因数;
其中最大的一个叫做这几个数的最大公因数.
例:( )是8和12的公因数,( )是8和12的最大公因数.
1,2,4
4
公倍数,最小公倍数:
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数.
例:( …)都是4和6的公倍数,( )是4和6的最小公倍数.
12,24,36
12
互质数:
公因数只有1的两个数叫做互质数.
⑴、两个数都是质数,这两个数一定互质.
⑵、相邻的两个数互质.
⑶、1和任何数都互质.
互质数的几种特殊情况
7. 最大公因数和最小公倍数
求最大公因数和最小公倍数
4和28 最大公因数是( ); 最小公倍数是( )
⑴.如果较小数是较大数的因数,那么较小数就是
这两个数的最大公因数;较大数就是这两个数的
最小公倍数.
4和15 最大公因数是( ); 最小公倍数是( )
⑵.如果两个数互质,它们的最大公因数就是1;
最小公倍数就是它们的积.
4
28
1
60
⑶.短除法
求24和36的最大公因数和最小公倍数
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
质数
数的运算1
——四则运算各部分之间的关系
各部分间的关系
加法 和=加数+加数 一个加数=和-另一个加数
减法 被减数-减数=差 减数=被减数-差 被减数=差+减数
乘法 因数×因数=积 一个因数=积÷另一个因数
除法 被除数÷除数=商 被除数=商×除数 除数=被除数÷商
四则运算定律和运算性质
加法交换律 a +b =b+a
加法结合律 a+b+c=a+(b+c)
乘法交换律 a×b=b×a
乘法结合律 a×b×c= a×(b×c )
乘法分配律 (a+b) ×c= a×c+ b×c
运算性质
减法的运算性质: a-(b+c)=a-b-c
a-b-c= a-(b+c)
除法的运算性质: a÷(b×c)= a÷b÷c
a÷b÷c= a÷(b×c)
0与1在四则运算中的特殊性
a+0=a a-0=a
a-a=0 a×0=0
a×0=0 a×1=a
a÷1=a 0÷a=0
1÷a= a÷a=1
四则运算的顺序
1、 四则运算分为两级:加法和减法为第一级运算,乘法和除法为第二级运算
2、 四则混合运算的顺序:
(1)在没有括号的算式里,如果只有同级计算,从左往右按顺序计算;如果有两级计算,要先算第二级计算,再算第一级计算。
(2)有括号的先算小括号里面的,再算中括号里面的,最后算括号外面的。
数的运算2:解决问题
常用的两种分析方法:
1、综合法:从已知数量和已知数量关系入手,利用已知信息看能解决什么问题,直到求出未知数量的解题方法。
2、分析法:从所求的问题出发,逐步找出解答问题所需的条件,依次推导,直到问题得到解决。
