人教版数学八年级下册:19.2.1 正比例函数 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级下册:19.2.1 正比例函数 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 20:29:47 | ||
图片预览








文档简介
课件25张PPT。
人教版 八年级数学下册
第19章 一次函数
19.2.1 正比例函数1.理解正比例函数的概念.
2.会求正比例函数的解析式,能利用正比例函数解决简单的实际问题.
3.理解正比例函数的图象的特点,会利用两点(法)画正比例函数的图象.
4.掌握正比例函数的性质,并能灵活运用性质解答有关问题.学习目标问题:2011年开始运营的京沪高速铁路全长1318km,设列车的平均速度为300km/h,考虑以下问题:
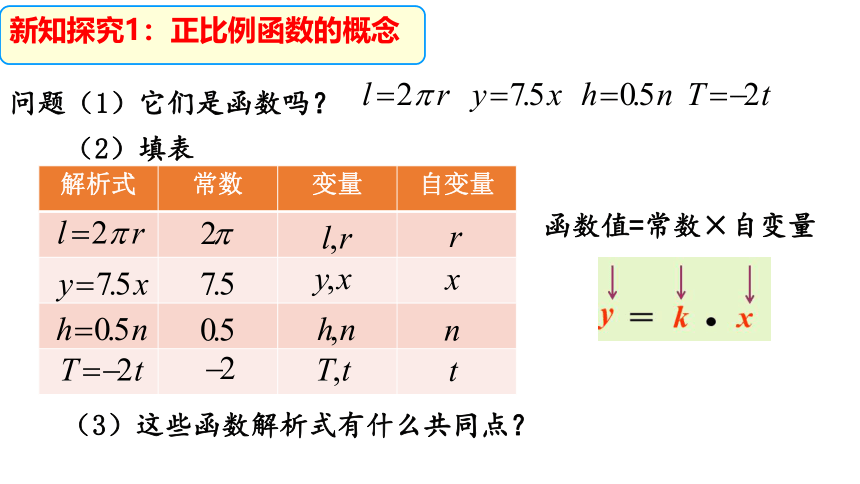
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需要多少小时(结果保留小数点后一位)?创设情境(2)京沪高铁的行程 (单位:km)与运行时间 (单位:h)之间有何数量关系?(3)京沪高铁从北京南站出发2.5小时后,是否已经过了距离始发站1100km的南京南站? 1318÷300≈4.4h 大约要4.4小时 ( )2.5x300=750km<1100km 所以还没有经过南京南站 问题2:函数解析式有什么特点?问题1:观察 , 是 的函数吗?说出常数和自变量.(2)函数=常数×自变量创设情境(1)是;常数:300,自变量t.生活中有很多类似的函数,请同学们思考下面的问题.(1)圆的周长 随半径 的大小变化而变化.思考:下列问题中的变量对应规律可用怎样的关系式表示?(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度 (单位:cm)随这些练习本的本数 的变化而变化.(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度 (单位:℃)随冷冻时间 (单位:分)的变化而变化.(2)市场上苹果每千克7.5元,买苹果所需的钱数 (单位:元)随购买的数量 (单位:千克)的变化而变化.新知探究1:正比例函数的概念(1)(2)(3)(4)(3)这些函数解析式有什么共同点?思考归纳函数值=常数×自变量新知探究1:正比例函数的概念问题(1)它们是函数吗? (2)填表 正比例函数解析式 ( )的结构特征:
① 是常数 , .
② 的次数是1.
③自变量与常数的乘积.一般地,形如 ( 是常数, )的函数,叫做正比例函数,其中 叫做比例系数.新知探究1:正比例函数的概念1 判断下列各题中所指的两个量是否成正比例。
(是在括号内打“ ” ,不是在括号内打“ ”)(1)圆周长C与半径r( )
(2)圆面积S与半径r ( )
(3)在匀速运动中的路程s与时间t ( )做一做2. 若一个正比例函数的比例系数是4,
则它的解析式为__________.3.正比例函数 中,当 时,
,则它的解析式为_________.y = 4xy = 5x做一做新知探究2:待定系数法通过先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.例 已知正比例函数的图象过点(-3,-9),求这个正比例函数的解析式.解:设函数的解析式为 ,将 ,
代入,解得
所以这个正比例函数的解析式为 .新知探究2:待定系数法新知探究2:待定系数法练习 已知 与 成正比例,且当
时, ,则当 时, ____.解:根据题意,设
将 , 代入解得
所以
将 代入上式,解得 7
我们现在已经知道了正比例函数关系式的特点,那么它的图象有什么特征呢?画出下列正比例函数的图象
(1) 和 (2) 和 新知探究3:正比例函数的图象及性质 友情提示:
画函数图象的步骤为:列表、描点、连线
解:1、列表2、描点3、连线(1) 和 新知探究3:正比例函数的图象及性质
解:1、列表2、描点3、连线(2) 和 新知探究3:正比例函数的图象及性质
比较上面几个正比例函数图像,它们有什么相同点和不同点?相同点:都是经过原点的直线不同点:(1)位置不同。
(2)从左到右变化趋势不同。
当 时,它的图象经过第_____象限.
当 时,它的图象经过第_____象限.一、三二、四 从左到右图象上升;
增大时, 的值也增大,
即 随 的增大而增大.从左到右图象下降;
增大时, 的值反而减小,
即 随 的增大而减小.新知探究3:正比例函数的图象及性质当 时,直线 经过第一、三象限, 随 的增大而增大;
当 时,直线 经过第二、四象限, 随 的增大而减小.
正比例函数 ( 是常数且 ) 的图象是经过原点的一条直线.我们称它为直线 .新知探究3:正比例函数的图象及性质
思考:经过原点和(1,k)的直线是哪个函数的图象?如何画正比例函数的图像最简单?新知探究3:正比例函数的图象及性质所以,画正比例函数图象时,只需描两个点,然后过这两个点画一条直线.因为正比例函数的图像是一条直线,而两点确定一条直线,它一定经过点 和 . (0,0)(1,k)两点法: (0,0) , (1,k)新知探究3:正比例函数的图象及性质1. 用你认为最简单的方法画出下列函数的图象:
(1) ;(2)做一做2. 关于函数 ,下列判断正确的是( )
A、图象必过点(-1,-2)
B、图象 经过一、三象限
C、 随 的增大而减小
D 、不论 为何值都有C做一做3. 已知正比例函数 ,若 随 的增大而增大,则 的取值范围是 ( )
A. B. C. D. 4. 如果正比例函数 的图象经过点(3,-6),那么
等于______, 随 的增大而_________.D-2减小做一做 已知 与 成正比例,且 时, .
求 与 之间的函数关系式;
(2) 如果 的取值范围是 ,求 的取值范围.能力提升解:(1) 根据题意,设
将 , 代入解得
所以 ,即
(2) 因为 ,所以 随 的增大而增大.
又当 时, ;当 时, .
所以 的取值范围是 .正比例函数正比例函数的概念和解析式.函数 ( 是不等于零的常数)叫做正比例函数. 为比例系数.可用已知的比例系数求解析式或用待定系数法求解析式正比例函数的图象.正比例函数的图象是经过原点的一条直线正比例函数的性质.当 时 ,直线 经过第一、三象限, 随 的增大而增大; 当 时,直 线 经过第二、四象限, 随 的增大而减小课堂小结必做题:教材87页练习
选做题:98页习题19.2第2题课后作业
人教版 八年级数学下册
第19章 一次函数
19.2.1 正比例函数1.理解正比例函数的概念.
2.会求正比例函数的解析式,能利用正比例函数解决简单的实际问题.
3.理解正比例函数的图象的特点,会利用两点(法)画正比例函数的图象.
4.掌握正比例函数的性质,并能灵活运用性质解答有关问题.学习目标问题:2011年开始运营的京沪高速铁路全长1318km,设列车的平均速度为300km/h,考虑以下问题:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需要多少小时(结果保留小数点后一位)?创设情境(2)京沪高铁的行程 (单位:km)与运行时间 (单位:h)之间有何数量关系?(3)京沪高铁从北京南站出发2.5小时后,是否已经过了距离始发站1100km的南京南站? 1318÷300≈4.4h 大约要4.4小时 ( )2.5x300=750km<1100km 所以还没有经过南京南站 问题2:函数解析式有什么特点?问题1:观察 , 是 的函数吗?说出常数和自变量.(2)函数=常数×自变量创设情境(1)是;常数:300,自变量t.生活中有很多类似的函数,请同学们思考下面的问题.(1)圆的周长 随半径 的大小变化而变化.思考:下列问题中的变量对应规律可用怎样的关系式表示?(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度 (单位:cm)随这些练习本的本数 的变化而变化.(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度 (单位:℃)随冷冻时间 (单位:分)的变化而变化.(2)市场上苹果每千克7.5元,买苹果所需的钱数 (单位:元)随购买的数量 (单位:千克)的变化而变化.新知探究1:正比例函数的概念(1)(2)(3)(4)(3)这些函数解析式有什么共同点?思考归纳函数值=常数×自变量新知探究1:正比例函数的概念问题(1)它们是函数吗? (2)填表 正比例函数解析式 ( )的结构特征:
① 是常数 , .
② 的次数是1.
③自变量与常数的乘积.一般地,形如 ( 是常数, )的函数,叫做正比例函数,其中 叫做比例系数.新知探究1:正比例函数的概念1 判断下列各题中所指的两个量是否成正比例。
(是在括号内打“ ” ,不是在括号内打“ ”)(1)圆周长C与半径r( )
(2)圆面积S与半径r ( )
(3)在匀速运动中的路程s与时间t ( )做一做2. 若一个正比例函数的比例系数是4,
则它的解析式为__________.3.正比例函数 中,当 时,
,则它的解析式为_________.y = 4xy = 5x做一做新知探究2:待定系数法通过先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.例 已知正比例函数的图象过点(-3,-9),求这个正比例函数的解析式.解:设函数的解析式为 ,将 ,
代入,解得
所以这个正比例函数的解析式为 .新知探究2:待定系数法新知探究2:待定系数法练习 已知 与 成正比例,且当
时, ,则当 时, ____.解:根据题意,设
将 , 代入解得
所以
将 代入上式,解得 7
我们现在已经知道了正比例函数关系式的特点,那么它的图象有什么特征呢?画出下列正比例函数的图象
(1) 和 (2) 和 新知探究3:正比例函数的图象及性质 友情提示:
画函数图象的步骤为:列表、描点、连线
解:1、列表2、描点3、连线(1) 和 新知探究3:正比例函数的图象及性质
解:1、列表2、描点3、连线(2) 和 新知探究3:正比例函数的图象及性质
比较上面几个正比例函数图像,它们有什么相同点和不同点?相同点:都是经过原点的直线不同点:(1)位置不同。
(2)从左到右变化趋势不同。
当 时,它的图象经过第_____象限.
当 时,它的图象经过第_____象限.一、三二、四 从左到右图象上升;
增大时, 的值也增大,
即 随 的增大而增大.从左到右图象下降;
增大时, 的值反而减小,
即 随 的增大而减小.新知探究3:正比例函数的图象及性质当 时,直线 经过第一、三象限, 随 的增大而增大;
当 时,直线 经过第二、四象限, 随 的增大而减小.
正比例函数 ( 是常数且 ) 的图象是经过原点的一条直线.我们称它为直线 .新知探究3:正比例函数的图象及性质
思考:经过原点和(1,k)的直线是哪个函数的图象?如何画正比例函数的图像最简单?新知探究3:正比例函数的图象及性质所以,画正比例函数图象时,只需描两个点,然后过这两个点画一条直线.因为正比例函数的图像是一条直线,而两点确定一条直线,它一定经过点 和 . (0,0)(1,k)两点法: (0,0) , (1,k)新知探究3:正比例函数的图象及性质1. 用你认为最简单的方法画出下列函数的图象:
(1) ;(2)做一做2. 关于函数 ,下列判断正确的是( )
A、图象必过点(-1,-2)
B、图象 经过一、三象限
C、 随 的增大而减小
D 、不论 为何值都有C做一做3. 已知正比例函数 ,若 随 的增大而增大,则 的取值范围是 ( )
A. B. C. D. 4. 如果正比例函数 的图象经过点(3,-6),那么
等于______, 随 的增大而_________.D-2减小做一做 已知 与 成正比例,且 时, .
求 与 之间的函数关系式;
(2) 如果 的取值范围是 ,求 的取值范围.能力提升解:(1) 根据题意,设
将 , 代入解得
所以 ,即
(2) 因为 ,所以 随 的增大而增大.
又当 时, ;当 时, .
所以 的取值范围是 .正比例函数正比例函数的概念和解析式.函数 ( 是不等于零的常数)叫做正比例函数. 为比例系数.可用已知的比例系数求解析式或用待定系数法求解析式正比例函数的图象.正比例函数的图象是经过原点的一条直线正比例函数的性质.当 时 ,直线 经过第一、三象限, 随 的增大而增大; 当 时,直 线 经过第二、四象限, 随 的增大而减小课堂小结必做题:教材87页练习
选做题:98页习题19.2第2题课后作业
