人教版八年级数学下册17.2 勾股定理的逆定理同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册17.2 勾股定理的逆定理同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 114.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 21:12:18 | ||
图片预览


文档简介
17.2 勾股定理的逆定理
选择题
1.△ABC的三边为a,b,c,且(a+b)(a﹣b)=c2,则(???? )
A.△ABC是锐角三角形??? ? B.c边的对角是直角
C.△ABC是钝角三角形??? ? D.a边的对角是直角
2.三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )
A.等边三角形?? B.钝角三角形?? C.直角三角形?? D.锐角三角形
3.下面各选项给出的是三角形中各边的长度的平方比,其中不是直角三角形的是( ).
A.1∶1∶2 B.1∶3∶4
C.9∶25∶26 D.25∶144∶169
4.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2-c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
5. 如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,则MN=( )
A. B. C. D.
如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A.75 B.100 C.120 D.125
7.如图,四边形ABCD中,∠B=∠D=90°,∠A=45°,AB=3,CD=1,则BC的长为(???? )
A.3??? B.2?? C.???D.
8.如图,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
A. 24平方米???? B. 26平方米??? C. 28平方米? D. 30平方米
9.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成各选项所示的两个直角三角形,其中正确的是( )
10.已知四个三角形分别满足下列条件:①三角形的三边之比为1:1:;②三角形的三边分别是9、40、41;③三角形三内角之比为1:2:3;④三角形一边上的中线等于这边的一半。其中直角三角形有( )个。
A.4 B.3 C.2 D.1
填空题
11.已知a.b.c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为?????? .?
12.某住宅小区有一块草坪如图所示,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是??????? .
13.△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为______,此三角形为______.
14.一个三角形三条边的比为5:12:13,且周长为60cm,它的面积是 。
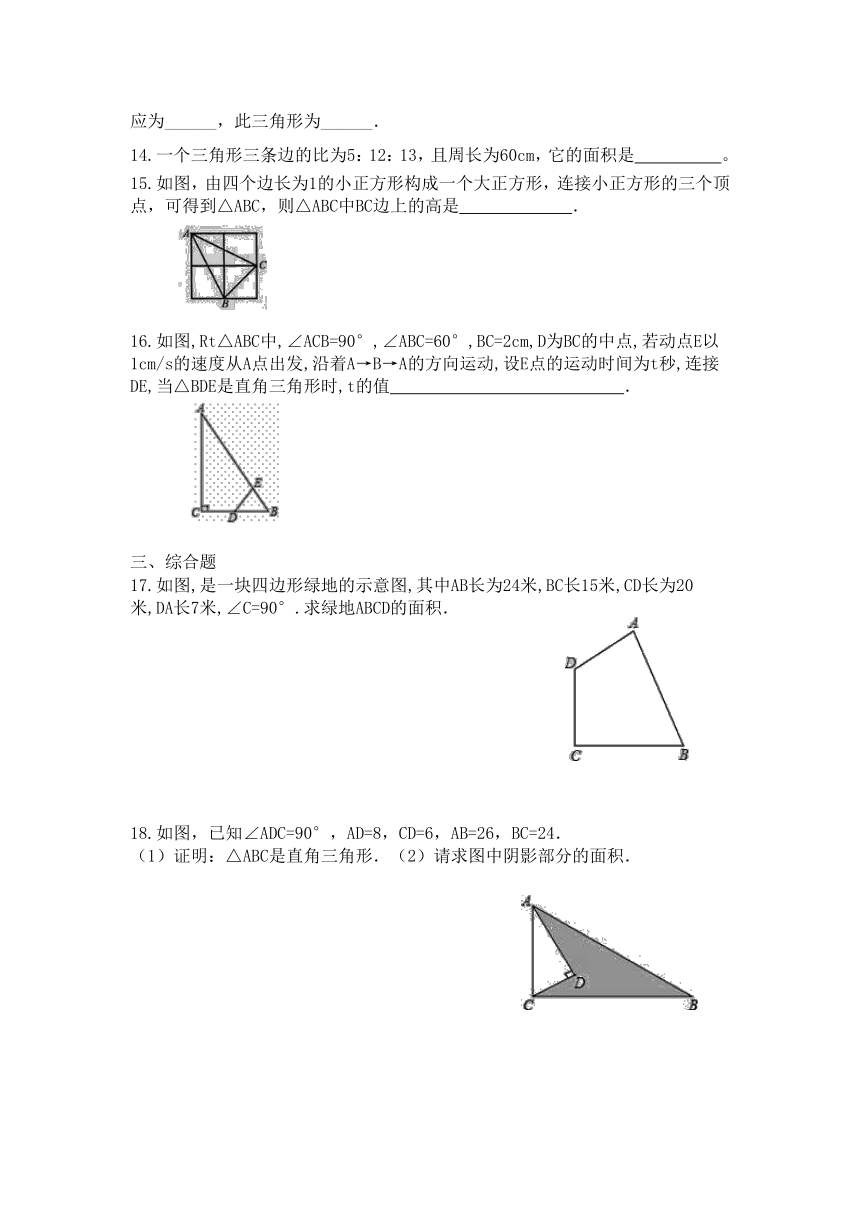
15.如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是?????? .
16.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值????????????? .
综合题
17.如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°.求绿地ABCD的面积.
18.如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.
19.已知a、b、c是△ABC的三边,且a2c2-b2c2=a4-b4,试判断三角形的形状.
20.如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?
17.2 勾股定理的逆定理
答案
选择题
1.D 2.C 3.B 4.C 5.C 6.B 7.D 8.A 9.C 10.A
二、填空题
11.直角三角形
12.36
13.13,直角三角形
14.120cm2
2或6或3.5或4.5
三、综合题
17.解:连接BD.如图所示.∵∠C=90°,BC=15米,CD=20米,∴BD===25(米).在△ABD中,∵BD=25米,AB=24米,DA=7米,242+72=252,即AB2+AD2=BD2,∴△ABD是直角三角形.∴S四边形ABCD=S△ABD+S△BCD=AB?AD+BC?CD=×24×7+×15×20=84+150=234(平方米).即绿地ABCD的面积为234平方米.
18.(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,
∴AC2=AD2+CD2=82+62=100,
∴AC=10.在△ABC中,
∵AC2+BC2=102+242=676,AB2=262=676,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
解:S阴影=SRt△ABC﹣SRt△ACD=×10×24﹣×8×6=96.
19.等腰三角形或直角三角形.
提示:原式可变形为(a2-b2)(a2+b2-c2)=0.
20.解:BM=8×2=16海里,
BP=15×2=30海里,
在△BMP中,BM2+BP2=256+900=1156,PM2=1156,
BM2+BP2=PM2,
∴∠MBP=90°,
180°-90°-60°=30°,
故乙船沿南偏东30°方向航行。
选择题
1.△ABC的三边为a,b,c,且(a+b)(a﹣b)=c2,则(???? )
A.△ABC是锐角三角形??? ? B.c边的对角是直角
C.△ABC是钝角三角形??? ? D.a边的对角是直角
2.三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )
A.等边三角形?? B.钝角三角形?? C.直角三角形?? D.锐角三角形
3.下面各选项给出的是三角形中各边的长度的平方比,其中不是直角三角形的是( ).
A.1∶1∶2 B.1∶3∶4
C.9∶25∶26 D.25∶144∶169
4.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2-c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
5. 如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,则MN=( )
A. B. C. D.
如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A.75 B.100 C.120 D.125
7.如图,四边形ABCD中,∠B=∠D=90°,∠A=45°,AB=3,CD=1,则BC的长为(???? )
A.3??? B.2?? C.???D.
8.如图,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
A. 24平方米???? B. 26平方米??? C. 28平方米? D. 30平方米
9.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成各选项所示的两个直角三角形,其中正确的是( )
10.已知四个三角形分别满足下列条件:①三角形的三边之比为1:1:;②三角形的三边分别是9、40、41;③三角形三内角之比为1:2:3;④三角形一边上的中线等于这边的一半。其中直角三角形有( )个。
A.4 B.3 C.2 D.1
填空题
11.已知a.b.c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为?????? .?
12.某住宅小区有一块草坪如图所示,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是??????? .
13.△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为______,此三角形为______.
14.一个三角形三条边的比为5:12:13,且周长为60cm,它的面积是 。
15.如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是?????? .
16.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值????????????? .
综合题
17.如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°.求绿地ABCD的面积.
18.如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.
19.已知a、b、c是△ABC的三边,且a2c2-b2c2=a4-b4,试判断三角形的形状.
20.如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?
17.2 勾股定理的逆定理
答案
选择题
1.D 2.C 3.B 4.C 5.C 6.B 7.D 8.A 9.C 10.A
二、填空题
11.直角三角形
12.36
13.13,直角三角形
14.120cm2
2或6或3.5或4.5
三、综合题
17.解:连接BD.如图所示.∵∠C=90°,BC=15米,CD=20米,∴BD===25(米).在△ABD中,∵BD=25米,AB=24米,DA=7米,242+72=252,即AB2+AD2=BD2,∴△ABD是直角三角形.∴S四边形ABCD=S△ABD+S△BCD=AB?AD+BC?CD=×24×7+×15×20=84+150=234(平方米).即绿地ABCD的面积为234平方米.
18.(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,
∴AC2=AD2+CD2=82+62=100,
∴AC=10.在△ABC中,
∵AC2+BC2=102+242=676,AB2=262=676,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
解:S阴影=SRt△ABC﹣SRt△ACD=×10×24﹣×8×6=96.
19.等腰三角形或直角三角形.
提示:原式可变形为(a2-b2)(a2+b2-c2)=0.
20.解:BM=8×2=16海里,
BP=15×2=30海里,
在△BMP中,BM2+BP2=256+900=1156,PM2=1156,
BM2+BP2=PM2,
∴∠MBP=90°,
180°-90°-60°=30°,
故乙船沿南偏东30°方向航行。
