人教版八年级数学下册17.1勾股定理同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册17.1勾股定理同步练习(含答案) | 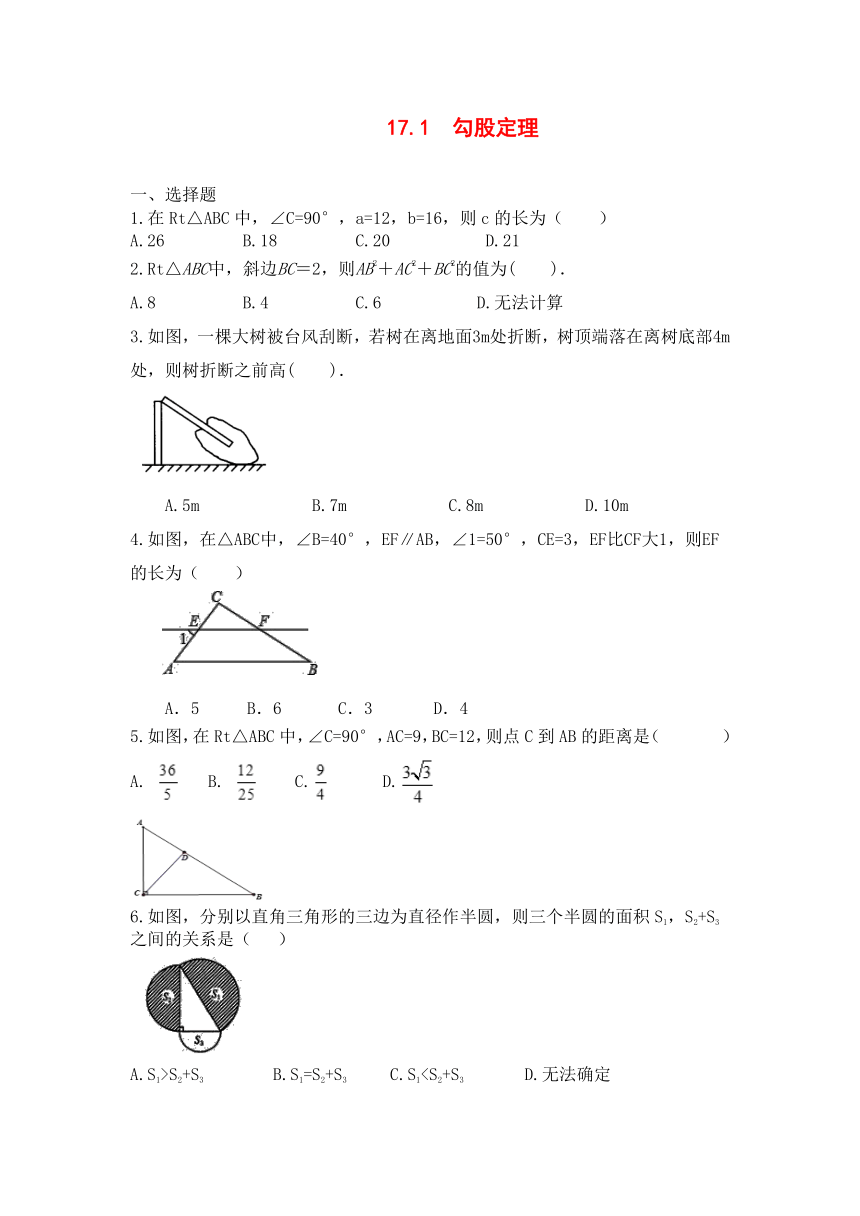 | |
| 格式 | zip | ||
| 文件大小 | 119.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 21:16:06 | ||
图片预览



文档简介
17.1 勾股定理
选择题
1.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( )
A.26?? ? B.18?? ? C.20? ?? ? D.21
2.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( ).
A.8 B.4 C.6 D.无法计算
3.如图,一棵大树被台风刮断,若树在离地面3m处折断,树顶端落在离树底部4m处,则树折断之前高( ).
A.5m B.7m C.8m D.10m
4.如图,在△ABC中,∠B=40°,EF∥AB,∠1=50°,CE=3,EF比CF大1,则EF的长为( )
A.5 B.6 C.3 D.4
5.如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( ? ?)
A. B. C. D.
6.如图,分别以直角三角形的三边为直径作半圆,则三个半圆的面积S1,S2+S3之间的关系是(? )
A.S1>S2+S3????B.S1=S2+S3?? C.S17.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则线段B'F的长为 ( )
A. B. C. D.
8.如图,从台阶的下端点B到上端点A的直线距离为( ).
A. B.
C. D.
9.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
10.如图,一个无盖的正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从盒外的D点沿正方体的盒壁爬到盒内的M点(盒壁的厚度不计),蚂蚁爬行的最短距离是(? ?)
A. B. C. D.
填空题
在直角三角形中,一条直角边为11cm,另两边是两个连续自然数,则此直角三角形的周长为______.
12.长为4 m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了______m.
13.如图中的螺旋形由一系列含30°的直角三角形组成,其序号依次为①、②、③、④、⑤…,则第7个直角三角形的斜边长为 。
14.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为________________。
15..我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3. 若S1+S2+S3=15,则S2的值是 .
16.如图,在 Rt△ABC 中,∠C=90°,BC=3 cm,AC= 4 cm,按图中所示方法将△BCD沿BD折叠,使点C 落在AB边的C'点处,那么△ADC'的面积是 .
综合题
17.如图,在高为3米,斜坡长为5米的楼梯表面铺地毯,则地毯的长度至少需要多少米?若楼梯宽2米,地毯每平方米30元,那么这块地毯需花多少元?
18.如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积。
19.A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
20.将长为2.5米的梯子AC斜靠在墙上,梯子的底部离墙的底端1.5米(即图中BC的长).
(1)求梯子的顶端与地面的距离;
(2)若梯子顶端A下滑1.3米,那么梯子底端C向左移动了多少米?
17.1 勾股定理
答案
选择题
1.C 2.A 3.C 4.A 5.A 6.B 7.B 8.A 9.A 10.D
二、填空题
11.132cm
45°
5
三、综合题
17.7米,420元.
18.
19.解:(1)如图,由A点向BF作垂线,垂足为C,在Rt△ABC中,∠ABC=30°,AB=320km,则AC=160km.∵160<200,∴A城要受台风影响.
(2)设BF上点D,DA=200千米,另一点G,有AG=200千米.∵DA=AG,∴△ADG是等腰三角形.∵AC⊥BF,∴AC是DG的垂直平分线,CD=GC.在Rt△ADC中,DA=200千米,AC=160千米,由勾股定理得CD==120千米,
则DG=2DC=240千米,∴遭受台风影响的时间是240÷40=6(小时).
20.(1)AB===2(米).
??(2) 设点A下滑到点,点C移动到点,则=2-1.3=0.7(米),==2.4(米),∴=0.9(米).
选择题
1.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( )
A.26?? ? B.18?? ? C.20? ?? ? D.21
2.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( ).
A.8 B.4 C.6 D.无法计算
3.如图,一棵大树被台风刮断,若树在离地面3m处折断,树顶端落在离树底部4m处,则树折断之前高( ).
A.5m B.7m C.8m D.10m
4.如图,在△ABC中,∠B=40°,EF∥AB,∠1=50°,CE=3,EF比CF大1,则EF的长为( )
A.5 B.6 C.3 D.4
5.如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( ? ?)
A. B. C. D.
6.如图,分别以直角三角形的三边为直径作半圆,则三个半圆的面积S1,S2+S3之间的关系是(? )
A.S1>S2+S3????B.S1=S2+S3?? C.S1
A. B. C. D.
8.如图,从台阶的下端点B到上端点A的直线距离为( ).
A. B.
C. D.
9.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
10.如图,一个无盖的正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从盒外的D点沿正方体的盒壁爬到盒内的M点(盒壁的厚度不计),蚂蚁爬行的最短距离是(? ?)
A. B. C. D.
填空题
在直角三角形中,一条直角边为11cm,另两边是两个连续自然数,则此直角三角形的周长为______.
12.长为4 m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了______m.
13.如图中的螺旋形由一系列含30°的直角三角形组成,其序号依次为①、②、③、④、⑤…,则第7个直角三角形的斜边长为 。
14.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为________________。
15..我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3. 若S1+S2+S3=15,则S2的值是 .
16.如图,在 Rt△ABC 中,∠C=90°,BC=3 cm,AC= 4 cm,按图中所示方法将△BCD沿BD折叠,使点C 落在AB边的C'点处,那么△ADC'的面积是 .
综合题
17.如图,在高为3米,斜坡长为5米的楼梯表面铺地毯,则地毯的长度至少需要多少米?若楼梯宽2米,地毯每平方米30元,那么这块地毯需花多少元?
18.如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积。
19.A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
20.将长为2.5米的梯子AC斜靠在墙上,梯子的底部离墙的底端1.5米(即图中BC的长).
(1)求梯子的顶端与地面的距离;
(2)若梯子顶端A下滑1.3米,那么梯子底端C向左移动了多少米?
17.1 勾股定理
答案
选择题
1.C 2.A 3.C 4.A 5.A 6.B 7.B 8.A 9.A 10.D
二、填空题
11.132cm
45°
5
三、综合题
17.7米,420元.
18.
19.解:(1)如图,由A点向BF作垂线,垂足为C,在Rt△ABC中,∠ABC=30°,AB=320km,则AC=160km.∵160<200,∴A城要受台风影响.
(2)设BF上点D,DA=200千米,另一点G,有AG=200千米.∵DA=AG,∴△ADG是等腰三角形.∵AC⊥BF,∴AC是DG的垂直平分线,CD=GC.在Rt△ADC中,DA=200千米,AC=160千米,由勾股定理得CD==120千米,
则DG=2DC=240千米,∴遭受台风影响的时间是240÷40=6(小时).
20.(1)AB===2(米).
??(2) 设点A下滑到点,点C移动到点,则=2-1.3=0.7(米),==2.4(米),∴=0.9(米).
