沪教版数学七年级第二学期第十四章 三角形 单元练习(含答案)
文档属性
| 名称 | 沪教版数学七年级第二学期第十四章 三角形 单元练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 21:52:57 | ||
图片预览


文档简介
第十四章 三角形
一、单选题
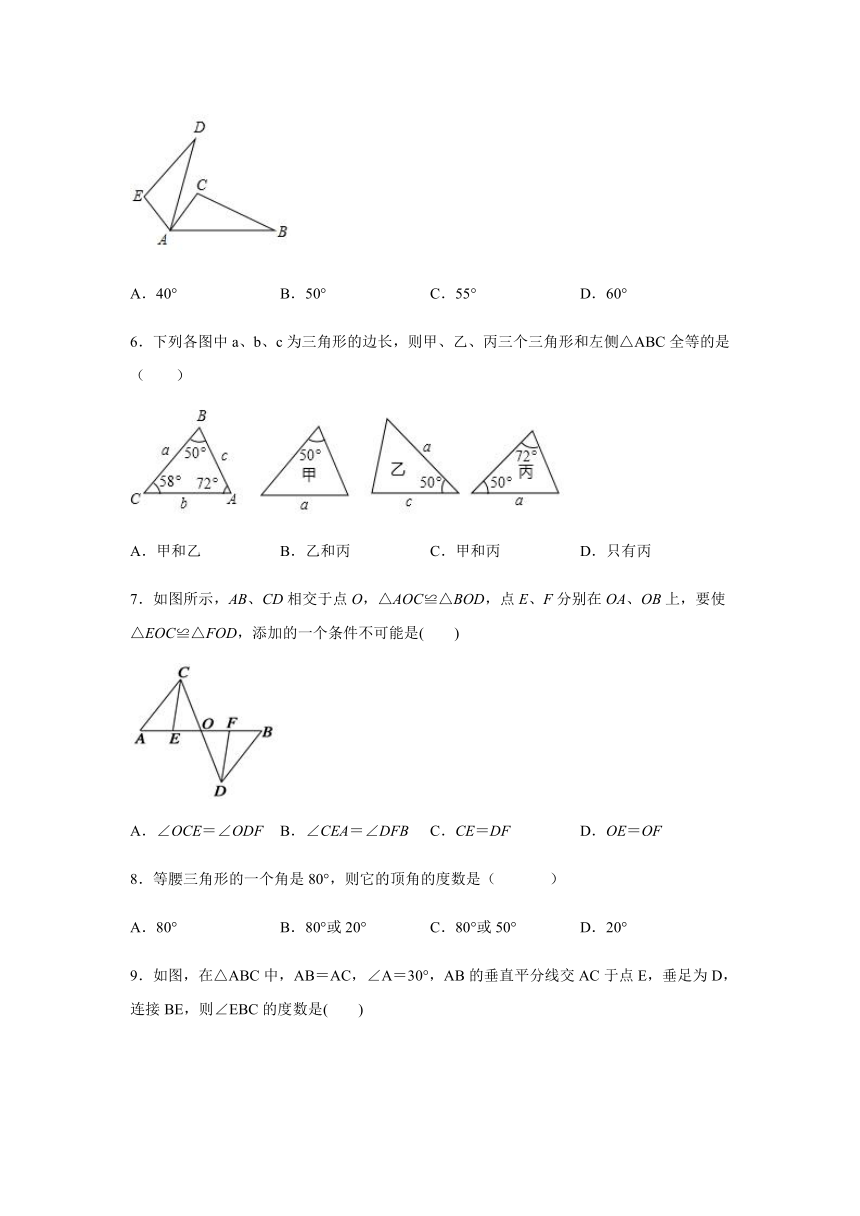
1.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
2.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点, 且△ABC的面积为4cm2,则△BEF的面积等于( )
A.2cm2 B.1cm2 C.0.5 cm2 D.0.25 cm2
3.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE度数为( ).
A.45° B.64° C.71° D.80°.
4.如图,△ABC≌△CDA,若AB=3,BC=4,则四边形ABCD的周长是( )
A.14 B.11 C.16 D.12
5.如图,△ABC≌△ADE,且∠B=25°,∠E=105°,∠DAC=10°,则∠EAC等于( )
A.40° B.50° C.55° D.60°
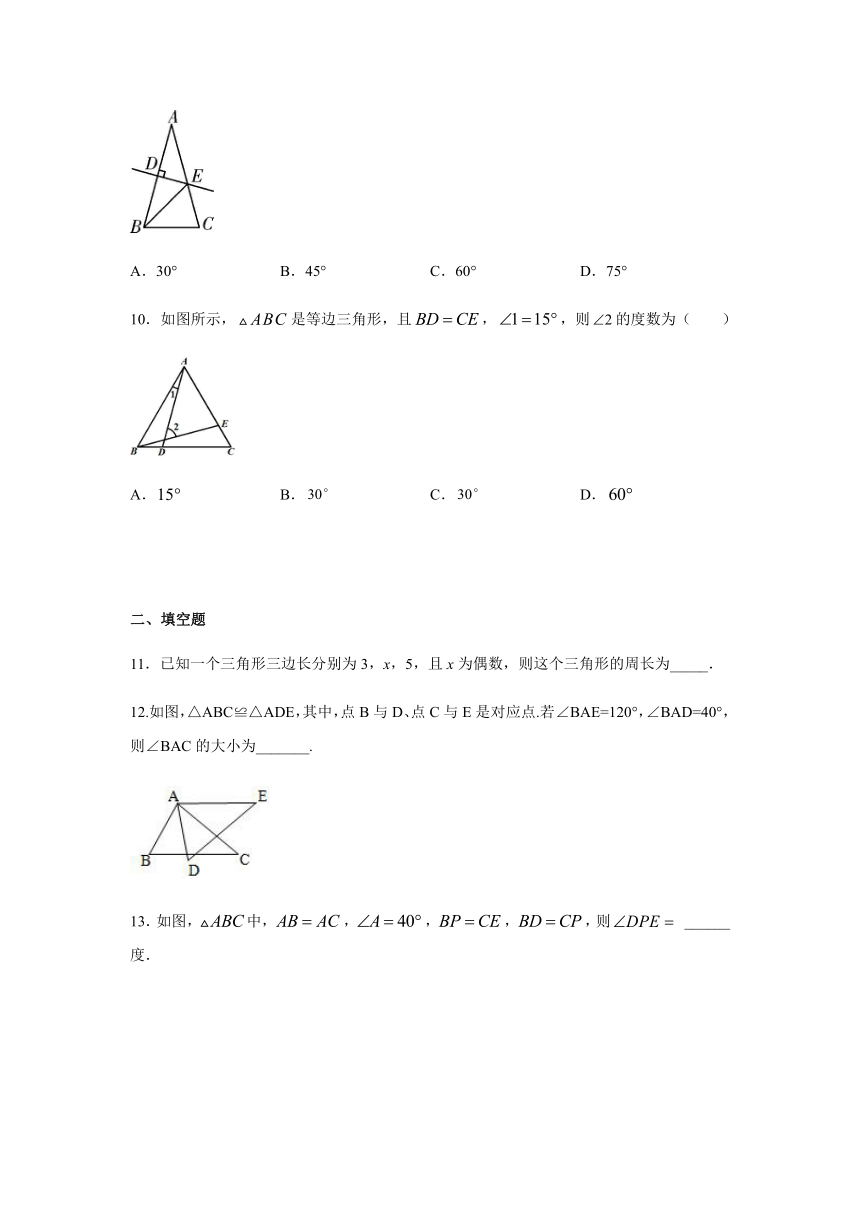
6.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
7.如图所示,AB、CD相交于点O,△AOC≌△BOD,点E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可能是( )
A.∠OCE=∠ODF B.∠CEA=∠DFB C.CE=DF D.OE=OF
8.等腰三角形的一个角是80°,则它的顶角的度数是( )
A.80° B.80°或20° C.80°或50° D.20°
9.如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线交AC于点E,垂足为D,连接BE,则∠EBC的度数是( )
A.30° B.45° C.60° D.75°
10.如图所示,是等边三角形,且,,则的度数为( )
A. B. C. D.
二、填空题
11.已知一个三角形三边长分别为3,x,5,且x为偶数,则这个三角形的周长为_____.
12.如图,△ABC≌△ADE,其中,点B与D、点C与E是对应点.若∠BAE=120°,∠BAD=40°,则∠BAC的大小为_______.
13.如图,中,,,,,则 ______ 度.
14.如图,在中,,,在上取点,延长到,使得;在上取一点,延长到,使得;…,按此做法进行下去,第n个等腰三角形的底角的度数为__________.
三、解答题
15.如图,已知,在△ABC中,∠C=∠ABC,BE⊥AC,∠DBE=60°,求∠C的度数.
16.如图,在四边形ABCD中,点E是对角线BD上的一点,EA⊥AB,EC⊥BC,且EA=EC.求证:AD=CD.
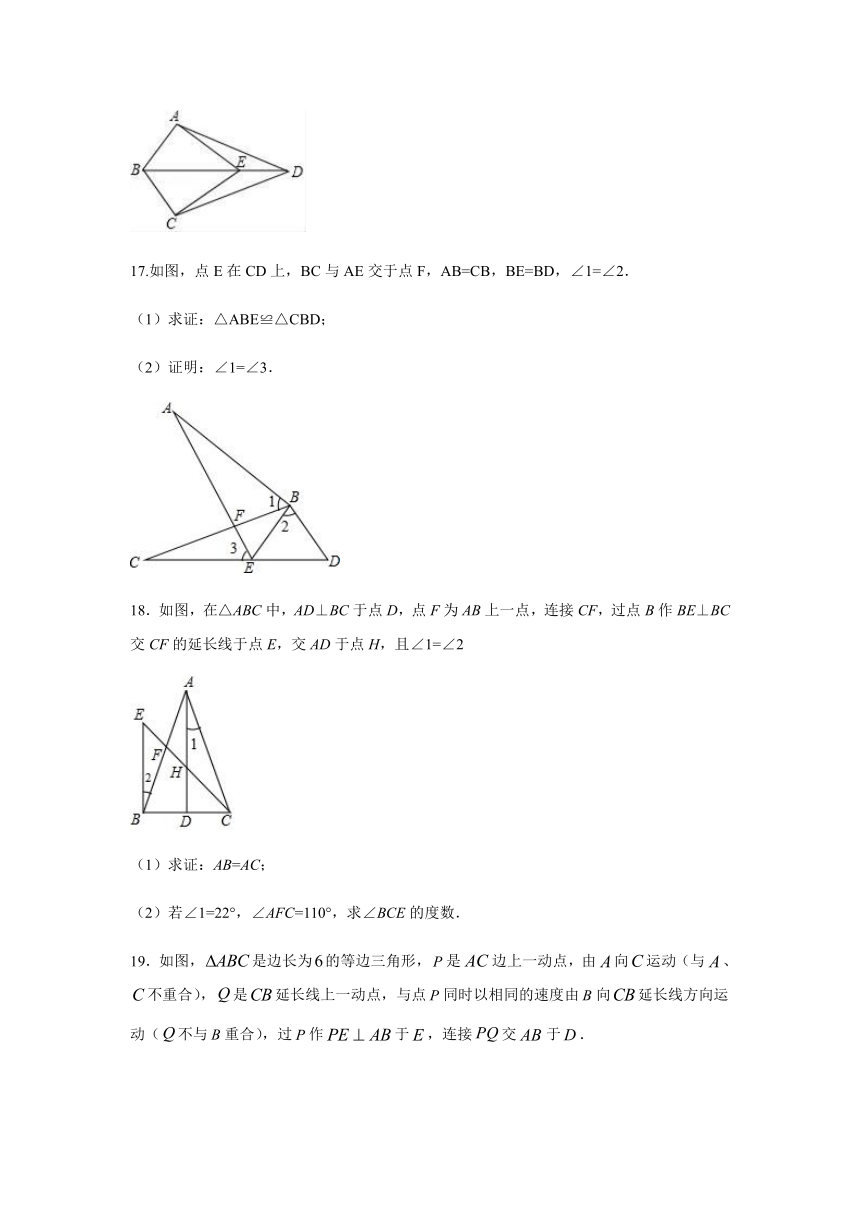
17.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
18.如图,在△ABC中,AD⊥BC于点D,点F为AB上一点,连接CF,过点B作BE⊥BC交CF的延长线于点E,交AD于点H,且∠1=∠2
(1)求证:AB=AC;
(2)若∠1=22°,∠AFC=110°,求∠BCE的度数.
19.如图,是边长为的等边三角形,是边上一动点,由向运动(与、不重合),是延长线上一动点,与点同时以相同的速度由向延长线方向运动(不与重合),过作于,连接交于.
(1)若时,求的长;
(2)当时,求的长;
(3)在运动过程中线段的长是否发生变化?如果不变,求出线段的长;如果发生变化,请说明理由
答案
1.C
2.B
3.C
4.A
5.D
6.B
7.C
8.B
9.B
10.D
11.12或14
12.80°
13.70
14..
15.∵BE⊥AC,
∴∠AEB=90°,
∵∠DBE=60°,
∴∠A=90°-60°=30°,
∴∠C=∠ABC=(180°-30°)=75°.
16.∵EA⊥AB,EC⊥BC,
∴∠EAB=∠ECB=90°,
在Rt△EAB与Rt△ECB中
,
∴Rt△EAB≌Rt△ECB,
∴AB=CB,∠ABE=∠CBE,
∵BD=BD,
在△ABD与△CBD中
,
∴△ABD≌△CBD,
∴AD=CD.
17.,
,即,
在和中,
,
≌;
≌,
,
,
18.(1)证明:∵EB⊥BC,AD⊥BC,
∴EB∥AD,
∴∠2=∠BAD,
∵∠1=∠2,
∴∠BAD=∠1,
∵∠1+∠ACD=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠ACB,
∴AB=AC.
(2)解:∵∠2=∠1=22°,∠EBC=90°,
∴∠FBC=68°,
∵∠AFC=∠FBC+∠ECB,
∴∠ECB=110°-68°=42°.
19.(1)∵△ABC是等边三角形,
∴∠A=60,
∵PE⊥AB,
∴∠APE=30,
∵AE=1,∠APE=30,PE⊥AB,
∴AP=2AE=2;
(2)解:过P作PF∥QC,
则△AFP是等边三角形,
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30,
∴BD=DF=FA=AB=2,
∴AP=2;
(3)解:由(2)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=BF+FA=AB=3为定值,即DE的长不变
一、单选题
1.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
2.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点, 且△ABC的面积为4cm2,则△BEF的面积等于( )
A.2cm2 B.1cm2 C.0.5 cm2 D.0.25 cm2
3.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=26°,则∠CDE度数为( ).
A.45° B.64° C.71° D.80°.
4.如图,△ABC≌△CDA,若AB=3,BC=4,则四边形ABCD的周长是( )
A.14 B.11 C.16 D.12
5.如图,△ABC≌△ADE,且∠B=25°,∠E=105°,∠DAC=10°,则∠EAC等于( )
A.40° B.50° C.55° D.60°
6.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
7.如图所示,AB、CD相交于点O,△AOC≌△BOD,点E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可能是( )
A.∠OCE=∠ODF B.∠CEA=∠DFB C.CE=DF D.OE=OF
8.等腰三角形的一个角是80°,则它的顶角的度数是( )
A.80° B.80°或20° C.80°或50° D.20°
9.如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线交AC于点E,垂足为D,连接BE,则∠EBC的度数是( )
A.30° B.45° C.60° D.75°
10.如图所示,是等边三角形,且,,则的度数为( )
A. B. C. D.
二、填空题
11.已知一个三角形三边长分别为3,x,5,且x为偶数,则这个三角形的周长为_____.
12.如图,△ABC≌△ADE,其中,点B与D、点C与E是对应点.若∠BAE=120°,∠BAD=40°,则∠BAC的大小为_______.
13.如图,中,,,,,则 ______ 度.
14.如图,在中,,,在上取点,延长到,使得;在上取一点,延长到,使得;…,按此做法进行下去,第n个等腰三角形的底角的度数为__________.
三、解答题
15.如图,已知,在△ABC中,∠C=∠ABC,BE⊥AC,∠DBE=60°,求∠C的度数.
16.如图,在四边形ABCD中,点E是对角线BD上的一点,EA⊥AB,EC⊥BC,且EA=EC.求证:AD=CD.
17.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
18.如图,在△ABC中,AD⊥BC于点D,点F为AB上一点,连接CF,过点B作BE⊥BC交CF的延长线于点E,交AD于点H,且∠1=∠2
(1)求证:AB=AC;
(2)若∠1=22°,∠AFC=110°,求∠BCE的度数.
19.如图,是边长为的等边三角形,是边上一动点,由向运动(与、不重合),是延长线上一动点,与点同时以相同的速度由向延长线方向运动(不与重合),过作于,连接交于.
(1)若时,求的长;
(2)当时,求的长;
(3)在运动过程中线段的长是否发生变化?如果不变,求出线段的长;如果发生变化,请说明理由
答案
1.C
2.B
3.C
4.A
5.D
6.B
7.C
8.B
9.B
10.D
11.12或14
12.80°
13.70
14..
15.∵BE⊥AC,
∴∠AEB=90°,
∵∠DBE=60°,
∴∠A=90°-60°=30°,
∴∠C=∠ABC=(180°-30°)=75°.
16.∵EA⊥AB,EC⊥BC,
∴∠EAB=∠ECB=90°,
在Rt△EAB与Rt△ECB中
,
∴Rt△EAB≌Rt△ECB,
∴AB=CB,∠ABE=∠CBE,
∵BD=BD,
在△ABD与△CBD中
,
∴△ABD≌△CBD,
∴AD=CD.
17.,
,即,
在和中,
,
≌;
≌,
,
,
18.(1)证明:∵EB⊥BC,AD⊥BC,
∴EB∥AD,
∴∠2=∠BAD,
∵∠1=∠2,
∴∠BAD=∠1,
∵∠1+∠ACD=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠ACB,
∴AB=AC.
(2)解:∵∠2=∠1=22°,∠EBC=90°,
∴∠FBC=68°,
∵∠AFC=∠FBC+∠ECB,
∴∠ECB=110°-68°=42°.
19.(1)∵△ABC是等边三角形,
∴∠A=60,
∵PE⊥AB,
∴∠APE=30,
∵AE=1,∠APE=30,PE⊥AB,
∴AP=2AE=2;
(2)解:过P作PF∥QC,
则△AFP是等边三角形,
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30,
∴BD=DF=FA=AB=2,
∴AP=2;
(3)解:由(2)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=BF+FA=AB=3为定值,即DE的长不变
