6.1.1平方根课件(34张ppt)
图片预览











文档简介
(共34张PPT)
6.1.1平方根
1、我们已经学习过哪些运算?它们中互为逆运算的是?
答:加法、减法、乘法、除法、乘方五种运算。
加法与减法互逆;乘法与除法互逆。
2、乘方有没有逆运算?
知识回顾
掌握平方根与算术平方根的概念,能通过开方运算求一个非负数的平方根及算术平方根,理解平方与开平方互为逆运算。
【学习目标】
【学习重点】
【学习难点】
平方根和算术平方根的概念和性质
平方根与算术平方根的区别与联系
新知导入
为了趣味接力比赛,要在运动场上圈出一个面积为100平方米的正方形场地,这个正方形场地的边长为多少?
10米
因为
请你说一说解决问题的思路.
新知讲解
问题1、装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1,如图,问这种地砖一块的边长是多少?
设一块正方形地砖的边长为xm,根据题意,有
怎么求x呢?
新知讲解
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做二次方根.
例如,由于102=100,( -10)2=100,所以100的平方根是+10和-10(可以合写为±10).
新知讲解
1.16的平方根是什么?
2.0的平方根是什么?
3.-9有没有平方根?
交流(课本第2页)
因为,所以16的平方根是
因为,所以0的平方根是
因为不存在一个数的平方等于-9,所以-9没有平方根
让我们一起来表示一个数的平方根
正的平方根用来表示,(读做“根号a”)
即:正数a的平方根表示为±(读做“正、负根号a” )
如:49的平方根表示为 ,
即= ±7
对于正数a
负的平方根用 “-”表示(读做“负根号a” )
其中a叫做被开方数。
新知讲解
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
平方根的性质:
新知讲解
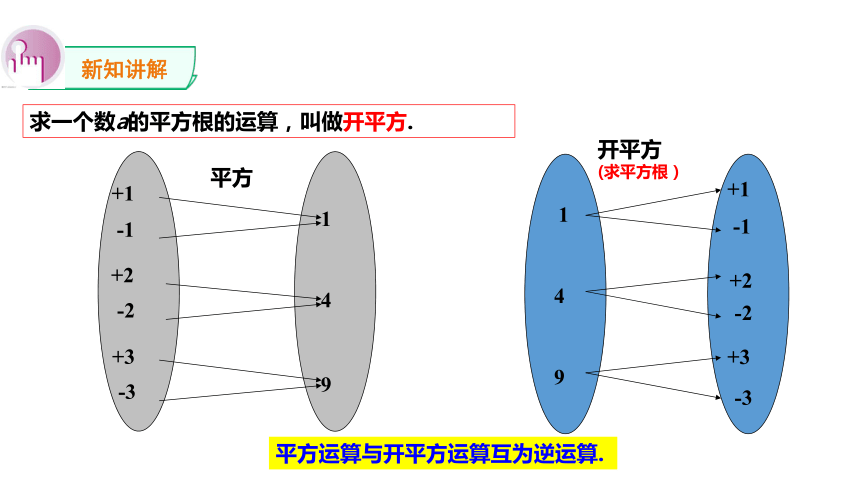
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
(求平方根)
平方
平方运算与开平方运算互为逆运算.
新知讲解
1、我们已经学习过哪些运算?它们中互为逆运算的是?
答:加法、减法、乘法、除法、乘方五种运算。
加法与减法互逆;乘法与除法互逆。
2、乘方有没有逆运算?
解决问题
答:开方。
例题解析
(1) 25 (2) (3) 0.0169 (4) -64
例1 判断下列各数是否有平方根?为什么?
解:因为正数和0都有平方根,负数没有平方根,所以25, ,0.0169都有平方根,-64没有平方根。
考查知识——平方根的性质:
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
正数的平方根有两个,同学们能发现这两个数之间的关系吗?
正数的两个平方根互为相反数,
例:a的一个平方根是5,则另一个平方根是 ,a= .其中______ 是算术平方根.
-5
25
我们把正数的正的平方根叫做算术平方根.
5
新知讲解
一个正数x的平方等于a,即 x2= a,这个正数x叫做a的算术平方根.
a的算术平方根记为,读作“根号a”
x2 = a (x为正数)
规定0的算术平方根是0,记作
也就是说,非负数的“算术”平方根是非负数;负数不存在算术平方根,
即当a<0时,无意义.
新知讲解
新知讲解
例2 求下列各数的平方根和算术平方根。
(1) 1 (2) 81 (3) 64 (4) (-3)2
解:(1) ∵(±1)?=1
(2) ∵(±9)?=81
∴1的平方根是,即,1的算术平方根是1
∴81的平方根是,即,81的算术平方根是±9
新知讲解
(3) ∵(±8)?=64
(4) ∵(-3)?=9
∴64的平方根是,即,64的算术平方根是8
∴9的平方根是,即的平方根是±3,即,的算术平方根是3
平方根与算术平方根的联系与区别
联系:
1.算术平方根是平方根的一种;
2.只有非负数才有算术平方根和平方根;
3.0的算术平方根和平方根都是0.
新知讲解
区别 平方根 算术平方根
定义不同
个数不同
表示法不同
取值范围不同
如果一个数的平方等于a,这个数就叫做a的平方根
正数有两个平方根
非负数a的非负平方根叫a的算术平方根
正数的算术平方根只有一个
正数的平方根一正一负,互为相反数
正数的算术平方根只有一个.
新知讲解
练一练:课本第5页“练习”
1.填空:
(1)一个正数有两个平方根,而且这两个平方根
(2) 有且只有一个平方根,它的平方根就是
(3) 数没有平方根。
互为相反数。
0
0
负
考查知识:平方根的性质:一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根;
2. 判断是非:
(1)4是16的算术平方根。 ( )
(2) 是 的一个平方根。 ( )
(3) 的平方根是-5。 ( )
(4)4是16的算术平方根。 ( )
√
√
√
×
考查知识:平方根和算术平方根的定义。
3.下列各式是否有意义,并说明理由:
(1) (2) (3) (4)
考查知识:只有正数和0有平方根,负数没有平方根。
解:(1)有意义
(2)无意义
(3)有意义
(4)有意义
4.求下列各数的平方根、算术平方根,并用式子
表示。
(1)49 (2)25
解:(1)49的平方根是:
49的算术平方根是:
(2)25的平方根是:
25的算术平方根是:
例3、利用计算器求下列各式的值(精确到0.01)
(1);(2) (3) (4)
解:(1)在计算器上依次键入2=,显示结果
是1.414213562,精确到0.01,得
例题讲解
(2)
(3)-
(4)在计算器上依次键入(5÷7)=,即可得
第二宇宙速度是指使人造卫星脱离地球引力作用范围飞向太阳,并围绕太阳运动所需的最小发射速度
新知讲解
本章引言中提到的速度是第二宇宙速度,,其中g取9.8m/,r取6.4×m,用计算器可求得
(m/s)=11.2(km/s)
例题讲解
例4、如图,跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作.如果不考虑空气阻力等其他因素影响.弹跳到最高点后,人体下落到水面所需要的时间t与下落的高度h之间应遵循下面的公式:
,其中h的单位是m,t的单位是s,g=9.8m/.假设跳板的高度是3m,运动员在跳板上跳起至高出跳板1.2m处开始下落,那么运动员下落到水面约需要多长时间?
解:设运动员下落到水面约需ts,根据题意,得:
3+1.2=
t≈0.93s
例题讲解
1.判断下列说法是否正确:
(1) ±1的平方根是1. ( )
(2) 1的平方根是1. . ( )
(3) -25的平方根是±5. ( )
(4) =±18. ( )
(5) 9是-9 的算术平方根. ( )
(6) -5是25的平方根. ( )
课堂练习
2. 9的算术平方根是( )
A.-3 B.3 C.±3 D.81
3.下列说法正确的是( )
A.任何数都有平方根 B.一个正数的平方根有两个,它们互为倒数
C.只有非负数才有平方根 D.不是正数就没有平方根
课堂练习
B
C
课堂练习
4. 的平方根是_______
5.用计算器计算:≈_______.
6.自由落体公式:(g是重力加速度,它的值约为9.8m/ ),若物体降落的高度S=300m ,用计算器算出降落的时间T = (精确到0.1s )
6.403
7.8s
7. 求下列各数的平方根
(1)100;(2)0;(3);(4)0.09
解:(1)∵所以100的平方根是±10
(2)∵所以0的平方根是0
(3)∵所以的平方根是±
(4)∵所以0.09的平方根是±0.3
课堂练习
一个正数的平方根是2a+3和a-6你能知道a是多少吗?这个正数是几?
拓展提高
解:由平方根的意义知道
(2a+3)+(a-6)=0
得 a=1
这个正数是25.
中考链接
1.(2016. 江苏省秦州市)4的平方根是( )
A.±2 B.-2 C.2 D.±
2.(2018.株洲市)9的算术平方根是( )
A.3 B.9 C.±3 D.±9
A
A
课堂小结
平方根
定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根
性质:
开平方的定义:求一个数的平方根的运算,叫做开平方
1.一个正数有两个平方根,它们互为相反数
2.0的平方根是0
3.负数没有平方根
课堂总结
开平方与平方是互为逆运算。
2.性质:
板书设计
1.定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根
(1)一个正数有两个平方根,它们互为相反数
(2)0的平方根是0
(3)负数没有平方根
3.开平方的定义:
求一个数的平方根的运算,叫做开平方
6.1.1平方根
1、我们已经学习过哪些运算?它们中互为逆运算的是?
答:加法、减法、乘法、除法、乘方五种运算。
加法与减法互逆;乘法与除法互逆。
2、乘方有没有逆运算?
知识回顾
掌握平方根与算术平方根的概念,能通过开方运算求一个非负数的平方根及算术平方根,理解平方与开平方互为逆运算。
【学习目标】
【学习重点】
【学习难点】
平方根和算术平方根的概念和性质
平方根与算术平方根的区别与联系
新知导入
为了趣味接力比赛,要在运动场上圈出一个面积为100平方米的正方形场地,这个正方形场地的边长为多少?
10米
因为
请你说一说解决问题的思路.
新知讲解
问题1、装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1,如图,问这种地砖一块的边长是多少?
设一块正方形地砖的边长为xm,根据题意,有
怎么求x呢?
新知讲解
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做二次方根.
例如,由于102=100,( -10)2=100,所以100的平方根是+10和-10(可以合写为±10).
新知讲解
1.16的平方根是什么?
2.0的平方根是什么?
3.-9有没有平方根?
交流(课本第2页)
因为,所以16的平方根是
因为,所以0的平方根是
因为不存在一个数的平方等于-9,所以-9没有平方根
让我们一起来表示一个数的平方根
正的平方根用来表示,(读做“根号a”)
即:正数a的平方根表示为±(读做“正、负根号a” )
如:49的平方根表示为 ,
即= ±7
对于正数a
负的平方根用 “-”表示(读做“负根号a” )
其中a叫做被开方数。
新知讲解
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
平方根的性质:
新知讲解
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
(求平方根)
平方
平方运算与开平方运算互为逆运算.
新知讲解
1、我们已经学习过哪些运算?它们中互为逆运算的是?
答:加法、减法、乘法、除法、乘方五种运算。
加法与减法互逆;乘法与除法互逆。
2、乘方有没有逆运算?
解决问题
答:开方。
例题解析
(1) 25 (2) (3) 0.0169 (4) -64
例1 判断下列各数是否有平方根?为什么?
解:因为正数和0都有平方根,负数没有平方根,所以25, ,0.0169都有平方根,-64没有平方根。
考查知识——平方根的性质:
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
正数的平方根有两个,同学们能发现这两个数之间的关系吗?
正数的两个平方根互为相反数,
例:a的一个平方根是5,则另一个平方根是 ,a= .其中______ 是算术平方根.
-5
25
我们把正数的正的平方根叫做算术平方根.
5
新知讲解
一个正数x的平方等于a,即 x2= a,这个正数x叫做a的算术平方根.
a的算术平方根记为,读作“根号a”
x2 = a (x为正数)
规定0的算术平方根是0,记作
也就是说,非负数的“算术”平方根是非负数;负数不存在算术平方根,
即当a<0时,无意义.
新知讲解
新知讲解
例2 求下列各数的平方根和算术平方根。
(1) 1 (2) 81 (3) 64 (4) (-3)2
解:(1) ∵(±1)?=1
(2) ∵(±9)?=81
∴1的平方根是,即,1的算术平方根是1
∴81的平方根是,即,81的算术平方根是±9
新知讲解
(3) ∵(±8)?=64
(4) ∵(-3)?=9
∴64的平方根是,即,64的算术平方根是8
∴9的平方根是,即的平方根是±3,即,的算术平方根是3
平方根与算术平方根的联系与区别
联系:
1.算术平方根是平方根的一种;
2.只有非负数才有算术平方根和平方根;
3.0的算术平方根和平方根都是0.
新知讲解
区别 平方根 算术平方根
定义不同
个数不同
表示法不同
取值范围不同
如果一个数的平方等于a,这个数就叫做a的平方根
正数有两个平方根
非负数a的非负平方根叫a的算术平方根
正数的算术平方根只有一个
正数的平方根一正一负,互为相反数
正数的算术平方根只有一个.
新知讲解
练一练:课本第5页“练习”
1.填空:
(1)一个正数有两个平方根,而且这两个平方根
(2) 有且只有一个平方根,它的平方根就是
(3) 数没有平方根。
互为相反数。
0
0
负
考查知识:平方根的性质:一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根;
2. 判断是非:
(1)4是16的算术平方根。 ( )
(2) 是 的一个平方根。 ( )
(3) 的平方根是-5。 ( )
(4)4是16的算术平方根。 ( )
√
√
√
×
考查知识:平方根和算术平方根的定义。
3.下列各式是否有意义,并说明理由:
(1) (2) (3) (4)
考查知识:只有正数和0有平方根,负数没有平方根。
解:(1)有意义
(2)无意义
(3)有意义
(4)有意义
4.求下列各数的平方根、算术平方根,并用式子
表示。
(1)49 (2)25
解:(1)49的平方根是:
49的算术平方根是:
(2)25的平方根是:
25的算术平方根是:
例3、利用计算器求下列各式的值(精确到0.01)
(1);(2) (3) (4)
解:(1)在计算器上依次键入2=,显示结果
是1.414213562,精确到0.01,得
例题讲解
(2)
(3)-
(4)在计算器上依次键入(5÷7)=,即可得
第二宇宙速度是指使人造卫星脱离地球引力作用范围飞向太阳,并围绕太阳运动所需的最小发射速度
新知讲解
本章引言中提到的速度是第二宇宙速度,,其中g取9.8m/,r取6.4×m,用计算器可求得
(m/s)=11.2(km/s)
例题讲解
例4、如图,跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作.如果不考虑空气阻力等其他因素影响.弹跳到最高点后,人体下落到水面所需要的时间t与下落的高度h之间应遵循下面的公式:
,其中h的单位是m,t的单位是s,g=9.8m/.假设跳板的高度是3m,运动员在跳板上跳起至高出跳板1.2m处开始下落,那么运动员下落到水面约需要多长时间?
解:设运动员下落到水面约需ts,根据题意,得:
3+1.2=
t≈0.93s
例题讲解
1.判断下列说法是否正确:
(1) ±1的平方根是1. ( )
(2) 1的平方根是1. . ( )
(3) -25的平方根是±5. ( )
(4) =±18. ( )
(5) 9是-9 的算术平方根. ( )
(6) -5是25的平方根. ( )
课堂练习
2. 9的算术平方根是( )
A.-3 B.3 C.±3 D.81
3.下列说法正确的是( )
A.任何数都有平方根 B.一个正数的平方根有两个,它们互为倒数
C.只有非负数才有平方根 D.不是正数就没有平方根
课堂练习
B
C
课堂练习
4. 的平方根是_______
5.用计算器计算:≈_______.
6.自由落体公式:(g是重力加速度,它的值约为9.8m/ ),若物体降落的高度S=300m ,用计算器算出降落的时间T = (精确到0.1s )
6.403
7.8s
7. 求下列各数的平方根
(1)100;(2)0;(3);(4)0.09
解:(1)∵所以100的平方根是±10
(2)∵所以0的平方根是0
(3)∵所以的平方根是±
(4)∵所以0.09的平方根是±0.3
课堂练习
一个正数的平方根是2a+3和a-6你能知道a是多少吗?这个正数是几?
拓展提高
解:由平方根的意义知道
(2a+3)+(a-6)=0
得 a=1
这个正数是25.
中考链接
1.(2016. 江苏省秦州市)4的平方根是( )
A.±2 B.-2 C.2 D.±
2.(2018.株洲市)9的算术平方根是( )
A.3 B.9 C.±3 D.±9
A
A
课堂小结
平方根
定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根
性质:
开平方的定义:求一个数的平方根的运算,叫做开平方
1.一个正数有两个平方根,它们互为相反数
2.0的平方根是0
3.负数没有平方根
课堂总结
开平方与平方是互为逆运算。
2.性质:
板书设计
1.定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根
(1)一个正数有两个平方根,它们互为相反数
(2)0的平方根是0
(3)负数没有平方根
3.开平方的定义:
求一个数的平方根的运算,叫做开平方
