2020春华师版九下数学:几何的回顾之几何问题的处理方法第1课时课件(31张ppt)
文档属性
| 名称 | 2020春华师版九下数学:几何的回顾之几何问题的处理方法第1课时课件(31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 769.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-25 00:00:00 | ||
图片预览











文档简介
课件31张PPT。第1课时1.探索几何图形属性的两种基本方法是_________和_________.
2.叙述我们学过的8条公理.
答:(1)直线公理:_____确定一条直线;
(2)线段公理:两点之间_____最短;
(3)平行公理:经过已知直线外一点,_________一条直线与已知
直线平行;合情推理逻辑推理两点线段有且只有(4)经过直线外或直线上一点,有且只有一条直线与已知直线
_____;
(5)平行线的判定公理:________相等,两直线平行;
(6)平行线的性质公理:两直线平行, ______相等;
(7)全等三角形的性质公理:全等三角形的_______、_______分
别相等;
(8)全等三角形的判定公理:_________ “A.S.A.”_________.垂直同位角同位角对应边对应角“S.A.S.”“S.S.S.”3.补全以下定理:①三角形的内角和等于_____;②n边形的内
角和等于___________;③三角形的一个外角等于___________
_______________;④直角三角形的两个锐角_____;⑤等腰三
角形的底角_____;⑥等腰三角形_____的平分线、底边上的
_____、底边上的___互相重合;⑦如果一个三角形有两个角相
等,那么这两个角所对的___也相等.180°(n-2)×180°和它不相邻的两个内角的和互余相等顶角中线高边【点拨】公理是人们在长期实践中总结出来的,并把它作为判断
其他命题真假的原始依据.定理可以从公理或其他真命题出发,
用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断
其他命题真假的依据.【预习思考】公理和定理的区别与联系?
提示:(1)公理和定理都是正确的命题.(2)公理和定理的区别主
要在于:公理的正确性是被大家公认的,不需要用推理来证明,
而定理需要证明. 三角形的性质定理
【例1】求直角三角形两锐角平分线相交所成角的度数.
【解题探究】
1.根据题意画出图形:
_________________2.试根据题设、结论,结合图形,写出“已知”和“求解”.
答:已知:在Rt△ABC中,∠ACB=90°,AE,BD分别是∠BAC和
∠ABC的平分线,且AE和BD相交于点O.
求∠AOD和∠EOD的度数.
3.解答:如图,∵AE,BD分别是∠BAC和∠ABC的平分
线,∠ACB=90°.
∴∠OAB+∠OBA=90°÷2=45°,
∴∠AOD=∠OAB+∠OBA=45°,
∴∠EOD=180°-∠AOD=180°-45°=135°.【规律总结】
证明几何命题的三个步骤
1.根据题意画出图形(图形要正确且具有一般性,不能画特殊图
形);
2.根据题设、结论,结合图形,写出“已知”“求证”(或“求
解”);
3.经过分析,找出证明和求解思路(可以从已知向求证探索或从
求证向已知溯源,还可以从已知和求证两个方向同时出发),写出
证明或求解过程(每一步都要有理有据).【跟踪训练】
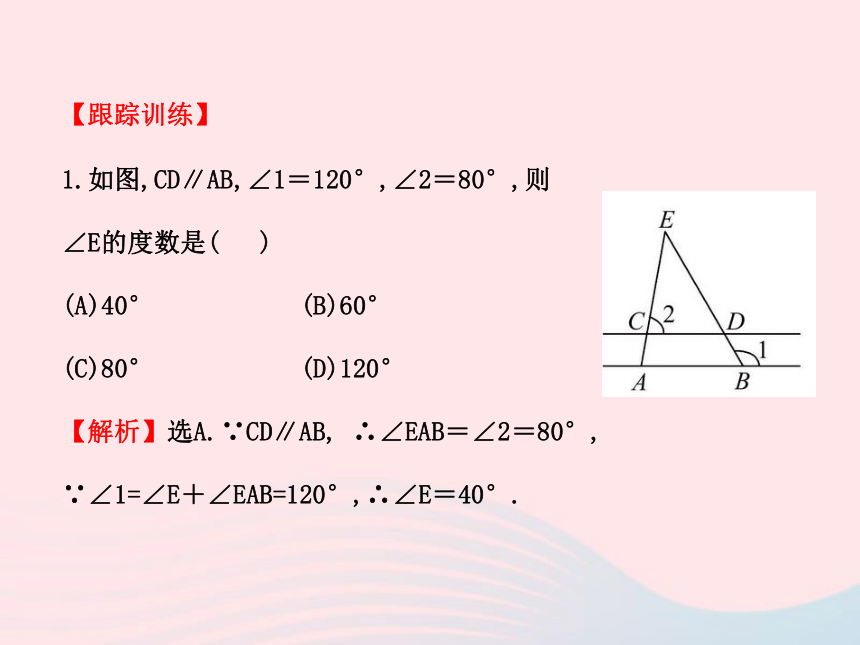
1.如图,CD∥AB,∠1=120°,∠2=80°,则
∠E的度数是( )
(A)40° (B)60°
(C)80° (D)120°
【解析】选A.∵CD∥AB, ∴∠EAB=∠2=80°,
∵∠1=∠E+∠EAB=120°,∴∠E=40°.2.如图,在△ABC中,
D,E分别是AB,AC上的点,点F在BC的延长
线上,DE∥BC,∠A=46°,∠1=52°,则
∠2=_____度.
【解析】∵DE∥BC,∠1=52°.∴∠B=52°.又
∠A=46°,∴∠2=∠A+∠B=98°.
答案:983.如图,在直角△ABC中,
∠C=90°,∠CAB的平分线AD交BC于D,若DE
垂直平分AB,求∠B的度数.
【解析】∵AD平分∠CAB,∴∠CAD=∠BAD.
∵DE垂直平分AB,∴AD=BD,∠B=∠BAD,
∴∠CAD=∠BAD=∠B.
∵在Rt△ABC中,∠C=90°,
∴∠CAD+∠BAD+∠B=90°,∴∠B=30°.【变式训练】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,
垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?【解析】(1)∠PCD=∠PDC.理由如下:
∵OP是∠AOB的平分线,且PC⊥OA,PD⊥OB,
∴PC=PD,∴∠PCD=∠PDC.
(2)OP是CD的垂直平分线.理由如下:在Rt△POC和Rt△POD中,
∵PC=PD,OP=OP,∴Rt△POC≌Rt△POD,
∴OC=OD.由PC=PD,OC=OD,
可知点O,P都是线段CD的垂直平分线上的点,
从而OP是线段CD的垂直平分线. 等腰三角形的性质与判定
【例2】(12分)如图,△ACD和△BCE都是等腰直角三角形,
∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE于点G,H.试猜测
线段AE和BD的关系,并说明理由.
易错提醒:不要忘记线段的关系包括数量关系和位置关系!【规范解答】
猜测 AE=BD,AE⊥BD .………………………………………2分
理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB.………………………………………4分∵△ACD和△BCE都是等腰直角三角形,
∴AC=DC,CE=CB.
∴△ACE≌△DCB(S.A.S.),………………………………………8
∴AE=BD,∠CAE=∠CDB.………………………………………10分
∵∠AFC=∠DFH,∴∠DHF=∠ACD=90°,
∴AE⊥BD.………………………………………12分【互动探究】何为“等腰三角形三线合一”中的“三线”?
提示:“三线”是指底边上的高、底边上的中线及顶角的平分
线.切记不要认为任何一边都具有这种性质.【规律总结】
等腰三角形的判定方法及性质
1.判定等腰三角形的两种方法
(1)等腰三角形的定义;
(2)等腰三角形的判定定理.
2.使用等腰三角形性质的两点注意
(1)要证明的边必须是同一个三角形中的两条边;
(2)在没有证明出是等腰三角形之前不能说“底角”“顶角”
“腰”或“底”等词.【跟踪训练】
4.如图,在△ABC中,AB
=AC,点D,E在BC边上,∠ABD=∠DAE=
∠EAC=36°,则图中共有等腰三角形
的个数是( )
(A)4个 (B)5个 (C)6个 (D)7个
【解析】选C.等腰三角形是△ABC,△ABE,△ABD,△ADE,
△ADC,△AEC.5.如图,△ABC和△ADE
都是等腰直角三角形,∠BAC=∠DAE=90°,
四边形ACDE是平行四边形,连结CE交AD于
点F,连结BD交CE于点G,连结BE.
下列结论中:
①CE=BD; ②△ADC是等腰直角三角形;
③∠ADB=∠AEB; ④CD·AE=EF·CG.
一定正确的结论有( )
(A)1个 (B)2个 (C)3个 (D)4个【解析】选D.根据题意可得△ABD≌△ACE≌△ABE,
△CGD∽△EAF,可知结论①②③④正确,故选D.6.已知:如图,在△ABC中,
D为BC上的一点,AD平分∠EDC,且∠E=∠B,
ED=DC.
求证:AB=AC.
【证明】∵AD平分∠EDC,∴∠ADE=∠ADC,又DE=DC, AD=AD,
∴△ADE≌△ADC,∴∠E=∠C,又∠E=∠B,
∴∠B=∠C,∴AB=AC.1.等腰三角形的顶角为80°,则它的底角
是( )
(A)20° (B)50° (C)60° (D)80°
【解析】选B.底角= =50°.2.如图,△ABC的周长为30 cm,把△ABC的边
AC对折,使顶点C和点A重合,折痕交BC边于
点D,交AC边于点E,连结AD,若AE=4 cm,则
△ABD的周长是( )
(A)22 cm (B)20 cm (C)18 cm (D)15 cm
【解析】选A .∵△ABC的边AC对折,顶点C和点A重合,
∴AE=CE,AE⊥DE,∴AD=CD.△ABD的周长=AB+BD+AD
=AB+BD+CD=AB+BC=△ABC的周长-AC=30-8=22(cm).3.如图,已知a∥b,
小亮把三角板的直角顶点放在直线b上.
若∠1=40°,则∠2的度数为_______.
【解析】如图,∵∠1=40°,
∴∠3=180°-∠1-90°
=180°-40°-90°=50°.
∵a∥b,∴∠2=∠3=50°.
答案:50°4.如图所示,在边长为2的正三角形ABC中,E,F,G分别为AB,AC,
BC的中点,点P是线段EF上一个动点,连结BP,GP,则△BPG周
长的最小值是_______.【解析】要使△BPG的周长最小,而BG=1一定,
只要使BP+PG最短即可.连结AG交EF于M.
∵等边△ABC中,E,F,G分别为AB,
AC,BC的中点,
∴AG⊥BC,EF∥BC,∴AG⊥EF,AM=MG,
∴A,G关于EF对称,
∴P点与E重合时,BP+PG最小,即△BPG的周长最小,最小值
是:PB+PG+BG=AE+BE+BG=AB+BG=2+1=3.
答案:3【高手支招】这类问题可以看作是在定直线的同侧(或异侧)有
两定点,要在定直线上找一点,使得距离最短的一个应用,解决这
个问题的关键在于确定动点的位置.可以巧用轴对称变换,对直
线同侧(或异侧)的两点转化为直线异(或同)侧的两点,根据“两
点之间线段最短”就可以解决.5.如图,△ABC是边
长为3的等边三角形,将△ABC沿直线BC
向右平移,使B点与C点重合,得到△DCE,
连结BD,交AC于F.
(1)猜想AC与BD的位置关系,并证明你的结论 ;
(2)求线段BD的长.【解析】(1)AC⊥BD.
∵△DCE由边长为3的等边△ABC平移而成,
∴AC∥DE,DC=AB=BC=CE,
∴△BDE为直角三角形,
∴∠BDE=90°,∴∠BFC=90°,
∴AC⊥BD.
(2)在Rt△BED中,∵BE=6,DE=3,
∴BD=
2.叙述我们学过的8条公理.
答:(1)直线公理:_____确定一条直线;
(2)线段公理:两点之间_____最短;
(3)平行公理:经过已知直线外一点,_________一条直线与已知
直线平行;合情推理逻辑推理两点线段有且只有(4)经过直线外或直线上一点,有且只有一条直线与已知直线
_____;
(5)平行线的判定公理:________相等,两直线平行;
(6)平行线的性质公理:两直线平行, ______相等;
(7)全等三角形的性质公理:全等三角形的_______、_______分
别相等;
(8)全等三角形的判定公理:_________ “A.S.A.”_________.垂直同位角同位角对应边对应角“S.A.S.”“S.S.S.”3.补全以下定理:①三角形的内角和等于_____;②n边形的内
角和等于___________;③三角形的一个外角等于___________
_______________;④直角三角形的两个锐角_____;⑤等腰三
角形的底角_____;⑥等腰三角形_____的平分线、底边上的
_____、底边上的___互相重合;⑦如果一个三角形有两个角相
等,那么这两个角所对的___也相等.180°(n-2)×180°和它不相邻的两个内角的和互余相等顶角中线高边【点拨】公理是人们在长期实践中总结出来的,并把它作为判断
其他命题真假的原始依据.定理可以从公理或其他真命题出发,
用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断
其他命题真假的依据.【预习思考】公理和定理的区别与联系?
提示:(1)公理和定理都是正确的命题.(2)公理和定理的区别主
要在于:公理的正确性是被大家公认的,不需要用推理来证明,
而定理需要证明. 三角形的性质定理
【例1】求直角三角形两锐角平分线相交所成角的度数.
【解题探究】
1.根据题意画出图形:
_________________2.试根据题设、结论,结合图形,写出“已知”和“求解”.
答:已知:在Rt△ABC中,∠ACB=90°,AE,BD分别是∠BAC和
∠ABC的平分线,且AE和BD相交于点O.
求∠AOD和∠EOD的度数.
3.解答:如图,∵AE,BD分别是∠BAC和∠ABC的平分
线,∠ACB=90°.
∴∠OAB+∠OBA=90°÷2=45°,
∴∠AOD=∠OAB+∠OBA=45°,
∴∠EOD=180°-∠AOD=180°-45°=135°.【规律总结】
证明几何命题的三个步骤
1.根据题意画出图形(图形要正确且具有一般性,不能画特殊图
形);
2.根据题设、结论,结合图形,写出“已知”“求证”(或“求
解”);
3.经过分析,找出证明和求解思路(可以从已知向求证探索或从
求证向已知溯源,还可以从已知和求证两个方向同时出发),写出
证明或求解过程(每一步都要有理有据).【跟踪训练】
1.如图,CD∥AB,∠1=120°,∠2=80°,则
∠E的度数是( )
(A)40° (B)60°
(C)80° (D)120°
【解析】选A.∵CD∥AB, ∴∠EAB=∠2=80°,
∵∠1=∠E+∠EAB=120°,∴∠E=40°.2.如图,在△ABC中,
D,E分别是AB,AC上的点,点F在BC的延长
线上,DE∥BC,∠A=46°,∠1=52°,则
∠2=_____度.
【解析】∵DE∥BC,∠1=52°.∴∠B=52°.又
∠A=46°,∴∠2=∠A+∠B=98°.
答案:983.如图,在直角△ABC中,
∠C=90°,∠CAB的平分线AD交BC于D,若DE
垂直平分AB,求∠B的度数.
【解析】∵AD平分∠CAB,∴∠CAD=∠BAD.
∵DE垂直平分AB,∴AD=BD,∠B=∠BAD,
∴∠CAD=∠BAD=∠B.
∵在Rt△ABC中,∠C=90°,
∴∠CAD+∠BAD+∠B=90°,∴∠B=30°.【变式训练】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,
垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?【解析】(1)∠PCD=∠PDC.理由如下:
∵OP是∠AOB的平分线,且PC⊥OA,PD⊥OB,
∴PC=PD,∴∠PCD=∠PDC.
(2)OP是CD的垂直平分线.理由如下:在Rt△POC和Rt△POD中,
∵PC=PD,OP=OP,∴Rt△POC≌Rt△POD,
∴OC=OD.由PC=PD,OC=OD,
可知点O,P都是线段CD的垂直平分线上的点,
从而OP是线段CD的垂直平分线. 等腰三角形的性质与判定
【例2】(12分)如图,△ACD和△BCE都是等腰直角三角形,
∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE于点G,H.试猜测
线段AE和BD的关系,并说明理由.
易错提醒:不要忘记线段的关系包括数量关系和位置关系!【规范解答】
猜测 AE=BD,AE⊥BD .………………………………………2分
理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB.………………………………………4分∵△ACD和△BCE都是等腰直角三角形,
∴AC=DC,CE=CB.
∴△ACE≌△DCB(S.A.S.),………………………………………8
∴AE=BD,∠CAE=∠CDB.………………………………………10分
∵∠AFC=∠DFH,∴∠DHF=∠ACD=90°,
∴AE⊥BD.………………………………………12分【互动探究】何为“等腰三角形三线合一”中的“三线”?
提示:“三线”是指底边上的高、底边上的中线及顶角的平分
线.切记不要认为任何一边都具有这种性质.【规律总结】
等腰三角形的判定方法及性质
1.判定等腰三角形的两种方法
(1)等腰三角形的定义;
(2)等腰三角形的判定定理.
2.使用等腰三角形性质的两点注意
(1)要证明的边必须是同一个三角形中的两条边;
(2)在没有证明出是等腰三角形之前不能说“底角”“顶角”
“腰”或“底”等词.【跟踪训练】
4.如图,在△ABC中,AB
=AC,点D,E在BC边上,∠ABD=∠DAE=
∠EAC=36°,则图中共有等腰三角形
的个数是( )
(A)4个 (B)5个 (C)6个 (D)7个
【解析】选C.等腰三角形是△ABC,△ABE,△ABD,△ADE,
△ADC,△AEC.5.如图,△ABC和△ADE
都是等腰直角三角形,∠BAC=∠DAE=90°,
四边形ACDE是平行四边形,连结CE交AD于
点F,连结BD交CE于点G,连结BE.
下列结论中:
①CE=BD; ②△ADC是等腰直角三角形;
③∠ADB=∠AEB; ④CD·AE=EF·CG.
一定正确的结论有( )
(A)1个 (B)2个 (C)3个 (D)4个【解析】选D.根据题意可得△ABD≌△ACE≌△ABE,
△CGD∽△EAF,可知结论①②③④正确,故选D.6.已知:如图,在△ABC中,
D为BC上的一点,AD平分∠EDC,且∠E=∠B,
ED=DC.
求证:AB=AC.
【证明】∵AD平分∠EDC,∴∠ADE=∠ADC,又DE=DC, AD=AD,
∴△ADE≌△ADC,∴∠E=∠C,又∠E=∠B,
∴∠B=∠C,∴AB=AC.1.等腰三角形的顶角为80°,则它的底角
是( )
(A)20° (B)50° (C)60° (D)80°
【解析】选B.底角= =50°.2.如图,△ABC的周长为30 cm,把△ABC的边
AC对折,使顶点C和点A重合,折痕交BC边于
点D,交AC边于点E,连结AD,若AE=4 cm,则
△ABD的周长是( )
(A)22 cm (B)20 cm (C)18 cm (D)15 cm
【解析】选A .∵△ABC的边AC对折,顶点C和点A重合,
∴AE=CE,AE⊥DE,∴AD=CD.△ABD的周长=AB+BD+AD
=AB+BD+CD=AB+BC=△ABC的周长-AC=30-8=22(cm).3.如图,已知a∥b,
小亮把三角板的直角顶点放在直线b上.
若∠1=40°,则∠2的度数为_______.
【解析】如图,∵∠1=40°,
∴∠3=180°-∠1-90°
=180°-40°-90°=50°.
∵a∥b,∴∠2=∠3=50°.
答案:50°4.如图所示,在边长为2的正三角形ABC中,E,F,G分别为AB,AC,
BC的中点,点P是线段EF上一个动点,连结BP,GP,则△BPG周
长的最小值是_______.【解析】要使△BPG的周长最小,而BG=1一定,
只要使BP+PG最短即可.连结AG交EF于M.
∵等边△ABC中,E,F,G分别为AB,
AC,BC的中点,
∴AG⊥BC,EF∥BC,∴AG⊥EF,AM=MG,
∴A,G关于EF对称,
∴P点与E重合时,BP+PG最小,即△BPG的周长最小,最小值
是:PB+PG+BG=AE+BE+BG=AB+BG=2+1=3.
答案:3【高手支招】这类问题可以看作是在定直线的同侧(或异侧)有
两定点,要在定直线上找一点,使得距离最短的一个应用,解决这
个问题的关键在于确定动点的位置.可以巧用轴对称变换,对直
线同侧(或异侧)的两点转化为直线异(或同)侧的两点,根据“两
点之间线段最短”就可以解决.5.如图,△ABC是边
长为3的等边三角形,将△ABC沿直线BC
向右平移,使B点与C点重合,得到△DCE,
连结BD,交AC于F.
(1)猜想AC与BD的位置关系,并证明你的结论 ;
(2)求线段BD的长.【解析】(1)AC⊥BD.
∵△DCE由边长为3的等边△ABC平移而成,
∴AC∥DE,DC=AB=BC=CE,
∴△BDE为直角三角形,
∴∠BDE=90°,∴∠BFC=90°,
∴AC⊥BD.
(2)在Rt△BED中,∵BE=6,DE=3,
∴BD=
