北师大版 高中数学 选修2-3 第六章第二节第一课时正态分布的性质及其应用教学课件 (共25张PPT)
文档属性
| 名称 | 北师大版 高中数学 选修2-3 第六章第二节第一课时正态分布的性质及其应用教学课件 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 13:48:04 | ||
图片预览






文档简介
课件25张PPT。2020年4月25日10时46分§2.6 正态分布2020年4月25日10时46分1、掷一枚骰子一次,用X表示所得点数;2、10件产品中有3件次品,从中任取4件,
用X表示取得的次品数;3、抛一枚硬币10次,用X表示正面向上的次数;4、某一自动装置无故障运转的时间X是一个
随机变量,它可以取(0,+∞)内的一切值; 5、某产品的寿命(使用时间)X是一个随机变量,
它可以取[a,b]或[0, +∞)内的一切值;温故而知新2020年4月25日10时46分定义 离散型随机变量:变量X的值可一一列举。
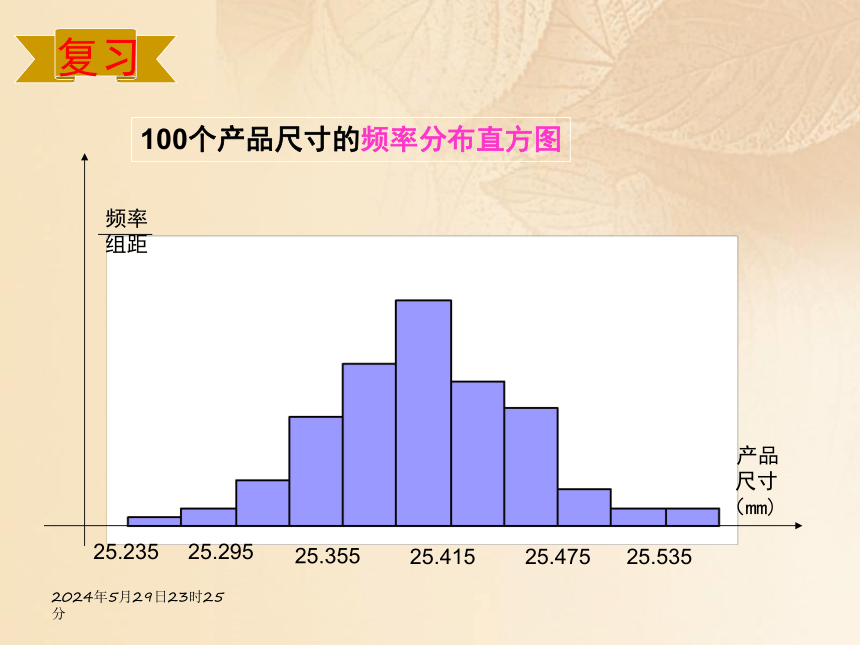
连续型随机变量:变量X的值无法一一列举,它可以在某一个区间内取任意值。2020年4月25日10时46分复习100个产品尺寸的频率分布直方图25.23525.29525.35525.41525.47525.535 产品
尺寸
(mm)频率
组距
2020年4月25日10时46分复习200个产品尺寸的频率分布直方图25.23525.29525.35525.41525.47525.535 产品
尺寸
(mm)频率
组距
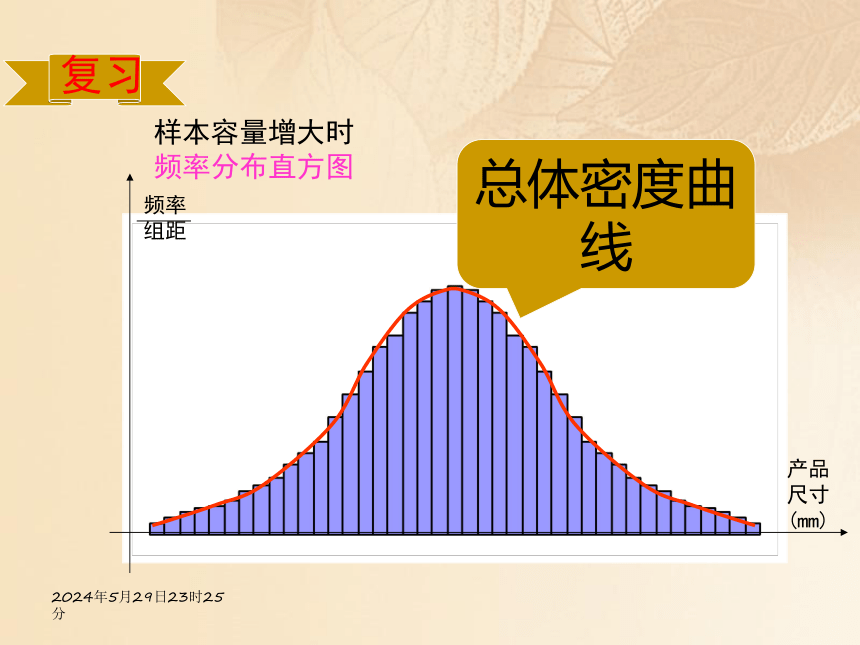
2020年4月25日10时46分复习样本容量增大时
频率分布直方图频率
组距产品
尺寸
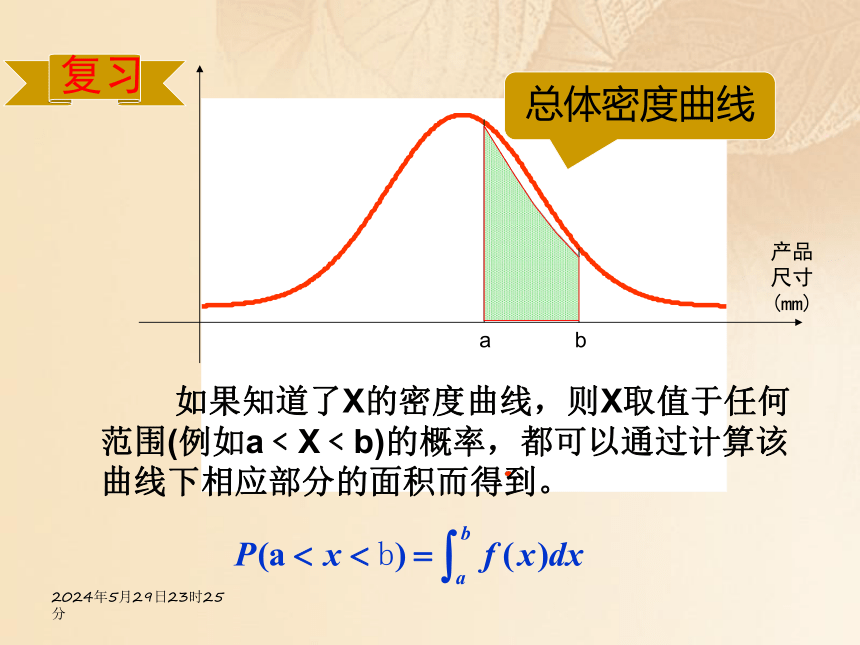
(mm)总体密度曲线2020年4月25日10时46分复习总体密度曲线 如果知道了X的密度曲线,则X取值于任何范围(例如a﹤X﹤b)的概率,都可以通过计算该曲线下相应部分的面积而得到。a b2020年4月25日10时46分导入产品尺寸的总体密度曲线
就是或近似地是以下函数的图象:1 、正态分布的分布密度函数: 式中的实数μ、σ2(σ>0)是参数,分别表示均值与方差,称函数f( x)为正态分布的分布密度函数。2020年4月25日10时46分例1、下列函数是正态密度函数的是( )
A.
B.
C.
D.B2020年4月25日10时46分2、正态分布: 通常用X ~ N( μ,σ2 ) 表示X服从参数为μ和σ2的正态分布。2020年4月25日10时46分3、正态分布图像:2020年4月25日10时46分(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,它关于直线x=μ对称. 4、正态曲线的性质(4)曲线与x轴之间的面积为12020年4月25日10时46分(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近. 4、正态曲线的性质2020年4月25日10时46分5、特殊区间的概率:若X~N ,则对于任何区间(a<x<b)的概率2020年4月25日10时46分例2:2020年4月25日10时46分正态总体的函数表示式当μ= 0,σ=1时2020年4月25日10时46分 在实际遇到的许多随机现象都服从或近似服从正态分布:在生产中,在正常生产条件下各种产品的质量指标; 在测量中,测量结果; 在生物学中,同一群体的某一特征;……; 在气象中,某地每年七月份的平均气温、平均湿度
以及降雨量等,水文中的水位; 总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。2020年4月25日10时46分例3、在某次数学考试中,考生的成绩X服从一个正态分布,即X ~N(90,100).
(1)试求考试成绩X位于区间(70,110)上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?2020年4月25日10时46分1、已知一次考试共有60名同学参加,考生的成绩
X~ (100, 52) ,据此估计,大约应有57人的分数在下
列哪个区间内?( )
(90,110] B. (95,125] C. (100,120] D.(105,115]C练习:2020年4月25日10时46分正态曲线下的面积规律X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。S(-?,-X)S(X,?)=S(-?,-X)?2020年4月25日10时46分正态曲线下的面积规律对称区域面积相等。S(-x2, -x1)-x1 -x2 x2 x1S(x1,x2)=S(-x2,-x1)?2020年4月25日10时46分2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设连续型随机变量X~N(0,1),则 = ,
则 = .
4、若X~N(5,1),求P(6
用X表示取得的次品数;3、抛一枚硬币10次,用X表示正面向上的次数;4、某一自动装置无故障运转的时间X是一个
随机变量,它可以取(0,+∞)内的一切值; 5、某产品的寿命(使用时间)X是一个随机变量,
它可以取[a,b]或[0, +∞)内的一切值;温故而知新2020年4月25日10时46分定义 离散型随机变量:变量X的值可一一列举。
连续型随机变量:变量X的值无法一一列举,它可以在某一个区间内取任意值。2020年4月25日10时46分复习100个产品尺寸的频率分布直方图25.23525.29525.35525.41525.47525.535 产品
尺寸
(mm)频率
组距
2020年4月25日10时46分复习200个产品尺寸的频率分布直方图25.23525.29525.35525.41525.47525.535 产品
尺寸
(mm)频率
组距
2020年4月25日10时46分复习样本容量增大时
频率分布直方图频率
组距产品
尺寸
(mm)总体密度曲线2020年4月25日10时46分复习总体密度曲线 如果知道了X的密度曲线,则X取值于任何范围(例如a﹤X﹤b)的概率,都可以通过计算该曲线下相应部分的面积而得到。a b2020年4月25日10时46分导入产品尺寸的总体密度曲线
就是或近似地是以下函数的图象:1 、正态分布的分布密度函数: 式中的实数μ、σ2(σ>0)是参数,分别表示均值与方差,称函数f( x)为正态分布的分布密度函数。2020年4月25日10时46分例1、下列函数是正态密度函数的是( )
A.
B.
C.
D.B2020年4月25日10时46分2、正态分布: 通常用X ~ N( μ,σ2 ) 表示X服从参数为μ和σ2的正态分布。2020年4月25日10时46分3、正态分布图像:2020年4月25日10时46分(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,它关于直线x=μ对称. 4、正态曲线的性质(4)曲线与x轴之间的面积为12020年4月25日10时46分(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近. 4、正态曲线的性质2020年4月25日10时46分5、特殊区间的概率:若X~N ,则对于任何区间(a<x<b)的概率2020年4月25日10时46分例2:2020年4月25日10时46分正态总体的函数表示式当μ= 0,σ=1时2020年4月25日10时46分 在实际遇到的许多随机现象都服从或近似服从正态分布:在生产中,在正常生产条件下各种产品的质量指标; 在测量中,测量结果; 在生物学中,同一群体的某一特征;……; 在气象中,某地每年七月份的平均气温、平均湿度
以及降雨量等,水文中的水位; 总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。2020年4月25日10时46分例3、在某次数学考试中,考生的成绩X服从一个正态分布,即X ~N(90,100).
(1)试求考试成绩X位于区间(70,110)上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?2020年4月25日10时46分1、已知一次考试共有60名同学参加,考生的成绩
X~ (100, 52) ,据此估计,大约应有57人的分数在下
列哪个区间内?( )
(90,110] B. (95,125] C. (100,120] D.(105,115]C练习:2020年4月25日10时46分正态曲线下的面积规律X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。S(-?,-X)S(X,?)=S(-?,-X)?2020年4月25日10时46分正态曲线下的面积规律对称区域面积相等。S(-x2, -x1)-x1 -x2 x2 x1S(x1,x2)=S(-x2,-x1)?2020年4月25日10时46分2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设连续型随机变量X~N(0,1),则 = ,
则 = .
4、若X~N(5,1),求P(6
同课章节目录
