2020中考数学专题2——几何模型之“K”型相似学案(含解析)
文档属性
| 名称 | 2020中考数学专题2——几何模型之“K”型相似学案(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 16:09:48 | ||
图片预览




文档简介
(
1
)
【模型解析】
2020 中考专题 2——几何模型之“K”型相似
班级 姓名 .
D
A
(
条件:
B
,
C
,
E
三点共线
,
∠
B
=
∠
A
C
D=
∠
E
=
9
0
°
结论:
△
ABC
∽△
CED
) (
条件:
B
,
D
,
C
三点共线
,
∠
B=
∠
EDF=
∠
C=
α
结论
:△
BDE
∽△
CFD
)B C E
【例题分析】
例 1. (1)问题:如图 1,在四边形 ABCD 中,点 P 为 AB 上一点,∠DPC=∠A=∠B=90°,求证:
AD﹒BC=AP﹒BP;
探究:如图 2,在四边形 ABCD 中,点 P 为 AB 上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
应用:请利用(1)(2)获得的经验解决问题:
如图 3,在△ABD 中,AB=6,AD=BD=5,点 P 以每秒 1 个单位长度的速度,由点 A 出发,沿边
AB 向点 B 运动,且满足∠CPD=∠A,设点 P 的运动时间为 t(秒),当 DC=4BC 时,求 t 的值.
例 2.如图,在等边△ABC 中,将△ABC 沿着 MN 折叠。使点 A 落在边 BC 上的点 D 处。(1)若 AB=4,当△BMD 为直角三角形时,求 AM 的长。
(2)当 BD:CD=1:3 时,求 AM:AN 的值。
例 3.如图,在直角坐标系中,矩形 ABCO 的边 OA 在 x 轴上,边 OC 在 y 轴上,点 B 的坐标为(4,8), 将矩形沿对角线 AC 翻折,B 点落在 D 点的位置,且 AD 交 y 轴于点 E,那么点 D 的坐标为 .
例 3 图 例 4 图 例 5 图
例 4.如图,矩形 ABCD 中,AB=2AD,点 A(0,1),点 C、D 在反比例函数 y ? k (k ? 0) 的图象上,
x
AB 与 x 轴的正半轴相交于点 E,若 E 为 AB 的中点,则 k 的值为 .
例 5.如图,直线 a∥b∥c,a 与 b 之间的距离为 3,b 与 c 之间的距离为 6,a、b、c 分别经过等边三角形 ABC 的三个顶点,则三角形的边长为 .
【巩固训练】
如图 1,已知△ABC 和△ADE 均为等边三角形,D 在 BC 上,DE 与 AC 相交于点 F,AB=9,BD=
3,则 CF 等于( )
A.1 B.2 C.3 D.4
图 1 图 2 图 3 图 4
(
3
)如图 2 坐标系中,O(0,0),A(6,6 ),B(12,0),将△OAB 沿直线线 CD 折叠,使点 A 恰
好落在线段 OB 上的点 E 处,若 OE= 24 ,则 CE:DE 的值是 .
5
如图3,直线l1∥l2∥l3,等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,
AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则△ABC的面积为 .
5 k
如图 4,边长为 的正方形 ABCD 的顶点 A 在 y 轴上,顶点 D 在反比例函数 y= (x>0)的图象上,
4 x
已知点 B 的坐标是 3, 9 ,则 k 的值为 。
4 4
如图 5,在平面直角坐标系中,点 A、C 分别在 x 轴、y 轴上,四边形 ABCO 为矩形,AB=16,
4
点 D 与点 A 关于 y 轴对称,tan∠ACB=
3
,∠CDE=∠CAO,点 E、F 分别是线段 AD、AC 上的动
点(点 E 不与点 A、D 重合),且∠CEF=∠ACB.
求 AC 的长和点 D 的坐标;
证明:△AEF∽△DCE;
当△EFC 为等腰三角形时,求点 E 的坐标.
图 5
如图 6,一条抛物线经过原点和点 C(8,0),A、B 是该抛物线上的两点,AB∥x 轴,OA=5,AB=2.点 E 在线段 OC 上,作∠MEN=∠AOC,使∠MEN 的一边始终经过点 A,另一边交线段 BC 于点 F,连接 AF.
求抛物线的解析式;
当点 F 是 BC 的中点时,求点 E 的坐标;
当△AEF 是等腰三角形时,求点 E 的坐标.
图 6
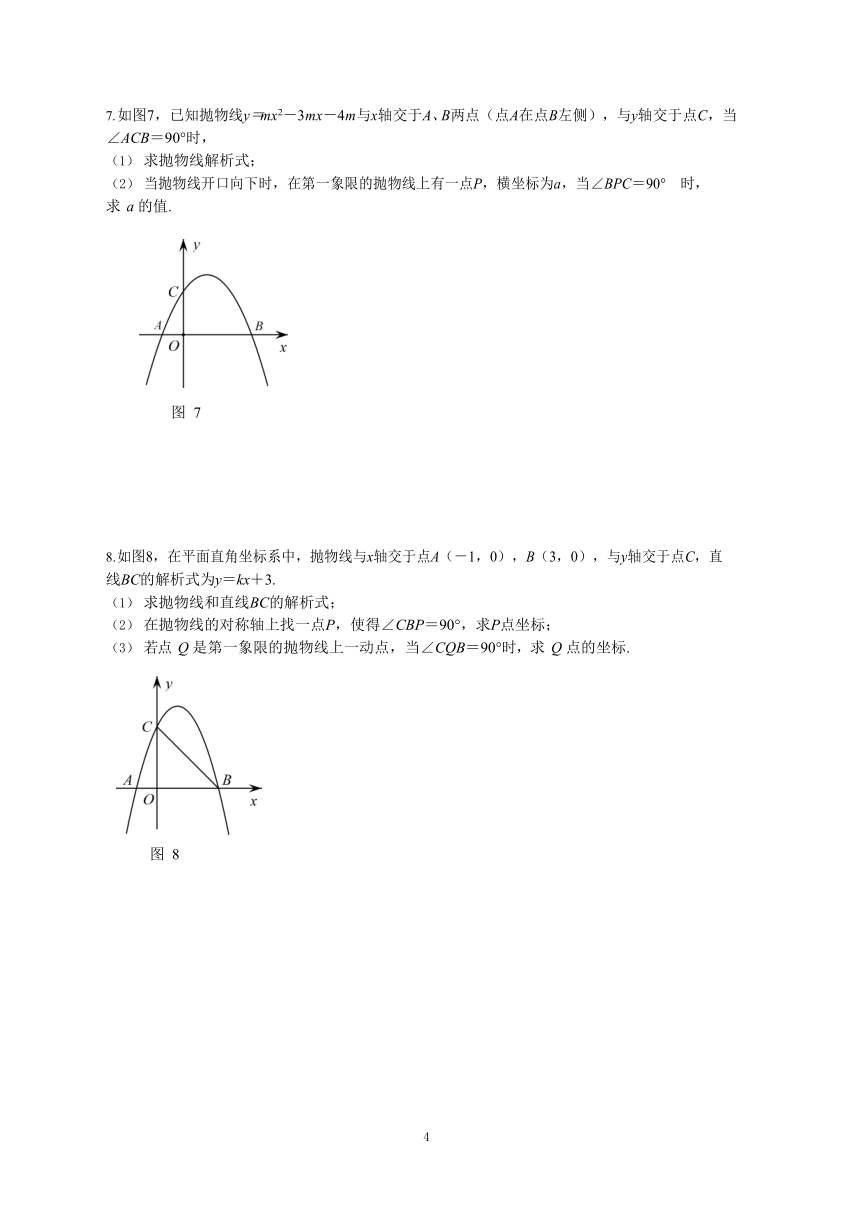
如图7,已知抛物线y=mx2-3mx-4m与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,当
∠ACB=90°时,
求抛物线解析式;
当抛物线开口向下时,在第一象限的抛物线上有一点P,横坐标为a,当∠BPC=90° 时,求 a 的值.
图 7
如图8,在平面直角坐标系中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C,直 线BC的解析式为y=kx+3.
求抛物线和直线BC的解析式;
在抛物线的对称轴上找一点P,使得∠CBP=90°,求P点坐标;
若点 Q 是第一象限的抛物线上一动点,当∠CQB=90°时,求 Q 点的坐标.
图 8
小明是一个喜欢探究钻研的学生,他在和同学们一起研究某条抛物线 y=ax2(a<0)的性质时, 将一把直角三角板的直角顶点置于平面直角坐标系的原点 O,两直角边与该抛物线交于 A、B 两点,请解答以下问题:
图 1 图 2
(
2
)小明测得 OA=OB= 4 (如图 1),求 a 的值;
对同一条抛物线,小明将三角板绕点 O 旋转到如图 2 所示位置时,过 B 作 BF⊥x 轴于点F,测得 OF=2,写出此时点 B 的坐标,并求点 A 的横坐标;
对该抛物线,小明将三角板绕点 O 旋转任意角度时惊奇地发现,交点 A、B 的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
2020 中考专题 2——几何模型之“K”型相似 参考答案
例 1.解:(1)如图 1,
∵∠DPC=∠A=∠B=90°,∴∠ADP+∠APD=90°,∠BPC+∠APD=90°,
∴∠ADP=∠BPC,∴△ADP∽△BPC,
∴ = ,∴AD?BC=AP?BP;
图 1 图 2 图 3
结论 AD?BC=AP?BP 仍然成立. 理由:如图 2,
∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP.
∵∠DPC=∠A=∠B=θ,∴∠BPC=∠ADP,
∴△ADP∽△BPC,∴ = ,∴AD?BC=AP?BP;
如图 3,
∵DC=4BC,又∵AD=BD=5,∴DC=4,BC=1,
,由(1)、(2)的经验可知 AD?BC=AP?BP,
∴5×1=t(6﹣t),解得:t1=1,t2=5,∴t 的值为 1 秒或 5 秒.
例 2.解:(1)如图 1,设 BM=k,AM=DM= 3k.可得方程 k+ 3k=4,得 k=2+2 3,得 AM=2(3
(
-
3
)
.
)
同理,如图 2,可求得 AM=8 3-12.
如图 3,设 BD=m,CD=3m,可得△BDM 与△CDN 的周长比即相似比为 5:7.可得 AM:AN= DM:DN=5:7.
图 1 图 2 图 3
例 3.解:如图,过 D 作 DF⊥x 轴于 F,
∵点 B 的坐标为(4,8),∴AO=4,AB=8,
根据折叠可知:CD=OA,而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,∴OE=DE,OA=CD=4, 设 OE=x,那么 CE=8﹣x,DE=x,
∴在 Rt△DCE 中,CE2=DE2+CD2,
∴(8﹣x)2=x2+42,∴x=3,
又 DF⊥AF,∴DF∥EO,∴△AEO∽△ADF, 而 AD=AB=8,∴AE=CE=8﹣3=5,
∴ = = ,即 ,
∴DF= ,AF= ,∴OF= ﹣4= ,
∴D 的坐标为(﹣,).故答案是:(﹣,).
例 4.解:如图,作 DF⊥y 轴于 F,过 B 点作 x 轴的平行线与过 C 点垂直与 x 轴的直线交于 G, CG 交 x 轴于 K,作 BH⊥x 轴于 H,
∵四边形 ABCD 是矩形,∴∠BAD=90°,
∴∠DAF+∠OAE=90°,
∵∠AEO+∠OAE=90°,∴∠DAF=∠AEO,
∵AB=2AD,E 为 AB 的中点,∴AD=AE, 在△ADF 和△EAO 中,
∴△ADF≌△EAO(AAS),
∴DF=OA=1,AF=OE,∴D(1,k),
∴AF=k﹣1,
同理;△AOE≌△BHE,△ADF≌△CBG,
∴BH=BG=DF=OA=1,EH=CG=OE=AF=k﹣1,
∴OK=2(k﹣1)+1=2k﹣1,CK=k﹣2
∴C(2k﹣1,k﹣2),
∴(2k﹣1)(k﹣2)=1?k, 解得 k1=,k2= ,
∵k﹣1>0,∴k= 故答案是: .
例 5.简解:构造∠BDC=∠AEC=60°,可得△BCD≌△CAE.可求得 AC=2 21.
【巩固训练】
解:如图,∵△ABC 和△ADE 均为等边三角形,
∴∠B=∠BAC=60°,
∴∠BAD+∠ADB=120°,∠ADB+∠FDC=120°
∴∠BAD=∠FDC
又∵∠B=∠C=60°,∴△ABD~△CDF,
∴AB:BD=CD:CF,即 9:3=(9﹣3):CF,∴CF=2.
解:过 A 作 AF⊥OB 于 F,
∵A(6,6),B(12,0),∴AF=6,OF=6,OB=12,
∴BF=6,∴OF=BF,∴AO=AB,
∵tan∠AOB= ,∴∠AOB=60°,∴△AOB 是等边三角形,
∴∠AOB=∠ABO=60°,
∵将△OAB 沿直线线 CD 折叠,使点 A 恰好落在线段 OB 上的点 E 处,
∴∠CED=∠OAB=60°,∴∠OCE=∠DEB,∴△CEO∽△DBE,
∴ ,
设 CE=a,则 CA=a,CO=12﹣a,ED=b,则 AD=b,DB=12﹣b,
,∴24b=60a﹣5ab①, ,
∴36a=60b﹣5ab②,
②﹣①得:36a﹣24b=60b﹣60a,
∴ = ,即 CE:DE= .故答案为: .
简解:构造一对直角三角形全等,可得 BC=AC=5.
解:如图,作 DE⊥OA 于 E,BF⊥OA 于 F,
∵四边形 ABCD 是正方形,
∴AD=AB,∠DAB=90°,
∵∠EAD+∠FAB=90°,∠FAB+∠ABF=90°,
∴∠EAD=∠ABF, 在△ADE 和△BAF 中,
,∴△ADE≌△BAF,
∴AF=ED,AE=BF,
∵B 点坐标(,),AB=,
∴OF= ,AF=DE= = =1.
∴OE=4,点 D 坐标(1,4),∴k=4.
解:(1)由题意 tan∠ACB=,∴cos∠ACB=,
∵四边形 ABCO 为矩形,AB=16,
∴BC= =12,AC= =20,
∴A(﹣12,0),
∵点 D 与点 A 关于 y 轴对称,∴D(12,0);
∵点 D 与点 A 关于 y 轴对称,
∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE,
∴∠AEF=∠DCE,
∴△AEF∽△DCE;
当△EFC 为等腰三角形时,有以下三种情况:
①当 CE=EF 时,
∵△AEF∽△DCE,
∴△AEF≌△DCE,
∴AE=CD=20,
∴OE=AE﹣OA=20﹣12=8,
∴E(8,0);
②当 EF=FC 时,过点 F 作 FM⊥CE 于 M,则点 M 为 CE 中点,
∴CE=2ME=2EF?cos∠CEF=2EF?cos∠ACB= EF,
∵△AEF∽△DCE,
∴ = ,即 = ,
∴AE= ,
∴DE=AE﹣OA= ﹣12=,
∴E(,0);
③当 CE=CF 时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=CAO,即此时点 E 与点 D 重合,这与已知条件矛盾, 综上所述,E(8,0)或(,0).
6.解:(1)如图,
∵该抛物线经过原点和点 C(8,0),
∴设该抛物线的解析式为:y=ax(x﹣8)(a≠0).
∵点 C(8,0),∴该抛物线的对称轴是 x=4.
∵AB=2,AB∥x 轴,∴设 A(3,t),B(5,t),又∵OA=5,∴t=4,即 A(3,4),B(5,4),
∴把点 A 的坐标代入解析式,得
4=3a×(3﹣8),解得 a=﹣ ,
∴该抛物线的解析式是:y=﹣x(x﹣8)(或 y=﹣x2+x);
∵AB∥x 轴,
∴根据抛物线的对称性知 OA=CB=5,∠AOC=∠BCO,
∵点 F 是 BC 的中点,∴CF=.
∵∠MEN=∠AOC,即∠AEF=∠AOC,∠AEC=∠AEF+∠CEF=∠AOC+∠OAE,
∴∠CEF=∠OAE,∴△AOE∽△ECF,
∴ = ,即 = ,
解得,OE= ,或 OE= ,则 E( ,0);
①当 AE=EF 时,可证△AOE≌△ECF. 则 OA=CE=5,∴OE=3,则 E(3,0);
②当 AF=EF 时,过点 F 作 FK∥AO.
易证△ABF≌△FKE,求得 OE=,则 E(,0);
③当 AE=AF 时,在 AO 上取点 Q,使得 EQ=OE. 易证△ABF≌△EQA,则 EQ=AB=2,
∴OE=2.则 E(2,0);
综上所述,点 E 的坐标是:(3,0)、(,0)或(2,0)时,△AEF 是等腰三角形.
6.解:(1)A(-1,0),B(4,0),C(0,-4m).利用 AO?BO
=CO2 列方程可得 m=-1
2
(2) 构 造 基 本 图 形 , 设 P ( a,b ) , 其 中
b=-1 2
,NP=4-a.
(a -3a-4),CM=b-2,BN=b,PN=4-a
2
可得方程 a(4-a)=b(b-2)即,
a(4-a)=
解:
1
- (a-4)(a+1)(
2
1a2+
(
-
)2
3
a),
2
得 a=3(-1,0,3 舍去)
(1)C(0,3),抛物线为 y=-(x+1)(x-3)=-x2+2x+3.
直线 BC 为 y=-x+3,取 BC 的中点 M
3,3)MP=1/2BC=3/2 2, 得 P 3,3 3 2)
(
(
) (
(
) (
±
)2 2 2 2 2
(
1
+
5 5
+
5
2
,
2
)设 Q(a,b)则类似第 6 题,可得 Q
解:(1)设线段 AB 与 y 轴的交点为 C,由抛物线的对称性可得 C 为 AB 中点,
∵OA=OB=4 ,∠AOB=90°,∴AC=OC=BC=4,
∴B(4,﹣4),
将 B(4,﹣4)代入抛物线 y=ax2(a<0)得,a=﹣.
(2)过点 A 作 AE⊥x 轴于点 E,
∵点 B 的横坐标为 2,∴B (2,﹣1),设 A(﹣m,﹣m 2)(m>0),则
OB2=22+12=5,OA2=m2+ m4,AB2=(2+m)2+(﹣1+ m2)2,
∵∠AOB=90°,∴AB2=OA2+OB2,
∴(2+m)2+(﹣1+ m2)2=m2+ m4+5,
解得:m=0(不合题意舍去)或 m=8,即点 A 的横坐标为﹣8.
(3)设 A(﹣m,﹣m 2)(m>0),B(n,﹣n 2)(n>0),设直线 AB 的解析式为:y=kx+b,则 ,
①×n+②×m 得,(m+n)b=﹣(m2n+mn2)=﹣mn(m+n),
∴b=﹣ mn,
由前可知,OB2=n2+ n4,OA2=m2+ m4,AB2=(n+m)2+(﹣ m2+ n2)2, 由 AB2=OA2+OB2,得:n2+n4+m2+ m4=(n+m)2+(﹣ m2+ n2)2,
化简,得 mn=16.
∴b=﹣ ×16=﹣4.由此可知不论 k 为何值,直线 AB 恒过点(0,﹣4).
同课章节目录
