2020年浙江省科学中考专题复习——浮力培优题(有解析)
文档属性
| 名称 | 2020年浙江省科学中考专题复习——浮力培优题(有解析) |  | |
| 格式 | zip | ||
| 文件大小 | 492.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2020-04-24 19:01:32 | ||
图片预览




文档简介
中考科学专题复习——浮力培优题
选择题
1. 如图1,在一个较大的容器中盛有水,水中放有一个木块,木块上面放有铁块A,此时木块漂浮;如果将A从木块上拿下后悬挂在木块下面如图2,并放入水中,当木块和A都静止时(水未溢出),下面说法正确的是( ) A. 容器中水面上升 B. 容器中水面下降 C. 容器中水面不变 D. 无法判断
2. 盛有液体的圆柱形容器置于水平桌面上,如图甲所示,容器对桌面的压强为500Pa;用细线拴一金属球,将金属球浸没在液体中,如图乙所示,容器对桌面的压强为600Pa;将细线剪断,金属球沉到容器底部,如图丙所示,容器对桌面的压强为1500Pa。已知:容器的底面积为100cm2,金属球的密度为8g/cm3,g取10N/kg。则下列判断正确的是( ) A. 金属球所受浮力是6N B. 金属球的体积是100cm3 C. 液体的密度是0.8g/cm3 D. 金属球对容器底部的压力是10N
3. 圆柱形容器中装有适量的水,将一只装有配重的薄壁长烧杯放入圆柱形容器的水中,烧杯静止时容器中水的深度H 1为20cm,如图甲所示.将金属块A吊在烧杯底部,烧杯静止时露出水面的高度h 1为5cm,容器中水的深度H 2为35cm,如图乙所示.将金属块A放在烧杯中,烧杯静止时露出水面的高度h 2为1cm,如图丙所示.已知圆柱形容器底面积为烧杯底面积的2倍.则金属块A的密度为 kg/m 3.
4. 底面积为100cm2的烧杯中装有适量水.当金属块浸没在水中静止时,如图甲所示,弹簧测力计的示数F1=3.4N,水对杯底的压强为p1;当金属块总体积的1/4露出水面静止时,如图乙所示,弹簧测力计的示数为F2,水对杯底的压强为p2;若p1、p2之差为50Pa,g取10N/kg,则( ) A. 金属块的体积V金是2×10-3m3 B. 弹簧测力计的示数F2是5.4N C. 金属块的密度是2.7×103kg/m3 D. 金属块受到的重力是6.8N
5. 如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体A浸没在水中,细绳对物体的拉力为F拉.如图乙所示,当物体A有的体积露出水面时,作用在物体A上的竖直向上的拉力为4N,筒中水的深度比图甲中水的深度下降了0.4cm,此时,物体A所受的浮力为F浮,水在物体A底面处产生的压强为p.g取10N/kg,悬挂物体的细绳的质量忽略不计.( ) A. F拉的大小为4.8N B. F浮的大小为0.2N C. ρA的大小为8g/cm3 D. p的大小为300Pa
6. 如图甲所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h,试管壁粗细均匀,厚度不计;现将一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好仍为h,如图乙所示,若试管横截面积与容器横截面积之比为1:5,则下列说法正确的是( ) A. 放入的物块密度为5×10 3kg/m 3 B. 放入的物块密度为1.25×10 3kg/m 3 C. 放入的物块密度为2.25×10 3kg/m 3 D. 小试管与容器内水面变化的高度相等
7.把一根蜡烛放入盛满酒精的容器中,溢出酒精的质量为4克,若把蜡烛放入盛满水的容器中,则溢出水的质量为(蜡烛的密度为0.9克/立方厘米)( ) A. 4克 B. 5克 C. 4.5克 D. 3.6克
8. 将一实心物体先后投入足量的水和酒精中,物体静止时,所受浮力分别为和,判定物体在水酒精中的浮沉状态可能是( ) A、在水中漂浮,在酒精中漂浮 B、在水中漂浮,在酒精中沉底 C、在水中悬浮,在酒精中漂浮 D、在水中沉底,在酒精中沉底
9. 如将一只盛有水的薄塑料袋,用细线扎紧袋口,用弹簧测力计测得其重力为9N,再将这个装水的塑料袋浸入水中,当弹簧测力计示数为7N时,袋内水面与袋外水面相比较( ) A. 塑料袋内水面比袋外水面高 B. 塑料袋内水面比袋外水面低 C. 塑料袋内水面与袋外水面相平 D. 塑料袋内水面与袋外水面高低无法判断
10. 如图,厕所里自动冲洗的水箱里有一个圆柱形的浮筒P,下水管口有一塞子a,两者用短链相连,若水箱的深度足够,要实现自动定时冲洗,则( ) A. 只要浮筒P的体积足够大 B. 浮筒P的截面必须大于塞子a的截面 C. 只要浮筒P足够轻 D. 浮筒P的截面必须小于塞子a的截面
11. 如图所示,柱形容器的底面积为200cm2,边长为10cm的正方体实心冰块悬浮在油水分层液体中,冰会逐渐熔化,已知浸在分层液体中的物体受到的浮力大小等于它排开所有液体的总重力,ρ油=0.75×103kg/m3,ρ冰=0.9×103kg/m3,下列选项正确的是( ) A. 最初冰块浸在油中的体积是600cm3 B. 冰块完全熔化后,油面下降了0.5cm C. 冰块完全熔化后水对容器底的压强增加了150Pa D. 冰块完全熔化前,逐渐变小的冰块浸在油中的比例逐渐变大
12. 甲溢水杯盛满密度为ρ1的液体,乙溢水杯盛满密度为ρ2的液体.将密度为ρA的小球A轻轻放入甲溢水杯,小球漂浮且有 体积露出液面,甲溢水杯溢出液体的质量是36g.将密度为ρB的小球B轻轻放入乙溢水杯,小球浸没在液体中,并下沉,乙溢水杯溢出液体的质量是30g.已知小球A与小球B体积之比是1:2(g取10N/kg).则下列选项中正确的是( ) A. 小球A的质量为7.2g B. 小球B的质量为30g C. ρ1与ρ2之比为3:1 D. ρA与ρB之比为12:5
13. 4 个边长均为 L 的相同的立方体木块,用胶水(胶水质量不计)粘在一起放入水中,露 出水面的高度为 L/2,如图所示。当胶水溶于水后,木块散开,这时(? )
A. a、b 露出水面高度为 L/2,c、d 为零 B. a、b 露出水面高度为 L/2,c、d 沉入水底 C. a、b、c、d 露出水面高度都是 L/2 D. a、b、c、d 露出水面高度都是 L/4
14.已知A、C均为实心铁块(ρ铁=7.9g/cm3),B为不吸水木块,将A放在B上,B刚好浸没在水中,如图甲;取出A,并将C用轻质细线悬挂在B的底部(C未与容器底部接触,不计操作时带出的水),也能使B刚好浸没,如图乙;柱形容器足够高,且容器底面积是B底面积的三倍,则下列说法中正确的是( ) A. 甲乙两图中,水对容器底部的压强相等
B. A、C两物体的体积之比为69:79 C. 乙图中,剪断BC之间的绳子,水对容器底部压力的变化量等于容器对桌面压力的变化量 D. 乙图中,剪断BC之间的绳子,水面静止时,B相对于容器底部上升的高度等于水面下降的高度
15.一种液体的密度随深度而增大,它的变化规律是ρ1=ρ+kh,式中ρ、k是常数,h表示深度.设深度足够,有一个密度为ρ′的实心小球投入此液体中,且ρ′>ρ,则正确的判断是( ) A. 小球将一沉到底,不再运动 B. 小球将漂浮在液面,不能下沉 C. 小球经过一段运动过程,最终悬浮在深处 D. 小球经过一段运动过程,最终悬浮在深处
如图所示,一块0℃的冰放在盛有0℃的水的容器中.已知冰块与容器底部相接触并相互间有压力,则当冰完全融化为0℃的水后.容器中水面的位置将( ) A. 上升 B. 下降 C. 保持不变 D. 水面的升或降决定于冰和容器内水的体积
填空题
17.在水平桌面上竖直放置一个底面积为S的圆柱形容器,内装密度为 液体,将挂在弹簧秤上体积为V的实心金属球浸没在该液体中(液体未溢出),物体静止时,弹簧秤示数为F;撤去弹簧秤,球下沉并静止于容器底部,此时液体对容器底部的压力为容器底对金属球的支持力的n倍。
求: (1)金属球的密度 ??????????????????????; (2)圆柱形容器内液体的质量 ????????????????。
18.如图所示,边长为L的正方体空心金属盒和实心金属球各一个.若把球放在盒内密封后,放入密度为ρ的液体中金属盒有h 1的高度露出液面,如图甲所示;若把球和盒用细绳相连放入液体中静止后,金属盒有h 2的高度露出液面,如图乙所示;若把球和盒分别放入液体中静止后,金属盒有h 3的高度露出液面,金属球沉入液体底部,如图丙所示.不计细线的重力和体积.金属球的密度ρ球= .
19.如图所示,质量为540g的凹形铝槽,放入底面积为100cm2的圆柱形液体中,铝槽浮在液面上,槽口恰好与液面相平,这时液面上升了2.7cm,若使铝槽沉入液体中,则沉入前后液体对容器底部的压强变化△P= Pa.(已知ρ铝=2.7×103kg/m3;g=10N/kg)
20. 如图甲所示;一个底面积为50cm2的烧杯装有某种液体,把小石块放在木块上,静止时液体深h1=16cm;如图乙所示;若将小石块放入液体中,液体深h2=12cm,石块对杯底的压力F=1.6N;如图丙所示,取出小石块后,液体深h3=10cm.则小石块的密度ρ石为????kg/m3.(g取10N/kg)
21. 小阳想测出一块鹅卵石的密度.他在家中利用刻度尺、口大底小的塑料碗、大烧杯和适量的水进行实验,在烧杯内放入适量水,再将塑料碗轻轻放入水中漂浮,如图甲所示.用刻度尺测出此时水盆内水的深度为h1.将鹅卵石放在塑料碗中,装有鹅卵石的塑料碗仍在水中漂浮,如图乙所示.用刻度尺测出此时水盆内水的深度为h2,将塑料碗中的鹅卵石放入水盆中,如图丙所示.用刻度尺测出此时水盆内水的深度为h3,求ρ石 =?? ? .
22. 底面积为50cm 2的平底圆柱形容器内盛满某种液体后,放置于水平桌面的中央(容器壁厚度不计),已知液体的压强与深度的关系如图1所示.现用轻质细线提起一个质量为80g的实心球缓慢浸没于容器内的液体中,如图2所示,待球静止后,擦干容器外壁,已知细线给球的拉力为0.5N,剪断细线,实心球下沉到容器底部,此时容器对桌面的压强比只盛满液体容器对桌面的压强增大了 pa.(g取10N/kg)
23. 一个土密度计如图所示,其刻度部分的A、B、C三点,AB=2cm,AC=6cm.将密度计放在酒精(ρ酒精=0.8×103kg/m3)中时,液面位置恰好在A点,将密度计放在水中时(ρ水=1.0×103kg/m3),液面位置恰好在B点,当密度计放在某种液体中时,液面位置恰好在C点,则这种液体的密度是????kg/m3.
24. 如图所示的木块浸没在水中,细线对木块的拉力是2N.剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加1N向下的压力时,木块有20cm3的体积露出水面.求木块的密度 .(g取10N/kg)
?
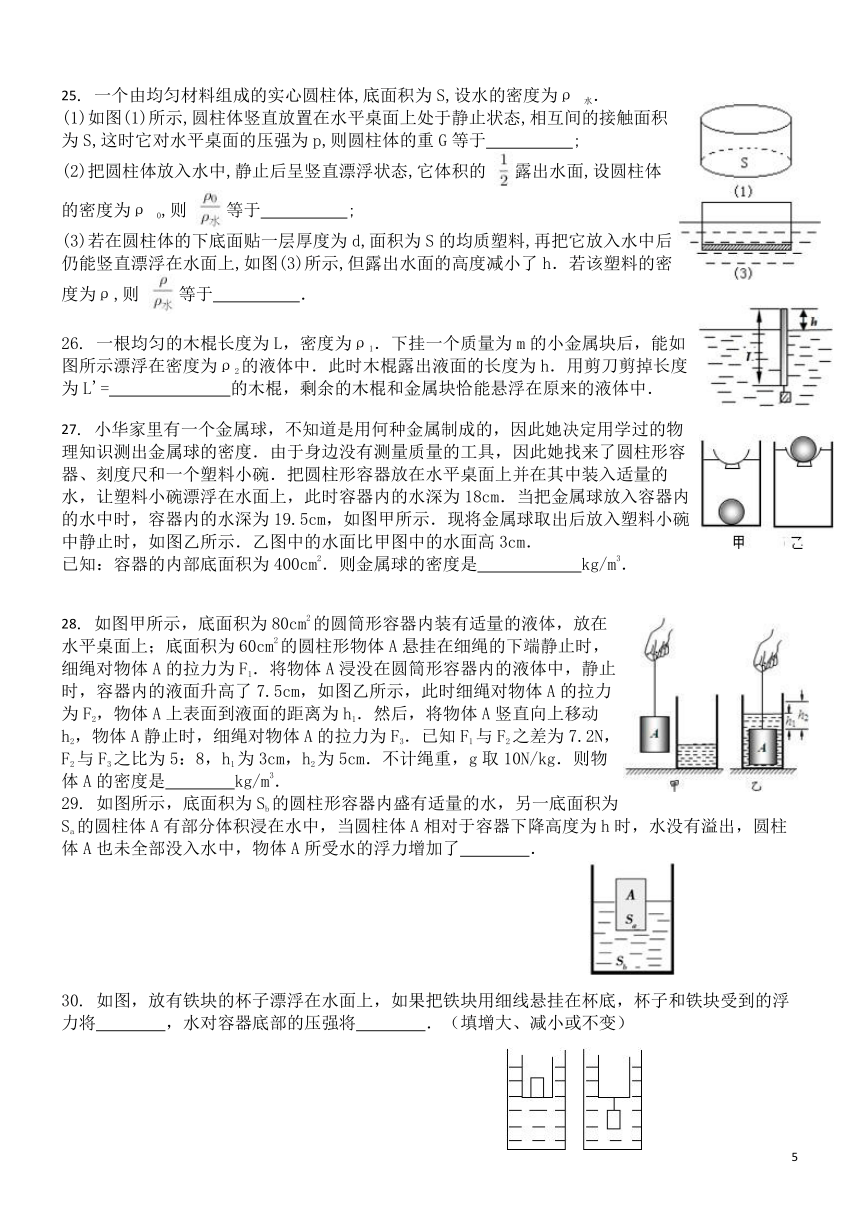
25. 一个由均匀材料组成的实心圆柱体,底面积为S,设水的密度为ρ 水. (1)如图(1)所示,圆柱体竖直放置在水平桌面上处于静止状态,相互间的接触面积为S,这时它对水平桌面的压强为p,则圆柱体的重G等于 ; (2)把圆柱体放入水中,静止后呈竖直漂浮状态,它体积的 露出水面,设圆柱体的密度为ρ 0,则 等于 ; (3)若在圆柱体的下底面贴一层厚度为d,面积为S的均质塑料,再把它放入水中后仍能竖直漂浮在水面上,如图(3)所示,但露出水面的高度减小了h.若该塑料的密度为ρ,则 等于 .
26. 一根均匀的木棍长度为L,密度为ρ1.下挂一个质量为m的小金属块后,能如图所示漂浮在密度为ρ2的液体中.此时木棍露出液面的长度为h.用剪刀剪掉长度为L'= 的木棍,剩余的木棍和金属块恰能悬浮在原来的液体中.
27. 小华家里有一个金属球,不知道是用何种金属制成的,因此她决定用学过的物理知识测出金属球的密度.由于身边没有测量质量的工具,因此她找来了圆柱形容器、刻度尺和一个塑料小碗.把圆柱形容器放在水平桌面上并在其中装入适量的水,让塑料小碗漂浮在水面上,此时容器内的水深为18cm.当把金属球放入容器内的水中时,容器内的水深为19.5cm,如图甲所示.现将金属球取出后放入塑料小碗中静止时,如图乙所示.乙图中的水面比甲图中的水面高3cm. 已知:容器的内部底面积为400cm2.则金属球的密度是?? ? kg/m3.
28. 如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是????kg/m3.
29. 如图所示,底面积为Sb的圆柱形容器内盛有适量的水,另一底面积为Sa的圆柱体A有部分体积浸在水中,当圆柱体A相对于容器下降高度为h时,水没有溢出,圆柱体A也未全部没入水中,物体A所受水的浮力增加了????.
30. 如图,放有铁块的杯子漂浮在水面上,如果把铁块用细线悬挂在杯底,杯子和铁块受到的浮力将????,水对容器底部的压强将????.(填增大、减小或不变)
参考答案
1. -------------------------------------------------------------------------------
C
根据物体的漂浮条件即可判断,漂浮的物体受到的浮力等于其重力.
解:如果将A从木块上拿下后悬挂在木块下面,因为漂浮的物体受到的浮力等于其重力; 铁块A和木块排开水的重力等于A和木块的重力,前后无变化,所以液面不会上升也不会下降. 故选C.
2. -------------------------------------------------------------------------------
【答案】
C
试题分析:设圆柱形容器的重为G1,容器中液体的重为G2,金属球的重为G3,容器的底面积为S,图甲容器对桌面的压强为p1,图乙容器对桌面的压强为p2,图丙容器对桌面的压强为p3,金属球所受浮力是F浮,则p1=F1/S=(G1+G2)/S , p2=F2/S=(G1+G2+F浮)/S ,p3=F3/S=(G1+G2+G3)/S ,所以金属球所受浮力F浮=(p2-p1)S =(600Pa-500Pa×0.01m2=1N;金属球的重G3=(p3-p1)S =(1500Pa-500Pa×0.01m2=10N;金属球的体积V=G3/gp=10N/(10N/Kg×8×103Kg/m3)=1.25×10-4m3=125cm3;因为金属球浸没在液体中,V排=V物,,所以由G=mg=ρ物V物g,F浮=G排=ρ液gV排,可得:ρ液/ρ物=F浮/G,即ρe =F浮ρ物/G=(1N×8×103Kg/m3)/10N=0.8×103Kg/m3=0.8g/cm3;因为由图丙可知,金属球在重力、浮力和支持力的作用下处于平衡状态,所以金属球对容器底部的压力等于它所受的支持力为10N-1N=9N。故选C
考点:力的平衡;压强;浮力
3. -------------------------------------------------------------------------------
解:比较甲乙两图可知,金属块A的重力为G=ρ 水g(H 2-H 1)S 容; 比较乙丙可知,金属块A受到的浮力ρ 水gV A=ρ 水g(h 1-h 2)S; 所以A的体积为V A=(h 1-h 2)S; A的密度为ρ= = = =7.5×10 3kg/m 3; 故答案:7.5×10 3:.
比较甲乙两图可知,烧杯两次受到的浮力之差就是金属块A的重力;进一步求出A的质量; 比较乙丙可知,根据烧杯两次受到的浮力之差可以求出A的体积; 最后利用密度公式求出密度的大小.
4. -------------------------------------------------------------------------------
【答案】(1)知道两种情况下杯底受到的压强差,根据液体压强公式求杯内水面下降的高度,从而可求出金属块排开水的体积,也就可以求出金属块的体积; (2)利用称重法F浮=G+F示分别得出一个方程,而金属块重相同,求出两种情况下金属块受到的浮力,又知道F1,据此求出图乙弹簧测力计的示数; (3)根据ρ==求出金属块的密度.
(1)∵p=ρgh, ∴水面降低的高度: △h===5×10-3m, 金属块体积排开水的体积: V水=S△h=100×10-4m2×5×10-3m=5×10-5m3, ∵V水=, ∴V金=4×5×10-5m3=2×10-4m3,故A不正确; (2)在图甲和图乙中,金属块受力如图1和2所示: 由于两次金属块都处于平衡状态,则有: F1+F浮=G,F2+F浮′=G; 图甲中金属块受到的浮力为: F浮=ρ水gV物=1×103kg/m3×10N/kg×2×10-4m3=2N, ∴金属受到的重力为G=3.4N+2N=5.4N,故D不正确; 图乙中物体受到的浮力为: F浮′=F浮=1.5N, ∴F2=5.4N-1.5N=3.9N,故B不正确; (3)金属的密度为: ρ====2.7×103kg/m3,故C正确. 故选C.
5. -------------------------------------------------------------------------------
【答案】当物体A有的体积露出水面时,筒中水的深度比图甲中水的深度下降了0.4cm,可求出A的体积;进一步求出A的高度,根据公式P=ρgh求出水在物体A底面处产生的压强;根据浮力公式求出A完全浸没时受到的浮力和的体积露出水面时受到的浮力;根据拉力的大小求出A的重力;进一步求出A的质量,根据密度公式求出A的密度. 由题意可得:V=S容△h; 所以A的体积V=S容△h×=50×10-4m2×0.004m×=5×10-5m3; A的高度h===0.05m; 当物体A有的体积露出水面时,水在物体A底面处产生的压强为P=ρgh=1000kg/m3×10N/kg××0.05m=300Pa; 此时物体A所受的浮力为F浮=ρgV=1000kg/m3×10N/kg××5×10-5m3=0.3N; 物体A的重力为G=F+F浮=4N+0.3N=4.3N;A的质量m===0.43kg; A的密度ρA===8.6×103kg/m3=8.6g/cm3; A全部浸没水中细绳对物体的拉力为F拉=G-F浮1=G-ρgV=4.3N-1000kg/m3×10N/kg×5×10-5m3=3.8N; 故选D.
6. -------------------------------------------------------------------------------
B
1,根据试管内外液面的几何关系:试管内液面上升的高度,试管底面下降的高度,容器液面上升的高度间的关系分析. 2,根据试管下降增加的排开水的体积等于容器内水上升增加的体积及试管横截面积与容器横截面积之比为1:5,求出:试管中液体上升的高度H 0,试管底部应再下沉的深度H 1,因试管下沉容器液面上升的高度H 2间关系. 3,根据物块完全浸没在该试管水中,重新排开的水重等于新加入的物体重力,可求出物体的密度.
解:设试管底面积为S 1,容器底面积S 2,物块完全浸没在该试管水中后,试管中液体上升的高度是H 0,试管底部应再下沉的深度H 1,因试管下沉容器液面上升的高度H 2, 试管内物块体积V 物=S 1H 0 G 物=ρ 物gV 物=ρ 物gS 1H 0 试管增加的浮力F 浮=ρ 水gS 1(H 1+H 2) 容器底部增加的压力F 压=ρ 水gS 2H 2 因为试管放入物块后,试管处于漂浮状态 所以:放入物块的重量G 物=试管增加的浮力F 浮=容器底部增加的压力F 压 ρ 物gS 1H 0=ρ 水gS 1(H 1+H 2)=ρ 水gS 2H 2 依题意有S 2=5S 1,代入ρ 水gS 1(H 1+H 2)=ρ 水gS 2H 2,得H 1=4H 2,H 2=0.25H 1 因试管内水面与容器底部的距离都为h,所以H 0=H 1 ρ 物gS 1H 0=ρ 物gS 1H 1=ρ 水gS 1(H 1+H 2)=ρ 水gS 1(H 1+0.25H 1) 则ρ 物=1.25ρ 水=1.25×10 3kg/m 3. 故选B.
7. -------------------------------------------------------------------------------
C
(1)阿基米德原理:浸在液体中的物体受到的浮力等于物体排开的液体受到的重力; (2)蜡烛密度大于酒精的密度,在酒精中完全没入,根据浮力求出蜡的体积,从而求出蜡块的质量; (3)当蜡块放入水中时,由于蜡的密度小于水的密度,因此它在水中漂浮,受到的浮力等于蜡块的重力.
解:(1)蜡的密度比酒精的密度大,在酒精中下沉,完全浸没在酒精中,排开的酒精的体积就是蜡块的体积; 所以蜡块体积V 蜡=V 排= = =5cm 3; 蜡块的质量m 蜡=ρ 蜡V 蜡=0.9g/cm 3×5cm 3=4.5g. (2)由于蜡的密度比水的密度小,在水中漂浮,因此浮力等于蜡的重力,则排开水的质量和蜡块的质量相等,即4.5g. 故选C.
8. -------------------------------------------------------------------------------
本题可采用假设法求解,可分别假设物体在水中可能处的状态,根据阿基米德原理和物体的浮沉条件可知物体在酒精中的状态,由此可选出可能的情况.
解:,,假设物体在水中漂浮,则由物体的浮沉条件可得,物体重为,而在酒精中受到的浮力为,故在酒精中应下沉,不能漂浮,故错,正确; ,假设在水中悬浮,则由物体的浮沉条件可得,物体受到的浮力等于物体重为,而在酒精中受到的浮力为,故在酒精中下沉,不能漂浮,故错; ,假设它在水和酒精中都处于沉入底部,全部排开液体的状态,则它受到的浮力分别是:,; ,而现在是,故错. 故选.
当题目中有多个问题相关联时,可以先假设其中一种情况成立,由此再利用所学知识进行推理,可得出另外的情况是否成立.
9. -------------------------------------------------------------------------------
【答案】根据阿基米德原理知道,水受到水的浮力等于排开水的重,若两水面相平,弹簧测力计示数会为零.现在弹簧测力计的示数不为0,袋内水没有全浸入,据此分析判断. 若袋内水面与袋外水面相平,则排开水的体积等于袋内水的体积,根据阿基米德原理,此时排开水的重力等于袋内水的重力,所以测力计的示数应为零.而题中测力计示数为7N,说明袋内水没有全浸入水中,袋内水面比袋外水面高. 故选A.
10. -------------------------------------------------------------------------------
【解答】解:设P浸入液体的深度为h,P的横截面积为S1;液面至a的深度为H,a的横截面积为S2; 绳子对a的拉力: T1=F浮-G1=ρgS1h-G1; 能拉开a需要的最小力: T2=F压+GA=ρgHS2+G2; 要让水能自动从管中流出,T1≥T2, 即:ρgS1h-G1≥ρgHS2+G2, ∴单独由浮筒P的质量很小、浮筒P的浮力足够大、盖子a比浮筒轻不能满足T1≥T2,故AC都错; ∵ρgS1h-G1≥ρgHS2+G2, ∴ρgS1h>ρgHS2, ∴S1h>HS2, ∵h<H, ∴S1>S2,故B正确,D错误. 故选B.
【分析】对浮筒P进行受力分析,受到水的浮力F浮、重力G1、绳子的拉力T1,F浮=T1+G1; 对盖子a进行受力分析,受到重力G2、水的压力F压、绳子的拉力T2,盖子受到的拉力T2=G2+F压; 要让水能自动从管中流出,T1≥T2,即:F浮-G1≥G2+F压,据此分析判断.
11. -------------------------------------------------------------------------------
12. -------------------------------------------------------------------------------
C
(1)小球A漂浮在甲溢水杯液体中,小球受到的浮力等于重力,据此判断小球A的质量; (2)小球B浸没在乙溢水杯液体中,ρ B大于ρ 2,小球A将下沉,受到的浮力小于重力,据此判断小球B的质量是不是30g;根据小球A与小球B体积之比是1:2;求出ρ 1与ρ 2的关系.
解:A,∵小球A漂浮在甲溢水杯液体中,小球受到的浮力等于重力,由F 浮=G 排=G A,可得小球A的质量为36g;故A错 B,小球A漂浮在甲溢水杯液体中,F 浮′=G 排′=m 排′g=ρ 1V 排g= ρ 1V Ag=36×10 -3kg×g, V A= ∵小球浸没在液体中,并下沉, ∴ρ B大于ρ 2, ∴F 浮=G 排=m 排g<G B=m Bg, ∴小球的B质量:m B>m 排=30g,故B错; C,小球B的体积: V B= = ∵V A:V B=1:2, 即: : = , ∴ρ 1:ρ 2=3:1.故C正确; D,A球质量就等于甲中溢出水的质量,而B球的质量未知所以无法求两球密度之比. 故选C.
13. -------------------------------------------------------------------------------
D
【分析】(1)四个相同的木块,密度相同,组合在一起时的密度仍与一个的相同,根据组合在一起时露出液面的高度为L/2,说明木块的密度小于水的密度,根据浮沉条件木块能漂浮在水面上。
(2)由组合成整体时露出液面的高度L/2可以计算得出水的密度与木块密度的关系。由这个密度关系可以得出分散之后各木块露出液面的高度。
【解答】由四个相同的木块组合在一起时处于漂浮状态可知木块的密度小于水的密度,所以当胶水溶于水木块分散后每块小木块由于密度小于水,也都将漂浮于水面。故A、B选项错误。 根据组合时露出水面的高度为L/2,可知露出液面的体积占组合木块总体的1/4,排开液体的体积是3/4。由于漂浮时浮力=重力,F=G总 , ρ水g(3/4)V木=ρ木gV木 , 所以(3/4)ρ水=ρ木。当木块分散后,由水和木块的密度关系可知,每个小木块都将有3/4的体积浸入水中,有1/4体积露出水面,由木块程立方体可知,将有1/4的高度露出水面,D选项正确。 故选D
14. -------------------------------------------------------------------------------
15. -------------------------------------------------------------------------------
【答案】因为ρ′>ρ,一开始小球将下沉,因为液体密度随深度而增大(ρ=ρ+kh),当液体的密度等于小球的密度时,小球将悬浮,据此求出h大小. 由题知,ρ′>ρ,一开始小球在液体中下沉,随着深度增加,液体的密度增加,当液体的密度等于小球的密度时,小球将悬浮, 设悬浮时的深度为h,则液体的密度ρ液=ρ+kh,则ρ′=ρ+kh,解得h=. 故选D.
16. -------------------------------------------------------------------------------
【答案】已知冰块与容器底部相接触并且相互间有压力,可以得出F浮=ρ水v排g<G冰,再根据冰化成水后质量(重力)不变,得出冰化成的水的体积与冰排开水的体积的关系,从而确定水面的升降.
∵冰熔化前,F浮+F支=G冰, ∴F浮=ρ水v排g<G冰,-------① 冰化水后,G冰=G水, 即:ρ冰v冰g=ρ水v水g,-------② 由①②可得: ρ水v排g<ρ水v水g, 即:冰熔化为水的体积大于排开水的体积, ∴冰熔化后,水面将上升. 故答案为:升高. 17. -------------------------------------------------------------------------------
;
18. -------------------------------------------------------------------------------
解:由“若把球放在盒内密封后,放入密度为ρ的液体中金属盒有h 1的高度露出液面,如图甲所示”可得ρL 2(L-h 1)=m 盒+m 球…①; 由乙图可得ρV 球+ρL 2(L-h 2)=m 盒+m 球…②; 由丙图可得ρL 2(L-h 3)=m 盒…③, 由①-③得m 球=ρL 2(h 3-h 1); 由①-②得V 球=L 2(h 2-h 1); 则金属球的密度ρ 球= = = ρ. 故答案为: ρ.
根据物体的浮沉条件分别列出甲,乙,丙三图的关系式,三式联立求得金属球的质量和体积表达式,再利用ρ= 即可求得金属球的密度.
19. -------------------------------------------------------------------------------
解:(1)∵铝槽漂浮, ∴铝槽受到的浮力: F浮=G=mg=0.54kg×10N/kg=5.4N; (2)由题知,铝槽排开水的体积: v排=sh=100×10-4m2×0.027m=2.7×10-4m3, ∵F浮=ρ液v排g, ∴液体的密度: ρ液===2×103kg/m3; (3)铝槽浸没时排开液体的体积: v排′=v铝===2×10-4m3, 液面上升的高度: h′===0.02m, 沉入前后液面变化值: △h=h-h′=0.027m-0.02m=0.007m 沉入前后液体对容器底的压强变化值: △p=ρ液g△h=2×103kg/m3×10N/kg×0.007m=140Pa. 故答案为:140.
(1)知道铝槽的质量,利用重力公式求铝槽重,又因为铝槽漂浮,利用漂浮条件求铝槽受到的浮力; (2)知道液面上升的高度,可求排开水的体积,利用阿基米德原理求液体的密度; (3)知道铝槽质量和密度,求铝的体积,也就知道铝槽浸没液体中排开液体的体积,又知道容器底面积,求液面上升的高度,和铝槽漂浮时上升的高度比较,利用液体压强公式求沉入前后液体对容器底的压强变化值.
20. -------------------------------------------------------------------------------
【解答】解:由甲、丙图可知,石块放在木块上时比木块多排开液体的体积: △V排=(h1-h3)S=(0.16m-0.1m)×50×10-4m2=3×10-4m3, 木块受到的浮力差: △F=ρ液g△V排=ρ液×10N/kg×3×10-4m3, ∵木块和石块放在木块上时的木块漂浮, ∴G石=ρ液×10N/kg×3×10-4m3; 由乙丙两图可知: 小石块的体积: V石=(h2-h3)S=(0.12m-0.1m)×50×10-4m2=1×10-4m3, 在图乙中,石块受到的浮力: F浮乙=ρ液gV石=ρ液×10N/kg×1×10-4m3, 小石块对杯底的压力: F=G-F浮乙=ρ液×10N/kg×3×10-4m3-ρ液×10N/kg×1×10-4m3=1.6N, 解得: ρ液=0.8×103kg/m3, 小石块的重力: G石=0.8×103kg/m3×10N/kg×3×10-4m3=2.4N, 小石块的质量:
m石==0.24kg, 小石块的密度: ρ石===2.4×103kg/m3. 故答案为:2.4×103kg/m3.
【分析】图甲比图丙多排开液体的体积是△V=(h1-h3)S,说明图甲中木块和小石块受到的总的浮力比图丙中木块受到的浮力要大:△F=ρ液g△V; 两次都是漂浮,总浮力都等于物体自身的重力,所以增大的浮力刚好等于小石块的重力; 图乙比图丙多排开液体的体积(h2-h3)S为小石块的体积, 在图乙中,小石块受到的浮力为F浮=ρ液gV石,小石块受到的重力与浮力之差就是石块对杯底的压力,据此求出液体的密度,求出小石块的质量,再利用密度公式求小石块的密度.
21. -------------------------------------------------------------------------------
【答案】(1)测量物体密度,一般应用的原理都是ρ=,如何得到鹅卵石的质量和体积是实验的关键. ①如图甲,在水盆内放入适量水,将塑料碗轻轻放入水中漂浮,用刻度尺测出此时水盆内水的深度为h1; 如图乙,将鹅卵石放在塑料碗中,装有鹅卵石的塑料碗仍在水中漂浮,用刻度尺测出此时水盆内水的深度为h2,设水盆的底面积为S,两次深度之差与底面积的乘积就是鹅卵石漂浮时排开水的体积;已知水的密度和鹅卵石漂浮时排开水的体积,可以得到鹅卵石漂浮排开水的质量,也就是鹅卵石的质量; ②如图丙,将塑料碗中的鹅卵石放入水盆中,用刻度尺测出此时水盆内水的深度为h3,h3与h1之差与水盆底面积的乘积就是鹅卵石浸没时排开水的体积,也就是鹅卵石的体积. (2)已知鹅卵石的质量和体积,利用ρ=,可得到其密度. 设水盆的底面积为S, 鹅卵石漂浮时排开水的体积V=(h2-h1)S, 鹅卵石漂浮时排开水的质量m=ρ水V=ρ水(h2-h1)S, 鹅卵石的质量m石=m=ρ水V=ρ水(h2-h1)S, 鹅卵石的体积V石=(h3-h1)S, 鹅卵石的密度ρ石===ρ水.
故答案为:ρ水.
22. -------------------------------------------------------------------------------
解:剪断细线,实心球下沉到容器底部时, 容器对桌面的压力增大值: △F 压=F 线=0.5N, 容器对桌面的压强增大值: △p= = =100Pa. 故答案为:100.
当剪断细线实心球下沉到容器底部时,对桌面的压力比只盛满液体对桌面的压力增大值为细线给球的拉力,再利用压强公式求出容器对桌面压强的增大值.
23. -------------------------------------------------------------------------------
【解答】解:密度计的重力不变,密度计处于漂浮状态,浮力等于重力,即浮力也不变. 设A、B、C三点显示的密度分别为ρ1、ρ2、ρ3; 则可得:ρ1gV1=ρ2gV2=ρ3gV3=G 约去g可得:ρ1V1=ρ2V2=ρ3V3=m V1-V2=-; V1-V3=-; 由题意知,V1-V2=s?AB,V1-V3=s?AC,又AB=2cm,AC=6cm. ∴3(V1-V2)=V1-V3; 即:3( -)=-; ∴3(-)=- 将ρ1及ρ2代入,可得: 3(-)=- 解得:ρ3=2×103kg/m3. 故答案为:2×103kg/m3.
【分析】因为已知密度计的测量范围,则可根据物体的浮沉条件得出液面在A和B点时密度计排开水的体积,则利用AC、CB两段的体积关系可得出液面在中点时的所测密度与液面分别在A、B两点时的密度关系,则可求得液面在C点时的所示密度.
24. -------------------------------------------------------------------------------
【答案】
木块密度为0.6×103kg/m3.
分别对木块所处的几种状态作出受力分析.
如图(a)(b)(c).
(a)(b)(c)
图(a)中,木块受拉力F1,重力和浮力.
图(b)中,细线剪断,木块处于漂浮状态,设排开水的体积为V排.
图(c)中,将露出水面的部分切去后,木块仍漂浮,这时再
施加F2=1 N的压力,仍有部分体积露出水面.
已知:F1=2N,F2=1N,V′=20cm3—2×10—5m3
求:水
解 根据三个图,木块均静止,分别列出受力平衡过程
将公式中各量展开,其中V排指图(b)中排开水的体积.
代入数值事理,过程中用国际单位(略)
水V—木V=
水V排—木V
(水V排—木V排)=+水×2×10—5
约去V排和V,求得:水=0.6×103kg/m3
25. -------------------------------------------------------------------------------
解:(1)圆柱体的重力:G=F=pS; (2)∵圆柱体漂浮 ∴F 浮=G ρ 水g V=ρ 0gV 则 = ; (3)∵圆柱体和塑料共同漂浮 ∴F 浮′=G ρ 水g(Sd+ V+Sh)=ρ 0gV+ρgSd ρ 水(Sd+ V+Sh)=ρ 水V+ρSd 则 = . 故答案为:(1)pS;(2) ;(3) .
(1)水平桌面上静止的物体,桌面受到的压力等于物体的重力,因此根据F=pS即可求出重力的大小; (2)根据物体漂浮时,浮力等于重力即可求出圆柱体和水的密度之比; (3)利用浮力等于重力即可求出塑料和水的密度之比.
26. -------------------------------------------------------------------------------
解:设木棒横截面积为s,小金属块在液体中受到的浮力为,
小金属块的受到重力:,
∵原来木棒漂浮在液体中,
∴,
即:ρ_,--------①
∵剪掉L'后,木棒悬浮在液体中,
∴'=G',
即:ρ_,--------②
由①-②得:
ρ_{2}(L-h)sg-ρ_{2}(L-L')sg=ρ_{1}Lsg-ρ_{1}(L-L')sg,
解得:L'=.
故答案为:
分两种状态分析:一、原来漂浮,根据漂浮条件列出受到浮力等于重力的关系式;二、剪掉L'后的悬浮,根据悬浮条件列出受到浮力等于重力的关系式;联立方程求解.
27. -------------------------------------------------------------------------------
【答案】根据密度公式ρ=进行分析,先根据放球前的水深18cm和放球后水深19.5cm以及容器的内部底面积求出球的体积;再根据碗漂浮时水面的高度、球和碗共同漂浮时水面的高度以及容器的底面积求出排开水的体积,然后结合阿基米德原理球的重力等于排开水的重力即可求出球的质量,知道金属球的质量和体积便可求出金属球的密度. 金属球的体积:V=Sh=400cm2×(19.5cm-18cm)=600cm3=6×10-4m3; 球和碗同时漂浮时,金属球排开水的体积V′=400cm2×(19.5cm+3cm-18cm)=18×10-4m3; 金属球的质量m=m排=ρ水V′=1.0×103kg/m3×18×10-4m3=1.8kg; 金属球的密度ρ===3×103kg/m3. 故答案为 3×103.
28. -------------------------------------------------------------------------------
【解答】解:①v物=80cm2×7.5cm=600cm3, 则物体A的高度为:hA===10cm; 因为物体在空气中静止时,绳子的拉力等于物体的重力即F1, 又因为F1与F2之差为7.2N, 因此物体在液体中受到的浮力等于7.2N; 即7.2N=ρ液gv物 7.2N=ρ液×10N/kg×600×10-6m3 ρ液=1.2×103kg/m3; ②如图乙,当物体A全部浸没在液体中时,以其底面所在平面为参考面,设其位置为e,那么在提出物体A时,在位置e以下的部分体积不再发生变化,因此不做考虑; 那么当物体A提起h2时,位置e以上的总体积保持不变,若设物体提起h2时,物体A在液面上的部分高度为xcm,那么以这个总体积不变作为等量关系,可列出: S容器?(hA+h1)=S物?x+S容器?(hA+h2-x),即: 80cm2×(10cm+3cm)=60cm2×x+80cm2×(10cm+5cm-x) 解得:x=8; 那么此时,物体A浸入液体中的高度为:h=10cm-8cm=2cm. ③已知:完全浸没时细绳对物体A的拉力为F2与提升高度h2时细绳对物体A的拉力为F3的比值为 5:8,得: (F1-F浮):(F1-ρ液gv排)=5:8,即: (ρ物gs物hA-ρ液gs物hA):(ρ物gs物hA-ρ液gs物h)=5:8 解得:ρ物=ρ液=×1.2×103kg/m3=2.8×103kg/m3; 故答案为:2.8×103.
【分析】先根据容器的底面积和上升的高度求出物体的体积,然后根据浮力的大小(F1与F2之差)求出液体的密度; 若求物体的密度,就必须利用“F2与F3之比为5:8”,物体全部浸没时,F2为F1与F浮的差,而将物体提升h2后,F3为F2与此时物体所受浮力的差,那么求出提升h2后,物体A排开液体的体积,即浸没在液体中部分的体积为解答此题的关键; 首先将研究对象简化,在图乙中,物体完全浸没时,以物体A的底面所在平面为参考面,在提升物体前后,此面以下的液体体积不会发生变化,所以可以先不予考虑;那么参考面以上部分,物体和液体的体积总和在提升物体前后始终不变,可利用这个等量关系来列出方程求得提升物体后,物体浸没在液体中的高度,进而可求出这部分的体积大小,即:排开液体的体积,由此整个题目的未知量全部求出.
29. -------------------------------------------------------------------------------
【解答】解:圆柱体A原来排开水的体积为V排,见图, 则V排=Sah′, 圆柱体A下降h后排开水的体积为V排′, 则V排′=Sa(h+h′+△h)=Sah′+Sa(h+△h), ∴排开水的体积的变化为:△V排=V排′-V排=Sah′+Sa(h+△h)-Sah′=Sa(h+△h), 两液面的变化为:△h==, 解得:△h=h, 则:△V排=Sb△h=h, 因此圆柱体A所受水的浮力增加为:△F浮=ρ水g△V排=ρ水gh. 故答案为:ρ水gh.
【分析】首先设圆柱体A原来浸在水中的深度为h′,放入圆柱体A后两液面的变化为△h,再利用公式V=Sh计算出圆柱体A原来排开水的体积和圆柱体A下降h后排开水的体积,从而可以计算出排开水的体积的变化,最后再利用公式F浮=ρ液V排g计算浮力的变化.
30. -------------------------------------------------------------------------------
【解答】解: ①把铁块和杯子看做一个整体,根据漂浮状态下F浮=G物,由于铁块和杯子的重力和始终不变,所以杯子和铁块受到总浮力不变; ②由阿基米德原理知,杯子和铁块受到的浮力为F浮=ρ液gV排,因为总F浮一直保持不变,且ρ液和g均不变,所以V排也不变,因此前后水面的高度h是不变的, 又因为P底=ρ液gh,ρ液gh始终不变,所以水对容器底的压强不变. 故答案为:不变;不变.
【分析】①漂浮的物体受到的浮力等于物体的重力.浮力是否变化根据重力是否变化判断; ②液体对容器底的压强用公式P=ρgh分析.
选择题
1. 如图1,在一个较大的容器中盛有水,水中放有一个木块,木块上面放有铁块A,此时木块漂浮;如果将A从木块上拿下后悬挂在木块下面如图2,并放入水中,当木块和A都静止时(水未溢出),下面说法正确的是( ) A. 容器中水面上升 B. 容器中水面下降 C. 容器中水面不变 D. 无法判断
2. 盛有液体的圆柱形容器置于水平桌面上,如图甲所示,容器对桌面的压强为500Pa;用细线拴一金属球,将金属球浸没在液体中,如图乙所示,容器对桌面的压强为600Pa;将细线剪断,金属球沉到容器底部,如图丙所示,容器对桌面的压强为1500Pa。已知:容器的底面积为100cm2,金属球的密度为8g/cm3,g取10N/kg。则下列判断正确的是( ) A. 金属球所受浮力是6N B. 金属球的体积是100cm3 C. 液体的密度是0.8g/cm3 D. 金属球对容器底部的压力是10N
3. 圆柱形容器中装有适量的水,将一只装有配重的薄壁长烧杯放入圆柱形容器的水中,烧杯静止时容器中水的深度H 1为20cm,如图甲所示.将金属块A吊在烧杯底部,烧杯静止时露出水面的高度h 1为5cm,容器中水的深度H 2为35cm,如图乙所示.将金属块A放在烧杯中,烧杯静止时露出水面的高度h 2为1cm,如图丙所示.已知圆柱形容器底面积为烧杯底面积的2倍.则金属块A的密度为 kg/m 3.
4. 底面积为100cm2的烧杯中装有适量水.当金属块浸没在水中静止时,如图甲所示,弹簧测力计的示数F1=3.4N,水对杯底的压强为p1;当金属块总体积的1/4露出水面静止时,如图乙所示,弹簧测力计的示数为F2,水对杯底的压强为p2;若p1、p2之差为50Pa,g取10N/kg,则( ) A. 金属块的体积V金是2×10-3m3 B. 弹簧测力计的示数F2是5.4N C. 金属块的密度是2.7×103kg/m3 D. 金属块受到的重力是6.8N
5. 如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体A浸没在水中,细绳对物体的拉力为F拉.如图乙所示,当物体A有的体积露出水面时,作用在物体A上的竖直向上的拉力为4N,筒中水的深度比图甲中水的深度下降了0.4cm,此时,物体A所受的浮力为F浮,水在物体A底面处产生的压强为p.g取10N/kg,悬挂物体的细绳的质量忽略不计.( ) A. F拉的大小为4.8N B. F浮的大小为0.2N C. ρA的大小为8g/cm3 D. p的大小为300Pa
6. 如图甲所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h,试管壁粗细均匀,厚度不计;现将一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好仍为h,如图乙所示,若试管横截面积与容器横截面积之比为1:5,则下列说法正确的是( ) A. 放入的物块密度为5×10 3kg/m 3 B. 放入的物块密度为1.25×10 3kg/m 3 C. 放入的物块密度为2.25×10 3kg/m 3 D. 小试管与容器内水面变化的高度相等
7.把一根蜡烛放入盛满酒精的容器中,溢出酒精的质量为4克,若把蜡烛放入盛满水的容器中,则溢出水的质量为(蜡烛的密度为0.9克/立方厘米)( ) A. 4克 B. 5克 C. 4.5克 D. 3.6克
8. 将一实心物体先后投入足量的水和酒精中,物体静止时,所受浮力分别为和,判定物体在水酒精中的浮沉状态可能是( ) A、在水中漂浮,在酒精中漂浮 B、在水中漂浮,在酒精中沉底 C、在水中悬浮,在酒精中漂浮 D、在水中沉底,在酒精中沉底
9. 如将一只盛有水的薄塑料袋,用细线扎紧袋口,用弹簧测力计测得其重力为9N,再将这个装水的塑料袋浸入水中,当弹簧测力计示数为7N时,袋内水面与袋外水面相比较( ) A. 塑料袋内水面比袋外水面高 B. 塑料袋内水面比袋外水面低 C. 塑料袋内水面与袋外水面相平 D. 塑料袋内水面与袋外水面高低无法判断
10. 如图,厕所里自动冲洗的水箱里有一个圆柱形的浮筒P,下水管口有一塞子a,两者用短链相连,若水箱的深度足够,要实现自动定时冲洗,则( ) A. 只要浮筒P的体积足够大 B. 浮筒P的截面必须大于塞子a的截面 C. 只要浮筒P足够轻 D. 浮筒P的截面必须小于塞子a的截面
11. 如图所示,柱形容器的底面积为200cm2,边长为10cm的正方体实心冰块悬浮在油水分层液体中,冰会逐渐熔化,已知浸在分层液体中的物体受到的浮力大小等于它排开所有液体的总重力,ρ油=0.75×103kg/m3,ρ冰=0.9×103kg/m3,下列选项正确的是( ) A. 最初冰块浸在油中的体积是600cm3 B. 冰块完全熔化后,油面下降了0.5cm C. 冰块完全熔化后水对容器底的压强增加了150Pa D. 冰块完全熔化前,逐渐变小的冰块浸在油中的比例逐渐变大
12. 甲溢水杯盛满密度为ρ1的液体,乙溢水杯盛满密度为ρ2的液体.将密度为ρA的小球A轻轻放入甲溢水杯,小球漂浮且有 体积露出液面,甲溢水杯溢出液体的质量是36g.将密度为ρB的小球B轻轻放入乙溢水杯,小球浸没在液体中,并下沉,乙溢水杯溢出液体的质量是30g.已知小球A与小球B体积之比是1:2(g取10N/kg).则下列选项中正确的是( ) A. 小球A的质量为7.2g B. 小球B的质量为30g C. ρ1与ρ2之比为3:1 D. ρA与ρB之比为12:5
13. 4 个边长均为 L 的相同的立方体木块,用胶水(胶水质量不计)粘在一起放入水中,露 出水面的高度为 L/2,如图所示。当胶水溶于水后,木块散开,这时(? )
A. a、b 露出水面高度为 L/2,c、d 为零 B. a、b 露出水面高度为 L/2,c、d 沉入水底 C. a、b、c、d 露出水面高度都是 L/2 D. a、b、c、d 露出水面高度都是 L/4
14.已知A、C均为实心铁块(ρ铁=7.9g/cm3),B为不吸水木块,将A放在B上,B刚好浸没在水中,如图甲;取出A,并将C用轻质细线悬挂在B的底部(C未与容器底部接触,不计操作时带出的水),也能使B刚好浸没,如图乙;柱形容器足够高,且容器底面积是B底面积的三倍,则下列说法中正确的是( ) A. 甲乙两图中,水对容器底部的压强相等
B. A、C两物体的体积之比为69:79 C. 乙图中,剪断BC之间的绳子,水对容器底部压力的变化量等于容器对桌面压力的变化量 D. 乙图中,剪断BC之间的绳子,水面静止时,B相对于容器底部上升的高度等于水面下降的高度
15.一种液体的密度随深度而增大,它的变化规律是ρ1=ρ+kh,式中ρ、k是常数,h表示深度.设深度足够,有一个密度为ρ′的实心小球投入此液体中,且ρ′>ρ,则正确的判断是( ) A. 小球将一沉到底,不再运动 B. 小球将漂浮在液面,不能下沉 C. 小球经过一段运动过程,最终悬浮在深处 D. 小球经过一段运动过程,最终悬浮在深处
如图所示,一块0℃的冰放在盛有0℃的水的容器中.已知冰块与容器底部相接触并相互间有压力,则当冰完全融化为0℃的水后.容器中水面的位置将( ) A. 上升 B. 下降 C. 保持不变 D. 水面的升或降决定于冰和容器内水的体积
填空题
17.在水平桌面上竖直放置一个底面积为S的圆柱形容器,内装密度为 液体,将挂在弹簧秤上体积为V的实心金属球浸没在该液体中(液体未溢出),物体静止时,弹簧秤示数为F;撤去弹簧秤,球下沉并静止于容器底部,此时液体对容器底部的压力为容器底对金属球的支持力的n倍。
求: (1)金属球的密度 ??????????????????????; (2)圆柱形容器内液体的质量 ????????????????。
18.如图所示,边长为L的正方体空心金属盒和实心金属球各一个.若把球放在盒内密封后,放入密度为ρ的液体中金属盒有h 1的高度露出液面,如图甲所示;若把球和盒用细绳相连放入液体中静止后,金属盒有h 2的高度露出液面,如图乙所示;若把球和盒分别放入液体中静止后,金属盒有h 3的高度露出液面,金属球沉入液体底部,如图丙所示.不计细线的重力和体积.金属球的密度ρ球= .
19.如图所示,质量为540g的凹形铝槽,放入底面积为100cm2的圆柱形液体中,铝槽浮在液面上,槽口恰好与液面相平,这时液面上升了2.7cm,若使铝槽沉入液体中,则沉入前后液体对容器底部的压强变化△P= Pa.(已知ρ铝=2.7×103kg/m3;g=10N/kg)
20. 如图甲所示;一个底面积为50cm2的烧杯装有某种液体,把小石块放在木块上,静止时液体深h1=16cm;如图乙所示;若将小石块放入液体中,液体深h2=12cm,石块对杯底的压力F=1.6N;如图丙所示,取出小石块后,液体深h3=10cm.则小石块的密度ρ石为????kg/m3.(g取10N/kg)
21. 小阳想测出一块鹅卵石的密度.他在家中利用刻度尺、口大底小的塑料碗、大烧杯和适量的水进行实验,在烧杯内放入适量水,再将塑料碗轻轻放入水中漂浮,如图甲所示.用刻度尺测出此时水盆内水的深度为h1.将鹅卵石放在塑料碗中,装有鹅卵石的塑料碗仍在水中漂浮,如图乙所示.用刻度尺测出此时水盆内水的深度为h2,将塑料碗中的鹅卵石放入水盆中,如图丙所示.用刻度尺测出此时水盆内水的深度为h3,求ρ石 =?? ? .
22. 底面积为50cm 2的平底圆柱形容器内盛满某种液体后,放置于水平桌面的中央(容器壁厚度不计),已知液体的压强与深度的关系如图1所示.现用轻质细线提起一个质量为80g的实心球缓慢浸没于容器内的液体中,如图2所示,待球静止后,擦干容器外壁,已知细线给球的拉力为0.5N,剪断细线,实心球下沉到容器底部,此时容器对桌面的压强比只盛满液体容器对桌面的压强增大了 pa.(g取10N/kg)
23. 一个土密度计如图所示,其刻度部分的A、B、C三点,AB=2cm,AC=6cm.将密度计放在酒精(ρ酒精=0.8×103kg/m3)中时,液面位置恰好在A点,将密度计放在水中时(ρ水=1.0×103kg/m3),液面位置恰好在B点,当密度计放在某种液体中时,液面位置恰好在C点,则这种液体的密度是????kg/m3.
24. 如图所示的木块浸没在水中,细线对木块的拉力是2N.剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加1N向下的压力时,木块有20cm3的体积露出水面.求木块的密度 .(g取10N/kg)
?
25. 一个由均匀材料组成的实心圆柱体,底面积为S,设水的密度为ρ 水. (1)如图(1)所示,圆柱体竖直放置在水平桌面上处于静止状态,相互间的接触面积为S,这时它对水平桌面的压强为p,则圆柱体的重G等于 ; (2)把圆柱体放入水中,静止后呈竖直漂浮状态,它体积的 露出水面,设圆柱体的密度为ρ 0,则 等于 ; (3)若在圆柱体的下底面贴一层厚度为d,面积为S的均质塑料,再把它放入水中后仍能竖直漂浮在水面上,如图(3)所示,但露出水面的高度减小了h.若该塑料的密度为ρ,则 等于 .
26. 一根均匀的木棍长度为L,密度为ρ1.下挂一个质量为m的小金属块后,能如图所示漂浮在密度为ρ2的液体中.此时木棍露出液面的长度为h.用剪刀剪掉长度为L'= 的木棍,剩余的木棍和金属块恰能悬浮在原来的液体中.
27. 小华家里有一个金属球,不知道是用何种金属制成的,因此她决定用学过的物理知识测出金属球的密度.由于身边没有测量质量的工具,因此她找来了圆柱形容器、刻度尺和一个塑料小碗.把圆柱形容器放在水平桌面上并在其中装入适量的水,让塑料小碗漂浮在水面上,此时容器内的水深为18cm.当把金属球放入容器内的水中时,容器内的水深为19.5cm,如图甲所示.现将金属球取出后放入塑料小碗中静止时,如图乙所示.乙图中的水面比甲图中的水面高3cm. 已知:容器的内部底面积为400cm2.则金属球的密度是?? ? kg/m3.
28. 如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是????kg/m3.
29. 如图所示,底面积为Sb的圆柱形容器内盛有适量的水,另一底面积为Sa的圆柱体A有部分体积浸在水中,当圆柱体A相对于容器下降高度为h时,水没有溢出,圆柱体A也未全部没入水中,物体A所受水的浮力增加了????.
30. 如图,放有铁块的杯子漂浮在水面上,如果把铁块用细线悬挂在杯底,杯子和铁块受到的浮力将????,水对容器底部的压强将????.(填增大、减小或不变)
参考答案
1. -------------------------------------------------------------------------------
C
根据物体的漂浮条件即可判断,漂浮的物体受到的浮力等于其重力.
解:如果将A从木块上拿下后悬挂在木块下面,因为漂浮的物体受到的浮力等于其重力; 铁块A和木块排开水的重力等于A和木块的重力,前后无变化,所以液面不会上升也不会下降. 故选C.
2. -------------------------------------------------------------------------------
【答案】
C
试题分析:设圆柱形容器的重为G1,容器中液体的重为G2,金属球的重为G3,容器的底面积为S,图甲容器对桌面的压强为p1,图乙容器对桌面的压强为p2,图丙容器对桌面的压强为p3,金属球所受浮力是F浮,则p1=F1/S=(G1+G2)/S , p2=F2/S=(G1+G2+F浮)/S ,p3=F3/S=(G1+G2+G3)/S ,所以金属球所受浮力F浮=(p2-p1)S =(600Pa-500Pa×0.01m2=1N;金属球的重G3=(p3-p1)S =(1500Pa-500Pa×0.01m2=10N;金属球的体积V=G3/gp=10N/(10N/Kg×8×103Kg/m3)=1.25×10-4m3=125cm3;因为金属球浸没在液体中,V排=V物,,所以由G=mg=ρ物V物g,F浮=G排=ρ液gV排,可得:ρ液/ρ物=F浮/G,即ρe =F浮ρ物/G=(1N×8×103Kg/m3)/10N=0.8×103Kg/m3=0.8g/cm3;因为由图丙可知,金属球在重力、浮力和支持力的作用下处于平衡状态,所以金属球对容器底部的压力等于它所受的支持力为10N-1N=9N。故选C
考点:力的平衡;压强;浮力
3. -------------------------------------------------------------------------------
解:比较甲乙两图可知,金属块A的重力为G=ρ 水g(H 2-H 1)S 容; 比较乙丙可知,金属块A受到的浮力ρ 水gV A=ρ 水g(h 1-h 2)S; 所以A的体积为V A=(h 1-h 2)S; A的密度为ρ= = = =7.5×10 3kg/m 3; 故答案:7.5×10 3:.
比较甲乙两图可知,烧杯两次受到的浮力之差就是金属块A的重力;进一步求出A的质量; 比较乙丙可知,根据烧杯两次受到的浮力之差可以求出A的体积; 最后利用密度公式求出密度的大小.
4. -------------------------------------------------------------------------------
【答案】(1)知道两种情况下杯底受到的压强差,根据液体压强公式求杯内水面下降的高度,从而可求出金属块排开水的体积,也就可以求出金属块的体积; (2)利用称重法F浮=G+F示分别得出一个方程,而金属块重相同,求出两种情况下金属块受到的浮力,又知道F1,据此求出图乙弹簧测力计的示数; (3)根据ρ==求出金属块的密度.
(1)∵p=ρgh, ∴水面降低的高度: △h===5×10-3m, 金属块体积排开水的体积: V水=S△h=100×10-4m2×5×10-3m=5×10-5m3, ∵V水=, ∴V金=4×5×10-5m3=2×10-4m3,故A不正确; (2)在图甲和图乙中,金属块受力如图1和2所示: 由于两次金属块都处于平衡状态,则有: F1+F浮=G,F2+F浮′=G; 图甲中金属块受到的浮力为: F浮=ρ水gV物=1×103kg/m3×10N/kg×2×10-4m3=2N, ∴金属受到的重力为G=3.4N+2N=5.4N,故D不正确; 图乙中物体受到的浮力为: F浮′=F浮=1.5N, ∴F2=5.4N-1.5N=3.9N,故B不正确; (3)金属的密度为: ρ====2.7×103kg/m3,故C正确. 故选C.
5. -------------------------------------------------------------------------------
【答案】当物体A有的体积露出水面时,筒中水的深度比图甲中水的深度下降了0.4cm,可求出A的体积;进一步求出A的高度,根据公式P=ρgh求出水在物体A底面处产生的压强;根据浮力公式求出A完全浸没时受到的浮力和的体积露出水面时受到的浮力;根据拉力的大小求出A的重力;进一步求出A的质量,根据密度公式求出A的密度. 由题意可得:V=S容△h; 所以A的体积V=S容△h×=50×10-4m2×0.004m×=5×10-5m3; A的高度h===0.05m; 当物体A有的体积露出水面时,水在物体A底面处产生的压强为P=ρgh=1000kg/m3×10N/kg××0.05m=300Pa; 此时物体A所受的浮力为F浮=ρgV=1000kg/m3×10N/kg××5×10-5m3=0.3N; 物体A的重力为G=F+F浮=4N+0.3N=4.3N;A的质量m===0.43kg; A的密度ρA===8.6×103kg/m3=8.6g/cm3; A全部浸没水中细绳对物体的拉力为F拉=G-F浮1=G-ρgV=4.3N-1000kg/m3×10N/kg×5×10-5m3=3.8N; 故选D.
6. -------------------------------------------------------------------------------
B
1,根据试管内外液面的几何关系:试管内液面上升的高度,试管底面下降的高度,容器液面上升的高度间的关系分析. 2,根据试管下降增加的排开水的体积等于容器内水上升增加的体积及试管横截面积与容器横截面积之比为1:5,求出:试管中液体上升的高度H 0,试管底部应再下沉的深度H 1,因试管下沉容器液面上升的高度H 2间关系. 3,根据物块完全浸没在该试管水中,重新排开的水重等于新加入的物体重力,可求出物体的密度.
解:设试管底面积为S 1,容器底面积S 2,物块完全浸没在该试管水中后,试管中液体上升的高度是H 0,试管底部应再下沉的深度H 1,因试管下沉容器液面上升的高度H 2, 试管内物块体积V 物=S 1H 0 G 物=ρ 物gV 物=ρ 物gS 1H 0 试管增加的浮力F 浮=ρ 水gS 1(H 1+H 2) 容器底部增加的压力F 压=ρ 水gS 2H 2 因为试管放入物块后,试管处于漂浮状态 所以:放入物块的重量G 物=试管增加的浮力F 浮=容器底部增加的压力F 压 ρ 物gS 1H 0=ρ 水gS 1(H 1+H 2)=ρ 水gS 2H 2 依题意有S 2=5S 1,代入ρ 水gS 1(H 1+H 2)=ρ 水gS 2H 2,得H 1=4H 2,H 2=0.25H 1 因试管内水面与容器底部的距离都为h,所以H 0=H 1 ρ 物gS 1H 0=ρ 物gS 1H 1=ρ 水gS 1(H 1+H 2)=ρ 水gS 1(H 1+0.25H 1) 则ρ 物=1.25ρ 水=1.25×10 3kg/m 3. 故选B.
7. -------------------------------------------------------------------------------
C
(1)阿基米德原理:浸在液体中的物体受到的浮力等于物体排开的液体受到的重力; (2)蜡烛密度大于酒精的密度,在酒精中完全没入,根据浮力求出蜡的体积,从而求出蜡块的质量; (3)当蜡块放入水中时,由于蜡的密度小于水的密度,因此它在水中漂浮,受到的浮力等于蜡块的重力.
解:(1)蜡的密度比酒精的密度大,在酒精中下沉,完全浸没在酒精中,排开的酒精的体积就是蜡块的体积; 所以蜡块体积V 蜡=V 排= = =5cm 3; 蜡块的质量m 蜡=ρ 蜡V 蜡=0.9g/cm 3×5cm 3=4.5g. (2)由于蜡的密度比水的密度小,在水中漂浮,因此浮力等于蜡的重力,则排开水的质量和蜡块的质量相等,即4.5g. 故选C.
8. -------------------------------------------------------------------------------
本题可采用假设法求解,可分别假设物体在水中可能处的状态,根据阿基米德原理和物体的浮沉条件可知物体在酒精中的状态,由此可选出可能的情况.
解:,,假设物体在水中漂浮,则由物体的浮沉条件可得,物体重为,而在酒精中受到的浮力为,故在酒精中应下沉,不能漂浮,故错,正确; ,假设在水中悬浮,则由物体的浮沉条件可得,物体受到的浮力等于物体重为,而在酒精中受到的浮力为,故在酒精中下沉,不能漂浮,故错; ,假设它在水和酒精中都处于沉入底部,全部排开液体的状态,则它受到的浮力分别是:,; ,而现在是,故错. 故选.
当题目中有多个问题相关联时,可以先假设其中一种情况成立,由此再利用所学知识进行推理,可得出另外的情况是否成立.
9. -------------------------------------------------------------------------------
【答案】根据阿基米德原理知道,水受到水的浮力等于排开水的重,若两水面相平,弹簧测力计示数会为零.现在弹簧测力计的示数不为0,袋内水没有全浸入,据此分析判断. 若袋内水面与袋外水面相平,则排开水的体积等于袋内水的体积,根据阿基米德原理,此时排开水的重力等于袋内水的重力,所以测力计的示数应为零.而题中测力计示数为7N,说明袋内水没有全浸入水中,袋内水面比袋外水面高. 故选A.
10. -------------------------------------------------------------------------------
【解答】解:设P浸入液体的深度为h,P的横截面积为S1;液面至a的深度为H,a的横截面积为S2; 绳子对a的拉力: T1=F浮-G1=ρgS1h-G1; 能拉开a需要的最小力: T2=F压+GA=ρgHS2+G2; 要让水能自动从管中流出,T1≥T2, 即:ρgS1h-G1≥ρgHS2+G2, ∴单独由浮筒P的质量很小、浮筒P的浮力足够大、盖子a比浮筒轻不能满足T1≥T2,故AC都错; ∵ρgS1h-G1≥ρgHS2+G2, ∴ρgS1h>ρgHS2, ∴S1h>HS2, ∵h<H, ∴S1>S2,故B正确,D错误. 故选B.
【分析】对浮筒P进行受力分析,受到水的浮力F浮、重力G1、绳子的拉力T1,F浮=T1+G1; 对盖子a进行受力分析,受到重力G2、水的压力F压、绳子的拉力T2,盖子受到的拉力T2=G2+F压; 要让水能自动从管中流出,T1≥T2,即:F浮-G1≥G2+F压,据此分析判断.
11. -------------------------------------------------------------------------------
12. -------------------------------------------------------------------------------
C
(1)小球A漂浮在甲溢水杯液体中,小球受到的浮力等于重力,据此判断小球A的质量; (2)小球B浸没在乙溢水杯液体中,ρ B大于ρ 2,小球A将下沉,受到的浮力小于重力,据此判断小球B的质量是不是30g;根据小球A与小球B体积之比是1:2;求出ρ 1与ρ 2的关系.
解:A,∵小球A漂浮在甲溢水杯液体中,小球受到的浮力等于重力,由F 浮=G 排=G A,可得小球A的质量为36g;故A错 B,小球A漂浮在甲溢水杯液体中,F 浮′=G 排′=m 排′g=ρ 1V 排g= ρ 1V Ag=36×10 -3kg×g, V A= ∵小球浸没在液体中,并下沉, ∴ρ B大于ρ 2, ∴F 浮=G 排=m 排g<G B=m Bg, ∴小球的B质量:m B>m 排=30g,故B错; C,小球B的体积: V B= = ∵V A:V B=1:2, 即: : = , ∴ρ 1:ρ 2=3:1.故C正确; D,A球质量就等于甲中溢出水的质量,而B球的质量未知所以无法求两球密度之比. 故选C.
13. -------------------------------------------------------------------------------
D
【分析】(1)四个相同的木块,密度相同,组合在一起时的密度仍与一个的相同,根据组合在一起时露出液面的高度为L/2,说明木块的密度小于水的密度,根据浮沉条件木块能漂浮在水面上。
(2)由组合成整体时露出液面的高度L/2可以计算得出水的密度与木块密度的关系。由这个密度关系可以得出分散之后各木块露出液面的高度。
【解答】由四个相同的木块组合在一起时处于漂浮状态可知木块的密度小于水的密度,所以当胶水溶于水木块分散后每块小木块由于密度小于水,也都将漂浮于水面。故A、B选项错误。 根据组合时露出水面的高度为L/2,可知露出液面的体积占组合木块总体的1/4,排开液体的体积是3/4。由于漂浮时浮力=重力,F=G总 , ρ水g(3/4)V木=ρ木gV木 , 所以(3/4)ρ水=ρ木。当木块分散后,由水和木块的密度关系可知,每个小木块都将有3/4的体积浸入水中,有1/4体积露出水面,由木块程立方体可知,将有1/4的高度露出水面,D选项正确。 故选D
14. -------------------------------------------------------------------------------
15. -------------------------------------------------------------------------------
【答案】因为ρ′>ρ,一开始小球将下沉,因为液体密度随深度而增大(ρ=ρ+kh),当液体的密度等于小球的密度时,小球将悬浮,据此求出h大小. 由题知,ρ′>ρ,一开始小球在液体中下沉,随着深度增加,液体的密度增加,当液体的密度等于小球的密度时,小球将悬浮, 设悬浮时的深度为h,则液体的密度ρ液=ρ+kh,则ρ′=ρ+kh,解得h=. 故选D.
16. -------------------------------------------------------------------------------
【答案】已知冰块与容器底部相接触并且相互间有压力,可以得出F浮=ρ水v排g<G冰,再根据冰化成水后质量(重力)不变,得出冰化成的水的体积与冰排开水的体积的关系,从而确定水面的升降.
∵冰熔化前,F浮+F支=G冰, ∴F浮=ρ水v排g<G冰,-------① 冰化水后,G冰=G水, 即:ρ冰v冰g=ρ水v水g,-------② 由①②可得: ρ水v排g<ρ水v水g, 即:冰熔化为水的体积大于排开水的体积, ∴冰熔化后,水面将上升. 故答案为:升高. 17. -------------------------------------------------------------------------------
;
18. -------------------------------------------------------------------------------
解:由“若把球放在盒内密封后,放入密度为ρ的液体中金属盒有h 1的高度露出液面,如图甲所示”可得ρL 2(L-h 1)=m 盒+m 球…①; 由乙图可得ρV 球+ρL 2(L-h 2)=m 盒+m 球…②; 由丙图可得ρL 2(L-h 3)=m 盒…③, 由①-③得m 球=ρL 2(h 3-h 1); 由①-②得V 球=L 2(h 2-h 1); 则金属球的密度ρ 球= = = ρ. 故答案为: ρ.
根据物体的浮沉条件分别列出甲,乙,丙三图的关系式,三式联立求得金属球的质量和体积表达式,再利用ρ= 即可求得金属球的密度.
19. -------------------------------------------------------------------------------
解:(1)∵铝槽漂浮, ∴铝槽受到的浮力: F浮=G=mg=0.54kg×10N/kg=5.4N; (2)由题知,铝槽排开水的体积: v排=sh=100×10-4m2×0.027m=2.7×10-4m3, ∵F浮=ρ液v排g, ∴液体的密度: ρ液===2×103kg/m3; (3)铝槽浸没时排开液体的体积: v排′=v铝===2×10-4m3, 液面上升的高度: h′===0.02m, 沉入前后液面变化值: △h=h-h′=0.027m-0.02m=0.007m 沉入前后液体对容器底的压强变化值: △p=ρ液g△h=2×103kg/m3×10N/kg×0.007m=140Pa. 故答案为:140.
(1)知道铝槽的质量,利用重力公式求铝槽重,又因为铝槽漂浮,利用漂浮条件求铝槽受到的浮力; (2)知道液面上升的高度,可求排开水的体积,利用阿基米德原理求液体的密度; (3)知道铝槽质量和密度,求铝的体积,也就知道铝槽浸没液体中排开液体的体积,又知道容器底面积,求液面上升的高度,和铝槽漂浮时上升的高度比较,利用液体压强公式求沉入前后液体对容器底的压强变化值.
20. -------------------------------------------------------------------------------
【解答】解:由甲、丙图可知,石块放在木块上时比木块多排开液体的体积: △V排=(h1-h3)S=(0.16m-0.1m)×50×10-4m2=3×10-4m3, 木块受到的浮力差: △F=ρ液g△V排=ρ液×10N/kg×3×10-4m3, ∵木块和石块放在木块上时的木块漂浮, ∴G石=ρ液×10N/kg×3×10-4m3; 由乙丙两图可知: 小石块的体积: V石=(h2-h3)S=(0.12m-0.1m)×50×10-4m2=1×10-4m3, 在图乙中,石块受到的浮力: F浮乙=ρ液gV石=ρ液×10N/kg×1×10-4m3, 小石块对杯底的压力: F=G-F浮乙=ρ液×10N/kg×3×10-4m3-ρ液×10N/kg×1×10-4m3=1.6N, 解得: ρ液=0.8×103kg/m3, 小石块的重力: G石=0.8×103kg/m3×10N/kg×3×10-4m3=2.4N, 小石块的质量:
m石==0.24kg, 小石块的密度: ρ石===2.4×103kg/m3. 故答案为:2.4×103kg/m3.
【分析】图甲比图丙多排开液体的体积是△V=(h1-h3)S,说明图甲中木块和小石块受到的总的浮力比图丙中木块受到的浮力要大:△F=ρ液g△V; 两次都是漂浮,总浮力都等于物体自身的重力,所以增大的浮力刚好等于小石块的重力; 图乙比图丙多排开液体的体积(h2-h3)S为小石块的体积, 在图乙中,小石块受到的浮力为F浮=ρ液gV石,小石块受到的重力与浮力之差就是石块对杯底的压力,据此求出液体的密度,求出小石块的质量,再利用密度公式求小石块的密度.
21. -------------------------------------------------------------------------------
【答案】(1)测量物体密度,一般应用的原理都是ρ=,如何得到鹅卵石的质量和体积是实验的关键. ①如图甲,在水盆内放入适量水,将塑料碗轻轻放入水中漂浮,用刻度尺测出此时水盆内水的深度为h1; 如图乙,将鹅卵石放在塑料碗中,装有鹅卵石的塑料碗仍在水中漂浮,用刻度尺测出此时水盆内水的深度为h2,设水盆的底面积为S,两次深度之差与底面积的乘积就是鹅卵石漂浮时排开水的体积;已知水的密度和鹅卵石漂浮时排开水的体积,可以得到鹅卵石漂浮排开水的质量,也就是鹅卵石的质量; ②如图丙,将塑料碗中的鹅卵石放入水盆中,用刻度尺测出此时水盆内水的深度为h3,h3与h1之差与水盆底面积的乘积就是鹅卵石浸没时排开水的体积,也就是鹅卵石的体积. (2)已知鹅卵石的质量和体积,利用ρ=,可得到其密度. 设水盆的底面积为S, 鹅卵石漂浮时排开水的体积V=(h2-h1)S, 鹅卵石漂浮时排开水的质量m=ρ水V=ρ水(h2-h1)S, 鹅卵石的质量m石=m=ρ水V=ρ水(h2-h1)S, 鹅卵石的体积V石=(h3-h1)S, 鹅卵石的密度ρ石===ρ水.
故答案为:ρ水.
22. -------------------------------------------------------------------------------
解:剪断细线,实心球下沉到容器底部时, 容器对桌面的压力增大值: △F 压=F 线=0.5N, 容器对桌面的压强增大值: △p= = =100Pa. 故答案为:100.
当剪断细线实心球下沉到容器底部时,对桌面的压力比只盛满液体对桌面的压力增大值为细线给球的拉力,再利用压强公式求出容器对桌面压强的增大值.
23. -------------------------------------------------------------------------------
【解答】解:密度计的重力不变,密度计处于漂浮状态,浮力等于重力,即浮力也不变. 设A、B、C三点显示的密度分别为ρ1、ρ2、ρ3; 则可得:ρ1gV1=ρ2gV2=ρ3gV3=G 约去g可得:ρ1V1=ρ2V2=ρ3V3=m V1-V2=-; V1-V3=-; 由题意知,V1-V2=s?AB,V1-V3=s?AC,又AB=2cm,AC=6cm. ∴3(V1-V2)=V1-V3; 即:3( -)=-; ∴3(-)=- 将ρ1及ρ2代入,可得: 3(-)=- 解得:ρ3=2×103kg/m3. 故答案为:2×103kg/m3.
【分析】因为已知密度计的测量范围,则可根据物体的浮沉条件得出液面在A和B点时密度计排开水的体积,则利用AC、CB两段的体积关系可得出液面在中点时的所测密度与液面分别在A、B两点时的密度关系,则可求得液面在C点时的所示密度.
24. -------------------------------------------------------------------------------
【答案】
木块密度为0.6×103kg/m3.
分别对木块所处的几种状态作出受力分析.
如图(a)(b)(c).
(a)(b)(c)
图(a)中,木块受拉力F1,重力和浮力.
图(b)中,细线剪断,木块处于漂浮状态,设排开水的体积为V排.
图(c)中,将露出水面的部分切去后,木块仍漂浮,这时再
施加F2=1 N的压力,仍有部分体积露出水面.
已知:F1=2N,F2=1N,V′=20cm3—2×10—5m3
求:水
解 根据三个图,木块均静止,分别列出受力平衡过程
将公式中各量展开,其中V排指图(b)中排开水的体积.
代入数值事理,过程中用国际单位(略)
水V—木V=
水V排—木V
(水V排—木V排)=+水×2×10—5
约去V排和V,求得:水=0.6×103kg/m3
25. -------------------------------------------------------------------------------
解:(1)圆柱体的重力:G=F=pS; (2)∵圆柱体漂浮 ∴F 浮=G ρ 水g V=ρ 0gV 则 = ; (3)∵圆柱体和塑料共同漂浮 ∴F 浮′=G ρ 水g(Sd+ V+Sh)=ρ 0gV+ρgSd ρ 水(Sd+ V+Sh)=ρ 水V+ρSd 则 = . 故答案为:(1)pS;(2) ;(3) .
(1)水平桌面上静止的物体,桌面受到的压力等于物体的重力,因此根据F=pS即可求出重力的大小; (2)根据物体漂浮时,浮力等于重力即可求出圆柱体和水的密度之比; (3)利用浮力等于重力即可求出塑料和水的密度之比.
26. -------------------------------------------------------------------------------
解:设木棒横截面积为s,小金属块在液体中受到的浮力为,
小金属块的受到重力:,
∵原来木棒漂浮在液体中,
∴,
即:ρ_,--------①
∵剪掉L'后,木棒悬浮在液体中,
∴'=G',
即:ρ_,--------②
由①-②得:
ρ_{2}(L-h)sg-ρ_{2}(L-L')sg=ρ_{1}Lsg-ρ_{1}(L-L')sg,
解得:L'=.
故答案为:
分两种状态分析:一、原来漂浮,根据漂浮条件列出受到浮力等于重力的关系式;二、剪掉L'后的悬浮,根据悬浮条件列出受到浮力等于重力的关系式;联立方程求解.
27. -------------------------------------------------------------------------------
【答案】根据密度公式ρ=进行分析,先根据放球前的水深18cm和放球后水深19.5cm以及容器的内部底面积求出球的体积;再根据碗漂浮时水面的高度、球和碗共同漂浮时水面的高度以及容器的底面积求出排开水的体积,然后结合阿基米德原理球的重力等于排开水的重力即可求出球的质量,知道金属球的质量和体积便可求出金属球的密度. 金属球的体积:V=Sh=400cm2×(19.5cm-18cm)=600cm3=6×10-4m3; 球和碗同时漂浮时,金属球排开水的体积V′=400cm2×(19.5cm+3cm-18cm)=18×10-4m3; 金属球的质量m=m排=ρ水V′=1.0×103kg/m3×18×10-4m3=1.8kg; 金属球的密度ρ===3×103kg/m3. 故答案为 3×103.
28. -------------------------------------------------------------------------------
【解答】解:①v物=80cm2×7.5cm=600cm3, 则物体A的高度为:hA===10cm; 因为物体在空气中静止时,绳子的拉力等于物体的重力即F1, 又因为F1与F2之差为7.2N, 因此物体在液体中受到的浮力等于7.2N; 即7.2N=ρ液gv物 7.2N=ρ液×10N/kg×600×10-6m3 ρ液=1.2×103kg/m3; ②如图乙,当物体A全部浸没在液体中时,以其底面所在平面为参考面,设其位置为e,那么在提出物体A时,在位置e以下的部分体积不再发生变化,因此不做考虑; 那么当物体A提起h2时,位置e以上的总体积保持不变,若设物体提起h2时,物体A在液面上的部分高度为xcm,那么以这个总体积不变作为等量关系,可列出: S容器?(hA+h1)=S物?x+S容器?(hA+h2-x),即: 80cm2×(10cm+3cm)=60cm2×x+80cm2×(10cm+5cm-x) 解得:x=8; 那么此时,物体A浸入液体中的高度为:h=10cm-8cm=2cm. ③已知:完全浸没时细绳对物体A的拉力为F2与提升高度h2时细绳对物体A的拉力为F3的比值为 5:8,得: (F1-F浮):(F1-ρ液gv排)=5:8,即: (ρ物gs物hA-ρ液gs物hA):(ρ物gs物hA-ρ液gs物h)=5:8 解得:ρ物=ρ液=×1.2×103kg/m3=2.8×103kg/m3; 故答案为:2.8×103.
【分析】先根据容器的底面积和上升的高度求出物体的体积,然后根据浮力的大小(F1与F2之差)求出液体的密度; 若求物体的密度,就必须利用“F2与F3之比为5:8”,物体全部浸没时,F2为F1与F浮的差,而将物体提升h2后,F3为F2与此时物体所受浮力的差,那么求出提升h2后,物体A排开液体的体积,即浸没在液体中部分的体积为解答此题的关键; 首先将研究对象简化,在图乙中,物体完全浸没时,以物体A的底面所在平面为参考面,在提升物体前后,此面以下的液体体积不会发生变化,所以可以先不予考虑;那么参考面以上部分,物体和液体的体积总和在提升物体前后始终不变,可利用这个等量关系来列出方程求得提升物体后,物体浸没在液体中的高度,进而可求出这部分的体积大小,即:排开液体的体积,由此整个题目的未知量全部求出.
29. -------------------------------------------------------------------------------
【解答】解:圆柱体A原来排开水的体积为V排,见图, 则V排=Sah′, 圆柱体A下降h后排开水的体积为V排′, 则V排′=Sa(h+h′+△h)=Sah′+Sa(h+△h), ∴排开水的体积的变化为:△V排=V排′-V排=Sah′+Sa(h+△h)-Sah′=Sa(h+△h), 两液面的变化为:△h==, 解得:△h=h, 则:△V排=Sb△h=h, 因此圆柱体A所受水的浮力增加为:△F浮=ρ水g△V排=ρ水gh. 故答案为:ρ水gh.
【分析】首先设圆柱体A原来浸在水中的深度为h′,放入圆柱体A后两液面的变化为△h,再利用公式V=Sh计算出圆柱体A原来排开水的体积和圆柱体A下降h后排开水的体积,从而可以计算出排开水的体积的变化,最后再利用公式F浮=ρ液V排g计算浮力的变化.
30. -------------------------------------------------------------------------------
【解答】解: ①把铁块和杯子看做一个整体,根据漂浮状态下F浮=G物,由于铁块和杯子的重力和始终不变,所以杯子和铁块受到总浮力不变; ②由阿基米德原理知,杯子和铁块受到的浮力为F浮=ρ液gV排,因为总F浮一直保持不变,且ρ液和g均不变,所以V排也不变,因此前后水面的高度h是不变的, 又因为P底=ρ液gh,ρ液gh始终不变,所以水对容器底的压强不变. 故答案为:不变;不变.
【分析】①漂浮的物体受到的浮力等于物体的重力.浮力是否变化根据重力是否变化判断; ②液体对容器底的压强用公式P=ρgh分析.
