2020中考数学专题4——几何模型之隐圆问题学案(含答案)
文档属性
| 名称 | 2020中考数学专题4——几何模型之隐圆问题学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 722.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 16:13:19 | ||
图片预览




文档简介
(
12
)
【模型讲解】
2020 中考专题 4——几何模型之隐圆问题
班级 姓名 .
常见的隐圆模型有:(1)动点到定点的距离为定长;(2)四点共圆;(3)定边对定角(专题 3)等.
AD=AC=AB ∠ADB=∠ACB 2∠ADB=∠ACB ∠BAC+∠BDC=180°
【例题分析】
例 1.如图,已知 AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD 的度数为 .
例 1 图 例 2 图 例 3 图
例 2.在矩形 ABCD 中,已知 AB ? 2cm , BC ? 3cm ,现有一根长为 2cm 的木棒 EF 紧贴着矩形的边
(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒 EF 的中点 P 在运动过程中所围成的图形的面积为 cm2 .
例 3.如图,定长弦 CD 在以 AB 为直径的⊙O 上滑动(点 C、D 与点 A、B 不重合),M 是 CD 的中
点,过点 C 作 CP⊥AB 于点 P,若 AB=8,则 PM 的最大值是 。
例 4.如图,点 A 与点 B 的坐标分别是(1,0),(5,0),点 P 是该直角坐标系内的一个动点.
使∠APB=30°的点 P 有 个;
若点 P 在 y 轴上,且∠APB=30°,求满足条件的点 P 的坐标;
当点 P 在 y 轴上移动时,∠APB 是否存在最大值?若存在,求点 P 的坐标;若不存在,请说明理由.
【巩固训练】
如图 1,矩形 ABCD 中, AB ? 2 , AD ? 3 ,点 E 、F 分别 AD 、DC 边上的点,且 EF ? 2 ,点G 为 EF 的中点,点 P 为 BC 上一动点,则 PA ? PG 的最小值为 .
图 1 图 2
如图 2,在矩形 ABCD 中, AB ? 4 , AD ? 6 , E 是 AB 边的中点, F 是线段 BC 边上的动点,将
?EBF 沿 EF 所在直线折叠得到△ EB?F ,连接 B?D ,则 B?D 的最小值是 .
在平面直角坐标系中,点 A 的坐标为(3, 0) ,点 B 为 y 轴正半轴上的一点,点C 是第一象限内一点,且 AC ? 2 .设tan ?BOC ? m ,则 m 的取值范围是 .
如图 3,在Rt?ABC 中, ?C ? 90? , AC ? 6 , BC ? 8 ,点 F 在边 AC 上,并且CF ? 2 ,点 E 为
边 BC 上的动点,将?CEF 沿直线 EF 翻折,点 C 落在点 P 处,则点 P 到边 AB 距离的最小值是 .
图 3 图 4 图 5
如图 4,四边形 ABCD 中, DC / / AB , BC ? 1 , AB ? AC ? AD ? 2 .则 BD 的长为 .
如图 5,在四边形 ABCD 中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,则∠BDC= ,
∠DBC= .
足球射门,不考虑其他因素,仅考虑射点到球门 AB 的张角大小时,张角越大,射门越好.如图 6 的正方形网格中,点 A,B,C,D,E 均在格点上,球员带球沿 CD 方向进攻,最好的射点在( )
点 C B.点 D 或点 E
C.线段 DE(异于端点)上一点 D.线段 CD(异于端点)上一点
图 6 图 7 图 8
如图 7,已知 AB 是⊙O 的直径,PQ 是⊙O 的弦,PQ 与 AB 不平行,R 是 PQ 的中点,作 PS⊥
PQ
AB,QT⊥AB,垂足分别为 S、T(S≠T),并且∠SRT=60°,则
的值等于 .
AB
如图 8,若 PA=PB,∠APB=2∠ACB,AC 与 PB 交于点 D,且 PB=4,PD=3,则 AD·DC= .
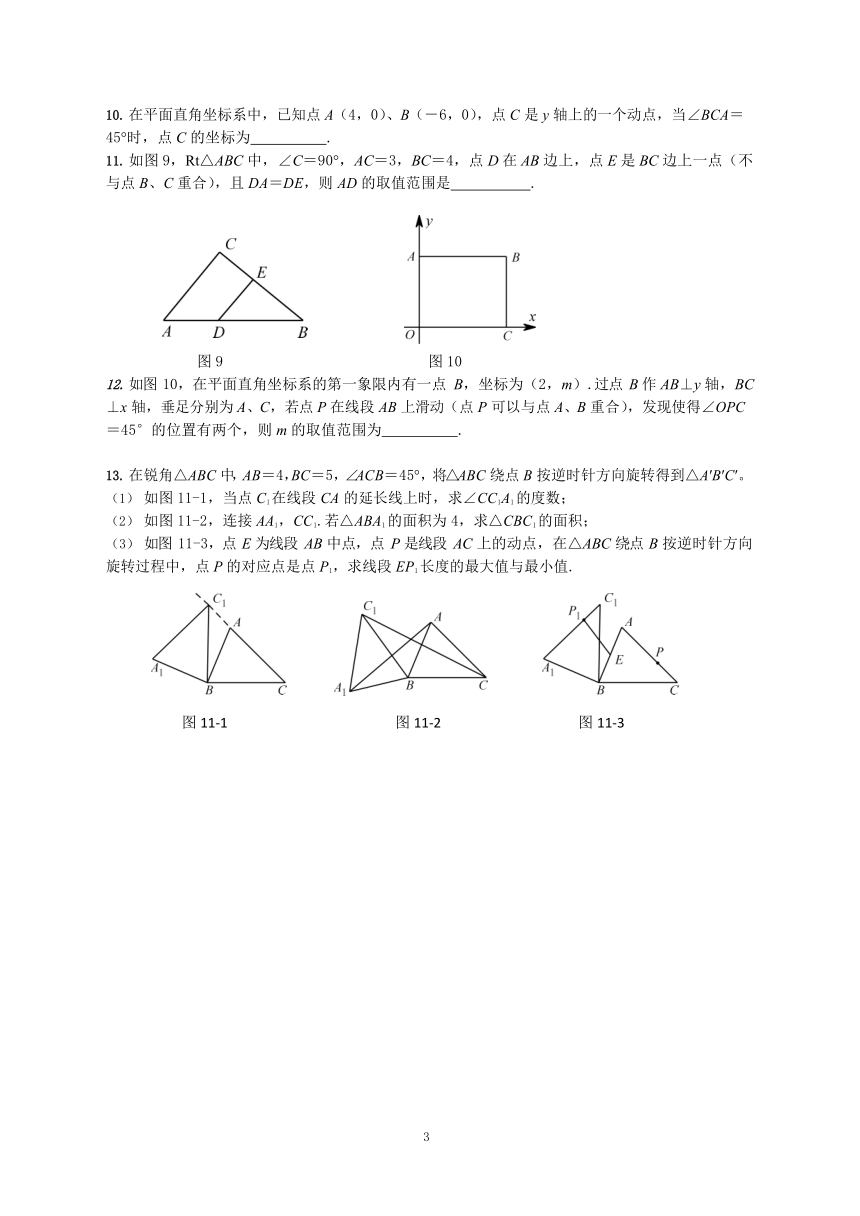
在平面直角坐标系中,已知点 A(4,0)、B(-6,0),点 C 是 y 轴上的一个动点,当∠BCA=
45°时,点 C 的坐标为 .
如图 9,Rt△ABC 中,∠C=90°,AC=3,BC=4,点 D 在 AB 边上,点 E 是 BC 边上一点(不与点 B、C 重合),且 DA=DE,则 AD 的取值范围是 .
图 9 图 10
如图 10,在平面直角坐标系的第一象限内有一点 B,坐标为(2,m).过点 B 作 AB⊥y 轴,BC
⊥x 轴,垂足分别为 A、C,若点 P 在线段 AB 上滑动(点 P 可以与点 A、B 重合),发现使得∠OPC
=45°的位置有两个,则 m 的取值范围为 .
在锐角△ABC 中,AB=4,BC=5,∠ACB=45°,将△ABC 绕点 B 按逆时针方向旋转得到△A′B′C′。
如图 11-1,当点 C1 在线段 CA 的延长线上时,求∠CC1A1 的度数;
如图 11-2,连接 AA1,CC1.若△ABA1 的面积为 4,求△CBC1 的面积;
如图 11-3,点 E 为线段 AB 中点,点 P 是线段 AC 上的动点,在△ABC 绕点 B 按逆时针方向旋转过程中,点 P 的对应点是点 P1,求线段 EP1 长度的最大值与最小值.
图 11-1 图 11-2 图 11-3
8
如图,抛物线 y=-
3
x2- 3
4
x+3 与 x 轴交于 A、B 两点(点 A 在点 B 的左侧),与 y 轴交于点
C. (1)求点 A、B 的坐标;
(2)若直线 l 过点 E(4,0),M 为直线 l 上的动点,当以 A、B、M 为顶点所作的直角三角形有且只有三个时,求直线 l 的解析式.
3
如图,直线 y=-
4
x+3 与 x 轴、y 轴分别交于 B、A 两点,点 P 是线段 OB 上的一动点,若能
在斜边 AB 上找到一点 C,使∠OCP=90°,设点 P 的坐标为(m,0),求 m 的取值范围.
2020 中考专题 4——几何模型之隐圆问题 参考答案
例 1.【解答】解:∵AB=AC=AD,
∴B,C,D 在以 A 为圆心,AB 为半径的圆上,
∴∠CAD=2∠CBD,∠BAC=2∠BDC,
∵∠CBD=2∠BDC,∠BAC=44°,
∴∠CAD=2∠BAC=88°. 故答案为:88°.
例 2【解答】解:如图所示:由题意根据直角三角形斜边上的中线等于斜边的一半,得出 P 到 B 点距离始终为 1,
则木棒 EF 的中点 P 在运动过程中的轨迹为分别以 A , B , C , D 为圆心,1cm 为半径的弧,
故所围成的图形的面积为:矩形面积?4 个扇形面积?
故答案为: 6 ??.
?? 2
(
90
1
2
)6 ? 4 ? ? 6 ??(cm ) .
360
例 3.【解答】解:连接 CO,MO,
∵∠CPO=∠CMO=90°,
∴C,M,O,P,四点共圆,且 CO 为直径(E 为圆心),
连接 PM,则 PM 为⊙E 的一条弦,当 PM 为直径时 PM 最大,所以
PM=CO=4 时 PM 最大.即 PMmax=4.
例 4【解答】解:(1)以 AB 为边,在第一象限内作等边三角形 ABC,以点 C 为圆心,AC 为半径作⊙C,交 y 轴于点 P1、P2.
在优弧 AP1B 上任取一点 P,如图 1,则∠APB=∠ACB= ×60°=30°.
∴使∠APB=30°的点 P 有无数个.故答案为:无数.
①当点 P 在 y 轴的正半轴上时, 过点 C 作 CG⊥AB,垂足为 G,如图 1.
∵点 A(1,0),点 B(5,0),∴OA=1,OB=5.
∴AB=4.
∵点 C 为圆心,CG⊥AB,∴AG=BG=AB=2.
∴OG=OA+AG=3.
∵△ABC 是等边三角形,∴AC=BC=AB=4.
∴CG= = =2 .
∴点 C 的坐标为(3,2).
过点 C 作 CD⊥y 轴,垂足为 D,连接 CP2,如图 1,
∵点 C 的坐标为(3,2),∴CD=3,OD=2.
∵P1、P2 是⊙C 与 y 轴的交点,∴∠AP1B=∠AP2B=30°.
∵CP2=CA=4,CD=3,∴DP2= = .
∵点 C 为圆心,CD⊥P1P2,∴P1D=P2D=.
∴P2(0,2﹣).P1(0,2+).
②当点 P 在 y 轴的负半轴上时,
同理可得:P3(0,﹣2﹣).P4(0,﹣2+).综上所述:满足条件的点 P 的坐标有:
(0,2﹣)、(0,2+)、(0,﹣2﹣)、(0,﹣2+).
当过点 A、B 的⊙E 与 y 轴相切于点 P 时,∠APB 最大.
理由:可证:∠APB=∠AEH,当∠APB 最大时,∠AEH 最大. 由 sin∠AEH= 得:当 AE
最小即 PE 最小时,∠AEH 最大.所以当圆与 y 轴相切时,∠APB 最大.
①当点 P 在 y 轴的正半轴上时,
连接 EA,作 EH⊥x 轴,垂足为 H,如图 2.
∵⊙E 与 y 轴相切于点 P,∴PE⊥OP.
∵EH⊥AB,OP⊥OH,∴∠EPO=∠POH=∠EHO=90°.
∴四边形 OPEH 是矩形.∴OP=EH,PE=OH=3.∴EA=3.
∵∠EHA=90°,AH=2,EA=3,
∴EH= = =
∴OP= ∴P(0,).
②当点 P 在 y 轴的负半轴上时, 同理可得:P(0,﹣).
理由:①若点 P 在 y 轴的正半轴上,
在 y 轴的正半轴上任取一点 M(不与点 P 重合),
连接 MA,MB,交⊙E 于点 N,连接 NA,如图 2 所示.
∵∠ANB 是△AMN 的外角,∴∠ANB>∠AMB.
∵∠APB=∠ANB,∴∠APB>∠AMB.
②若点 P 在 y 轴的负半轴上, 同理可证得:∠APB>∠AMB.
综上所述:当点 P 在 y 轴上移动时,∠APB 有最大值, 此时点 P 的坐标为(0,)和(0,﹣).
【巩固训练】答案
解:? EF ? 2 ,点G 为 EF 的中点,? DG ? 1 ,
? G 是以 D 为圆心,以 1 为半径的圆弧上的点,
作 A 关于 BC 的对称点 A? ,连接 A?D ,交 BC 于 P ,交以 D 为圆心,以1 为半径的圆于G ,此时 PA ? PG 的值最小,最小值为 A?G 的长;
? AB ? 2 , AD ? 3 ,? AA? ? 4 ,? A?D ? 5 ,
? A?G ? A?D ? DG ? 5 ? 1 ? 4 ;
? PA ? PG 的最小值为 4; 故答案为 4.
解:如图所示点 B? 在以 E 为圆心 EA 为半径的圆上运动,当 D 、 B? 、 E 共线时时,此时 B?D 的值最小,
根据折叠的性质, ?EBF ? △ EB?F ,
? EB? ? B?F ,
? EB? ? EB ,
? E 是 AB 边的中点, AB ? 4 ,
? AE ? EB? ? 2 ,
? AD ? 6 ,
(
6
2
?
2
2
) (
10
)? DE ? ? 2 ,
(
10
)? B?D ? 2 ? 2 .
解:C 在以 A 为圆心,以 2 为半径作圆周上,只有当OC 与圆 A 相切(即到C 点)时, ?BOC 最小,
(
5
)AC ? 2 , OA ? 3 ,由勾股定理得: OC ? ,
??BOA ? ?ACO ? 90? ,
??BOC ? ?AOC ? 90? , ?CAO ? ?AOC ? 90? ,
??BOC ? ?OAC ,
tan ?BOC ? tan ?OAC ? OC ? 5 ,
AC 2
随着C 的移动, ?BOC 越来越大,
? C 在第一象限,? C 不到 x 轴点,
即?BOC ? 90? ,?tan ?BOC
5 ,故答案为: m 5 .
2 2
解:如图所示:当 PE / / AB .
在Rt?ABC 中,? ?C ? 90? , AC ? 6 , BC ? 8 ,
(
6
2
?
8
2
)? AB ? ? 10 ,
由翻折的性质可知: PF ? FC ? 2 , ?FPE ? ?C ? 90? .
? PE / / AB ,
??PDB ? 90? .
由垂线段最短可知此时 FD 有最小值. 又? FP 为定值,
? PD 有最小值.
又??A ? ?A , ?ACB ? ?ADF ,
??AFD∽?ABC .
? AF ? DF , 即 4
? DF ,解得: DF ? 3.2 .
AB BC 10 8
? PD ? DF ? FP ? 3.2 ? 2 ? 1.2 .
解:以 A 为圆心,AB 长为半径作圆,延长 BA 交? A 于 F ,连接 DF .
? DC / / AB ,? D?F ? B?C ,? DF ? CB ? 1 , BF ? 2 ? 2 ? 4 ,
(
BF
2
?
DF
2
) (
15
)? FB 是? A 的直径,??FDB ? 90? ,? BD ? ? .
【解答】解:法一:∵AB=AC=AD,
∴∠ADB=∠ABD,∠ACB=∠ABC,∠ADC=∠ACD,
∵∠BAC=25°,∠CAD=75°,
∴∠ACB=(180°﹣25°)÷2=77.5°,∠DAB=∠DAC+∠CAB=100°,
∠ADC=∠ACD=(180°﹣75°)÷2=52.5°,
∴∠ADB=(180°﹣100°)÷2=40°,
∴∠BDC=∠ADC﹣∠ADB=52.5°﹣40°=12.5°,
∠DCB=∠DCA+∠ACB=52.5°+77.5°=130°,
∴∠DBC=180°﹣∠DCB﹣∠BDC=180°﹣130°﹣12.5°=37.5°.
∴∠BDC=12.5°,∠DBC=37.5°.
【解答】解:连接 BC,AC,BD,AD,AE,BE,
已知 A,B,D,E 四点共圆,同弧所对的圆周角相等,因而∠ADB=∠AEB,然后圆同弧对应的“圆内角“大于圆周角,“圆外角“小于圆周角,因而射门点在 DE 上时角最大,射门点在 D 点右上方或点 E 左下方时角度则会更小.
故选:C.
【解答】解:连结 OP,OQ,OR,如图,
∵R 是 PQ 的中点,∴OR⊥PQ,
∵OP=OQ,∴∠POR=∠QOR,
∵PS⊥AB,∴∠PSO=∠PRO=90°,
∴点 P、S、O、R 四点在以 OP 为直径的圆上,∴∠PSR=∠POR,
同理可得∠QTR=∠QOR,∴∠PSR=∠QTR,∴∠RST=∠RTS,而∠SRT=60°,
∴△RST 为等边三角形,∴∠RST=60°,∠RTS=60°,
∴∠RPO=∠RSO=60°,∠RQO=∠RTO=60°,∴△OPQ 为等边三角形,
∴PQ=OP,∴AB=2PQ,∴ = .故答案为 .
解析:本题主要考查三点共圆判定和相交弦定理。
由 PA=PB,∠APB=2∠ACB,可知:A,B,C 三点共圆,圆心为 P 半径为 PB。由相交弦定理可知:AD·DC=(PB+PD)(PB-PD)=7
【解答】解:设线段 BA 的中点为 E,
∵点 A(4,0)、B(﹣6,0),∴AB=10,E(﹣1,0).
如答图 1 所示,过点 E 在第二象限作 EP⊥BA,且 EP= AB=5,则易知△PBA 为等腰直
角三角形,∠BPA=90°,PA=PB= ;
以点 P 为圆心,PA(或 PB)长为半径作⊙P,与 y 轴的正半轴交于点 C,
∵∠BCA 为⊙P 的圆周角,∴∠BCA=∠BPA=45°,即则点 C 即为所求. 过点 P 作 PF⊥y 轴于点 F,则 OF=PE=5,PF=1,
在 Rt△PFC 中,PF=1,PC=,由勾股定理得:CF= =7,
∴OC=OF+CF=5+7=12,
∴点 C 坐标为(0,12);
如答图 2 所示,在第 3 象限可以参照(1)作同样操作,同理求得 y 轴负半轴上的点 C 坐标为(0,﹣12).
综上所述,点 C 坐标为(0,12)或(0,﹣12).故答案为:(0,12)或(0,﹣12).
【解答】解:∵Rt△ABC 中,∠C=90°,AC=3,BC=4,
∴AB= =5,以 D 为圆心,AD 的长为半径画⊙D,
①如图 1,当⊙D 与 BC 相切时,DE⊥BC 时,
设 AD=x,则 DE=AD=x,BD=AB﹣AD=5﹣x,
∵∠BED=∠C=90°,∠B 是公共角,
∴△BDE∽△BAC,∴ ,即 ,解得:x= ;
②如图 2,当⊙D 与 BC 相交时,若交点为 B 或 C,则 AD=AB= ,
∴AD 的取值范围是 ≤AD< .
【解答】解:
如图 3 中,在 x 轴上方作△OKC,使得△OKC 是以 OC 为斜边的等腰直角三角形,作 KE⊥AB
于 E.
∵OC=2,
∴OK=KC= ,
当 EK=KC= 时,以 K 为圆心,KC 为半径的圆与 AB 相切,此时 m
=BC=1+ ,在 AB 上只有一个点 P 满足∠OPC=∠OKC=45°, 当 BK= 时,在 AB 上恰好有两个点 P 满足∠OPC=∠OKC=45° 此时 m=BC=2,
综上所述,满足条件的 m 的值的范围为 2≤m<1+. 故答案为 2≤m<1+.
【解答】解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴ ,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,∴△ABA1∽△CBC1.
∴ ,
∵S△ABA1=4,∴S△CBC1= ;
①如图 1,过点 B 作 BD⊥AC,D 为垂足,
∵△ABC 为锐角三角形,∴点 D 在线段 AC 上, 在 Rt△BCD 中,BD=BC×sin45°=,
当 P 在 AC 上运动,BP 与 AC 垂直的时候,△ABC 绕点 B 旋转,使点 P 的对应点 P1 在线段 AB
上时,EP1 最小,最小值为:EP1=BP1﹣BE=BD﹣BE=﹣2;
②当 P 在 AC 上运动至点 C,△ABC 绕点 B 旋转,使点 P 的对应点 P1 在线段 AB 的延长线上时,
EP1 最大,最大值为:EP1=BC+BE=2+5=7.
14.【解答】解:(1)令 y=0,即 =0,
解得 x1=﹣4,x2=2,
∴A、B 点的坐标为 A(﹣4,0)、B(2,0).
抛物线 y=的对称轴是直线 x=﹣ =﹣1, 即 D 点的横坐标是﹣1,
S△ACB= AB?OC=9,
在 Rt△AOC 中,AC== =5,
设△ACD 中 AC 边上的高为 h,则有AC?h=9,解得 h=.
如答图 1,在坐标平面内作直线平行于 AC,且到 AC 的距离=h=,这样的直线有 2 条,分别是 l1 和 l2,则直线与对称轴 x=﹣1 的两个交点即为所求的点 D.
设 l1 交 y 轴于 E,过 C 作 CF⊥l1 于 F,则 CF=h=,
∴CE= = .
设直线 AC 的解析式为 y=kx+b,将 A(﹣4,0),C(0,3)坐标代入,得到 ,解得 ,
∴直线 AC 解析式为 y=x+3.
直线 l1 可以看做直线 AC 向下平移 CE 长度单位(个长度单位)而形成的,
∴直线 l1 的解析式为 y=x+3﹣ = x﹣ .
则 D1 的纵坐标为×(﹣1)﹣=,∴D1(﹣1,).
同理,直线 AC 向上平移个长度单位得到 l2,可求得 D2(﹣1,) 综上所述,D 点坐标为:D1(﹣1,),D2(﹣1,).
如答图 2,以 AB 为直径作⊙F,圆心为 F.过 E 点作⊙F 的切线,这样的切线有 2 条. 连接 FM,过 M 作 MN⊥x 轴于点 N.
∵A(﹣4,0),B(2,0),
∴F(﹣1,0),⊙F 半径 FM=FB=3.又∵E(4,0),
∴FE=5,
在 Rt△MEF 中,ME= =4,sin∠MFE= ,cos∠MFE= . 在 Rt△FMN 中 ,MN=MF?sin∠MFE=3× = , FN=MF?cos∠MFE=3× = ,则 ON=,
∴M 点坐标为(, )
直线 l 过 M(,),E(4,0),设直线 l 的解析式为 y=kx+b,则有
,解得 ,
所以直线 l 的解析式为 y=x+3.
同理,可以求得另一条切线的解析式为 y=x﹣3.
综上所述,直线 l 的解析式为 y=x+3 或 y=x﹣3.
15.【解题方法提示】令 y=0 求出点 B 的坐标,过点 C 作 CD⊥x 轴于 D,设点 C 的横坐标为 a, 则 OD=a,PD=m-a,求出△OCD 和△CPD 相似,利用相似三角形对应边成比例列式表示出 m,然后求出 m 的最小值;再根据点 P 在线段 OB 上判断出 OC⊥AB 时,点 P、B 重合,m 最大,然后即可写出 m 的取值范围.
m 的取值范围是 3≤m≤4.
同课章节目录
