2020中考数学专题5——几何模型之捆绑变换学案(含答案)
文档属性
| 名称 | 2020中考数学专题5——几何模型之捆绑变换学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 297.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 16:15:02 | ||
图片预览

文档简介
2020 中考数学专题 5——几何模型之捆绑变换
班级 姓名 .
【例题分析】
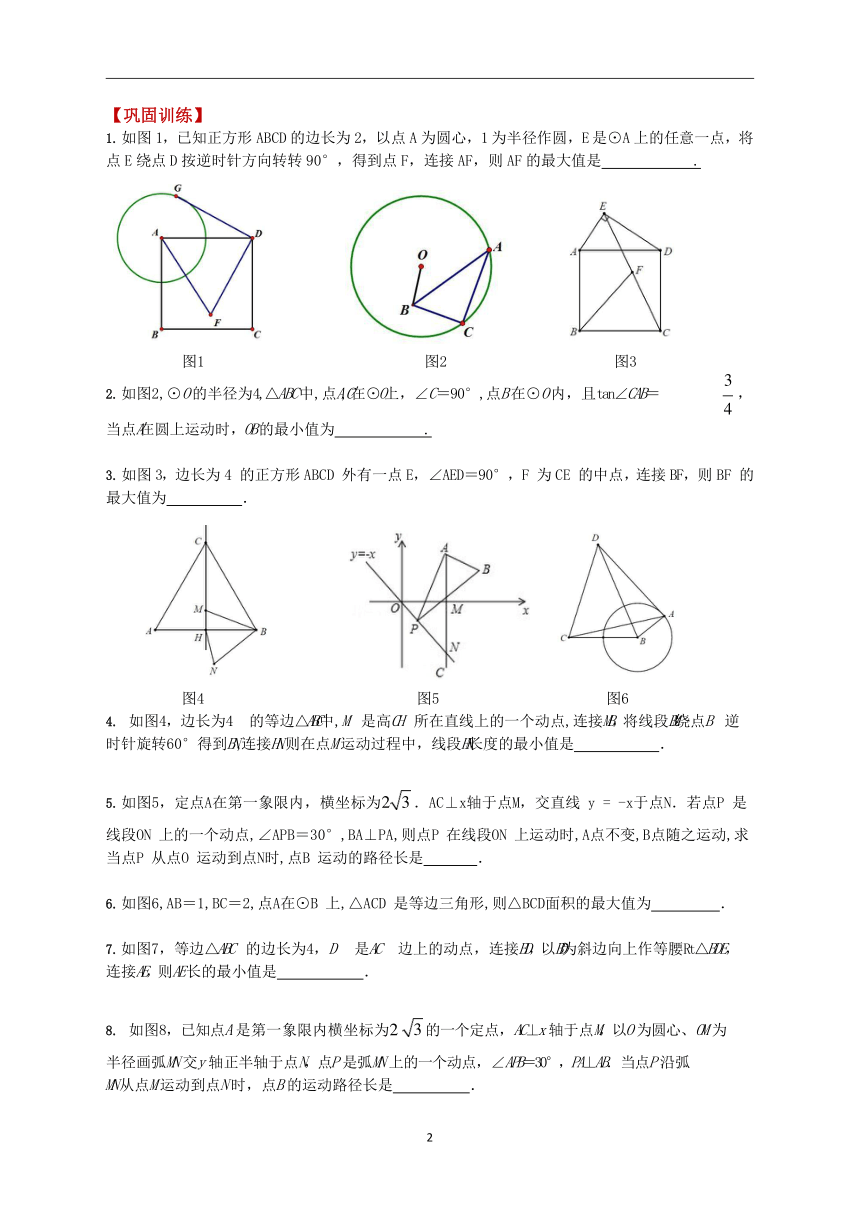
例 1. 如图 1,矩形 ABCD 中,AD=2AB=4,长度为 2 的动线段 AE 绕点 A 旋转,连接 EC,取 EC
的中点 F,连接 DF,求线段 DF 长的最大值和最小值.
图 1
例 2.如图 2,AB=4,O 为 AB 的中点,⊙O 的半径为 1.点 P 是⊙O 上一动点,以点 P 为直角顶点的等腰直角△PBC(点 P,B,C 按逆时针方向排列),则线段 AC 长的取值范围是 .
图 2
例 3.如图,点 O 为坐标原点,⊙O 的半径为 1,点 A(2,0).动点 B 在⊙O 上,连结 AB,作等边△ABC(A,B,C 为顺时针顺序),求 OC 的最大值与最小值.
(
4
)
【巩固训练】
如图 1,已知正方形 ABCD 的边长为 2,以点 A 为圆心,1 为半径作圆,E 是⊙A 上的任意一点,将点 E 绕点 D 按逆时针方向转转 90°,得到点 F,连接 AF,则 AF 的最大值是 .
图1 图2 图3
3
如图2,⊙O 的半径为4,△ABC 中,点A,C在⊙O上,∠C=90°,点B 在⊙O 内,且tan∠CAB= ,
4
当点A在圆上运动时,OB 的最小值为 .
如图 3,边长为 4 的正方形 ABCD 外有一点 E,∠AED=90°,F 为 CE 的中点,连接 BF,则 BF 的最大值为 .
图4 图5 图6
如图4,边长为4 的等边△ABC中,M 是高CH 所在直线上的一个动点,连接MB,将线段BM绕点B 逆时针旋转60°得到BN,连接HN.则在点M 运动过程中,线段HN长度的最小值是 .
(
3
)如图5,定点A在第一象限内,横坐标为2
.AC⊥x轴于点M,交直线 y = -x于点N.若点P 是
线段ON 上的一个动点,∠APB=30°,BA⊥PA,则点P 在线段ON 上运动时,A点不变,B点随之运动,求当点P 从点O 运动到点N时,点B 运动的路径长是 .
如图6,AB=1,BC=2,点A在⊙B 上,△ACD 是等边三角形,则△BCD面积的最大值为 .
如图7,等边△ABC 的边长为4,D 是AC 边上的动点,连接BD,以BD为斜边向上作等腰Rt△BDE, 连接AE,则AE 长的最小值是 .
(
3
)如图8,已知点A 是第一象限内横坐标为2
的一个定点,AC⊥x 轴于点M,以O 为圆心、OM 为
半径画弧MN 交y 轴正半轴于点N,点P 是弧MN 上的一个动点,∠APB=30°,PA⊥AB.当点P 沿弧
MN 从点M 运动到点N 时,点B 的运动路径长是 .
图7 图8 图9
9..如图9,已知以AB为直径的圆O, C为弧AB的中点,P为弧BC上任意一点,CD⊥CP交AP于D,连接BD,若AB=6.则BD的最小值为 。
10.如图 10,在平面直角坐标系中,点 A 的坐标为(2,0),点 B 的坐标为(5,0),点 P 为线段 AB外一动点,且 PA=2,PM=PB,∠BPM=90°。请直接写出线段 AM 长的最大值及此时点 P 的坐标。
2020 中考专题 5——几何模型之捆绑变换 参考答案
例 1.∵ O,F 分别是 AC,EC 的中点,∴OF 是ΔACE 的中位线,
(
5
)∴OF=(1/2)AE=1,∴点 F 在以 O 为圆心,1 为半径的圆上运动。易求得 OD=
(
5
) (
5
)∴DF 的最大值为 +1,最小值为 -1
例 2. 连接 O'C,连接 OP,易得
BO ? BP BO' BC
? ,且∠OBP=∠O'BC,所以ΔOBP∽ΔO'BC,所
(
1
)2
以 CO' ? CB ?
(
2
),所以 CO'=
(
2
),所以点 C 在以 O'为圆心,
(
2
)为半径的圆上运动。可求得
PO PB
AO'= 2 2 ,因此 AC 的最大值为2 2 + 2 =3 2 ,AC 的最小值为2 2 - 2 = 2 ,所以线段 AC 长
的取值范围是 2 ? AC ? 3 2 。
例 3.解:以 OA 为边向上作等边△OAO',连接 BO,CO', ∵△ABC 和△OAO'均为等边三角形 ∴A=AO',AB=AC,∠BAO=∠CAO' ∴△BAO≌△CAO',∴CO'=BO=1 ∴点 C 在以 O'为圆心,1 为半径的圆上运动. ∵OO'=AO=2,O'C=1,∴OC 的最大值为 3,最小值为 1. 【巩固训练】答案
1. 2 2 ?1; 2. 2; 3. 13 ?1 4.1 5. 2 2 6. 3 ?1 7. 2 8.π 9. 3 5 ? 3
10.AM 最大值为 2 2 ? 3 ,P 点坐标为( 2 - 2,2 )或( 2 - 2,- 2 )
同课章节目录
