2020中考数学专题6——几何模型之”12345学案(含答案)
文档属性
| 名称 | 2020中考数学专题6——几何模型之”12345学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 534.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 16:16:35 | ||
图片预览

文档简介
(
6
)
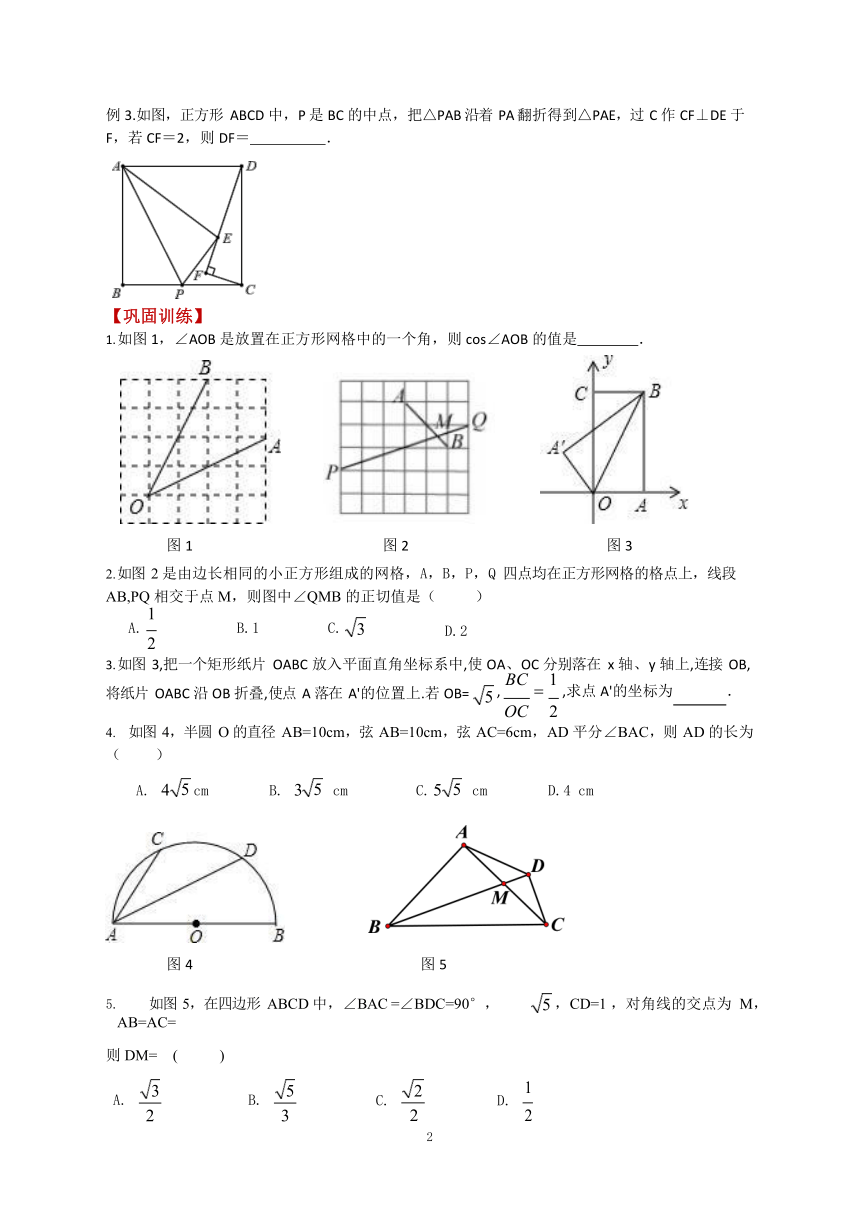
【模型解析】
2020 中考数学专题 6——几何模型之“12345”
班级 姓名 .
【例题分析】
例 1.在如图正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D 都在格点处,AB 与
CD 相交于 O,则 tan∠BOD 的值等于 。
例 1 图 例 2 图
k
例 2.(2017 浙江金华)如图,已知点 A(2,3)和点 B(0,2),点 A 在反比例函数 y=
x
的图象上.作射
线 AB,再将射线 AB 绕点 A 按逆时针方向旋转 45°,交反比例函数图象于点 C,则点 C 的坐标为 .
例 3.如图,正方形 ABCD 中,P 是 BC 的中点,把△PAB 沿着 PA 翻折得到△PAE,过 C 作 CF⊥DE 于
F,若 CF=2,则 DF= .
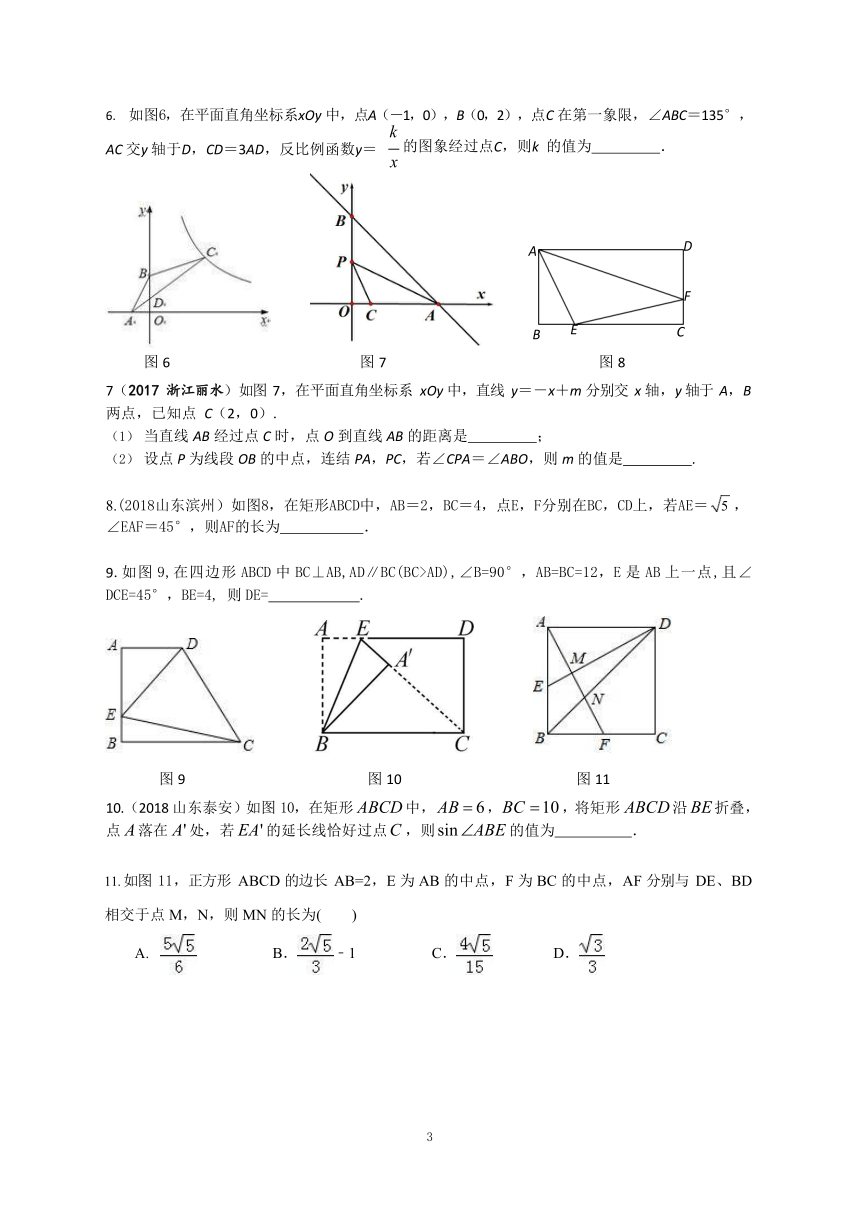
【巩固训练】
如图 1,∠AOB 是放置在正方形网格中的一个角,则 cos∠AOB 的值是 .
图 1 图 2 图 3
如图 2 是由边长相同的小正方形组成的网格,A,B,P,Q 四点均在正方形网格的格点上,线段
AB,PQ 相交于点 M,则图中∠QMB 的正切值是( )
(
3
)1
B.1 C.
2
D.2
如图 3,把一个矩形纸片 OABC 放入平面直角坐标系中,使 OA、OC 分别落在 x 轴、y 轴上,连接 OB,
将纸片 OABC 沿 OB 折叠,使点 A 落在 A'的位置上.若 OB=
, BC ? 1 ,求点 A'的坐标为 .
(
5
)OC 2
如图 4,半圆 O 的直径 AB=10cm,弦 AB=10cm,弦 AC=6cm,AD 平分∠BAC,则 AD 的长为
(
5
) (
5
) (
5
)( )
4
cm B. 3
cm C. 5
cm D.4 cm
图 4 图 5
(
5
)如图 5,在四边形 ABCD 中,∠BAC =∠BDC=90°,AB=AC=
则 DM= ( )
,CD=1 ,对角线的交点为 M,
(
3
) (
5
)B.
2 3
1
(
2
)C. D.
2 2
如图6,在平面直角坐标系xOy 中,点A(-1,0),B(0,2),点C 在第一象限,∠ABC=135°,
k
AC 交y 轴于D,CD=3AD,反比例函数y=
的图象经过点C,则k 的值为 .
x
D
F
E C
图 6 图 7 图 8
7(2017 浙江丽水)如图 7,在平面直角坐标系 xOy 中,直线 y=-x+m 分别交 x 轴,y 轴于 A,B
两点,已知点 C(2,0).
当直线 AB 经过点 C 时,点 O 到直线 AB 的距离是 ;
设点 P 为线段 OB 的中点,连结 PA,PC,若∠CPA=∠ABO,则 m 的值是 .
(
5
)8.(2018山东滨州)如图8,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若AE= ,
∠EAF=45°,则AF的长为 .
9.如图 9,在四边形 ABCD 中 BC⊥AB,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E 是 AB 上一点,且∠ DCE=45°,BE=4, 则 DE= .
图 9 图 10 图 11
10.(2018 山东泰安)如图 10,在矩形 ABCD 中, AB ? 6 ,BC ? 10 ,将矩形 ABCD 沿 BE 折叠, 点 A 落在 A' 处,若 EA' 的延长线恰好过点C ,则sin ?ABE 的值为 .
如图 11,正方形 ABCD 的边长 AB=2,E 为 AB 的中点,F 为 BC 的中点,AF 分别与 DE、BD
相交于点 M,N,则 MN 的长为( )
B. ﹣1 C. D.
如图 12,抛物线 y ? ?x2 ? bx ? c 与直线 y ? 1 x ? 2 交于 C、D 两点,其中点 C 在 y 轴上,
2
7
点 D 的坐标为(3,
2
F。
)。点 P 是 y 轴右侧的抛物线上一动点,过点 P 作 PE⊥x 轴于点 E,交 CD 于点
(1)求抛物线的解析式。 (2)若存在点 P,使∠PCF=45°,请直接写出相应的点 P 的坐标。
图 12
如图 13,抛物线 y=x2-4x+3 与坐标轴交于 A、B、C 三点,点 P 在抛物线上,PD⊥BC 于点 D, 垂足 D 在线段 BC 上.若 CD ? 1 ,求点 P 的坐标.
PD 2
图 13
2020 中考专题 6——几何模型之“12345” 参考答案
1
例 1.解:如图,∠BOD=∠OAD+∠OED,易得 tan∠OAD=
2
∠BOD=3.
1
,∠OED=45°,由“3”=“
2
”+45°得 tan
例2.解:如图,作AE⊥y轴于E,作AF⊥CF,垂足为F,且AF∥y轴.由点A(2,3)和点B(0,2),可得
1
BE=1.AE=2,所以tan∠BAE=
2
1
.因为∠BAC=45°,所以∠BAE+∠CAF=45°,由“
2
1
”+“
3
”=45°
1 CF 1
可得tan∠CAF= ,即 ? .设CF=a,则AF=3a,所以C点坐标可表示为(2-a,3-3a).把C(2-a,3-3a)
3 AF 3
代入 y ? 6 得(2-a)(3-3a)=6.解得a=3(a=0舍去).所以点C的坐标为(-1,-6).
x
1
例 3.解:因为在正方形 ABCD 中 P 是 BC 的中点,所以 tan∠BAP=
2
1
,由翻折可知∠EAP=∠BAP.由“ ”
2
1 4
+“ ”=“
2 3
4
”可知 tan∠BAE=
3
3
,所以 tan∠DAE=
4
,又因为 AE=AD,作 AH⊥DE,则∠DAH=∠EAH.
1 1
由“ ”+“
3 3
3
”=“
4
1
”可知 tan∠DAH=
3
1
,所以 tan∠CDF=
3
,所以 DF=3CF=6.
【巩固训练】答案
(
2
)1. 3 ; 2.D 3.( ? 3 , 4 ) 4.A 5.D 6. 9 7.(1) (2)12 8. 4 10
5 5 5 3
(
10
)1
9. 10.
3 10
11. C
12.(1) y ? ?x2 ? 7 x ? 2 (2)P( 1 , 7 )
2 2 2
简析:易得tan∠DCG= 1 ,因为∠PCF=45°,所以∠DCG+∠PCH=45°,由“ 1 ”+“ 1 ”=45°,
2 2 3
1 PH 1 7
可得tan∠PCH= .所以 ? ,设PH=a.则CH=3a.所以设 P(a,2+3a).所以? a2 ? a ? 2 ? 2 ? 3a ,
3 CH 3 2
所以 a ? 0(舍去)或a ? 1 .所以 P( 1 , 7 )。
2 2 2
13.P( 13 , 40 )
3 9
简析:易得 tan∠PCD=2,因为∠DCH=135°,所以 tan∠PCH=3.设 CH=a,则 PH=3a. 所以 P(3a,3+a)
代入抛物线解析式得9a2 ?12a ? 3 ? 3 ? a ,所以 a ? 0(舍去)或a ? 13 .所以 P( 13 , 40 )。
9 3 9
同课章节目录
