2020中考数学专题8——最值问题之将军饮马学案(含答案)
文档属性
| 名称 | 2020中考数学专题8——最值问题之将军饮马学案(含答案) | 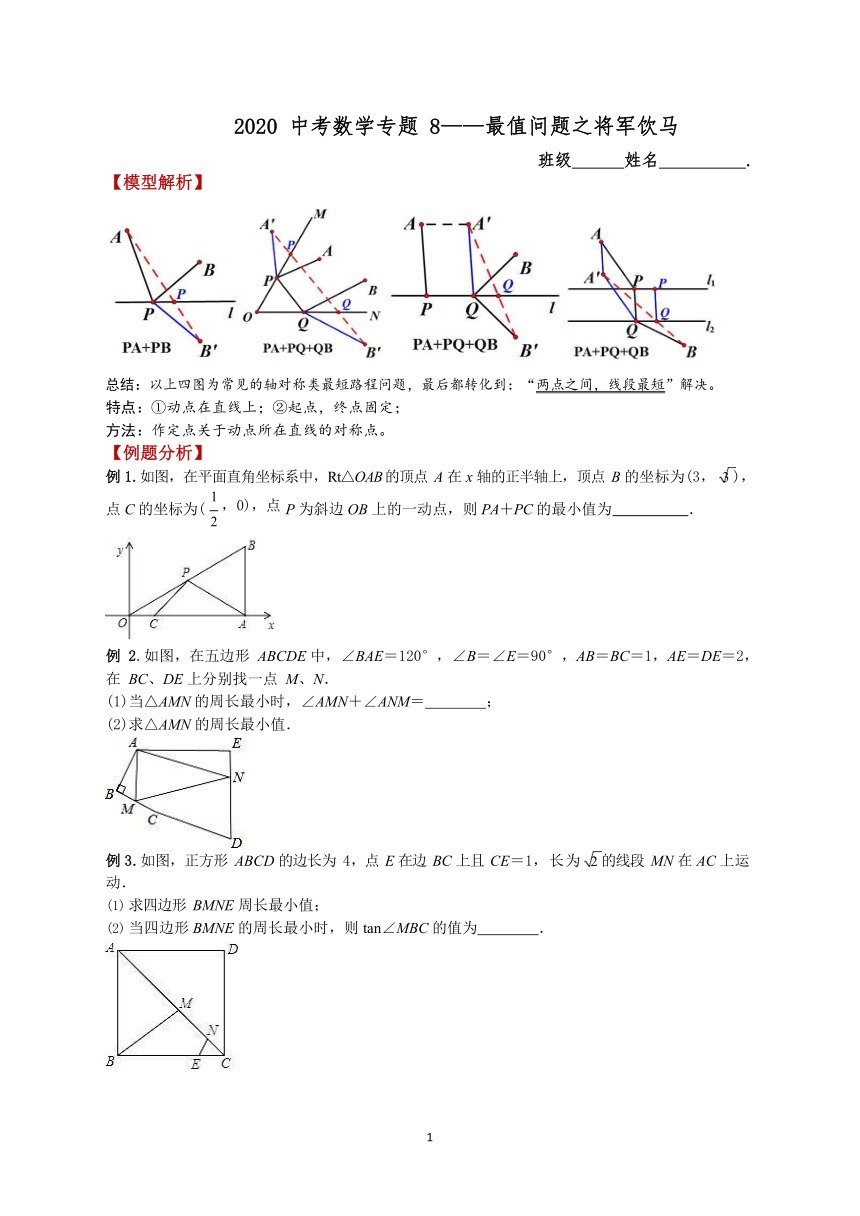 | |
| 格式 | zip | ||
| 文件大小 | 637.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 16:18:44 | ||
图片预览





文档简介
(
1
)
【模型解析】
2020 中考数学专题 8——最值问题之将军饮马
班级 姓名 .
总结:以上四图为常见的轴对称类最短路程问题,最后都转化到:“两点之间,线段最短”解决。 特点:①动点在直线上;②起点,终点固定;
方法:作定点关于动点所在直线的对称点。
【例题分析】
例 1.如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, 3 ),
点 C 的坐标为(
1 ,0),点
2
P 为斜边 OB 上的一动点,则 PA+PC 的最小值为 .
例 2.如图,在五边形 ABCDE 中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2, 在 BC、DE 上分别找一点 M、N.
(1)当△AMN 的周长最小时,∠AMN+∠ANM= ; (2)求△AMN 的周长最小值.
例 3.如图,正方形 ABCD 的边长为 4,点 E 在边 BC 上且 CE=1,长为 2 的线段 MN 在 AC 上运动.
求四边形 BMNE 周长最小值;
当四边形 BMNE 的周长最小时,则 tan∠MBC 的值为 .
例 4.在平面直角坐标系中,已知点 A(一 2,0),点 B(0,4),点 E 在 OB 上,且∠OAE=∠OBA.如图,将△AEO 沿 x 轴向右平移得到△AE′O′,连接 A'B、BE'.当 AB+BE'取得最小值时,求点 E'的坐标.
例 5.如图,已知正比例函数 y=kx(k>0)的图像与 x 轴相交所成的锐角为 70°,定点 A 的坐标为(0, 4),P 为 y 轴上的一个动点,M、N 为函数 y=kx(k>0)的图像上的两个动点,则 AM+MP+PN 的最小值为 .
【巩固训练】
如图 1 所示,正方形 ABCD 的面积为 12,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为 .
图 1 图 2 图 3 图 4
如图 2,在菱形 ABCD 中,对角线 AC=6,BD=8,点 E、F、P 分别是边 AB、BC、AC 上的动点,PE+PF 的最小值是 .
如图 3,在边长为 2 的等边△ABC 中,D 为 BC 的中点,E 是 AC 边上一点,则 BE+DE 的最小值为 .
如图 4,钝角三角形 ABC 的面积为 9,最长边 AB=6,BD 平分∠ABC,点 M、N 分别是 BD、BC
上的动点,则 CM+MN 的最小值为 .
如图 5,在△ABC 中,AM 平分∠BAC,点 D、E 分别为 AM、AB 上的动点, (1)若 AC=4,S△ABC=6,则 BD+DE 的最小值为
若∠BAC=30°,AB=8,则 BD+DE 的最小值为 .
若 AB=17,BC=10,CA=21,则 BD+DE 的最小值为 .
(
[
南瓜讲数学
]
系列之中考专题
)
(
2
) (
图
5
)
(
3
)如图 6,在△ABC 中,AB=BC=4,S△ABC=4一点,则 PK+QK 的最小值为 .
,点 P、Q、K 分别为线段 AB、BC、AC 上任意
(
[
南瓜讲数学
]
系列之中考专题
)
(
3
)
图 6 图 7 图 8 图 9
如图 7,AB 是⊙O 的直径,AB=8,点 M 在⊙O 上,∠MAB=20°,N 是弧 MB 的中点,P 是直径 AB 上的一动点,则 PM+PN 的最小值为 .
如图 8,在锐角△ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交 BC 于点 D,M、N 分别是
AD 和 AB 上的动点,则 BM+MN 的最小值是 .
如图 9,圆柱形玻璃杯高为 12cm、底面周长为 18cm,在杯内离杯底 4cm 的点 C 处有一滴蜂蜜, 此时一只蚂蚁正好在杯外壁,离杯上沿 4cm 与蜂蜜相对的点 A 处,则蚂蚁到达蜂蜜的最短距离为
(
3
) cm.
如图 10,菱形 OABC 中,点 A 在 x 轴上,顶点 C 的坐标为(1,
OC、OB 上,则 CE+DE+DB 的最小值是 .
),动点 D、E 分别在射线
图 10 图 11 图 12 图 13
如图 11,点 A(a,1)、B(-1,b)都在双曲线 y=- 3 (x<0)上,点 P、Q 分别是 x 轴、y 轴上
x
的动点,当四边形 PABQ 的周长取最小值时,PQ 所在直线的解析式是 .
如图 12,点 P 是∠AOB 内任意一点,OP=5cm,点 M 和点 N 分别是射线 OA 和射线 OB 上的动点,△PMN 周长的最小值是 5cm,则∠AOB 的度数是 .
如图 13,∠AOB=30°,点 M、N 分别在边 OA、OB 上,且 OM=1,ON=3,点 P、Q 分别在边 OB、OA 上,则 MP+PQ+QN 的最小值是 .
如图 14,在 Rt△ABC 中,∠ACB=90°,点 D 是 AB 边的中点,过 D 作 DE⊥BC 于点 E. (1)点 P 是边 BC 上的一个动点,在线段 BC 上找一点 P,使得 AP+PD 最小,在下图中画出点 P; (2)在(1)的条件下,连接 CD 交 AP 于点 Q,求 AQ 与 PQ 的数量关系;
图 14
在矩形 ABCD 中,AB=6,BC=8,G 为边 AD 的中点.
如图 1,若 E 为 AB 上的一个动点,当△CGE 的周长最小时,求 AE 的长.
如图 2,若 E、F 为边 AB 上的两个动点,且 EF=4,当四边形 CGEF 的周长最小时,求 AF
的长.
如图,抛物线 y ? ? 1 x2 ? 2x ? 4 交y 轴于点B,点A 为x 轴上的一点,OA=2,过点A 作直线MN ? AB
2
交抛物线与 M、N 两点.
求直线 AB 的解析式;
将线段 AB 沿 y 轴负方向平移 t 个单位长度,得到线段 A1B1 ,求 MA1 ? MB1 取最小值时实数 t
的值.
2020 中考专题 8——最值问题之将军饮马 参考答案
(
3
) (
3
)例 1.解:作 A 关于 OB 的对称点 D,连接 CD 交 OB 于 P,连接 AP,过 D 作 DN⊥OA 于 N, 则此时 PA+PC 的值最小,
∵DP=PA,∴PA+PC=PD+PC=CD,∵B(3,
),∴AB=
,OA=3,
(
3
)∵tan∠AOB= AB = 3 ,∴∠AOB=30°,∴OB=2AB=2 ,
OA 3
1 1 3 3
由三角形面积公式得:
×OA×AB=
2
×OB×AM,∴AM=
2
,∴AD=2×
2
=3,
2
∵∠AMB=90°,∠B=60°,∴∠BAM=30°,∵∠BAO=90°,∴∠OAM=60°,
∵DN⊥OA,∴∠NDA=30°,∴AN= 1 AD=
2
3 ,由勾股定理得:
2
DN= 3 3 ,
2
∵C(
1 ,0),∴CN=3﹣ 1 ﹣
2 2
3 =1,在 Rt△DNC 中,由勾股定理得:DC= ,
(
31
)2 2
即 PA+PC 的最小值是 31 .
2
例 2.解:作 A 关于 BC 和 ED 的对称点 A′,A″,连接 A′A″,交 BC 于 M,交 ED 于 N,则 A′A″即为
△AMN 的周长最小值.
⑴作 EA 延长线的垂线,垂足为 H,∠BAE=120°,∴∠AA′A″+∠AA″A′=60°,
∠AA′A″=∠A′AM,∠AA″A′=∠EAN,∴∠CAN=120°-∠AA′A″-∠AA″A′=60°, 也就是说∠AMN+∠ANM=180°-60°=120°.
⑵过点 A′作 EA 延长线的垂线,垂足为 H,
(
3
)∵AB=BC=1,AE=DE=2,∴AA′=2BA=2,AA″=2AE=4, 则 Rt△A′HA 中,∵∠EAB=120°,∴∠HAA′=60°,
∵A′H⊥HA,∴∠AA″H=30°,∴AH= 1 AA′=1,∴A′H=
2
,A″H=1+4=5,
(
7
)∴A′A″=2 ,
(
2
)例 3.解:作 EF∥AC 且 EF= 于 P,
,连结 DF 交 AC 于 M,在 AC 上截取 MN=
,延长 DF 交 BC
(
2
)作 FQ⊥BC 于 Q,作出点 E 关于 AC 的对称点 E′,则 CE′=CE=1,将 MN 平移至 E′F′处,
则四边形 MNE′F′为平行四边形,
当 BM+EN=BM+FM=BF′时,四边形 BMNE 的周长最小, 由∠FEQ=∠ACB=45°,可求得 FQ=EQ=1,
∵∠DPC=∠FPQ,∠DCP=∠FQP,∴△PFQ∽△PDC,
∴ PQ
PQ ? QE ? EC
= PQ ,∴
CD
PQ PQ ? 2
1
= ,解得:PQ=
4
2 ,∴PC= 8 ,
3 3
由对称性可求得 tan∠MBC=tan∠PDC= 2 .
3
例 4.【提示】
将△AEO 向右平移转化为△AEO 不动,点 B 向左平移,则点 B 移动的轨迹为一平行于 x 轴的直线,所以作点 E 关于该直线的对称点 E1,连接 AE1,与该直线交点 F 即为最小时点 B 的位置,求出 BF长度即可求出点 E 向右平移的距离.
例 5.解:如图所示,直线 OC、y 轴关于直线 y=kx 对称,直线 OD、直线 y=kx 关于 y 轴对称,点
A′是点 A 关于直线 y=kx 的对称点.
作 A′E⊥OD 垂足为 E,交 y 轴于点 P,交直线 y=kx 于 M,作 PN⊥直线 y=kx 垂足为 N,
∵PN=PE,AM=A′M,∴AM+PM+PN=A′M+PM+PE=A′E 最小(垂线段最短), 在 RT△A′EO 中,∵∠A′EO=90°,OA′=4,∠A′OE=3∠AOM=60°,
(
4
2
?
2
2
) (
3
)∴OE= 1 OA′=2,A′E= =2 .
2
(
3
)∴AM+MP+PN 的最小值为 2 .
【巩固训练】答案
解:连接 BD,
∵点 B 与 D 关于 AC 对称,∴PD=PB,∴PD+PE=PB+PE=BE 最小.
(
3
)∵正方形 ABCD 的面积为 12,∴AB=2 又∵△ABE 是等边三角形,∴BE=AB=2
,
(
3
) (
3
),故所求最小值为 2 .
解:∵四边形 ABCD 是菱形,对角线 AC=6,BD=8,∴AB=5,
作 E 关于 AC 的对称点 E′,作 E′F⊥BC 于 F 交 AC 于 P,连接 PE,则 E′F 即为 PE+PF 的最
小值,∵ 1 ?AC?BD=AD?E′F,∴E′F= 24 ,∴PE+PF 的最小值为 24 .
2 5 5
解:作 B 关于 AC 的对称点 B′,连接 BB′、B′D,交 AC 于 E,此时 BE+ED=B′E+ED=B′D, 根据两点之间线段最短可知 B′D 就是 BE+ED 的最小值,
∵B、B′关于 AC 的对称,∴AC、BB′互相垂直平分,∴四边形 ABCB′是平行四边形,
(
3
) (
3
)∵三角形 ABC 是边长为 2,D 为 BC 的中点,∴AD⊥BC,AD= ,BD=CD=1,BB′=2AD=2 ,
(
3
)作 B′G⊥BC 的延长线于 G,∴B′G=AD= ,
(
7
)在 Rt△B′BG 中,BG=3,∴DG=BG﹣BD=3﹣1=2,在 Rt△B′DG 中,B′D= . 故 BE+ED 的最小值为 7 .
解:过点 C 作 CE⊥AB 于点 E,交 BD 于点 M,过点 M 作 MN⊥BC 于 N,
∵BD 平分∠ABC,ME⊥AB 于点 E,MN⊥BC 于 N,∴MN=ME,
∴CE=CM+ME=CM+MN 是最小值.
∵三角形 ABC 的面积为 9,AB 即 CM+MN 的最小值为 3.
=6,∴ 1
2
×6?CE=9,∴CE=3.
提示:作点 E 关于 AM 的对称点 E′,BH⊥AC 于 H,易知 BD+DE 的最小值即为 BH 的长. 答案:(1)3;(2)4;(3)8.
解:如图,过 A 作 AH⊥BC 交 CB 的延长线于 H,
(
3
) (
3
)∵AB=CB=4,S△ABC=4 ,∴AH=2 ,
∴cos∠HAB= AH = 2 3 = 3 ,∴∠HAB=30°,∴∠ABH=60°,∴∠ABC=120°,
AB 4 2
∵∠BAC=∠C=30°,
作点 P 关于直线 AC 的对称点 P′,过 P′作 P′Q⊥BC 于 Q 交 AC 于 K, 则 P′Q 的长度=PK+QK 的最小值,
∴∠P′AK=∠BAC=30°,∴∠HAP′=90°,∴∠H=∠HAP′=∠P′QH=90°,
(
3
)∴四边形 AP′QH 是矩形,∴P′Q=AH=2 ,
(
3
)即 PK+QK 的最小值为 2 .
解:作点 N 关于 AB 的对称点 N′,连接 OM、ON、ON′、MN′,
则 MN′与 AB 的交点即为 PM+PN 的最小时的点,PM+PN 的最小值=MN′,
∵∠MAB=20°,∴∠MOB=2∠MAB=2×20°=40°,
∵N 是弧 MB 的中点,∴∠BON= 1
2
∠MOB=
1 ×40°=20°,
2
由对称性,∠N′OB=∠BON=20°,∴∠MON′=∠MOB+∠N′OB=40°+20°=60°,
∴△MON′是等边三角形,∴MN′=OM=OB= 1 AB= 1 ? 8 =4,
2 2
∴PM+PN 的最小值为 4,
解:如图,作 BH⊥AC,垂足为 H,交 AD 于 M′点,过 M′点作 M′N′⊥AB,垂足为 N′,则 BM′+ M′N′为所求的最小值.
∵AD 是∠BAC 的平分线,∴M′H=M′N′,∴BH 是点 B 到直线 AC 的最短距离,
(
2
)∵AB=4,∠BAC=45°,∴BH=AB?sin45°=4× 2 =2 .
2
(
2
)∵BM+MN 的最小值是 BM′+M′N′=BM′+M′H=BH=2 .
解:沿过 A 的圆柱的高剪开,得出矩形 EFGH,
过 C 作 CQ⊥EF 于 Q,作 A 关于 EH 的对称点 A′,连接 A′C 交 EH 于 P,连接 AP, 则 AP+PC 就是蚂蚁到达蜂蜜的最短距离,
∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,
∵CQ=
1 ×18
2
cm=9cm,A′Q=12cm﹣4cm+4cm=12cm,
在 Rt△A′QC 中,由勾股定理得:A′C=15cm,故答案为:15.
解:连接 AC,作 B 关于直线 OC 的对称点 E′,连接 AE′,交 OC 于 D,交 OB 于 E,此时 CE+ DE+BD 的值最小,
∵四边形 OCBA 是菱形,∴AC⊥OB,AO=OC,即 A 和 C 关于 OB 对称,
∴CE=AE,∴DE+CE=DE+AE=AD,
∵B 和 E′关于 OC 对称,∴DE′=DB,∴CE+DE+DB=AD+DE′=AE′,
(
3
) (
3
)过 C 作 CN⊥OA 于 N,∵C(1, ),∴ON=1,CN= ,
由勾股定理得:OC=2,即 AB=BC=OA=OC=2,∴∠CON=60°,∴∠CBA=∠COA=60°,
∵四边形 COAB 是菱形,∴BC∥OA,∴∠DCB=∠COA=60°,
∵B 和 E′关于 OC 对称,∴∠BFC=90°,∴∠E′BC=90°﹣60°=30°,
(
3
)∴∠E′BA=60°+30°=90°,CF= 1 BC=1,由勾股定理得:BF=
2
=E′F,
在 Rt△EBA 中,由勾股定理得:AE′=4,即 CE+DE+DB 的最小值是 4.
11.解:把点 A(a,1)、B(﹣1,b)代入 y=﹣ 3 (x<0)得 a=﹣3,b=3,则 A(﹣3,1)、B (﹣1,
x
3),作 A 点关于 x 轴的对称点 C,B 点关于 y 轴的对称点 D,所以 C 点为(﹣3,﹣1),D 点为(1,
3),连结 CD 分别交 x 轴、y 轴于 P 点、Q 点,此时四边形 PABQ 的周长最小,
(
?
) (
?
)设直线 CD 的解析式为 y=kx+b,则??3k ? b ? ?1 ,解得?k ? 1 ,
所以直线 CD 的解析式为 y=x+2.
?k ? b ? 3
?b ? 2
12.解:分别作点 P 关于 OA、OB 的对称点 C、D,连接 CD,分别交 OA、OB 于点 M、N, 连接 OC、OD、PM、PN、MN,如图所示:
∵点 P 关于 OA 的对称点为 D,关于 OB 的对称点为 C,∴PM=DM,OP=OD,∠DOA=∠ POA;
∵点 P 关于 OB 的对称点为 C,∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=
1 ∠COD,
2
∵△PMN 周长的最小值是 5cm,∴PM+PN+MN=5,∴DM+CN+MN=5,即 CD=5=OP,
∴OC=OD=CD,即△OCD 是等边三角形,∴∠COD=60°,∴∠AOB=30°;
13 解:作 M 关于 OB 的对称点 M′,作 N 关于 OA 的对称点 N′, 连接 M′N′,即为 MP+PQ+QN 的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
(
10
) (
10
)∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°,
∴在 Rt△M′ON′中,M′N′=
.故答案为 .
解:(1)作点 A 关于 BC 的对称点 A′,连 DA′交 BC 于点 P.
(
3
)(2)由(1)可证得 PA 垂直平分 CD,∴AQ= CQ=3PQ
解:(1)∵E 为 AB 上的一个动点,
∴作 G 关于 AB 的对称点 M,连接 CM 交 AB 于 E,那么 E 满足使△CGE 的周长最小;
∵在矩形 ABCD 中,AB=6,BC=8,G 为边 AD 的中点,∴AG=AM=4,MD=12,
而 AE∥CD,∴△AEM∽△DCM,∴AE:CD=MA:MD,∴AE= CD ? MA =2;
MD
(2)∵E 为 AB 上的一个动点,
∴如图,作 G 关于 AB 的对称点 M,在 CD 上截取 CH=4,然后连接 HM 交 AB 于 E,接着在 EB 上截取 EF=4,那么 E、F 两点即可满足使四边形 CGEF 的周长最小.
∵在矩形 ABCD 中,AB=6,BC=8,G 为边 AD 的中点,
∴AG=AM=4,MD=12,而 CH=4,∴DH=2,
而 AE∥CD,∴△AEM∽△DHM,∴AE:HD=MA:MD,∴AE= HD ? MA
MD
= 2 ,
3
∴AF
=4+
2 = 14 .
3 3
16.解:(1)依题意,易得 B(0,4),A(2,0),则 AB 解析式: y ? ?2x ? 4
(2)∵AB⊥MN
∴直线 MN: y ? 1 x ? 1
2
? y ? ? 1 x2 ? 2x ? 4
?
与抛物线联立可得: ?
(
?
)? y ?
?
2
1 x ? 1
2
解得:M(-2,-2)
将 AB 向负方向平移 t 个单位后,A1(2,-t),B1(0,4-t)则 A1 关于直线 x=-2 的对称点 A2 为(-6,-t)
当 A2、M、B1 三点共线时, MA1 ? MB1 取最小值
∴ t ? 14
3
同课章节目录
