人教高中数学选修1-1 第二章2.1.1椭圆定义 课件(50张ppt)
文档属性
| 名称 | 人教高中数学选修1-1 第二章2.1.1椭圆定义 课件(50张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 12:58:42 | ||
图片预览









文档简介
(共52张PPT)
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
——仙女座星系
星系中的椭圆
——“传说中的”飞碟
动画演示:太阳系行星的运动
一、合作探究,形成概念:
1.取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个什么图形?笔尖(动点)满足什么几何条件?
2.如果把细绳的两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,画出的又是什么图形?这一过程中,笔尖(动点)满足什么几何条件?
请同学们用事先准备好的学习用具小组内共同完成一下任务,并思考相应问题。
思考
数学实验
(1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的
图形
1.在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
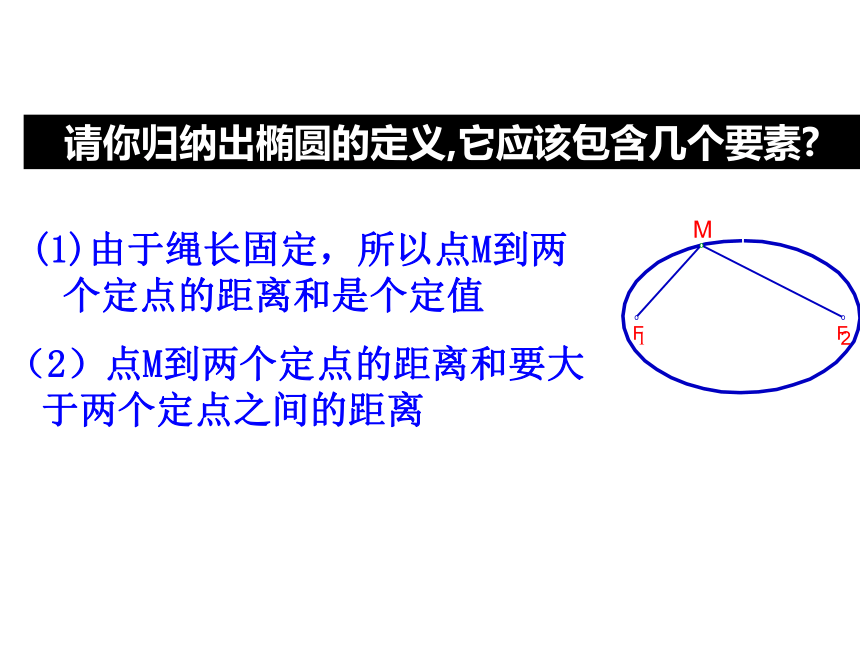
请你归纳出椭圆的定义,它应该包含几个要素
F
2
F
1
M
(1)由于绳长固定,所以点M到两个定点的距离和是个定值
(2)点M到两个定点的距离和要大
于两个定点之间的距离
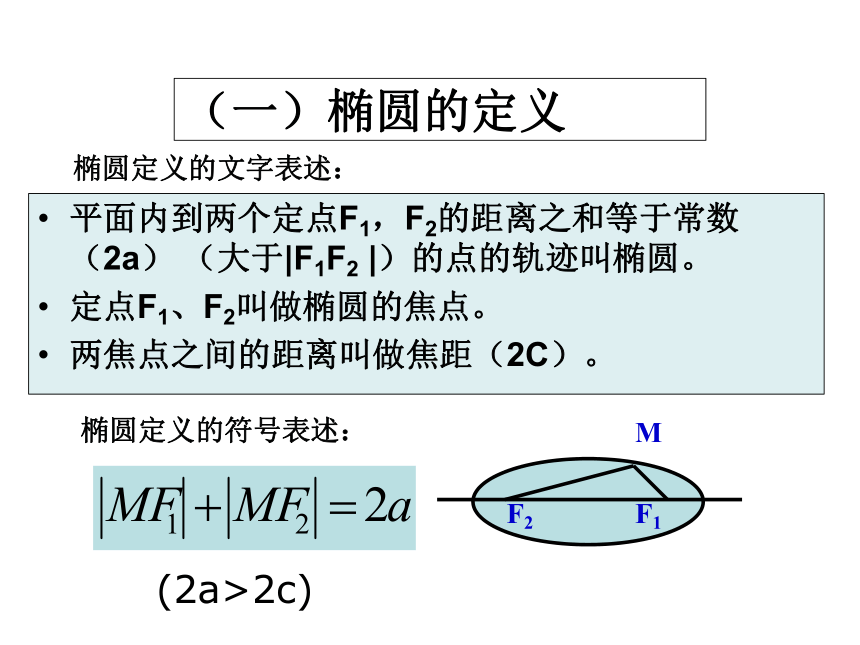
(一)椭圆的定义
平面内到两个定点F1,F2的距离之和等于常数
(2a)
(大于|F1F2
|)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2C)。
椭圆定义的文字表述:
椭圆定义的符号表述:
(2a>2c)
M
F2
F1
2a=2c
椭圆的定义
|
F1F2
|=2c
,
|
MF1
|+|M
F2
|=2a
2a<2c
结论:若常数大于|F1F2|,则点M的轨迹是(
)
若常数等于|F1F2|,则点M的轨迹是(
)
若常数小于|F1F2|,则点M的轨迹(
)
思考:当点M到F1、F2的距离之和不大于|F1F2|时,点M的轨迹是什么?
椭圆
线段F1F2
不存在
小结:椭圆的定义需要注意以下几点
1.平面上----这是大前提
2.动点M到两定点F1,F2的距离之和是常数2a
3.常数2a要大于焦距2C
探讨建立平面直角坐标系的方案
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(对称、“简洁”)
椭圆的方程的推导
建
设
现(限)
以经过椭圆焦点
F1,F2
的直线为
x
轴,线段F1F2的中垂线为y轴,建立直角坐标系xoy。
设
M(x,y)是椭圆上任一点,
设椭圆的焦距为
2c,点M与两焦点的距离之和为常数
2a。
故椭圆的两焦点坐标分别为
F1(-c,0)
和
F2(c,0)
由椭圆的定义得
(a
>
c)
2a
代
化
两边同时除以
,得
移项,得
平方化简,得
再平方化简,得
则方程可化为
观察左图,
和同桌讨论你们能从中找出表示c
、
a
的线段吗?
a2-c2
有什么几何意义?
由两点间的距离公式,可知:
设|F1F2|=2c(c>0),M(x,y)为椭圆上任意一点,则有F1(0,-c),F2(0,c),
又由椭圆
的定义可得:
|MF1|+
|MF2|=2a
(请大家比较一下上面两式的不同,独立思考后回答椭圆的标准方程。)
焦点在Y轴
焦点在X轴
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆
项分母较大.
焦点在y轴的椭圆
项分母较大.
椭圆方程有特点
系数为正加相连
分母较大焦点定
右边数“1”记心间
一、二、二、三
一个概念;
二个方程;
三个意识:求美意识,
求简意识,
猜想的意识。
二个方法:
去根号的方法;求标准方程的方法
|MF1|+|MF2|=2a
练习1:判定下列椭圆的焦点在哪个轴,并指
明a2、b2,写出焦点坐标
答:在
X
轴(-3,0)和(3,0)
答:在
y
轴(0,-5)和(0,5)
答:在y
轴。(0,-1)和(0,1)
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
1.口答:下列方程哪些表示椭圆?
若是,则判定其焦点在何轴?
并指明
,写出焦点坐标.
练习:
则a=
,b=
;
则a=
,b=
;
5
3
4
6
口答:
则a=
,b=
;
则a=
,b=
.
3
0练习:
a>3
练习:
1.方程4x2+ky2=1的曲线是焦点在y轴上的椭圆,则k的范围是
.
是
.
(0,4)
3.已知方程
表示焦点在x轴
上的椭圆,则m的取值范围是
.
变式:已知方程
表示焦点在y轴上的椭圆,则m的取值范
围是
.
(0,4)
(1,2)
2、
已知椭圆的方程为:
,请填空:
(1)
a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___.
变题:
若椭圆的方程为
,试口答完成(1).
若方程
表示焦点在y轴上的椭圆,
求k的取值范围;
探究:
若方程表示椭圆呢
5
4
3
6
(-3,0)、(3,0)
8
例1、填空:
(1)已知椭圆的方程为:
,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则 F2CD的周长为________
例题
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
|CF1|+|CF2|=2a
练习
1
椭圆 上一点P到一个焦点的距离为5,
则P到另一个焦点的距离为(
)
A.5
B.6
C.4
D.10
A
2.已知椭圆的方程为
,焦点在X轴上,
则其焦距为(
)
A
2
B
2
C
2
D
2
A
例2、写出适合下列条件的椭圆的标准方程
1
2
小结:先定位(焦点)再定量(a,b,c)
椭圆的焦点位置不能确定时,椭圆的标准方程一般有两种情形,必须分类求出
例1:平面内两个定点的距离是8,写出到这两个定点距离之和是10的动点的轨迹方程。
解:这个轨迹是一个椭圆。两个定点是焦点,用F1、F2表示,取过点F1、F2的直线为x轴,线段F1F2的垂直平分线为y
轴建立直角坐标系。
∵2a=10
2c=8
∴a=5
c=4
b2=a2 c2=9,
b=3
因此这个椭圆的标准方程是:
y
o
B
C
A
x
定义法求轨迹方程。
变题1:已知△ABC的一边BC固定,长为8,周长为18,求顶点A的轨迹方程。
.
解:以BC的中点为原点,BC所在的直线为x轴建立直角坐标系。
根据椭圆的定义知所求轨迹方程是椭圆,且焦点在轴上,所以可设椭圆的标准方程为
:
y
o
B
C
A
x
∵
2a=10,
2c=8
∴
a=5,
c=4
∴
b2=a2-c2=52-42=9
∴所求椭圆的标准方程为:
注意:求出曲线的方程后,要注意检查一下
方程的曲线上的点是否都是符合题意。
例1
已知椭圆的两个焦点坐标分别是(-2,0),
(2,0),
并且经过点
.求它的标准方程.
解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为
由椭圆的定义知
所以
又因为
,所以
因此,
所求椭圆的标准方程为
例题
演练
解法二:因为椭圆的焦点在x轴上,所以设它的标准方程为:
①
②
联立①②,
因此,
所求椭圆的标准方程为:
又∵焦点的坐标为
求椭圆标准方程的解题步骤:
(1)确定焦点的位置;
(2)设出椭圆系数法确定a、b的值,
写出椭圆的标准方程.
的标准方程;
(3)用待定
注意
:
求出曲线的方程后,要注意检查一下方程的曲线上的点是否都是符合题义。
例2、写出适合下列条件的椭圆的标准方程
(1)
a
=4,b=1,焦点在
x
轴上;
(2)
a
=4,b=1,焦点在坐标轴上;
(3)
两个焦点的坐标是(
0
,-2)和(
0
,2),并且经
过点P(
-1.5
,2.5).
解:
因为椭圆的焦点在y轴上,
设它的标准方程为
∵
c=2,且
c2=
a2
-
b2
∴
4=
a2
-
b2
……①
又∵椭圆经过点
∴
……②
联立①②可求得:
∴椭圆的标准方程为
(法一)
x
y
F1
F2
P
或
(法二)
因为椭圆的焦点在y轴上,所以设它的
标准方程为
由椭圆的定义知,
所以所求椭圆的标准方程为
练习:求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3),F2(0,3),且a=5.
答案:
(1)a=
,b=1,焦点在x轴上;
(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点;
(4)经过点P(-2,0)和Q(0,-3).
小结:求椭圆标准方程的步骤:
①定位:确定焦点所在的坐标轴;
②定量:求a,
b的值.
例1
:
已知一个运油车上的贮油罐横截面的外轮廓线是一
个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.
解:
以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y
轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为
根据题意有
即
因此,这个椭圆的标准方程为
x
y
O
F1
F2
3.
例题
回顾小结
求椭圆标准方程的方法
一种方法:
二类方程:
解:
例1
:将圆x2+y2
=
4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?
y
x
o
设所的曲线上任一点的坐标为(x,y),圆
=4上的对应点的坐标为(x’,y’),由题意可得:
因为 =4
所以
即
1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
练习
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。
(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹。
解
(1)因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。
(2)因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆(是线段F1F2)。
1、已知一个圆的圆心为坐标原点,半径为2,从这个圆上任意一点P向x轴作垂线段PP’,延长P’P至
M,使P’M=2
P’P,求点M的轨迹。
2、已知一个圆的圆心为坐标原点,半径为2,从这个圆上任意一点P向x轴作垂线段PP’。求线段PP’上使PM=2MP’的点M的轨迹。
3、已知一个圆的圆心为坐标原点,半径为2,从这个圆上任意一点P向y轴作垂线段PP’。
求PP’上PP’=-3P’M的点M的轨迹。
练习
例2
已知圆A:(x+3)2+y2=100,圆A内一
定点B(3,0),圆P过B点且与圆A内切,求圆心
P的轨迹方程.
解:设|PB|=r.
∵圆P与圆A内切,圆A的半径为10.
∴两圆的圆心距|PA|=10-r,
即|PA|+|PB|=10(大于|AB|).
∴点P的轨迹是以A、B两点为焦点的椭圆.
∴2a=10,
2c=|AB|=6,
∴a=5,c=3.
∴b2=a2-c2=25-9=16.
即点P的轨迹方程为
=1.
4、三角形ABC的三边a、b、c
成等差数列,
A、C的坐标分别为(-1,0),(1,0),
求顶点B的轨迹。
5、一动圆过点B(-3,0),
内切,求该动圆圆心M
的轨迹方程。
而且与圆
3
-3
x
y
M
A
B
C
8.在⊿ABC中,BC=24,AC、AB边上的中线之和为39,求⊿ABC的重心的轨迹方程.
y
x
o
E
F
G
A
C
B
x
y
O
P
F1
F2
练习
已知F1、F2是椭圆
的焦点,P为椭圆上
一点,且
,则
的面积为_____.
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
——仙女座星系
星系中的椭圆
——“传说中的”飞碟
动画演示:太阳系行星的运动
一、合作探究,形成概念:
1.取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个什么图形?笔尖(动点)满足什么几何条件?
2.如果把细绳的两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,画出的又是什么图形?这一过程中,笔尖(动点)满足什么几何条件?
请同学们用事先准备好的学习用具小组内共同完成一下任务,并思考相应问题。
思考
数学实验
(1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的
图形
1.在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
请你归纳出椭圆的定义,它应该包含几个要素
F
2
F
1
M
(1)由于绳长固定,所以点M到两个定点的距离和是个定值
(2)点M到两个定点的距离和要大
于两个定点之间的距离
(一)椭圆的定义
平面内到两个定点F1,F2的距离之和等于常数
(2a)
(大于|F1F2
|)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2C)。
椭圆定义的文字表述:
椭圆定义的符号表述:
(2a>2c)
M
F2
F1
2a=2c
椭圆的定义
|
F1F2
|=2c
,
|
MF1
|+|M
F2
|=2a
2a<2c
结论:若常数大于|F1F2|,则点M的轨迹是(
)
若常数等于|F1F2|,则点M的轨迹是(
)
若常数小于|F1F2|,则点M的轨迹(
)
思考:当点M到F1、F2的距离之和不大于|F1F2|时,点M的轨迹是什么?
椭圆
线段F1F2
不存在
小结:椭圆的定义需要注意以下几点
1.平面上----这是大前提
2.动点M到两定点F1,F2的距离之和是常数2a
3.常数2a要大于焦距2C
探讨建立平面直角坐标系的方案
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(对称、“简洁”)
椭圆的方程的推导
建
设
现(限)
以经过椭圆焦点
F1,F2
的直线为
x
轴,线段F1F2的中垂线为y轴,建立直角坐标系xoy。
设
M(x,y)是椭圆上任一点,
设椭圆的焦距为
2c,点M与两焦点的距离之和为常数
2a。
故椭圆的两焦点坐标分别为
F1(-c,0)
和
F2(c,0)
由椭圆的定义得
(a
>
c)
2a
代
化
两边同时除以
,得
移项,得
平方化简,得
再平方化简,得
则方程可化为
观察左图,
和同桌讨论你们能从中找出表示c
、
a
的线段吗?
a2-c2
有什么几何意义?
由两点间的距离公式,可知:
设|F1F2|=2c(c>0),M(x,y)为椭圆上任意一点,则有F1(0,-c),F2(0,c),
又由椭圆
的定义可得:
|MF1|+
|MF2|=2a
(请大家比较一下上面两式的不同,独立思考后回答椭圆的标准方程。)
焦点在Y轴
焦点在X轴
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆
项分母较大.
焦点在y轴的椭圆
项分母较大.
椭圆方程有特点
系数为正加相连
分母较大焦点定
右边数“1”记心间
一、二、二、三
一个概念;
二个方程;
三个意识:求美意识,
求简意识,
猜想的意识。
二个方法:
去根号的方法;求标准方程的方法
|MF1|+|MF2|=2a
练习1:判定下列椭圆的焦点在哪个轴,并指
明a2、b2,写出焦点坐标
答:在
X
轴(-3,0)和(3,0)
答:在
y
轴(0,-5)和(0,5)
答:在y
轴。(0,-1)和(0,1)
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
1.口答:下列方程哪些表示椭圆?
若是,则判定其焦点在何轴?
并指明
,写出焦点坐标.
练习:
则a=
,b=
;
则a=
,b=
;
5
3
4
6
口答:
则a=
,b=
;
则a=
,b=
.
3
0
a>3
练习:
1.方程4x2+ky2=1的曲线是焦点在y轴上的椭圆,则k的范围是
.
是
.
(0,4)
3.已知方程
表示焦点在x轴
上的椭圆,则m的取值范围是
.
变式:已知方程
表示焦点在y轴上的椭圆,则m的取值范
围是
.
(0,4)
(1,2)
2、
已知椭圆的方程为:
,请填空:
(1)
a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___.
变题:
若椭圆的方程为
,试口答完成(1).
若方程
表示焦点在y轴上的椭圆,
求k的取值范围;
探究:
若方程表示椭圆呢
5
4
3
6
(-3,0)、(3,0)
8
例1、填空:
(1)已知椭圆的方程为:
,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则 F2CD的周长为________
例题
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
|CF1|+|CF2|=2a
练习
1
椭圆 上一点P到一个焦点的距离为5,
则P到另一个焦点的距离为(
)
A.5
B.6
C.4
D.10
A
2.已知椭圆的方程为
,焦点在X轴上,
则其焦距为(
)
A
2
B
2
C
2
D
2
A
例2、写出适合下列条件的椭圆的标准方程
1
2
小结:先定位(焦点)再定量(a,b,c)
椭圆的焦点位置不能确定时,椭圆的标准方程一般有两种情形,必须分类求出
例1:平面内两个定点的距离是8,写出到这两个定点距离之和是10的动点的轨迹方程。
解:这个轨迹是一个椭圆。两个定点是焦点,用F1、F2表示,取过点F1、F2的直线为x轴,线段F1F2的垂直平分线为y
轴建立直角坐标系。
∵2a=10
2c=8
∴a=5
c=4
b2=a2 c2=9,
b=3
因此这个椭圆的标准方程是:
y
o
B
C
A
x
定义法求轨迹方程。
变题1:已知△ABC的一边BC固定,长为8,周长为18,求顶点A的轨迹方程。
.
解:以BC的中点为原点,BC所在的直线为x轴建立直角坐标系。
根据椭圆的定义知所求轨迹方程是椭圆,且焦点在轴上,所以可设椭圆的标准方程为
:
y
o
B
C
A
x
∵
2a=10,
2c=8
∴
a=5,
c=4
∴
b2=a2-c2=52-42=9
∴所求椭圆的标准方程为:
注意:求出曲线的方程后,要注意检查一下
方程的曲线上的点是否都是符合题意。
例1
已知椭圆的两个焦点坐标分别是(-2,0),
(2,0),
并且经过点
.求它的标准方程.
解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为
由椭圆的定义知
所以
又因为
,所以
因此,
所求椭圆的标准方程为
例题
演练
解法二:因为椭圆的焦点在x轴上,所以设它的标准方程为:
①
②
联立①②,
因此,
所求椭圆的标准方程为:
又∵焦点的坐标为
求椭圆标准方程的解题步骤:
(1)确定焦点的位置;
(2)设出椭圆系数法确定a、b的值,
写出椭圆的标准方程.
的标准方程;
(3)用待定
注意
:
求出曲线的方程后,要注意检查一下方程的曲线上的点是否都是符合题义。
例2、写出适合下列条件的椭圆的标准方程
(1)
a
=4,b=1,焦点在
x
轴上;
(2)
a
=4,b=1,焦点在坐标轴上;
(3)
两个焦点的坐标是(
0
,-2)和(
0
,2),并且经
过点P(
-1.5
,2.5).
解:
因为椭圆的焦点在y轴上,
设它的标准方程为
∵
c=2,且
c2=
a2
-
b2
∴
4=
a2
-
b2
……①
又∵椭圆经过点
∴
……②
联立①②可求得:
∴椭圆的标准方程为
(法一)
x
y
F1
F2
P
或
(法二)
因为椭圆的焦点在y轴上,所以设它的
标准方程为
由椭圆的定义知,
所以所求椭圆的标准方程为
练习:求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3),F2(0,3),且a=5.
答案:
(1)a=
,b=1,焦点在x轴上;
(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点;
(4)经过点P(-2,0)和Q(0,-3).
小结:求椭圆标准方程的步骤:
①定位:确定焦点所在的坐标轴;
②定量:求a,
b的值.
例1
:
已知一个运油车上的贮油罐横截面的外轮廓线是一
个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.
解:
以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y
轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为
根据题意有
即
因此,这个椭圆的标准方程为
x
y
O
F1
F2
3.
例题
回顾小结
求椭圆标准方程的方法
一种方法:
二类方程:
解:
例1
:将圆x2+y2
=
4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?
y
x
o
设所的曲线上任一点的坐标为(x,y),圆
=4上的对应点的坐标为(x’,y’),由题意可得:
因为 =4
所以
即
1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
练习
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。
(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹。
解
(1)因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。
(2)因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆(是线段F1F2)。
1、已知一个圆的圆心为坐标原点,半径为2,从这个圆上任意一点P向x轴作垂线段PP’,延长P’P至
M,使P’M=2
P’P,求点M的轨迹。
2、已知一个圆的圆心为坐标原点,半径为2,从这个圆上任意一点P向x轴作垂线段PP’。求线段PP’上使PM=2MP’的点M的轨迹。
3、已知一个圆的圆心为坐标原点,半径为2,从这个圆上任意一点P向y轴作垂线段PP’。
求PP’上PP’=-3P’M的点M的轨迹。
练习
例2
已知圆A:(x+3)2+y2=100,圆A内一
定点B(3,0),圆P过B点且与圆A内切,求圆心
P的轨迹方程.
解:设|PB|=r.
∵圆P与圆A内切,圆A的半径为10.
∴两圆的圆心距|PA|=10-r,
即|PA|+|PB|=10(大于|AB|).
∴点P的轨迹是以A、B两点为焦点的椭圆.
∴2a=10,
2c=|AB|=6,
∴a=5,c=3.
∴b2=a2-c2=25-9=16.
即点P的轨迹方程为
=1.
4、三角形ABC的三边a、b、c
成等差数列,
A、C的坐标分别为(-1,0),(1,0),
求顶点B的轨迹。
5、一动圆过点B(-3,0),
内切,求该动圆圆心M
的轨迹方程。
而且与圆
3
-3
x
y
M
A
B
C
8.在⊿ABC中,BC=24,AC、AB边上的中线之和为39,求⊿ABC的重心的轨迹方程.
y
x
o
E
F
G
A
C
B
x
y
O
P
F1
F2
练习
已知F1、F2是椭圆
的焦点,P为椭圆上
一点,且
,则
的面积为_____.
