华师大版数学九年级下册第27章 圆 测试卷(含答案)
文档属性
| 名称 | 华师大版数学九年级下册第27章 圆 测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 188.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 18:01:10 | ||
图片预览


文档简介
华师大版数学九年级下册第27章测试卷
一、选择题
1.已知⊙O的半径为5,点P到圆心O的距离为8,那么点P与⊙O的位置关系是( )
A.?点P在⊙O上?????????????????????? B.?点P在⊙O内?????????????????????
?C.?点P在⊙O 外?????????????????????? D.?无法确定
2.在平面直角坐标系中到原点的距离等于2的所有的点构成的图形是( )
A.?直线?????????????????????????????????????B.?正方形????????????????????????????????????C.?圆????????????????????????????????????D.?菱形
3.下面说法正确的是(?? ) 1)直径是弦;(2)弦是直径;(3)半圆是弧;(4)弧是半圆.
A.?(1)(2)??????????????????????B.?(2)(3)??????????????????????C.?(3)(4)??????????????????????D.?(1)(3)
4.如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为(?? )
A.?26°???????????????????????????????????????B.?52°???????????????????????????????????????C.?60°???????????????????????????????????????D.?64°
4题图 5题图
5. 小敏在作⊙O的内接正五边形时,先做了如下几个步骤: (i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1; (ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是(?? )
A.?BD2= OD?????????????B.?BD2= OD?????????????C.?BD2= OD?????????????D.?BD2= OD
6.如图,在△ABC中中,.⊙O截的三条边所得的弦长相等,则的度数为(? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
7.如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E . 若∠A=60°,BC=6,则图中阴影部分的面积为
A.?π??????????????????????????????????????B.?π??????????????????????????????????????C.?π??????????????????????????????????????D.?3π
6题图 7题图 8题图
8.如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于(?? )
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?55°???????????????????????????????????????D.?60°
9.如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
A.?20°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
9题图 10题图
10.如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B.C两点,PB=2㎝,BC=8㎝,则PA的长等于(??????? )
A.?4㎝???????????????????????????????????B.?16㎝???????????????????????????????????C.?20㎝???????????????????????????????????D.?2㎝
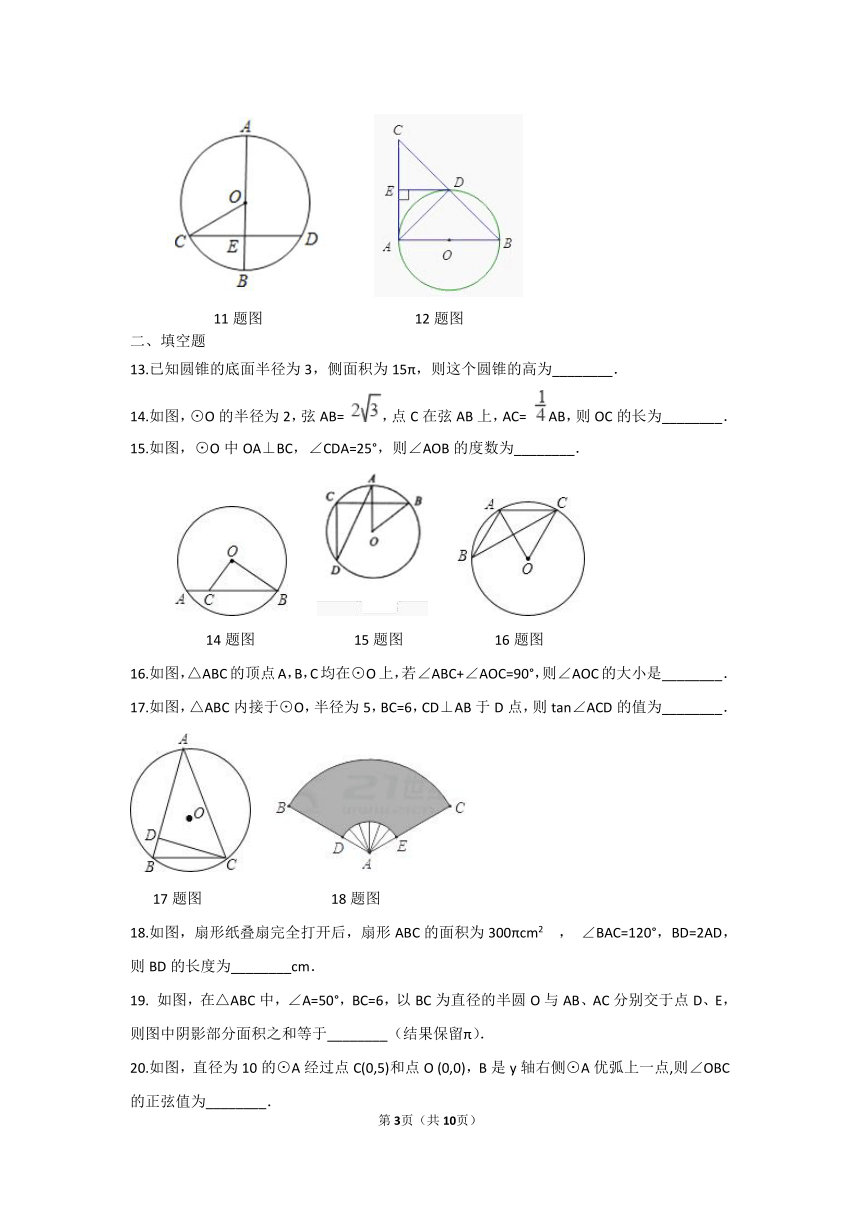
11.如图,已知⊙O的直径AB为10,弦CD=8,CD⊥AB于点E,则sin∠OCE的值为( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
12.如图所示,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线,正确的有(??)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11题图 12题图
二、填空题
13.已知圆锥的底面半径为3,侧面积为15π,则这个圆锥的高为________.
14.如图,⊙O的半径为2,弦AB= ,点C在弦AB上,AC= AB,则OC的长为________.
15.如图,⊙O中OA⊥BC,∠CDA=25°,则∠AOB的度数为________.
14题图 15题图 16题图
16.如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是________.
17.如图,△ABC内接于⊙O,半径为5,BC=6,CD⊥AB于D点,则tan∠ACD的值为________.
17题图 18题图
18.如图,扇形纸叠扇完全打开后,扇形ABC的面积为300πcm2 , ∠BAC=120°,BD=2AD,则BD的长度为________cm.
19. 如图,在△ABC中,∠A=50°,BC=6,以BC为直径的半圆O与AB、AC分别交于点D、E,则图中阴影部分面积之和等于________(结果保留π).
20.如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的正弦值为________.
19题图 20题图 21题图
21.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是________.
三、解答题
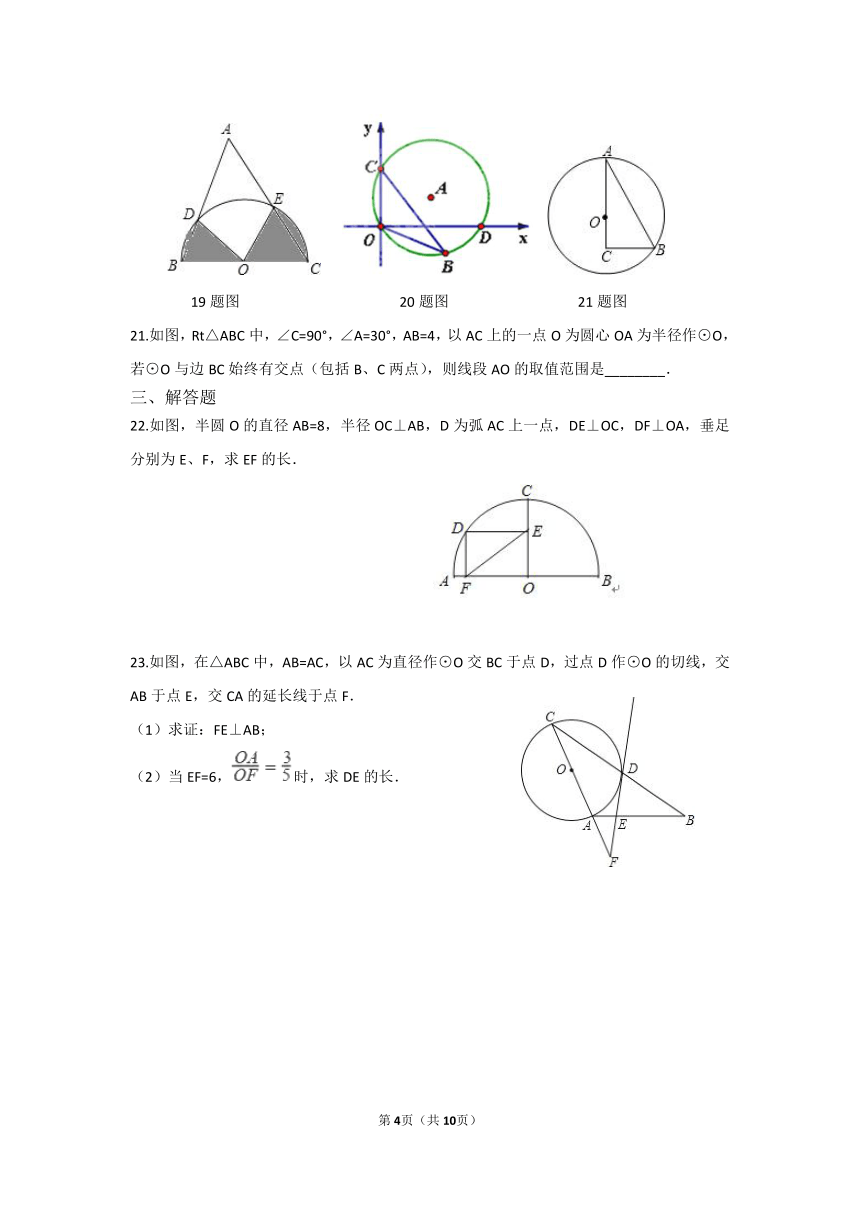
22.如图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长. ?
23.如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. (1)求证:FE⊥AB; (2)当EF=6,时,求DE的长.
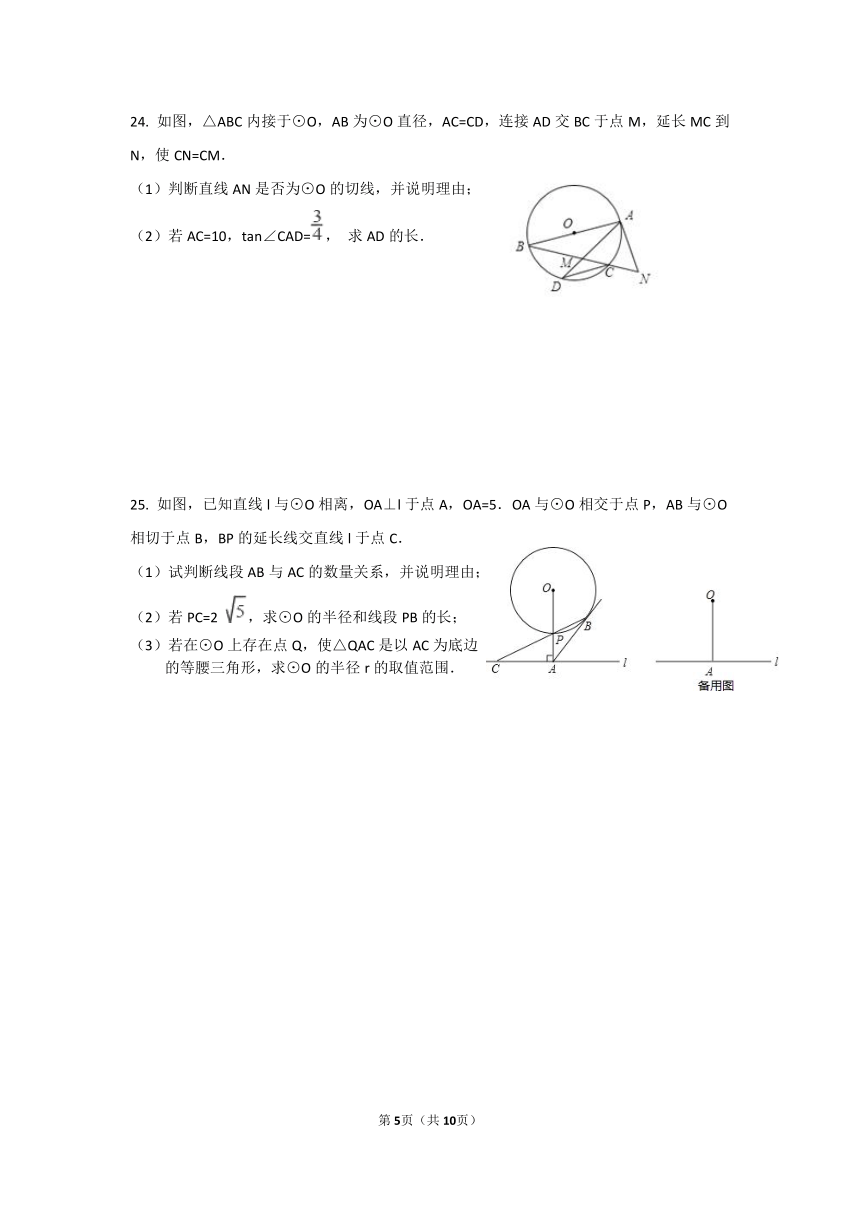
24. 如图,△ABC内接于⊙O,AB为⊙O直径,AC=CD,连接AD交BC于点M,延长MC到N,使CN=CM. (1)判断直线AN是否为⊙O的切线,并说明理由; (2)若AC=10,tan∠CAD=, 求AD的长.
25. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边
的等腰三角形,求⊙O的半径r的取值范围.
参考答案
一、选择题
C C D D C A D B B D B D
二、填空题
13. 4
14.
15. 50度
16. 60°
17.
18. 20
19. π
20.
21.
三、解答题
22. 解:连接OD. ∵OC⊥AB DE⊥OC,DF⊥OA, ∴∠AOC=∠DEO=∠DFO=90°, ∴四边形DEOF是矩形, ∴EF=OD. ∵OD=OA ∴EF=OA=4. ?
23. (1)证明:连接AD、OD, ∵AC为⊙O的直径, ∴∠ADC=90°, 又∵AB=AC, ∴CD=DB,又CO=AO, ∴OD∥AB, ∵FD是⊙O的切线, ∴OD⊥EF, ∴FE⊥AB; (2)∵, ∴, ∵OD∥AB, ∴,又EF=6, ∴DE=9. ?
24. 解:(1)直线AN是⊙O的切线,理由是: ∵AB为⊙O直径, ∴∠ACB=90°, ∴AC⊥BC, ∵CN=CM, ∴∠CAN=∠DAC, ∵AC=CD, ∴∠D=∠DAC, ∵∠B=∠D, ∴∠B=∠NAC, ∵∠B+∠BAC=90°, ∴∠NAC+∠BAC=90°, ∴OA⊥AN, 又∵点A在○O上, ∴直线AN是⊙O的切线; (2)过点C作CE⊥AD, ∵tan∠CAD=, ∴=, ∵AC=10, ∴设CE=3x,则AE=4x, 在Rt△ACE中,根据勾股定理,CE2+AE2=AC2 , ∴(3x)2+(4x)2=100, 解得x=2, ∴AE=8, ∵AC=CD, ∴AD=2AE=2×8=16.
25. (1)解:AB=AC,理由如下: 连接OB. ∵AB切⊙O于B,OA⊥AC, ∴∠OBA=∠OAC=90°, ∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°, ∵OP=OB, ∴∠OBP=∠OPB, ∵∠OPB=∠APC, ∴∠ACP=∠ABC, ∴AB=AC (2)解:延长AP交⊙O于D,连接BD, 设圆半径为r,则OP=OB=r,PA=5﹣r, 则AB2=OA2﹣OB2=52﹣r2 , AC2=PC2﹣PA2= ﹣(5﹣r)2 , ∴52﹣r2= ﹣(5﹣r)2 , 解得:r=3, ∴AB=AC=4, ∵PD是直径, ∴∠PBD=90°=∠PAC, 又∵∠DPB=∠CPA, ∴△DPB∽△CPA, ∴ = , ∴ = , 解得:PB= . ∴⊙O的半径为3,线段PB的长为 (3)解:作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出OE= AC= AB= 又∵圆O与直线MN有交点, ∴OE= ≤r, ≤2r, 25﹣r2≤4r2 , r2≥5, ∴r≥ , 又∵圆O与直线相离, ∴r<5, 即 ≤r<5
一、选择题
1.已知⊙O的半径为5,点P到圆心O的距离为8,那么点P与⊙O的位置关系是( )
A.?点P在⊙O上?????????????????????? B.?点P在⊙O内?????????????????????
?C.?点P在⊙O 外?????????????????????? D.?无法确定
2.在平面直角坐标系中到原点的距离等于2的所有的点构成的图形是( )
A.?直线?????????????????????????????????????B.?正方形????????????????????????????????????C.?圆????????????????????????????????????D.?菱形
3.下面说法正确的是(?? ) 1)直径是弦;(2)弦是直径;(3)半圆是弧;(4)弧是半圆.
A.?(1)(2)??????????????????????B.?(2)(3)??????????????????????C.?(3)(4)??????????????????????D.?(1)(3)
4.如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为(?? )
A.?26°???????????????????????????????????????B.?52°???????????????????????????????????????C.?60°???????????????????????????????????????D.?64°
4题图 5题图
5. 小敏在作⊙O的内接正五边形时,先做了如下几个步骤: (i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1; (ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是(?? )
A.?BD2= OD?????????????B.?BD2= OD?????????????C.?BD2= OD?????????????D.?BD2= OD
6.如图,在△ABC中中,.⊙O截的三条边所得的弦长相等,则的度数为(? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
7.如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E . 若∠A=60°,BC=6,则图中阴影部分的面积为
A.?π??????????????????????????????????????B.?π??????????????????????????????????????C.?π??????????????????????????????????????D.?3π
6题图 7题图 8题图
8.如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于(?? )
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?55°???????????????????????????????????????D.?60°
9.如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
A.?20°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
9题图 10题图
10.如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B.C两点,PB=2㎝,BC=8㎝,则PA的长等于(??????? )
A.?4㎝???????????????????????????????????B.?16㎝???????????????????????????????????C.?20㎝???????????????????????????????????D.?2㎝
11.如图,已知⊙O的直径AB为10,弦CD=8,CD⊥AB于点E,则sin∠OCE的值为( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
12.如图所示,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线,正确的有(??)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11题图 12题图
二、填空题
13.已知圆锥的底面半径为3,侧面积为15π,则这个圆锥的高为________.
14.如图,⊙O的半径为2,弦AB= ,点C在弦AB上,AC= AB,则OC的长为________.
15.如图,⊙O中OA⊥BC,∠CDA=25°,则∠AOB的度数为________.
14题图 15题图 16题图
16.如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是________.
17.如图,△ABC内接于⊙O,半径为5,BC=6,CD⊥AB于D点,则tan∠ACD的值为________.
17题图 18题图
18.如图,扇形纸叠扇完全打开后,扇形ABC的面积为300πcm2 , ∠BAC=120°,BD=2AD,则BD的长度为________cm.
19. 如图,在△ABC中,∠A=50°,BC=6,以BC为直径的半圆O与AB、AC分别交于点D、E,则图中阴影部分面积之和等于________(结果保留π).
20.如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的正弦值为________.
19题图 20题图 21题图
21.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是________.
三、解答题
22.如图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长. ?
23.如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. (1)求证:FE⊥AB; (2)当EF=6,时,求DE的长.
24. 如图,△ABC内接于⊙O,AB为⊙O直径,AC=CD,连接AD交BC于点M,延长MC到N,使CN=CM. (1)判断直线AN是否为⊙O的切线,并说明理由; (2)若AC=10,tan∠CAD=, 求AD的长.
25. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边
的等腰三角形,求⊙O的半径r的取值范围.
参考答案
一、选择题
C C D D C A D B B D B D
二、填空题
13. 4
14.
15. 50度
16. 60°
17.
18. 20
19. π
20.
21.
三、解答题
22. 解:连接OD. ∵OC⊥AB DE⊥OC,DF⊥OA, ∴∠AOC=∠DEO=∠DFO=90°, ∴四边形DEOF是矩形, ∴EF=OD. ∵OD=OA ∴EF=OA=4. ?
23. (1)证明:连接AD、OD, ∵AC为⊙O的直径, ∴∠ADC=90°, 又∵AB=AC, ∴CD=DB,又CO=AO, ∴OD∥AB, ∵FD是⊙O的切线, ∴OD⊥EF, ∴FE⊥AB; (2)∵, ∴, ∵OD∥AB, ∴,又EF=6, ∴DE=9. ?
24. 解:(1)直线AN是⊙O的切线,理由是: ∵AB为⊙O直径, ∴∠ACB=90°, ∴AC⊥BC, ∵CN=CM, ∴∠CAN=∠DAC, ∵AC=CD, ∴∠D=∠DAC, ∵∠B=∠D, ∴∠B=∠NAC, ∵∠B+∠BAC=90°, ∴∠NAC+∠BAC=90°, ∴OA⊥AN, 又∵点A在○O上, ∴直线AN是⊙O的切线; (2)过点C作CE⊥AD, ∵tan∠CAD=, ∴=, ∵AC=10, ∴设CE=3x,则AE=4x, 在Rt△ACE中,根据勾股定理,CE2+AE2=AC2 , ∴(3x)2+(4x)2=100, 解得x=2, ∴AE=8, ∵AC=CD, ∴AD=2AE=2×8=16.
25. (1)解:AB=AC,理由如下: 连接OB. ∵AB切⊙O于B,OA⊥AC, ∴∠OBA=∠OAC=90°, ∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°, ∵OP=OB, ∴∠OBP=∠OPB, ∵∠OPB=∠APC, ∴∠ACP=∠ABC, ∴AB=AC (2)解:延长AP交⊙O于D,连接BD, 设圆半径为r,则OP=OB=r,PA=5﹣r, 则AB2=OA2﹣OB2=52﹣r2 , AC2=PC2﹣PA2= ﹣(5﹣r)2 , ∴52﹣r2= ﹣(5﹣r)2 , 解得:r=3, ∴AB=AC=4, ∵PD是直径, ∴∠PBD=90°=∠PAC, 又∵∠DPB=∠CPA, ∴△DPB∽△CPA, ∴ = , ∴ = , 解得:PB= . ∴⊙O的半径为3,线段PB的长为 (3)解:作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出OE= AC= AB= 又∵圆O与直线MN有交点, ∴OE= ≤r, ≤2r, 25﹣r2≤4r2 , r2≥5, ∴r≥ , 又∵圆O与直线相离, ∴r<5, 即 ≤r<5
