北师大版九上数学第3章:3.2 用频率估计概率习题课件(22张)
文档属性
| 名称 | 北师大版九上数学第3章:3.2 用频率估计概率习题课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-25 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第2节 用频率估计概率
第三章 概率的进一步认识
北师版 九年级上
答案显示
习题链接
频率
0.90
D
B
A
2.4
D
D
p
答案显示
习题链接
1.求一个随机事件概率的基本方法可以是:通过大量的重复试验,用一个随机事件发生的________去估计它的概率.
概率
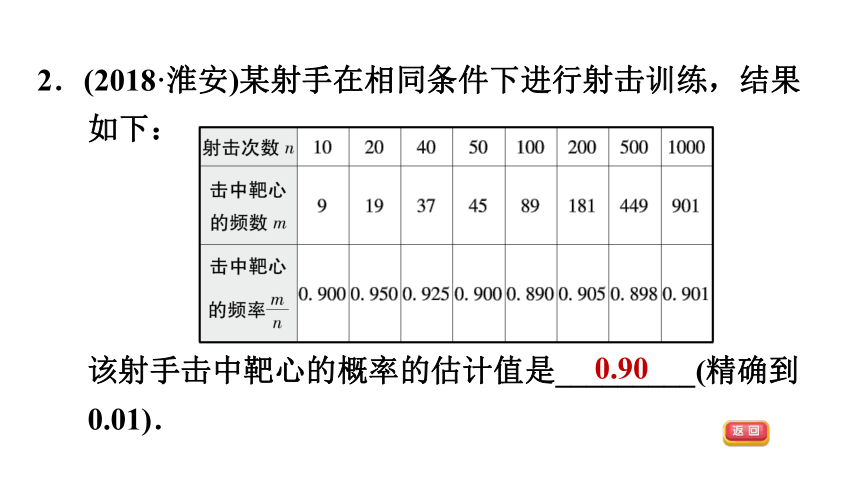
2.(2018·淮安)某射手在相同条件下进行射击训练,结果如下:
该射手击中靶心的概率的估计值是_________(精确到0.01).
0.90
3.(2017·兰州)一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20 B.24 C.28 D.30
D
4.(中考·南通)在一个不透明的盒子中装有a个除颜色外完全相同的球,这a个球中只有3个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值大约为( )
A.12 B.15 C.18 D.21
B
5.(中考·本溪)在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中.通过大量重复摸球试验发现,摸到黄球的频率是0.2,则估计口袋中大约有红球( )
A.16个 B.20个 C.25个 D.30个
A
6.在大量重复试验下,随机事件A发生的频率 (这里n是总试验次数,它必须相当大,m是在n次试验中事件A发生的次数)会稳定到某个常数p,于是我们用p表示事件A发生的概率,即P(A)=________.
p
7.(2018·锦州)如图,这是一幅长为3 m,宽为2 m的长方形世界杯宣传画,为测量宣传画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子
落在世界杯图案中的频率稳定在常数0.4附近,
由此可估计宣传画上世界杯图案的面积约为
________m2.
2.4
8.(中考·山西)在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
9.(2018·呼和浩特)某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的试验最有可能的是( )
A.袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B.掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C.先后两次掷一枚质地均匀的硬币,两次都出现反面
D.先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
D
10.(中考·宁夏)为了解学生的体能情况,随机选取了1 000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑,则该学生同时喜欢短跑、跳绳、跳远中哪项的可能性最大?
解:喜欢长跑的700名学生中,有150名学生喜欢短跑、550名学生喜欢跳绳、200名学生喜欢跳远,
所以喜欢长跑的学生又同时喜欢跳绳的可能性最大.
11.(2017·滨州)为了考察甲、乙两种成熟期小麦的株高长势情况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表:
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
甲 63 66 63 61 64 61
乙 63 65 60 63 64 63
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
整合方法·提升练
解:列表如下:
由表可知,共有36种等可能的结果,其中两株配对小麦株高恰好都等于各自平均株高的有6种,∴所抽取的两株配对小麦株高恰好都等于各自平均株高的概率为
? 63 66 63 61 64 61
63 63,63 66,63 63,63 61,63 64,63 61,63
65 63,65 66,65 63,65 61,65 64,65 61,65
60 63,60 66,60 63,60 61,60 64,60 61,60
63 63,63 66,63 63,63 61,63 64,63 61,63
64 63,64 66,64 63,64 61,64 64,64 61,64
63 63,63 66,63 63,63 61,63 64,63 61,63
12.(2018·自贡)某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:
(1)在这次调查中,一共调查了________名学生;
(2)补全条形统计图;
100
解:爱好上网的人数为100×10%=10,
则爱好阅读的人数为100-40-20-10=30.
补全条形统计图如图所示.
(3)若该校共有1 500名学生,估计爱好运动的学生有________名;
(4)在全校学生中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是________.
600
第2节 用频率估计概率
第三章 概率的进一步认识
北师版 九年级上
答案显示
习题链接
频率
0.90
D
B
A
2.4
D
D
p
答案显示
习题链接
1.求一个随机事件概率的基本方法可以是:通过大量的重复试验,用一个随机事件发生的________去估计它的概率.
概率
2.(2018·淮安)某射手在相同条件下进行射击训练,结果如下:
该射手击中靶心的概率的估计值是_________(精确到0.01).
0.90
3.(2017·兰州)一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20 B.24 C.28 D.30
D
4.(中考·南通)在一个不透明的盒子中装有a个除颜色外完全相同的球,这a个球中只有3个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值大约为( )
A.12 B.15 C.18 D.21
B
5.(中考·本溪)在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中.通过大量重复摸球试验发现,摸到黄球的频率是0.2,则估计口袋中大约有红球( )
A.16个 B.20个 C.25个 D.30个
A
6.在大量重复试验下,随机事件A发生的频率 (这里n是总试验次数,它必须相当大,m是在n次试验中事件A发生的次数)会稳定到某个常数p,于是我们用p表示事件A发生的概率,即P(A)=________.
p
7.(2018·锦州)如图,这是一幅长为3 m,宽为2 m的长方形世界杯宣传画,为测量宣传画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子
落在世界杯图案中的频率稳定在常数0.4附近,
由此可估计宣传画上世界杯图案的面积约为
________m2.
2.4
8.(中考·山西)在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
9.(2018·呼和浩特)某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的试验最有可能的是( )
A.袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B.掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C.先后两次掷一枚质地均匀的硬币,两次都出现反面
D.先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
D
10.(中考·宁夏)为了解学生的体能情况,随机选取了1 000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑,则该学生同时喜欢短跑、跳绳、跳远中哪项的可能性最大?
解:喜欢长跑的700名学生中,有150名学生喜欢短跑、550名学生喜欢跳绳、200名学生喜欢跳远,
所以喜欢长跑的学生又同时喜欢跳绳的可能性最大.
11.(2017·滨州)为了考察甲、乙两种成熟期小麦的株高长势情况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表:
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
甲 63 66 63 61 64 61
乙 63 65 60 63 64 63
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
整合方法·提升练
解:列表如下:
由表可知,共有36种等可能的结果,其中两株配对小麦株高恰好都等于各自平均株高的有6种,∴所抽取的两株配对小麦株高恰好都等于各自平均株高的概率为
? 63 66 63 61 64 61
63 63,63 66,63 63,63 61,63 64,63 61,63
65 63,65 66,65 63,65 61,65 64,65 61,65
60 63,60 66,60 63,60 61,60 64,60 61,60
63 63,63 66,63 63,63 61,63 64,63 61,63
64 63,64 66,64 63,64 61,64 64,64 61,64
63 63,63 66,63 63,63 61,63 64,63 61,63
12.(2018·自贡)某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:
(1)在这次调查中,一共调查了________名学生;
(2)补全条形统计图;
100
解:爱好上网的人数为100×10%=10,
则爱好阅读的人数为100-40-20-10=30.
补全条形统计图如图所示.
(3)若该校共有1 500名学生,估计爱好运动的学生有________名;
(4)在全校学生中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是________.
600
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
