高中数学人教A版选修1-1第二章 圆锥曲线与方程2.3 抛物线(共24张PPT)
文档属性
| 名称 | 高中数学人教A版选修1-1第二章 圆锥曲线与方程2.3 抛物线(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 630.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 21:31:57 | ||
图片预览




文档简介
(共24张PPT)
抛物线及其标准方程(一)
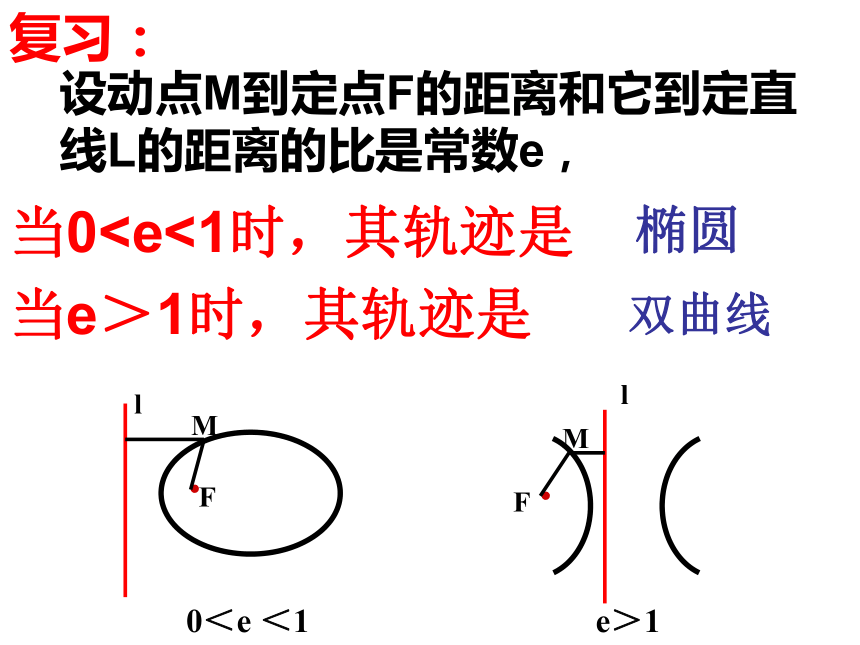
当e>1时,其轨迹是
复习:
椭圆
双曲线
设动点M到定点F的距离和它到定直线L的距离的比是常数e,
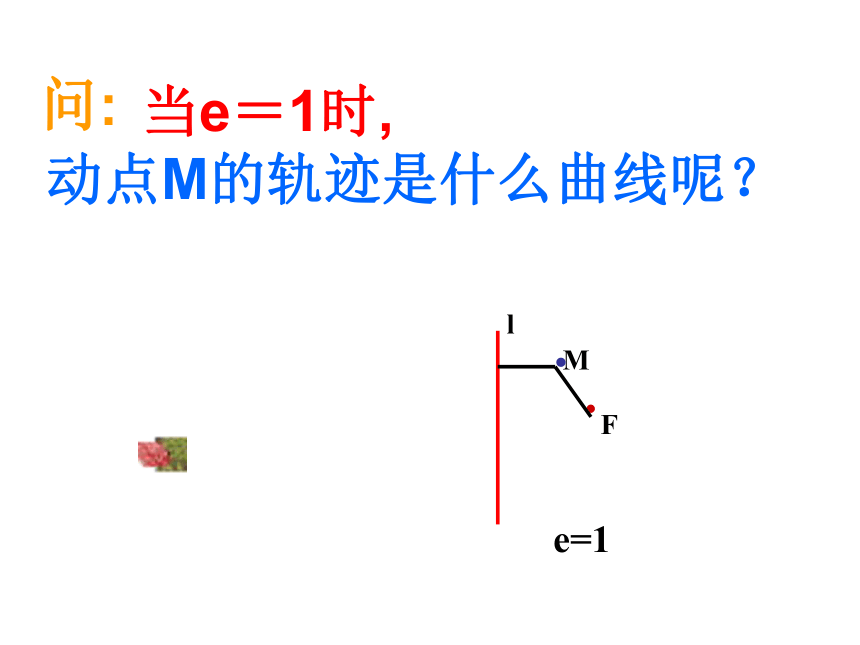
当0问:
当e=1时, 动点M的轨迹是什么曲线呢?
新授:
一、定义
平面内与一个定点F和一条定直线L
的距离相等的点的轨迹叫做抛物线
定点F叫做抛物线的
焦点
定直线L 叫做抛物线的
准线
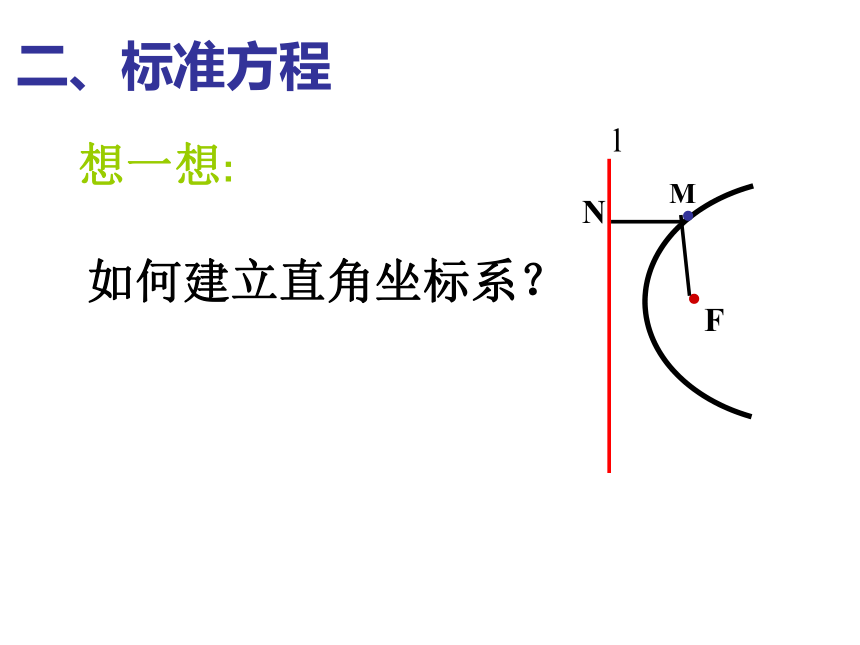
二、标准方程
如何建立直角坐标系?
想一想:
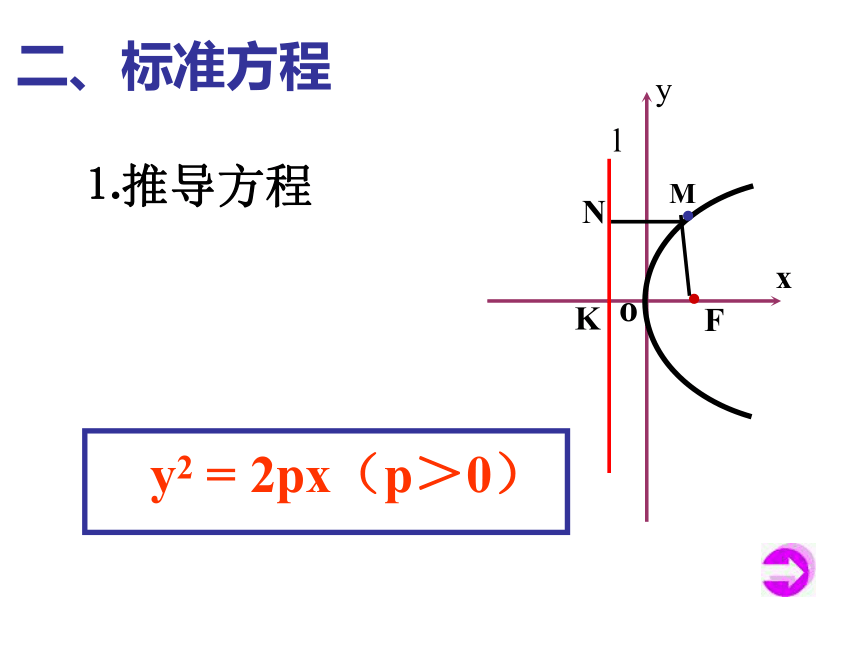
二、标准方程
K
⒈推导方程
方程 y2 = 2px(p>0)叫做
抛物线的标准方程。
其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离
它表示抛物线的焦点在 x轴的右半轴 上.
图 形 焦 点 准 线 标准方程
说明:
1、如果定点正好在定直线上,
点M的轨迹还是抛物线吗?
2、p的大小与抛物线的
形状的关系
3、根据抛物线标准方程的形式,
如何判断抛物线的焦点位置,
开口方向?
(1)已知抛物线的标准方程
是y2 = 6x,
求它的焦点坐标和准线方程;
例1:
(2)已知抛物线的方程是
y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。
例2:求过点A(-3,2)的抛物线的
标准方程。
例3:已知点M与点F(4,0)的距离
比它到直线L:x+5=0的距离小1,
求点M的轨迹方程。
例4、(1)M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是
————————————
(2) 抛物线y2=12x上与焦点的距
离等于9的点的坐标是_________.
小 结 :
1、基本知识:抛物线的定义、四种标准方程形式及其对应关系。
2、思想方法:注重数形结合。
1.抛物线标准方程与二次函数
之间有什么区别与联系?
2.抛物线标准方程与椭圆、双曲
线的标准方程有什么区别与联系?
练习
1、根据下列条件,
写出抛物线的标准方程:
(1)焦点是F(3,0);
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y
(5,0)
x= -5
(0,-2)
y=2
go
焦点坐标 准线方程
1)
2)
3)
4)
课外作业:P64 2,3
抛物线及其标准方程(一)
当e>1时,其轨迹是
复习:
椭圆
双曲线
设动点M到定点F的距离和它到定直线L的距离的比是常数e,
当0
当e=1时, 动点M的轨迹是什么曲线呢?
新授:
一、定义
平面内与一个定点F和一条定直线L
的距离相等的点的轨迹叫做抛物线
定点F叫做抛物线的
焦点
定直线L 叫做抛物线的
准线
二、标准方程
如何建立直角坐标系?
想一想:
二、标准方程
K
⒈推导方程
方程 y2 = 2px(p>0)叫做
抛物线的标准方程。
其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离
它表示抛物线的焦点在 x轴的右半轴 上.
图 形 焦 点 准 线 标准方程
说明:
1、如果定点正好在定直线上,
点M的轨迹还是抛物线吗?
2、p的大小与抛物线的
形状的关系
3、根据抛物线标准方程的形式,
如何判断抛物线的焦点位置,
开口方向?
(1)已知抛物线的标准方程
是y2 = 6x,
求它的焦点坐标和准线方程;
例1:
(2)已知抛物线的方程是
y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。
例2:求过点A(-3,2)的抛物线的
标准方程。
例3:已知点M与点F(4,0)的距离
比它到直线L:x+5=0的距离小1,
求点M的轨迹方程。
例4、(1)M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是
————————————
(2) 抛物线y2=12x上与焦点的距
离等于9的点的坐标是_________.
小 结 :
1、基本知识:抛物线的定义、四种标准方程形式及其对应关系。
2、思想方法:注重数形结合。
1.抛物线标准方程与二次函数
之间有什么区别与联系?
2.抛物线标准方程与椭圆、双曲
线的标准方程有什么区别与联系?
练习
1、根据下列条件,
写出抛物线的标准方程:
(1)焦点是F(3,0);
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y
(5,0)
x= -5
(0,-2)
y=2
go
焦点坐标 准线方程
1)
2)
3)
4)
课外作业:P64 2,3
