苏科版八年级下册数学:9.4 正方形中的最值问题 专题训练课件(共16张PPT)
文档属性
| 名称 | 苏科版八年级下册数学:9.4 正方形中的最值问题 专题训练课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 18:47:22 | ||
图片预览



文档简介
(共16张PPT)
知识点回顾
基本图形解析:
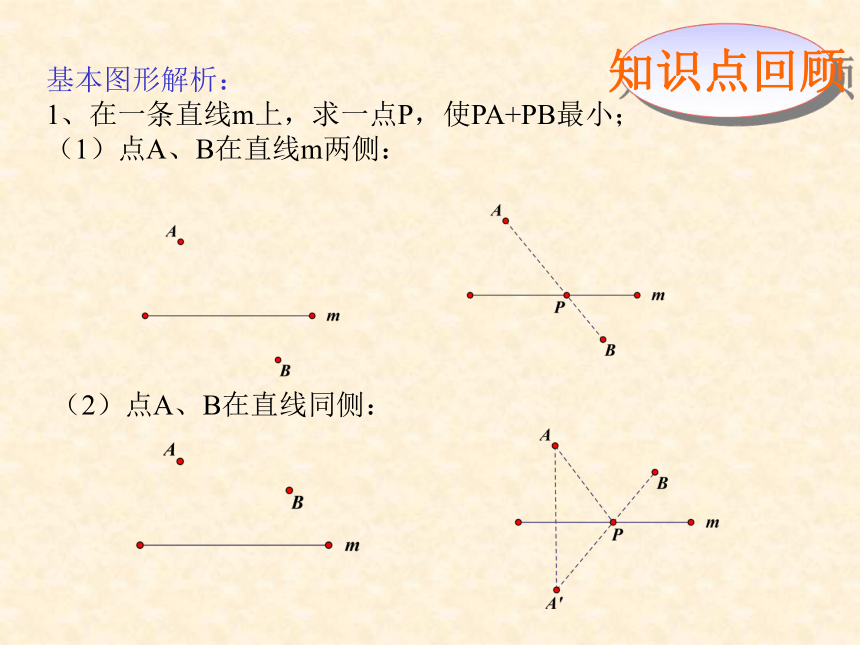
1、在一条直线m上,求一点P,使PA+PB最小;
(1)点A、B在直线m两侧:
(2)点A、B在直线同侧:
知识点回顾
基本图形解析:
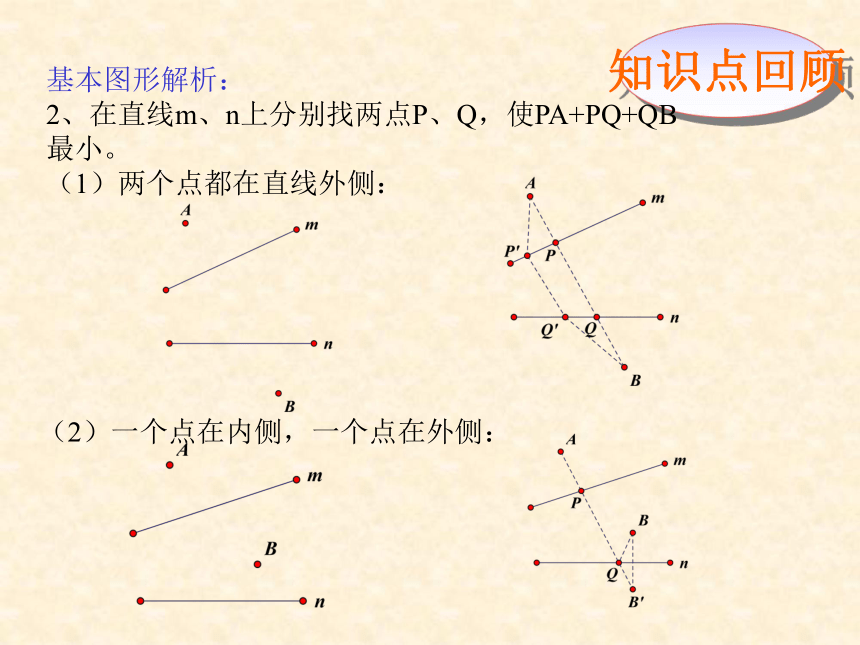
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(1)两个点都在直线外侧:
(2)一个点在内侧,一个点在外侧:
知识点回顾
基本图形解析:
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(3)两个点都在内侧:
知识点回顾
基本图形解析:
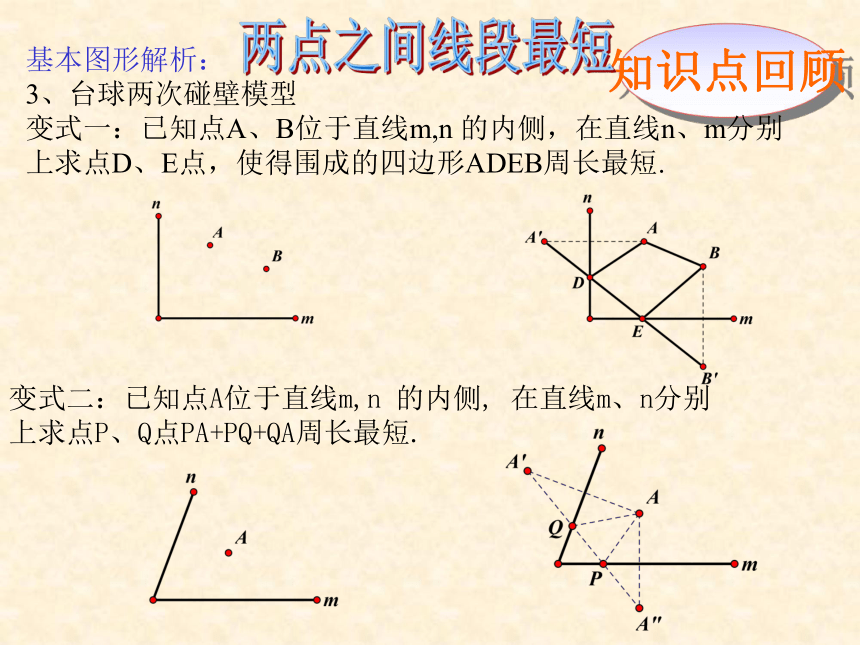
3、台球两次碰壁模型
变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.
变式二:已知点A位于直线m,n 的内侧, 在直线m、n分别
上求点P、Q点PA+PQ+QA周长最短.
知识点回顾
基本图形解析:
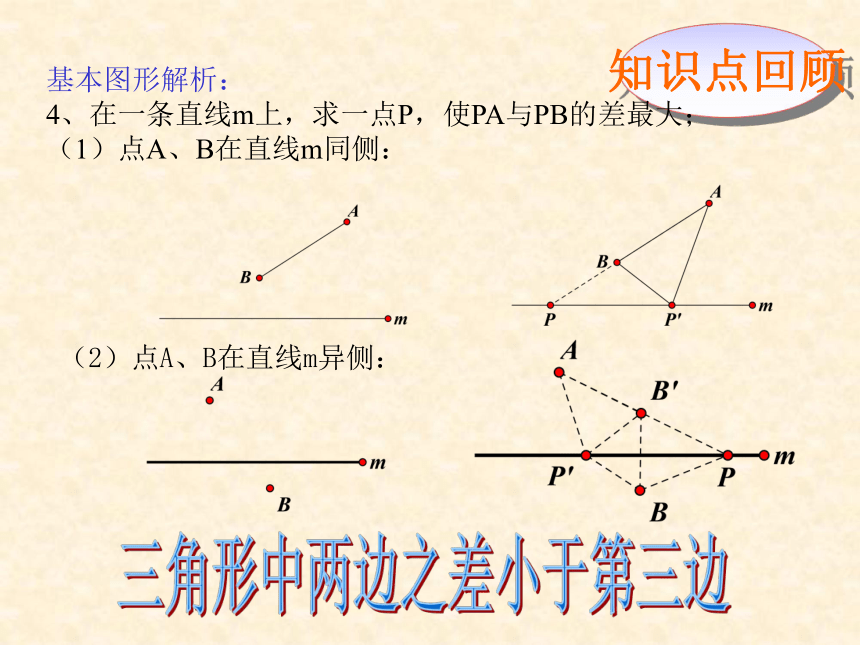
4、在一条直线m上,求一点P,使PA与PB的差最大;
(1)点A、B在直线m同侧:
(2)点A、B在直线m异侧:
知识点回顾
其它非基本图形类线段和差最值问题
1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
2、在转化较难进行时需要借助于三角形的中位线及直角三角形斜边上的中线。
3、线段之和的问题往往是将各条线段串联起来,再连接首尾端点,根据两点之间线段最短以及点到线的距离垂线段最短的基本依据解决。
4、点到圆的距离相关知识点。
例1. 如图,正方形ABCD中,AB=4,E是BC的中点,点P是对角线AC上一动点,则PE+PB的最小值为 .
两点之间线段最短(对称点已知)
习题讲解
解析:PE+PB的最小值即线段DE的长,用勾股定理求出DE长。
P
练
习
题
1.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 ( )
【解析】设BE与AC交于点P',连接BD,P'D.∵点B与D关于AC对称,
∴P'D=P'B,∴P'D+P'E=P'B+P'E=BE,当点P位于点P'处时,PD+PE
最小.∵正方形ABCD的面积为16,∴AB=4,又∵△ABE是等边三角
形,∴BE=AB=4,∴PD+PE的最小值为4.
C
P
例2.如图,∠MON=90?,矩形ABCD的顶点B、C分别在边OM、ON上,当B在边OM上运动时,C随之在边ON上运动,若CD=5,BC=24,运动过程中,点D到点O的最大距离为 .
习题讲解
25
2.如图,平面直角坐标系中,点A、B分别
是x、y轴上的动点,以AB为边作边长
为2的正方形ABCD,则OC的最大值为 .
练
习
题
例3.如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是 .
习题讲解
B’
2√10-2
3.如图,在 中, ,点P为BC上任意一点,连接PA,以PAPC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
练
习
题
例4.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是______.
习题讲解
P
H
例5. 如图,正方形ABCD与矩形EFGH在直线L的同侧,边AD、EH在直线L上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线L左右移动,连接BF、CG,则BF+CG的最小值为 cm.
习题讲解
知识点回顾
基本图形解析:
1、在一条直线m上,求一点P,使PA+PB最小;
(1)点A、B在直线m两侧:
(2)点A、B在直线同侧:
知识点回顾
基本图形解析:
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(1)两个点都在直线外侧:
(2)一个点在内侧,一个点在外侧:
知识点回顾
基本图形解析:
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(3)两个点都在内侧:
知识点回顾
基本图形解析:
3、台球两次碰壁模型
变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.
变式二:已知点A位于直线m,n 的内侧, 在直线m、n分别
上求点P、Q点PA+PQ+QA周长最短.
知识点回顾
基本图形解析:
4、在一条直线m上,求一点P,使PA与PB的差最大;
(1)点A、B在直线m同侧:
(2)点A、B在直线m异侧:
知识点回顾
其它非基本图形类线段和差最值问题
1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
2、在转化较难进行时需要借助于三角形的中位线及直角三角形斜边上的中线。
3、线段之和的问题往往是将各条线段串联起来,再连接首尾端点,根据两点之间线段最短以及点到线的距离垂线段最短的基本依据解决。
4、点到圆的距离相关知识点。
例1. 如图,正方形ABCD中,AB=4,E是BC的中点,点P是对角线AC上一动点,则PE+PB的最小值为 .
两点之间线段最短(对称点已知)
习题讲解
解析:PE+PB的最小值即线段DE的长,用勾股定理求出DE长。
P
练
习
题
1.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 ( )
【解析】设BE与AC交于点P',连接BD,P'D.∵点B与D关于AC对称,
∴P'D=P'B,∴P'D+P'E=P'B+P'E=BE,当点P位于点P'处时,PD+PE
最小.∵正方形ABCD的面积为16,∴AB=4,又∵△ABE是等边三角
形,∴BE=AB=4,∴PD+PE的最小值为4.
C
P
例2.如图,∠MON=90?,矩形ABCD的顶点B、C分别在边OM、ON上,当B在边OM上运动时,C随之在边ON上运动,若CD=5,BC=24,运动过程中,点D到点O的最大距离为 .
习题讲解
25
2.如图,平面直角坐标系中,点A、B分别
是x、y轴上的动点,以AB为边作边长
为2的正方形ABCD,则OC的最大值为 .
练
习
题
例3.如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是 .
习题讲解
B’
2√10-2
3.如图,在 中, ,点P为BC上任意一点,连接PA,以PAPC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
练
习
题
例4.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是______.
习题讲解
P
H
例5. 如图,正方形ABCD与矩形EFGH在直线L的同侧,边AD、EH在直线L上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线L左右移动,连接BF、CG,则BF+CG的最小值为 cm.
习题讲解
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
