沪科版数学七年级下册10.3平行线的性质课件 (共16张PPT)
文档属性
| 名称 | 沪科版数学七年级下册10.3平行线的性质课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 205.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 00:00:00 | ||
图片预览



文档简介
课件16张PPT。10.3平行线的性质忆一忆你还记得判定两直线平行的方法有哪些吗?
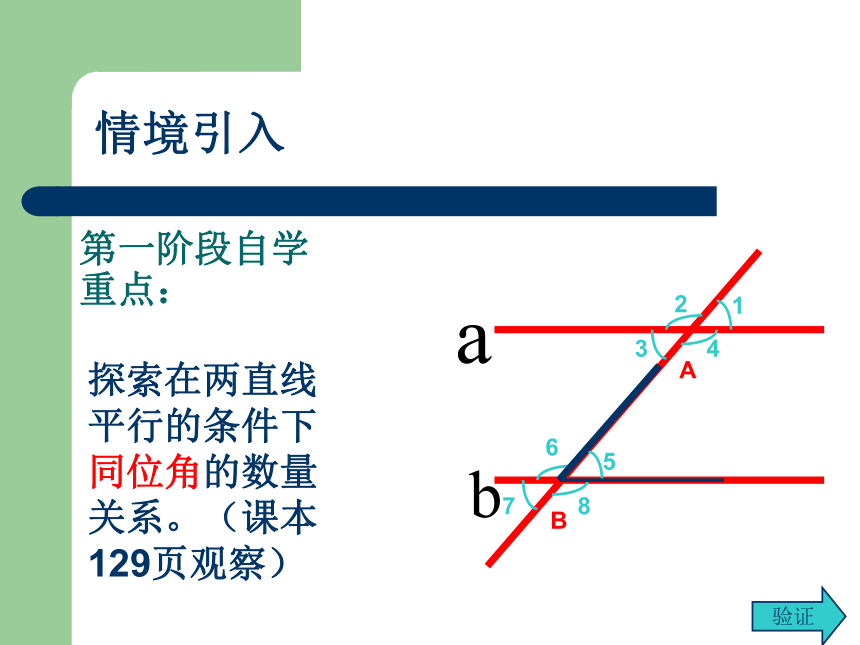
同位角相等, 两直线平行。内错角相等, 两直线平行。同旁内角互补,两直线平行。两直线平行?角的数量关系两直线位置关系角的数量关系反过来:第一阶段自学重点:探索在两直线平行的条件下同位角的数量关系。(课本129页观察)情境引入验证两条平行线被第三条直线所截,同位角相等。性质解析:简称:两直线平行,同位角相等判断: 1、同位角都相等( )
2、两直线被第三条直线所截,
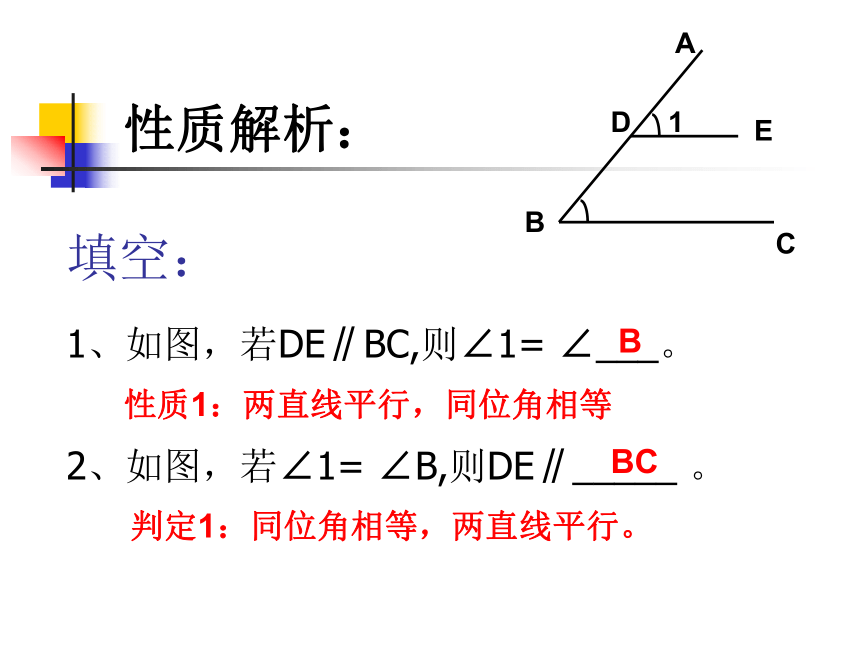
同位角相等。( )××平行线的性质1:填空:1、如图,若DE∥BC,则∠1= ∠___。
ABDE2、如图,若∠1= ∠B,则DE∥_____ 。
性质1:两直线平行,同位角相等判定1:同位角相等,两直线平行。BBC性质解析:第二阶段自学重点:在性质1的基础上,探索在两直线平行的条件下内错角及同旁内角的数量关系。
并用两种语言正确描述你所得结论。
从中体会性质的应用和简单逻辑推理的符号表达。
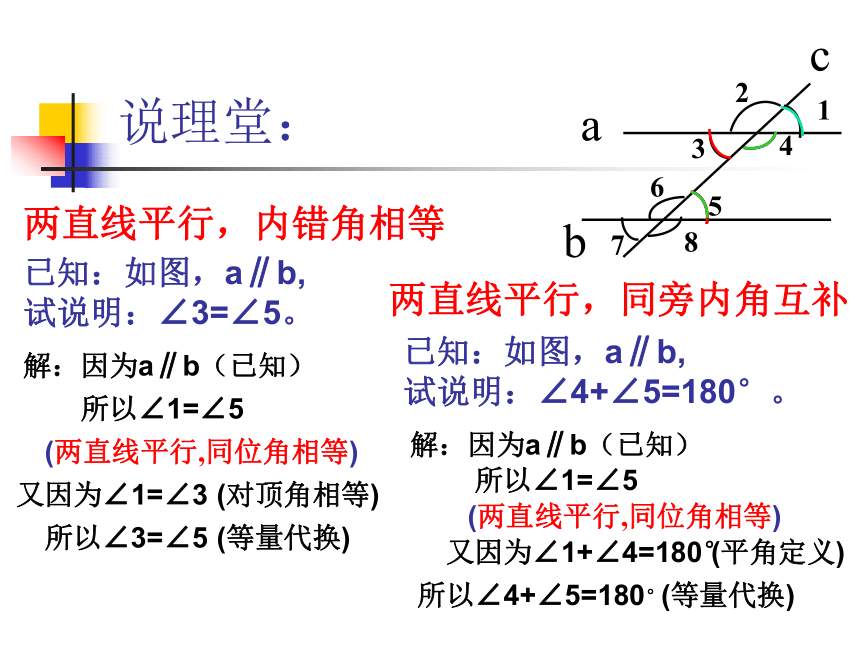
描述应用符号表达两种语言学习内容:课本第129页至130页内容内错角同旁内角说理堂:两直线平行,内错角相等两直线平行,同旁内角互补已知:如图,a∥b,试说明:∠3=∠5。 解:因为a∥b(已知)所以∠1=∠5(两直线平行,同位角相等)又因为∠1=∠3(对顶角相等)所以∠3=∠5(等量代换)已知:如图,a∥b,
试说明:∠4+∠5=180°。 解:因为a∥b(已知)所以∠1=∠5(两直线平行,同位角相等)又因为∠1+∠4=180°(平角定义)所以∠4+∠5=180°(等量代换)性质解析:1.内错角都相等( )
2.同旁内角都互补。( )××两条平行线被第三条直线所截,内错角相等。平行线的性质2:两条平行线被第三条直线所截,同旁内角互补。平行线的性质3:简称:两直线平行,内错角相等简称:两直线平行,同旁内角互补判断: 填空:如图,
1、若DE∥BC,则∠3= ∠___
依据:_________________ABCDE13、若∠3= ∠2,则__∥___
依据:__________________
4、若∠2+ ∠4=180°,则__ ∥__
依据:__________________。性
质判
定DE BCF22、若DE∥BC,则∠2+ ∠__=180°
依据:__________________4两直线平行,内错角相等两直线平行,同旁内角互补内错角相等,两直线平行DE BC同旁内角互补,两直线平行性质解析:平行线的判定同位角相等, 两直线平行.内错角相等, 两直线平行.同旁内角互补,两直线平行.平行线的性质两直线平行, 同位角相等.两直线平行, 内错角相等.两直线平行,同旁内角互补.比较角的关系两直线平行两直线平行角的关系例题解析如图所示,已知点D、E、F分别在△ABC的边AB,AC,BC上,且DE∥BC,∠C=58°
1、试求∠AED的度数;
2、如果∠EDF=58 °,
那么DF与AC平行吗?小结6558 °58 °58 °小试牛刀 如图,在四边形ABCD中,AB∥DC , AD∥BC,∠A=71°试求∠C的度数。解:因为 AD//BC (已知)所以∠A+∠B=180°(两直线平行,同旁内角互补)所以 ∠C+∠B=180°因为 ∠A=71° (已知)(同角的补角相等)因为 AB//DC (已知)(两直线平行,同旁内角互补)所以 ∠C=∠A所以 ∠C=∠A=71°(等量代换)课堂小结谈谈你在这节课学习中的收获角的关系两直线平行两直线平行角的关系1、平行线的判定平行线的性质2、平行线的性质1 转化 性质2 转化 性质3 转化 转化的关键就是找到过渡角作业布置课本习题10.3第3题和第4题1 如图, 已知AG//CF,
∠A=∠C ,
试说明AB//CD.
变式再练作业大胆尝试:如图,已知D是AB上的一点,E是AC上的一点,∠ADE=60°,∠B=60°,∠AED=40°
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?作业
同位角相等, 两直线平行。内错角相等, 两直线平行。同旁内角互补,两直线平行。两直线平行?角的数量关系两直线位置关系角的数量关系反过来:第一阶段自学重点:探索在两直线平行的条件下同位角的数量关系。(课本129页观察)情境引入验证两条平行线被第三条直线所截,同位角相等。性质解析:简称:两直线平行,同位角相等判断: 1、同位角都相等( )
2、两直线被第三条直线所截,
同位角相等。( )××平行线的性质1:填空:1、如图,若DE∥BC,则∠1= ∠___。
ABDE2、如图,若∠1= ∠B,则DE∥_____ 。
性质1:两直线平行,同位角相等判定1:同位角相等,两直线平行。BBC性质解析:第二阶段自学重点:在性质1的基础上,探索在两直线平行的条件下内错角及同旁内角的数量关系。
并用两种语言正确描述你所得结论。
从中体会性质的应用和简单逻辑推理的符号表达。
描述应用符号表达两种语言学习内容:课本第129页至130页内容内错角同旁内角说理堂:两直线平行,内错角相等两直线平行,同旁内角互补已知:如图,a∥b,试说明:∠3=∠5。 解:因为a∥b(已知)所以∠1=∠5(两直线平行,同位角相等)又因为∠1=∠3(对顶角相等)所以∠3=∠5(等量代换)已知:如图,a∥b,
试说明:∠4+∠5=180°。 解:因为a∥b(已知)所以∠1=∠5(两直线平行,同位角相等)又因为∠1+∠4=180°(平角定义)所以∠4+∠5=180°(等量代换)性质解析:1.内错角都相等( )
2.同旁内角都互补。( )××两条平行线被第三条直线所截,内错角相等。平行线的性质2:两条平行线被第三条直线所截,同旁内角互补。平行线的性质3:简称:两直线平行,内错角相等简称:两直线平行,同旁内角互补判断: 填空:如图,
1、若DE∥BC,则∠3= ∠___
依据:_________________ABCDE13、若∠3= ∠2,则__∥___
依据:__________________
4、若∠2+ ∠4=180°,则__ ∥__
依据:__________________。性
质判
定DE BCF22、若DE∥BC,则∠2+ ∠__=180°
依据:__________________4两直线平行,内错角相等两直线平行,同旁内角互补内错角相等,两直线平行DE BC同旁内角互补,两直线平行性质解析:平行线的判定同位角相等, 两直线平行.内错角相等, 两直线平行.同旁内角互补,两直线平行.平行线的性质两直线平行, 同位角相等.两直线平行, 内错角相等.两直线平行,同旁内角互补.比较角的关系两直线平行两直线平行角的关系例题解析如图所示,已知点D、E、F分别在△ABC的边AB,AC,BC上,且DE∥BC,∠C=58°
1、试求∠AED的度数;
2、如果∠EDF=58 °,
那么DF与AC平行吗?小结6558 °58 °58 °小试牛刀 如图,在四边形ABCD中,AB∥DC , AD∥BC,∠A=71°试求∠C的度数。解:因为 AD//BC (已知)所以∠A+∠B=180°(两直线平行,同旁内角互补)所以 ∠C+∠B=180°因为 ∠A=71° (已知)(同角的补角相等)因为 AB//DC (已知)(两直线平行,同旁内角互补)所以 ∠C=∠A所以 ∠C=∠A=71°(等量代换)课堂小结谈谈你在这节课学习中的收获角的关系两直线平行两直线平行角的关系1、平行线的判定平行线的性质2、平行线的性质1 转化 性质2 转化 性质3 转化 转化的关键就是找到过渡角作业布置课本习题10.3第3题和第4题1 如图, 已知AG//CF,
∠A=∠C ,
试说明AB//CD.
变式再练作业大胆尝试:如图,已知D是AB上的一点,E是AC上的一点,∠ADE=60°,∠B=60°,∠AED=40°
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?作业
